锥阀阀口能量损失分析及阀座结构改进

杨国来,张灿罡,尹大禹,张东东,王建忠

(1.兰州理工大学 能源与动力工程学院,甘肃 兰州 730050;2.兰州理工大学 温州泵阀工程研究院,浙江 温州 325105)



锥阀阀口能量损失分析及阀座结构改进

杨国来1,2,张灿罡1,2,尹大禹1,2,张东东1,2,王建忠1,2

(1.兰州理工大学 能源与动力工程学院,甘肃 兰州 730050;2.兰州理工大学 温州泵阀工程研究院,浙江 温州 325105)

通过对锥阀在不同锥角、不同阀口开度及不同压差条件下的速度场和压力场进行分析,类比电路基本理论,得到了在不同压差条件下压力及速度梯度变化的规律,并分析了锥阀阀口的能量损失规律;与此同时分析锥阀阀口涡流产生的原因,通过对阀座结构进行改进,以减少涡流大小,从而达到降低能量损失的目的,为锥阀的设计提供了理论参考依据。

锥角;压差;涡流;能量损失

锥阀是液压系统中常被用的元件之一,常被用作压力控制阀的主阀或者导阀,工作时因其阀口开度较小,高压液压油流经节流口时,过流面积收缩,流速变快,随之而来会产生气穴以及啸叫现象,从而使得阀的噪声很大,并伴随阀的发热,能量损失过多。针对此种现象,分析了锥阀在不同锥角、不同阀口开度、不同压差条件下的压力及速度变化规律及涡流产生的原因,并对锥阀座的形状进行了改进,以减少涡流造成的能量损失,减小阀的噪声。这对于认识阀口流动状态,优化阀芯和阀座结构,延长阀的寿命具有重要意义。

高殿荣等[1]对液压锥阀进行了有限元分析,并对阀芯进行了改进,对锥阀流道优化设计具有指导意义。冀宏等[2]通过在阀芯上开环形槽来改变阀口后的流道形状,进而改变阀后气穴区位置,减小气穴噪声。高红等[3]对锥阀阀口进行了流场可视化研究,获得了阀口的气穴分布模型。

上述研究主要针对锥阀的气穴、气蚀现象,而对于锥阀设计中要考虑的因素及能量损失的研究同样具有重要的意义。研究着重从工程角度出发,对不同工况下流场进行分析,类比电路基本定律,对压降分布进行了分析,研究了减少锥阀能量损失的方法。

1 CFD计算模型

1.1 流体基本方程

流体在运动过程中遵守物理守恒定律。当流体运动状态为湍流时,根据计算流体动力学(CFD,computationalfluiddynamics)流体基本方程以及附加湍流输运方程,对流体的运动过程进行计算。

对应的流体控制方程如下:

(1)质量守恒方程为

其中:ρ为流体密度;ui为i方向速度。

(2)动量守恒方程为

其中:uj为j方向速度;p为静压;τij为应力张量;ρgi为重力体积力;Fi为外部体积力。

(3)能量守恒方程为[4]

其中:keff为有效导热系数;Jj′为组分j′的扩散通量;Sh为包括化学反应热和其他体积热源的源项;hj′为组分j′的焓。

该方程右边三项分别为导热项、组分扩散项、粘性耗散项。

1.2 网格划分与计算模型

由于锥阀的结构尺寸较小,为尽可能模拟真实情况下阀口的流动状况,减少计算量,将锥阀流场模型简化为二维轴对称模型。分别建立不同锥角(锥角分别为45°、60°、75°)下的二维轴对称锥阀模型(见图1)。划分结构化网格,为了精确反应阀口附近的流场情况,对阀口处进行了网格细化。

图1 二维轴对称结构化网格模型Fig.1 Two-dimension axial symmetry structured grid model

计算边界条件为:阀芯左右两端分别为出口和进口,设定为压力出口和压力进口,流体与壁面接触的边界为静止壁面。由于该模拟的雷诺数Re>2 000,数值计算采用标准κ-ε湍流模型,用有限体积法中常用的SIMPLE算法,求解离散方程组用FirstOrderUpwind来耦合压力梯度,按照定常流动进行计算。油液密度为900kg/m3,动力粘度为0.04Pa·s。

2 计算结果及分析

2.1 不同锥角下锥阀的性能

液流在流经锥阀阀口前后可以抽象为先是突缩管再是突扩管,突缩和突扩的过程中,若是突扩角和突缩角选取的不合适,会增大流体噪声和能量损失。对于锥阀而言,突扩角和突缩角的确定本质是对锥阀锥角的研究,因为锥角直接决定了突缩角和突扩角的大小。

(1)不同锥角下速度云图 在保证锥阀进出口压差相同的情况下,对不同锥角锥阀进行仿真,得到如图2所示的速度云图。

图2 不同锥角下速度云图Fig.2 Velocity nephogram with different cone angle

比较在相同压差,不同锥角下的速度云图。由图2可以看出,随着锥角的增大,速度梯度较大的集中区域在减小,45°锥角时最大的速度梯度基本集中于阀口过流面积之后,60°锥角时也主要集中在阀口后部,且速度集中区域在减小,75°锥角时,绝大部分集中在阀口过流面积处,且速度梯度较大的集中区域很小。

(2)不同锥角下压力云图 在保证锥阀进出口相同压差的条件下,对不同锥角锥阀进行仿真,得到如图3所示的压力云图。

比较在相同压差,不同锥角下的压力云图。由图3可以看出,随着锥角增大,阀口处压力分布变得越来越集中。

综上可知,增大锥阀的锥角,可以减少阀口过流面积处速度集中区域面积大小,使得噪声减小。但是随着锥角的增大,阀口处压力分布变得越来越集中,阀口处总的压力损失在加大。

图3 不同锥角下压力云图Fig.3 Pressure nephogram with different cone angle

在本例中,阀口过流面积的计算公式为[5]

A=πdxsinα,

其中:d为阀座孔直径;x为阀芯升高量;α为锥阀半锥角。由此公式可知,阀芯升高量变化与半锥角变化导致的阀口过流面积的变化趋势一致。随着阀芯升高量的增加,锥阀阀口开度的大小也随之增加,故而可知阀口增大时,阀口速度和压力变化趋势与锥角增大时一致。对不同开度下阀口进行流场仿真,推断得到证实,这里不再列举不同阀口开度下的速度云图和压力云图[6-8]。

2.2 不同压差下锥阀的性能

(1)不同压差下速度曲线 在锥角相同的条件下,对不同压差下的锥阀进行仿真,得到如图4所示的速度云图。

图4 不同压差下速度云图Fig.4 Velocity nephogram with different differential pressure

比较相同阀口及锥角,不同压差下的锥阀压力分布。由图4可知,压差越大导致的速度梯度越大。

(2)不同压差下压力曲线 不同压差下的压力云图见图5。

图5 不同压差下的压力云图Fig.5 Pressure nephogram with different differential pressure

由图5可知,压差越大,压力分布就会越不集中,在阀口处压差变的集中,因此阀口处损失的能量在加大。类比电学欧姆定律,在电阻一定的情况下,压差越大,电流越大。如果将整个流道抽象成无数个电阻串联而成,如图6所示,阀口液流收缩处就是最大液阻处。

图6 液阻等效图Fig.6 Fluidic resistor equivalent diagram

3 锥阀阀座结构改进及涡流成因

对75°锥角,0.8mm阀口开度下阀流道进行流场分析,观察速度矢量。可以看出,由于阀座转弯为直角转弯,导致液流流过阀口时产生了涡流。鉴于此种状况,对阀座结构进行改进,阀口液流收缩处倒0.5°圆角,并且使整条边倾斜15°,改进前后的流道如图7所示。

流道改进前速度流线和流道改进后速度流线如图8所示。由图8可以看出,与改进之前的相比,改进之后的涡流明显减小,只在固体壁面周围存在一定的逆流,能量损失大大减少。分析涡流的成因,主要是因为在拐角处出现了流动的分离,拐角后面的油液被动的被主流所带动而旋转,产生涡流,能量被损失掉,同时增加流体的噪声。因此建议在设计加工阀座之初,根据加工条件,在阀座孔上设计适当大小的倒角,从根源上减小涡流的产生概率。

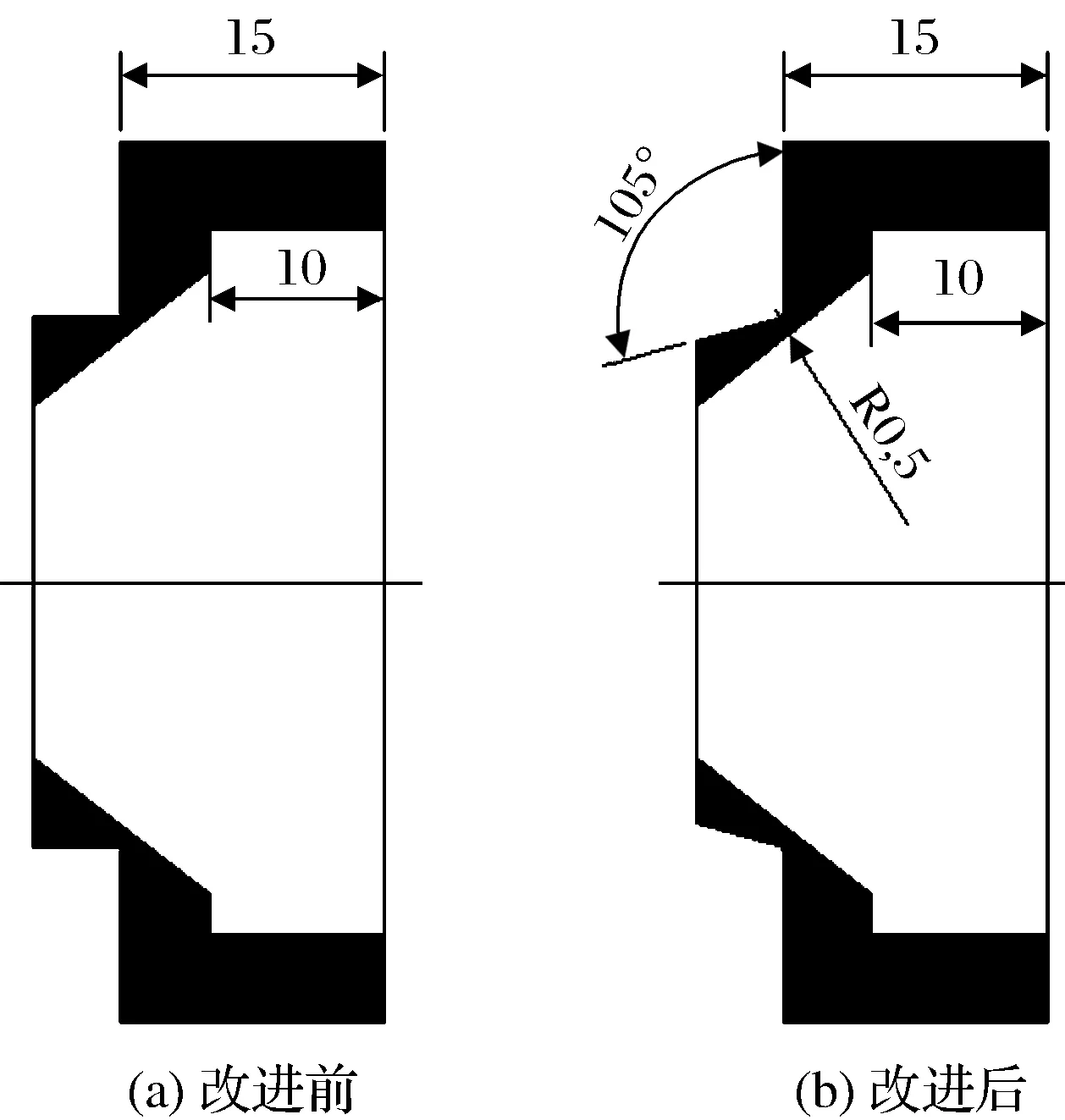
图7 改进前和改进后的流道Fig.7 Flow pass before and after improvement

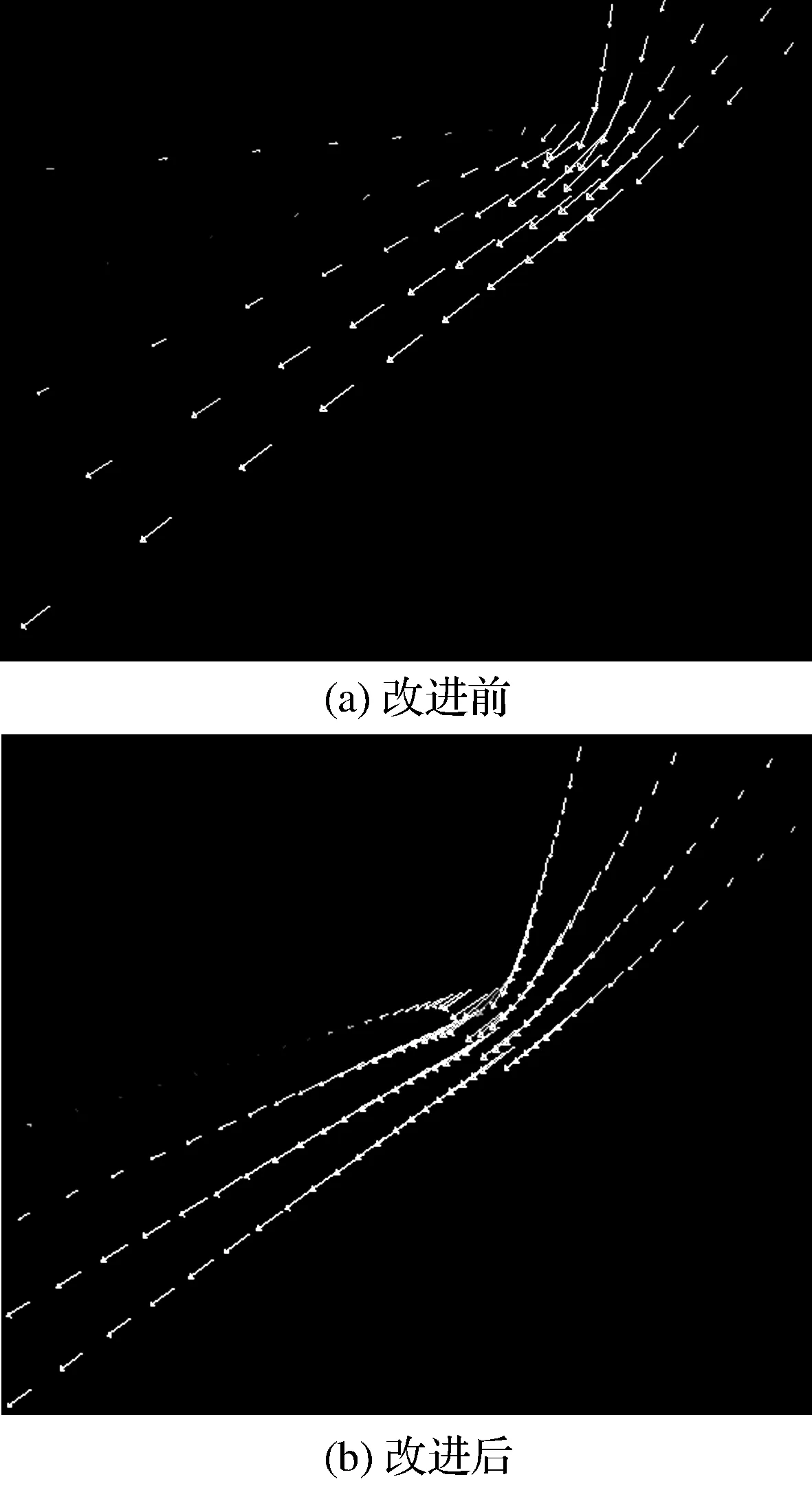
图8 改进前和改进后的速度流线Fig.8 Velocity flow pattern before and after improvement

4 结论

对不同锥角、不同阀口开度、不同压差下的锥阀

速度和压力云图进行分析,得到如下结论:增大锥阀的锥角,可以减少阀口过流面积处速度集中区域面积大小,使噪声减小,但是随着锥角的增大,阀口处压力变的越来越集中,阀口处总的压力能量损失在加大;阀口开度大小的变化的影响基本与锥角变化一致,本质上都是通过控制阀口开度大小达到控制阀的目的,最终实现压力、流量或者速度的控制;类比电学欧姆定律,压差越大,压力的分布变得越来越不集中,在阀口处压差变的集中,阀口处损失的能量在加大。

通过类比电学欧姆定律,可以帮助人们认识液压阀控制的本质,总结不同锥角、不同压差以及过流面积下阀工作状况,对阀的设计有很深的意义。最后对75°锥角、0.8mm开度时阀的流道进行了改进,改进后阀的密封性变得稍微差了一些,但是涡流尺度明显减小,能量损失大大减小,改进效果利大于弊。

[1] 高殿荣,王益群.液压锥阀流场的有限元法分析[J].机床与液压,2000,28(2):12-16.

[2] 冀宏,傅新,杨华勇.内流道开关对溢流阀气穴噪声影响的研究[J].机械工程学报,2002,38(8):19-22.

[3] 高红,傅新,杨华勇,等.锥阀阀口气穴流场的数值模拟与实验研究[J].机械工程学报,2002,38(8):27-30.

[4] 盛敬超.液压流体力学[M].北京:机械工业出版社,1975.

[5] 何存兴.液压元件[M].北京:机械工业出版社,1988.

[6] 张学静,李德明.多级导叶式离心泵导叶内部CFD计算分析[J].甘肃科学学报,2006,18(3):47-49.

[7] 杨瑞,李仁年,张士昂,等.水平轴风力机CFD计算湍流模型研究[J].甘肃科学学报,2008,20(4):90-93.

[8] 孙东宁,刘新强,王金林,等.一体化电动液压动力单元内气泡分布及气泡分离方法的研究[J].甘肃科学学报,2015,27(2):88-92.

ConeValvePortEnergyLossAnalysisandValveSeatStructureImprovement

YangGuolai1,2,ZhangCangang1,2,YinDayu1,2,ZhangDongdong1,2,WangJianzhong1,2

(1.SchoolofEnergyandPowerEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China; 2.WenzhouAcademyofPump&ValveEngineering,LanzhouUniversityofTechnology,Wenzhou325105,China)

Byanalyzingvelocityfieldandpressurefieldofconevalveindifferenttaperangle,valveportopeninganddifferentialpressureandbyanalogyofcircuitbasictheory,thepressureandvelocitychangingruleindifferentpressurecanbeachieved,analyzingenergylossruleofconevalve;meanwhile,analyzethecausethatthereiseddyinconevalveport,whichisasthebasetoimprovevalveseatstructureandreduceeddyforthepurposeofreducingtheenergylossandprovidingtheoryreferenceforgonevalvedesign.

Coneangle;Differentialpressure;Eddy;Energyloss

YangGuolai,ZhangCangang,YinDayu,etal.ConeValvePortEnergyLossAnalysisandValveSeatStructureImprovement[J].JournalofGansuSciences,2016,28(6):89-92.[杨国来,张灿罡,尹大禹,等.锥阀阀口能量损失分析及阀座结构改进[J].甘肃科学学报,2016,28(6):89-92.]

10.16468/j.cnki.issn1004-0366.2016.06.018.

2015-06-15;

2015-08-23.

杨国来(1963-),男,辽宁沈阳人,教授,博士生导师,研究方向为液压元件及自动控制.E-mail:yanggl@lut.cn.

TH

A