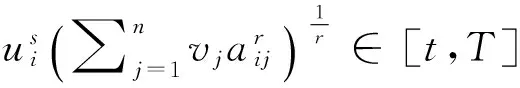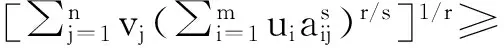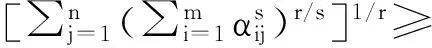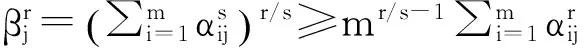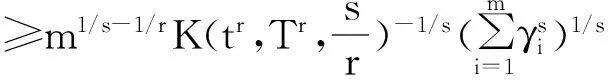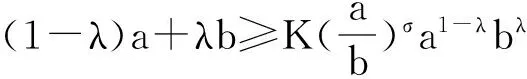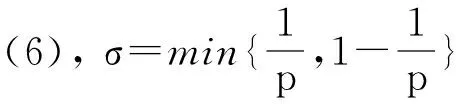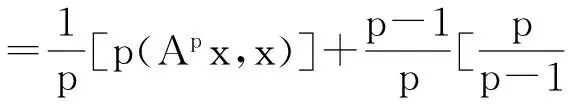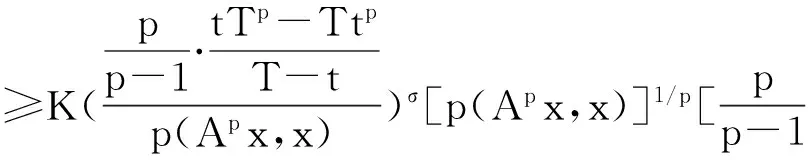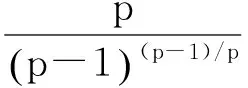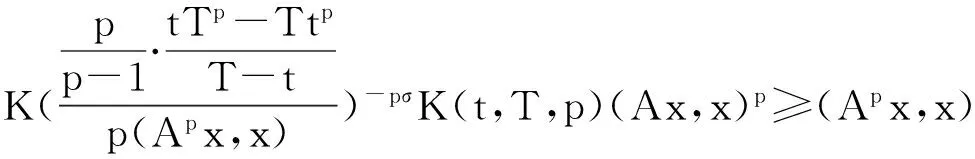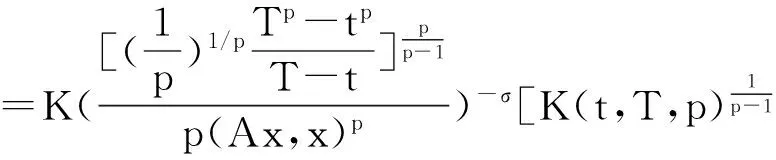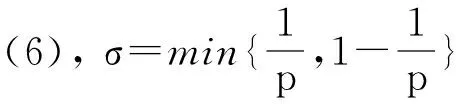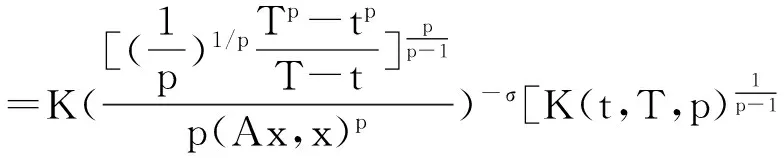几个含有Kantorvich常数的不等式的推广
2016-12-16黄弘
黄 弘
(湖北工程学院 数学与统计学院, 湖北 孝感 432000)
几个含有Kantorvich常数的不等式的推广
黄 弘
(湖北工程学院 数学与统计学院, 湖北 孝感 432000)
运用不等式理论,得到了关于Kantorvich常数的不等式,该结果推广了文献中的相关结论。此外,利用Kantorvich率,也推广了文献中含有Kantorvich常数的不等式。
Kantorvich 常数;Kantorvich率;不等式
近年来,含有Kantorvich常数的不等式成为人们研究的热点[1-4]。设x1,x2,...,xn为非负实数,s>r>0,那么下列幂形式的单调不等式[1]成立:
(1)
文献[2]给出了式(1)的下列结果:
定理1[2]设x1,x2,...,xn∈[t,T],其中0 (2) 这里s>1时,K(t,T,s)为Kantorvich 常数,定义为 (3) 显然,不等式(2)可以看作不等式(1)的反向不等式。 在文献[3]中,给出了下列结果: 定理2[3]设A是正定矩阵,x为单位向量, TI≥A≥tI>0,其中0 K(t,T,p)(Ax,x)p≥(Apx,x) (4) 这里p>1,K(t,T,p)为Kantorvich 常数, I为n阶单位阵(下同)。 在文献[4]中,给出了下列结果: 定理3[4]设A是正定矩阵,x为单位向量, TI≥A≥tI>0,其中0 ≥(Apx,x)-(Ax,x)p 值得说明的是,上式可以写成 (5) 这里p>1,K(t,T,p)为Kantorvich 常数。 本文推广了不等式(2)、(4)、(5)。 我们需要的引理: 引理1[1]设x1,x2,...,xn为非负实数,s>r>0,那么下列不等式成立: 注记 在定理A中令m=r=1,ui=vj=1,对所有的i=1,2,…,n;j=1,2,…,m,我们得到定理1,因此定理4可以看作定理1的推广。 证明:令 我们只需证明 由公式(1),有 (j=1,2,…,n) 注意到 从而 下面我们改进定理4: 引理2[4]设a,b>0,λ∈[0,1],那么下列不等式成立: 这里σ=min{λ,1-λ},K(h)为Kantorvich率,定义为: (6) 引理3[2]设A是正定矩阵,x为单位向量, TI≥A≥tI>0,其中0 这里p>1。 定理5 设A是正定矩阵,x为单位向量, TI≥A≥tI>0,其中0 (7) 证明:由引理3,我们有 于是,得到 ≥(Apx,x)1/p, 该式就是 定理4 设A是正定矩阵,x为单位向量, TI≥A≥tI>0,其中0 (8) 证明:由引理2.3,我们有 [1] Bullen P S, Mitrinovic D S,Vasic P M. Means and their inequalities[M].Springer,1988:143. [2] Yamazaki T. An extension of Specht's theorem via Kantorovich inequality and related results[J]. Mathematical Inequalities and Applications, 2000, 3(1):89-96. [3] Furuta T. Operator inequalities associated with H lder-McCarthy and Kantorovich inequalities[J].Journal of Inequalities and Applications, 1998, 2(2):137-148. [4] Zuo H, Shi G, Fujii M, et al. Refined Young inequality with Kantorovich constant[J]. Journal of Mathematical Inequalities, 2011, 5(4):551-556. (责任编辑:熊文涛) Extension of Several Inequalities Containing Kantorvich Constant Huang Hong (SchoolofMathematicsandStatistics,HubeiEngineeringUniversity,Xiaogan,Hubei432000,China) In this paper, several extensions of some inequalities, including Kantorvich constant, have been established, using new results of inequality theory. At the same time, other inequalities of the same type have been generalized by Kantorvich ratio. Kantorvich constant; Kantorvich ratio; inequality 2016-03-01 黄 弘(1969- ),男,湖北孝昌人,湖北工程学院数学与统计学院讲师,硕士。 O15 A 2095-4824(2016)03-0125-03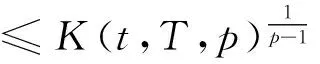
1 引理与主要结果