改进的离散连续优化多目标跟踪
2016-12-16齐美彬潘龙飞蒋建国
齐美彬,潘龙飞,蒋建国
(合肥工业大学计算机与信息学院,合肥230009)
改进的离散连续优化多目标跟踪
齐美彬,潘龙飞,蒋建国
(合肥工业大学计算机与信息学院,合肥230009)
针对多目标跟踪中,目标瞬间丢失、目标交错或重叠时目标跟踪失败等情况,本文提出了一种改进的离散连续优化多目标跟踪算法。该方法根据离散连续优化多目标跟踪算法原理,采用增加速度约束项能量函数以及改进原能量函数的策略,以达到约束轨迹形态的目的。采用在全局优化后进行聚类处理的策略,以达到区分不同目标运动轨迹的目的。实验结果表明,该算法具有较好的鲁棒性,能够很好地实现复杂图像序列中的多目标跟踪。关键词:多目标跟踪;离散连续优化;能量函数
0 引言
多目标跟踪一直是计算机视觉领域热门研究方向之一,广泛应用于视频监控、交通控制等领域。文献[1]对Camshift与卡尔曼滤波进行改进和组合,算法根据目标大小自适应地调整搜索窗口尺寸,通过卡尔曼滤波实现对运动目标位置的估计,提高了对重叠目标跟踪的准确性。文献[2]提出一种基于粒子滤波的多目标跟踪方法,该算法首先通过粒子滤波对每一个目标在下一帧可能出现的范围进行预测,通过建构基于最新观测信息的重要性密度函数,提高算法在目标交叉情况下跟踪的准确性和鲁棒性。文献[3]提出了一种多特征融合匹配的目标跟踪算法。算法将目标特征颜色、质心位置、运动速度等特征进行融合,避免了单一特征匹配的局限性。文献[1-3]的核心跟踪思想为相邻帧目标之间的局部匹配,如果局部匹配出错,将造成后续跟踪失败。针对上述问题,众多学者正在探索新的目标跟踪算法,以克服传统目标跟踪算法的局限性。
文献[4]提出一种基于连续能量函数最小化的多目标跟踪算法,算法设计了一个尽可能表达真实问题的
能量函数,并通过构造一个合适的优化框架来得到能量函数的局部极小值,从而获得最优的跟踪结果。文献[4]将能量函数应用到了多目标跟踪领域,但核心思想仍为局部匹配。AntonAndriyenko等[5]提出了一种基于离散连续优化的多目标跟踪算法,该算法摒弃了基于目标外观模型的特征匹配与局部匹配,基于目标的位置和大小信息将多目标跟踪问题转化为一个全局能量函数最小化问题,并采用离散连续优化方法进行求解,在复杂场景中较传统跟踪方法有更好的鲁棒性。在部分复杂场景中,文献[5]算法出现了部分跟踪错误问题,其鲁棒性仍有待提高。
针对文献[5]中出现的跟踪丢失、跟踪分裂、身份转换和轨迹合并等问题,本文对算法中能量函数加以改进及通过聚类方法对合并轨迹进行优化,提高了目标跟踪的准确度和精确度。
1 相关工作
设D为所有目标集合,定义部分描述D的离散变量。第t帧第j个样本表示为的位置信息与置信度分别为为三次B-样条函数[6],并表示为所有目标轨迹集合,即:


式中:Φ为异常样本集合。
1.1 离散数据关联
离散数据关联即为分配样本标签并建立初始目标轨迹。样本标签分配实现方法为最小化如下能量代价函数:

式中:Ud为数据项,Sd,d'为平滑项[7],式(3)的最小化方法为基于图割的α-膨胀算法[8]。其中数据项为


其中:δ为克罗内克函数,惩罚标签不同的邻居样本。
1.2 轨迹预测
数据关联建立了目标初始轨迹,轨迹预测则为更新初始轨迹。轨迹预测实现方法为最小化如下能量函数:

式中:hf(Γ)为标签代价能量,主要由以下五项组成。
1)动态学项。通常,目标的运动速度受物理约束的限制。文献[5]用三次B-样条函数最大的三次项系数来表示动态学能量。

2)持续性项。一般来说,目标都是从图像边缘进入,从图像边缘消失。该项奖励长的、持续性的轨迹,惩罚短的、间断的轨迹。

式中:si为轨迹的起点,ei为轨迹的终点,表示轨迹端点到图像边缘的距离,v·(e-s)-1惩罚较短的ii轨迹。
3)高阶数据保真度项。该项奖励轨迹靠近检测样本,惩罚轨迹远离检测样本。

式中:Mk为轨迹缺失样本的时间跨度。图1(a)轨迹长时间远离样本,图1(b)轨迹靠近样本。
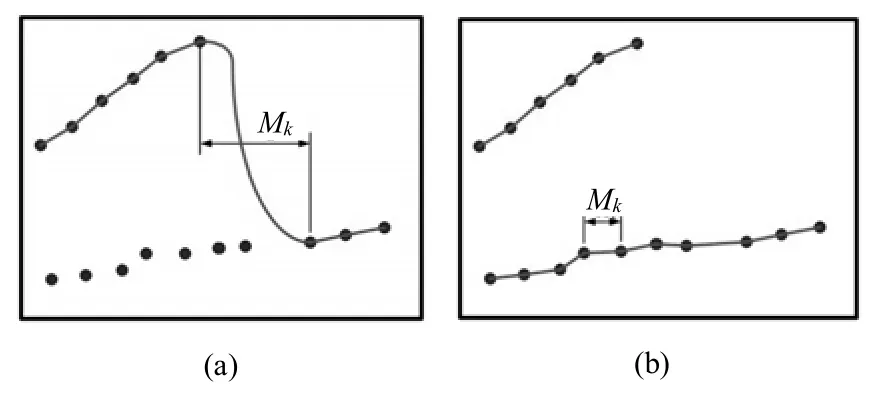
图1 轨迹的时间跨度Fig.1The time spans of trajectory
4)相互排斥项
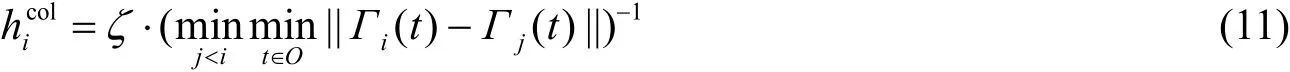
5)正则项。正则项惩罚轨迹的数目,文献[5]中正则项设为常数1。
2 改进的离散连续优化多目标跟踪算法
主要介绍了离散连续优化多目标跟踪算法中的能量函数及优化过程。其中,标签项能量对最终轨迹的生成影响较大。同时,针对文献[5]在部分跟踪场景中存在的问题,提出如下三点改进:
2.1 高阶数据保真度项修改
高阶数据保真度项鼓励轨迹靠近样本,惩罚轨迹长时间远离样本。该项的定义如式(10)所示,式(10)首先对时间跨度求三次方,而后求加权的所有时间跨度的三次立方和。时间跨度指数为对时间跨度的惩罚力度,即鼓励轨迹少出现或不出现时间跨度。因此,适当增大时间跨度指数能进一步迫使轨迹靠近检测样本,从而得到更为准确的轨迹。权重系数ξ为高阶数据保真度项在标签项中所占的比重,若ξ过大,则影响同一目标轨迹片段的融合;若ξ过小,轨迹则将忽略式(10)的惩罚而随机地生成,从而达不到约束轨迹形态的目的。实验表明,在一定范围内,增大指数,减小系数,可提高目标跟踪准确度,但所耗时间也会增大。综合考虑,本文指数设为5,系数设为0.03。高阶数据保真度指数和系数取值适宜、系数过大、指数过小的跟踪效果分别如图2(a)、(b)、(c)所示。图2实验结果表明:当高阶数据保真度项指数与系数取值适宜时,得到的跟踪结果较为理想;当该项系数过大时,轨迹出现了分裂现象;当该项指数偏小时,轨迹偏离检测样本较远,跟踪效果较差。
2.2 速度变化约束项
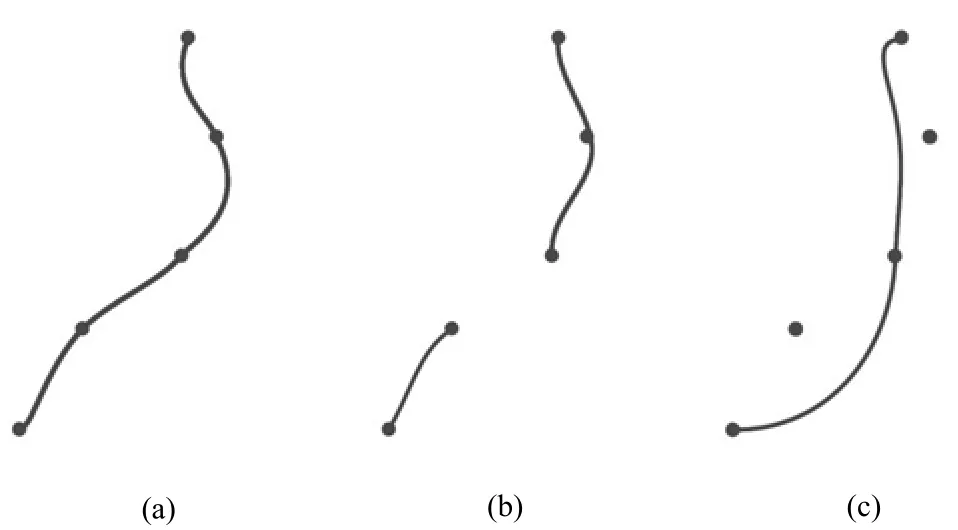
图2 高阶数据保真度系数和指数对跟踪结果的影响Fig.2The influence of coefficientand exponentof high-orderdata fidelityfor tracking results
所有目标的运动都是受物理限制约束的,对于场景中的大部分运动目标,其轨迹是趋于光滑的,即目标的运动速度不会在短时间内发生突变。为了抑制目标的速度发生突变,本文加入了目标速度变化约束项能量函数。线速度与角速度是两个能较好地描述轨迹速度的物理变量,线速度与角速度的变化率则能直观地反映出轨迹物理形态的变化。对于速度发生突变的轨迹,其线速度与角速度的变化率则较大,能量函数惩罚力度较大;而运动符合常理的目标,其线速度与角速度的变化率则较小,能量函数惩罚力度较小。因此,本文在标签项能量中加入轨迹线速度与角速度变化率惩罚的能量函数,进一步约束轨迹的形态。
设x=x(t),y=y(t)为轨迹在第t帧的坐标,则轨迹在时间t的角速度[9]定义如下:

角速度变化率定义为

角速度变化率能量函数为

目标在时间t的线速度定义为

线速度的变化率为

线速度变化率能量函数为

角速度与线速度变化率能量函数奖励速度趋于稳定或变化平缓的轨迹,惩罚速度发生突变的轨迹。通过实验得出当线速度与角速度变化率能量函数系数分别取0.001和0.005时,能取得较为理想的跟踪效果。图3(a)为未加入速度约束项的跟踪结果,图3(b)为加入了速度约束项的跟踪结果,显然,图3(b)的跟踪结果较为理想。
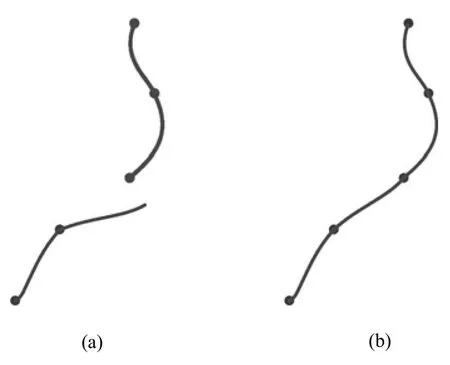
图3 速度约束项对跟踪结果的影响Fig.3The influence of velocity constraintitemfor tracking results
2.3 优化后的聚类
对于存在目标粘连的场景,算法易将不同目标误认为同一目标而得到错误的轨迹。如图4(a),(c)所示,通常,错误轨迹出现在粘连目标之间。对于粘连的目标,需要通过一定的处理,将粘连目标区分开来,进而得到正确的轨迹。对于图4(a)情况,错误轨迹出现在粘连目标上下之间,本文计算曲线上下样本x坐标与中间错误曲线y坐标之差,曲线之上样本坐标差值为正,曲线之下样本坐标差值为负,并按差值符号(正或负)进行聚类,图4(b)上方灰色样本和下方黑色样本各为一类。对于图4(c)情况,错误轨迹出现在粘连目标左右之间,本文则计算中间错误曲线左右样本x坐标与中间曲线y坐标之差,曲线左边样本坐标差值为负,曲线右边样本坐标差值为正,并按差值符号(正或负)进行聚类,图4(d)左边灰色样本和右边黑色样本各为一类。
对于聚类后得到的同一类样本,我们认为是同一个目标,分别对其拟合成三次B-样条曲线,得到目标的运动轨迹,如图4(b)、(d)所示。
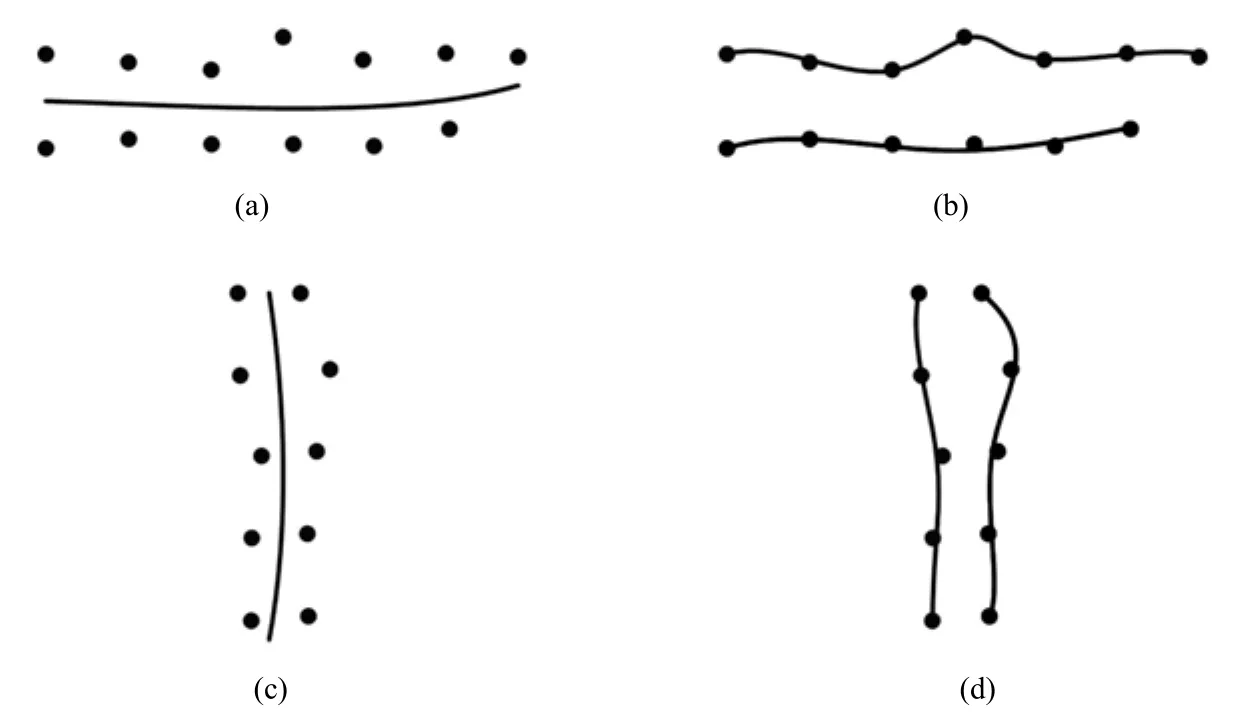
图4 聚类前后的跟踪效果Fig.4The tracking effects before and after clustering
在多个标准测试视频的对比实验结果表明,本文改进后算法与原算法相比,可以达到更高的跟踪精度。
3 实验结果与分析
为了验证本文所改进算法的有效性,分别选用了标准测试视频PETS2009中的四个序列S2L1、S3MF1、S2L2与S1L1进行实验,其帧数分别为795、107、436和220。为了更好地对比,本文分别只选取四个序列中更具挑战性的100帧进行实验,选择的帧号分别为651~750、1~100、1~100和1~100,并在AMD X4 640、主频3.00 GHz、内存4.00 GB的PC机上进行实验,运行平台为Matlab R2012b。
本文算法参数设置:高阶数据保真度项系数ξ和指数分别为0.03和4,原算法对应数据分别为1和3;相互排斥项能量代价较大,本文与原算法一样不予考虑,系数设为0;线速度变化率和角速度变化率能量函数系数分别为0.001和0.005;动态学项、持续性项、正则项系数与原算法保持一致,各项系数都为1。
3.1 算法效果的定性分析
对于S2L1和S3MF1序列,本文给出最终的跟踪结果并作定性对比分析;对于S2L2与S1L1序列,由于序列场景复杂度较高,目标之间的交叉、粘连、遮挡情况出现过于频繁,本文改进后算法与原算法的跟踪准确度都较低,故不给出跟踪结果和定性分析。
在测试序列S2L1中,该测试序列的特点是场景复杂,目标之间的遮挡、交叉较多。遮挡和交叉容易造成检测信息的丢失,从而出现跟踪丢失、跟踪分裂、和身份转换等现象。文献[5]算法与本文改进后算法跟踪结果如图5所示。
三维坐标系的z轴、x轴、y轴分别表示序列的帧数、样本x方向坐标、样本y方向坐标,轨迹的颜色区分不同的目标。图5(a)为文献[5]的跟踪结果,原算法出现了跟踪分裂(图中空心正方形标记的轨迹和实心正方形标记的轨迹)与身份转换(图中空心三角形标记的轨迹和实心三角形标记的轨迹)等现象。图5(b)为本文改进后算法的跟踪结果,本文减小了高阶数据保真度能量函数项系数,保证了同一目标的轨迹片段融合后的标签项能量不会大于未融合之前的总能量,使得同一目标轨迹片段能够融合,从而得到正确的轨迹(图5(b)空心正方形标记的轨迹),且消除了身份转换问题(图5(b)空心三角形标记的轨迹)。
在测试序列S3MF1中,该序列目标数目较多,且目标之间的距离较小,易产生轨迹合并现象。文献[5]与本文改进后算法在S3MF1序列最终的跟踪结果如图6所示。
图6(a)为文献[5]算法的跟踪结果,从图中可以看出,跟踪结果非常混乱,跟踪器出现了在两个目标之间“跳跃式”跟踪(图6(a)空心正方形标记的轨迹)、轨迹合并(图6(a)空心圆形标记的轨迹)以及身份转换(图6(a)空心三角形与实心三角形标记的轨迹)等现象。“跳跃式”跟踪结果产生的原因为轨迹速度发生了突变,
轨迹合并产生的原因为目标距离较近,跟踪器错误地将两个目标当作成了一个目标。图6(b)为本文改进后算法的跟踪结果,本文加入了轨迹角速度和线速度变化率惩罚的能量函数,迫使轨迹速度不能发生突变,从而解决了“跳跃式”跟踪问题(图6(b)空心正方形标记的轨迹和实心正方形标记的轨迹)。聚类处理区分了中间错误轨迹两边的目标(图6(b)空心圆形标记的轨迹和实心圆形标记的轨迹),解决了轨迹合并现象问题。调整了高阶数据保真度能量函数项系数和指数,使同一目标的轨迹能够融合在一起,从而解决了目标身份转换的现象(图6(b)空心三角形标记的轨迹)。
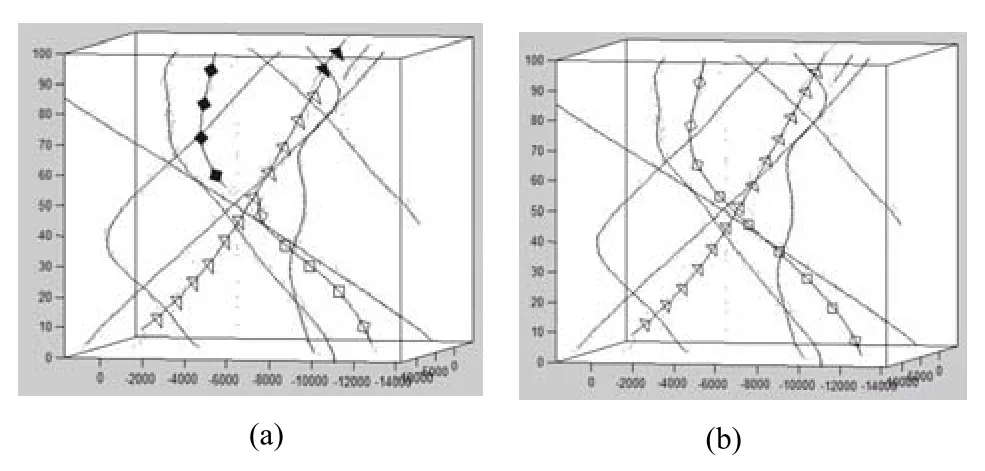
图5 S2L1序列的跟踪结果Fig.5The tracking results on S2L1 sequence
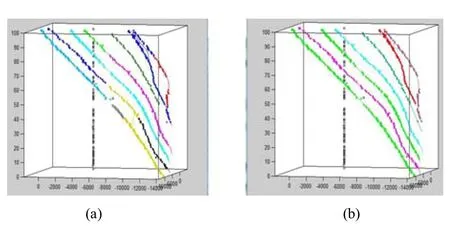
图6 S3MF1序列的跟踪结果Fig.6The tracking results on S3MF1 sequence

表1 S2L1、S3MF1、S2L2、S1L1序列各项指标对比Table 1The indicators comparison on S2L1,S3MF1,S2L2 and S1L1 sequence

图7 本文算法在S2L1与S3MF1数据集上的跟踪示例Fig.7Example frames from our approach on S2L1 and S3MF1 datasets
3.2 算法效果的定量分析
采用目标跟踪的准确度(MOTA)和目标跟踪的精确度(MOTP)来定量评估算法性能[10]。MOTA包括目标丢失、错误警告、身份转换。MOTP为重叠度,即计算跟踪结果区域与目标的真实区域之间的比值。此外,本文还加入了几项指标,分别为:大部分跟踪上的轨迹数(MT),大部分丢失的轨迹数(ML),跟踪分裂次数(FM),身份转换次数(IDs),跟踪错误位置个数(FP)。FM、IDs与FP直接影响目标跟踪准确度,FP影响目标跟踪精确度。表1为两种算法在不同测试序列上跟踪结果的对比,表中粗体代表最佳结果。图7为本文
算法在S2L1与S3MF1[11]数据集上的跟踪示例。
由表1可以看出,在四个测试序列中,本文改进后算法与文献[5]相比,大部分指标有不同程度的提高。在S2L1序列中,本文没有出现跟踪分裂与身份转换现象,跟踪准确度与跟踪精确度有小幅度提高。在S3MF1序列中,消除了目标速度突变和轨迹合并的现象,本文改进后算法各项指标有相当明显的提高,其中,跟踪准确度提高尤为明显。在S2L2序列中,虽然部分指标有所降低,但总体跟踪效果仍有提高。在S1L1序列中,本文解决了部分由目标粘连引起的轨迹合并问题,跟踪准确度提高幅度较大。大量实验结果验证了本文改进后算法在应对不同复杂场景时,较原算法具有更好的鲁棒性。
4 结论
本文针对离散连续优化多目标跟踪算法中存在的问题,提出了一种改进算法。通过增加新的能量函数、改进原能量函数、以及增加全局优化后的聚类,解决了部分目标跟踪中常见的问题。在多个实验测试序列中,与文献[5]的对比实验结果表明,本文算法具有更高的跟踪准确度和跟踪精确度。然而,面对更为复杂的场景,本文算法的鲁棒性还有待提高。在以后的工作中,将加入更多的能量函数来适应不同的跟踪场景,进一步提高算法的鲁棒性。
[1]孙凯,刘士荣.多目标跟踪的改进Camshift/卡尔曼滤波组合算法[J].信息与控制,2009,38(1):9-14. SUN Kai,LIU Shirong.Combined Algorithm with Modified Camshift and Kalman Filter for Multi-object Tracking[J]. Information and Control,2009,38(1):9-14.
[2]高世伟,郭雷,杨宁,等.一种新的粒子滤波目标跟踪算法[J].上海交通大学学报,2009,43(3):485-489. GAO Shiwei,GUO Lei,YANG Ning,et al.A New Particle Filter Object Tracking Algorithm[J].Journal of Shanghai JiaoTong University,2009,43(3):485-489.
[3]王欢,王江涛,任明武,等.一种鲁棒的多特征融合目标跟踪新算法[J].中国图象图形学报,2009,14(3):489-498. WANG Huan,WANG Jiangtao,REN Mingwu,et al.A New Robust Object Tracking Algorithm by FusingMulti-features[J]. Journal of Image and Graphics,2009,14(3):489-498.
[4]Andriyenko A,Schindler K.Multi-target Tracking by Continuous Energy Minimization[C]//Computer Vision and Pattern Recognition(CVPR),Colorado Springs,CO,USA,June 21-23,2011:1265-1272.
[5]Andriyenko A,Schindler K,Roth S.Discrete-continuous optimization for multi-target tracking[C]//Computer Vision and Pattern Recognition(CVPR),Providence,RI,June 16-21,2012:1926-1933.
[6]施锡泉,赵岩.双三次B样条曲面的G~1连续条件[J].计算机辅助设计与图形学学报,2002,14(7):676-682. SHI Xiquan,ZHAO Yan.G1 Continuity Conditions of Bicubic B-Spline Surfaces[J].Journal of Computer-Aided Design& Computer Graphics,2002,14(7):676-682.
[7]Boykov O,Veksler Y,Zabih R.Fast Approximate Energy Minimization Via Graph Cuts[C]//Computer Vision,The Proceedings of the Seventh IEEE International Conference on,Kerkyra,Sept 20-27,1999:1222-1239.
[8]Delong A,Osokin A,Isack H N,et al.Fast Approximate Energy Minimization With Label Costs[C]//Computer Vision and Pattern Recognition(CVPR),San Francisco,CA,June 13-18,2010:2173-2180.
[9]Milan A,Schindler K,Roth S.Detection-and Trajectory-Level Exclusion in Multiple Object Tracking[C]//Computer Vision and Pattern Recognition(CVPR),Portland,OR,June 23-28,2013:3682-3689.
[10]Milan A,Schindler K,Roth S.Challenges of Ground Truth Evaluation of Multi-target Tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition Workshops(CVPRW),Portland,OR,June 23-28,2013:735-742.
[11]http://motchallenge.net/data/3D_MOT_2015/.
The Improved Discrete Continuous Optimization for Multi-target Tracking
QI Meibin,PAN Longfei,JIANG Jianguo
(School of Computer and Information,Hefei University of Technology,Hefei 230009,China)
Aiming at several problems occurred in multi-target tracking,such as the moving targets interleaving or overlapping,and the target losing momentarily,an improved discrete continuous optimization for multi-target tracking algorithm is proposed.The method according to the principle of discrete continuous optimization for multiple target tracking,added speed constraints and ameliorated the original energy function,so as to achieve the purpose of constraint the trajectories form.Clustering strategies after global optimization is used to achieve the purpose of distinguishing different trajectories.The experimental results show that the algorithm has better robustness and can well realize multi-target tracking in complex image sequences.
multi-target tracking;discrete continuous optimization;energy function
1003-501X(2016)07-0009-07
TP301.6
A
10.3969/j.issn.1003-501X.2016.07.002
2015-08-11;
2015-11-20
国家自然科学基金项目(61371155);安徽省科技攻关项目(1301B042023)
齐美彬(1969-),男(汉族),安徽东至人。教授,博士,主要研究智能视频监控、DSP技术及应用。E-mail:qimeibin@163.com。
潘龙飞(1991-),男(汉族),江西赣州人。硕士研究生,主要研究工作是目标跟踪。E-mail:feifei_lengleng@sina.com。
