FIR滤波器与回归分析的空间外差干涉谱目标识别

张文涛，高凤艳，叶松，熊伟，汪杰君，王新强

(1.桂林电子科技大学电子工程与自动化学院，广西桂林541004；2.中国科学院安徽光学精密机械研究所，合肥230031；3.广西高校光电信息处理重点实验室(桂林电子科技大学)，广西桂林541004)

FIR滤波器与回归分析的空间外差干涉谱目标识别

张文涛1,3，高凤艳1,3，叶松1,3，熊伟2，汪杰君1,3，王新强1,3

(1.桂林电子科技大学电子工程与自动化学院，广西桂林541004；2.中国科学院安徽光学精密机械研究所，合肥230031；3.广西高校光电信息处理重点实验室(桂林电子科技大学)，广西桂林541004)

结合辐射传输和朗伯比尔定律，提出一种基于有限脉冲响应数字滤波器和多元线性回归分析的空间外差干涉谱目标匹配方法，通过对干涉图直接分析来提取出钾共振双线的特征以实现目标识别。本文采用传统有限脉冲响应数字滤波的处理方法来消除有效目标干涉频率信息以外的背景信息和干扰信号。通过对滤波前后的时域干涉数据进行多元线性回归处理获得最佳的时域滤波系数，以对目标信号、背景信号的干涉图直接进行滤波处理，最后通过干涉图匹配技术来识别钾共振双线信号。该算法无需测量背景光谱或背景干涉图，亦无需对干涉图做傅里叶变换获取光谱，在提高计算效率的同时提高空间外差光谱仪遥感数据的分析反演能力。

空间外差光谱技术；干涉图；钾共振双线；有限脉冲响应数字滤波器；多元线性回归

0 引言

空间外差光谱技术(Spatial Heterodyne Spectroscopy，SHS)集成空间调制干涉技术和光栅衍射技术于一体，是一种新型的可实现超高光谱分辨率的遥感技术，同时还具有高通量、空间光栅衍射、无运动部件、集成度高、体积小、重量轻等特点，使其在大气痕量气体的精细谱线探测和复杂背景下微弱目标信号探测以及定量反演方面具有明显优势[1-4]。国内外包括美国威斯康辛大学、加拿大宇航局以及中科院安光所等研究机构均开展了针对大气遥感观测的空间外差光谱技术研究[5-7]。

对于复杂背景下的微弱信号的遥感探测，早在1997年国内研究者利用差谱法对通过傅里叶变换红外遥感技术探测到的微弱目标分析物进行目标识别[8]。利用差谱法需要事先获得背景光谱，因此针对动态目标或无背景获取的条件下，难以实现对目标分析物的探测与识别，而且移动平台上收集的数据也需要更加复杂的数据处理方法。在实际应用中如果需要实时的光谱数据处理过程，傅里叶变换使得计算效率降低，这就要求在消除傅里叶变换的情况下研究一种直接对干涉图分析处理的方法。美国的G.W.Small和中科院安徽光机所都开展过基于FTS干涉图分析的目标识别方法[9-12]。但就SHS而言，在获得精细的光谱信息的同时可以更真实的识别物质的光谱本征信息，因此需要研究一种直接对SHS干涉图分析的处理方法。

本文利用空间外差光谱仪对钾共振双线干涉信号进行探测识别。结合辐射传输与朗伯比尔定律提出基于SHS干涉图分析的目标识别方法，通过对时域滤波前后的干涉信息进行多元线性回归分析求解滤波系数，最后对有无目标信号的干涉图进行匹配计算实现目标信息的有效识别。该方法允许SHS光谱仪可在移动平台上运行，同时无需获取背景信息和复杂的数据处理。

1 理论基础

1.1 空间外差光谱仪结构原理

空间外差光谱仪干涉原理如图1所示，它采用两个衍射光栅代替传统迈克尔逊干涉仪的两个平面反射镜。它以空间调制方式分解两个相干光束产生频域外差干涉。在空域面形成的二维干涉条纹最终由探测器接收，探测器记录的干涉条纹经过傅里叶变换即可获得被测光谱曲线。

图1 空间外差光谱仪原理图Fig.1Schematic diagram of the SHS configuration

1.2 干涉图基本原理

空间外差光谱仪对大气中的目标信号进行探测时，光谱仪接收到的大气辐射信号既包含目标信号，还包含大气以及背景信号。根据辐射传输和朗伯比尔定律，在不考虑仪器偏置的情况下，光谱仪最终测得的光谱可表示[13]

其中：R是探测器的仪器响应函数；Lb是背景辐射信号；Lo是目标辐射信号。

SHS光谱仪输出的是干涉图信息，即CCD探测器得到的干涉图可表示为[14]

SHS干涉图为在记录位置x处两相干波前的光程差u的函数：

令σ＇=σ-σ0，则式(2)表示为

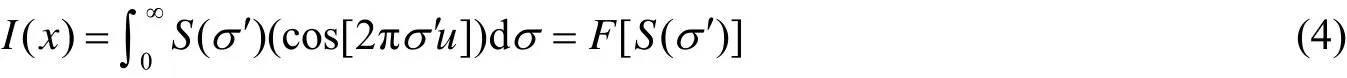
将式(1)带入式(4)可得：

由式(5)可知：干涉图表示背景以及目标信号辐射谱傅里叶变换后两项叠加的形式。为了获取目标信号的特征信息必须将背景信息去除掉。在传统背景光谱或背景干涉图可测的情况下通常选择差谱法来进行目标特征信息的提取；但在实际应用环境中，遥感探测系统在移动平台上很难获得稳定的背景光谱或背景干涉图，这就要求研究出一种可直接对干涉图时域滤波的处理方法来进行背景信息的扣除，以便对目标信号的识别与匹配。

1.3 时域数字滤波器

获取的干涉数据实际是余弦信号的总和。对干涉图进行时域滤波可以抑制特定频率信号的幅值，同时放大其它频率信号的幅值。然而想要获得实用的时域滤波器首先要对光谱数据进行频域滤波。时域数字滤波器的频率响应函数为频域滤波器，频域滤波器乘以光谱再经过逆傅里叶变换后对应滤波后的时域信号：

其中：y(t)为滤波后的干涉图，H(f)X(f)为滤波后的光谱图，H(f)为滤波器的频率响应，X(f)为光谱图，x(t-k)为原始干涉图，h(k)为滤波器频率响应H(f)的逆傅里叶变换。在时域与频域间通过逆傅里叶变换F-1来转换。

以上方程对应连续函数的形式。对于离散化数据其形式为

其中：yt为滤波后干涉图点t的强度，hk和xt-k分别对应相应函数的离散点和原始干涉图点。yt和xt分别对应滤波后与滤波前干涉图。由于干涉图的采样点数总是有限的，因此卷积积分的离散形式必须通过有限序列来近似，得到的近似形式为

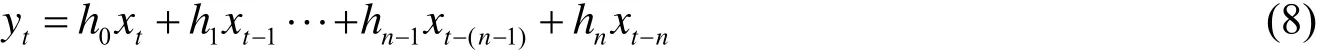
其中：yt为原始数据干涉图xt及其周围数据点的n+1项的总和，hk对应滤波器频率的权重系数。式(8)说明每个滤波后的干涉点都是原始数据点与一组先前的原始数据点的线性组合。这种典型的滤波器为有限脉冲响应(Finite Impulse Response，FIR)滤波器，它是非递归差分滤波器的形式。

1.4 多元线性回归分析

多元线性回归分析是统计学的一个分支，是对自变量与因变量间的相关关系研究的一种统计[15]。在研究中，滤波后的干涉点yt是因变量，原始干涉点xt为自变量，hk为经过多元线性回归分析计算得到的回归系数。由于FIR滤波器为差分方程形式的滤波器，也就是说输出序列的每一项均为前项序列的函数，在进行多元线性回归分析时要对自变量xt进行循环移位生成(n+1)(n+1)矩阵。因此在回归分析中，hk通过下式产生：

其中：X为原始干涉数据的矩阵形式，其列向量为自变量；XT为X的转置；Y为因变量；h为回归系数。

1.5 干涉图匹配

在遥感、地物光谱等应用中，光谱匹配是目标识别中非常重要的环节。利用干涉图匹配技术代替光谱匹配技术可以省去傅里叶变换过程，即不用进行光谱复原，节省了运算效率。根据Kruse提出的光谱角度匹配(SpectralAngle Match，SAM)原理，通过计算两个矢量的广义夹角：

来表示匹配程度，夹角越小表明地物越相似[16]，等于0说明两个干涉图相同，即两个光谱分布一致；反之，说明两个干涉图相似程度越低，即两个光谱分布不一样。

2 算法描述

时域干涉数据滤波的算法核心在于滤波系数的产生。即从频域开始，利用高斯频域滤波可以保留有用的目标信号，从而其他无用信号被去除。利用多元线性回归分析对生成的原始干涉信号与滤波后的干涉信号进行近似求解得到滤波系数。最后通过干涉图匹配技术对目标识别，以提取出目标信号。

算法描述如图2所示，流程如下：

1)在对目标特征信息提取与识别之前应先对原始干涉图进行去基线和切趾预处理。

2)由式(5)可知原始干涉图是由目标与背景光谱叠加后经傅里叶变换得到，根据目标光谱信号的特征峰与谱线宽度设置高斯频域滤波器的参数。

3)高斯频域滤波器与原始光谱相乘就保留了目标信号，其他信号被去除。对保留的目标信号通过式(6)进行傅里叶变换就得到了滤波后的时域干涉信息。

4)由于滤波后的干涉数据的零光程差在点1处，原始干涉数据必须将零光程差点移到点1处，这样在回归分析中才能建立对应关系。

5)将原始干涉数据生成n+1行n+1列的自变量矩阵，滤波后的干涉数据生成n+1行1列矩阵，通过对因变量与自变量进行多元线性回归分析求解最佳滤波系数(回归系数)。

利用生成的滤波系数分别对原始、背景以及水汽干扰信号的干涉图直接进行滤波处理，实现干涉图匹配，得到识别结果。

图2 算法流程图Fig.2Algorithm chart

3 实验结果分析

为了对以上算法进行验证，本文使用中国科学院安徽光机所研制的空间外差光谱仪对钾盐燃烧光谱进行观测。空间外差光谱仪的主要参数为：光栅Littrow波长771 nm；光谱范围745 nm～771 nm；光谱分辨率约0.08 nm。钾线光谱的两个辐射特征峰为766.5 nm和769.9 nm。

图3 原始干涉图Fig.3Raw interferogram

3.1 干涉图处理

通过SHS光谱仪观测得到的原始干涉图如图3所示，它们分别为钾共振双线以及大气背景干涉图，都

是空间域数据。通过对实验中由CCD产生的不均匀性进行校正而得到的二维干涉图样。

本文对测量得到原始二维干涉图的中间一条干涉图进行数据处理，对应钾共振双线每条干涉图的光谱信号是由有效的目标信号与背景信号叠加而成。图4显示原始的辐射光谱图、背景光谱图以及二者的差谱图(目标)。可以很明显的看到钾共振双线特征峰在光谱图的766.5 nm和769.9 nm处，同时光谱图中存在背景以及其他干扰信号的作用。

式(5)的第一项为背景辐射谱的干涉图，第二项为钾共振双线辐射谱的干涉图；如图5所示，两个干涉信号随着光程差的增加衰减为0的速率并没有太大区别，不能直接从干涉信号中区别二者的差异。所以就要求设计出一种可以直接对干涉图滤波的处理方法来识别出目标信号。

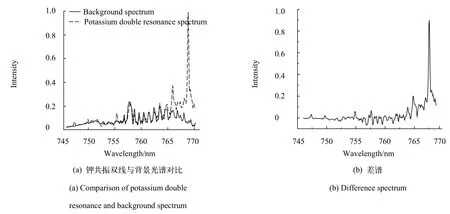
图4 钾共振双线光谱与背景光谱Fig.4Potassium double resonance spectrum and background spectrum

图5 钾共振双线与背景光谱对应的干涉图Fig.5Fourier transform interferogram of potassium double resonance and background spectrum

3.2 信号滤波处理

频域滤波器的通带中心在钾共振双线信号的光谱辐射峰处，频率响应的半峰宽分别设置为0.5 nm和0.5 nm。频域滤波器实际上是与钾共振双线曲线相同的中心在两个特征峰处的高斯曲线，将高斯频率响应滤波器与光谱相乘，就保留了钾共振双线信号，与钾共振双线无关的其余信号被去除，如图6所示。

在本文中，因变量为预期的高斯频域滤波器乘以光谱再经过逆傅里叶变换得到滤波后的干涉图，如图7所示；自变量就是原始干涉图。最佳时域滤波系数可以通过多元线性回归分析来计算。产生的时域滤波器可以运行在任意一条干涉图中。

图6 高斯频域滤波器Fig.6Action of Gaussian frequency filter

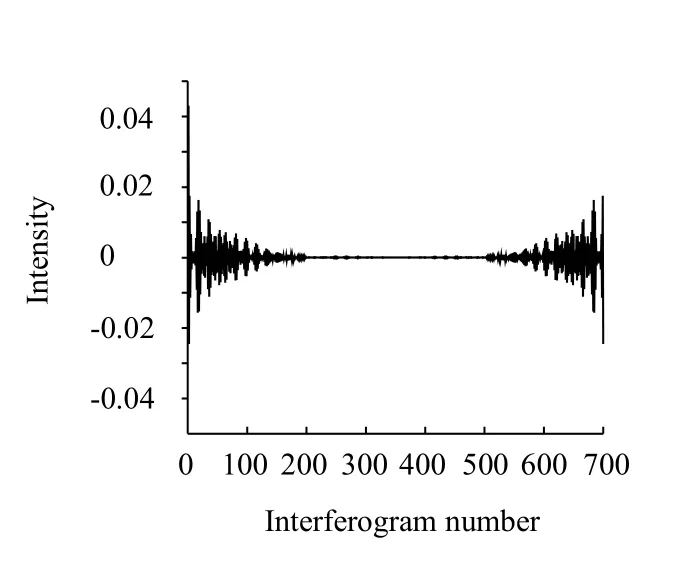
图7 滤波后的光谱逆傅里叶变换Fig.7Inverse Fourier transform of filtered spectrum

3.3 多元线性回归分析

在多元线性回归分析中，对产生的自变量与因变量之间进行回归处理得到近似的回归系数(滤波系数)。在傅里叶变换之前，利用滤波系数(回归系数)直接对干涉图进行滤波，滤波后的干涉图如图8(a)所示，经过傅里叶变换得到滤波后的光谱如图8(b)所示。图8(b)和图6(b)中经过频域滤波后得到的光谱只存在细微的差异，只是经过时域滤波的光谱存在一些基线噪声分量，但钾共振双线信号的两个特征峰被保留，足以说明通过设计的时域滤波器可以提取出钾共振双线信号。

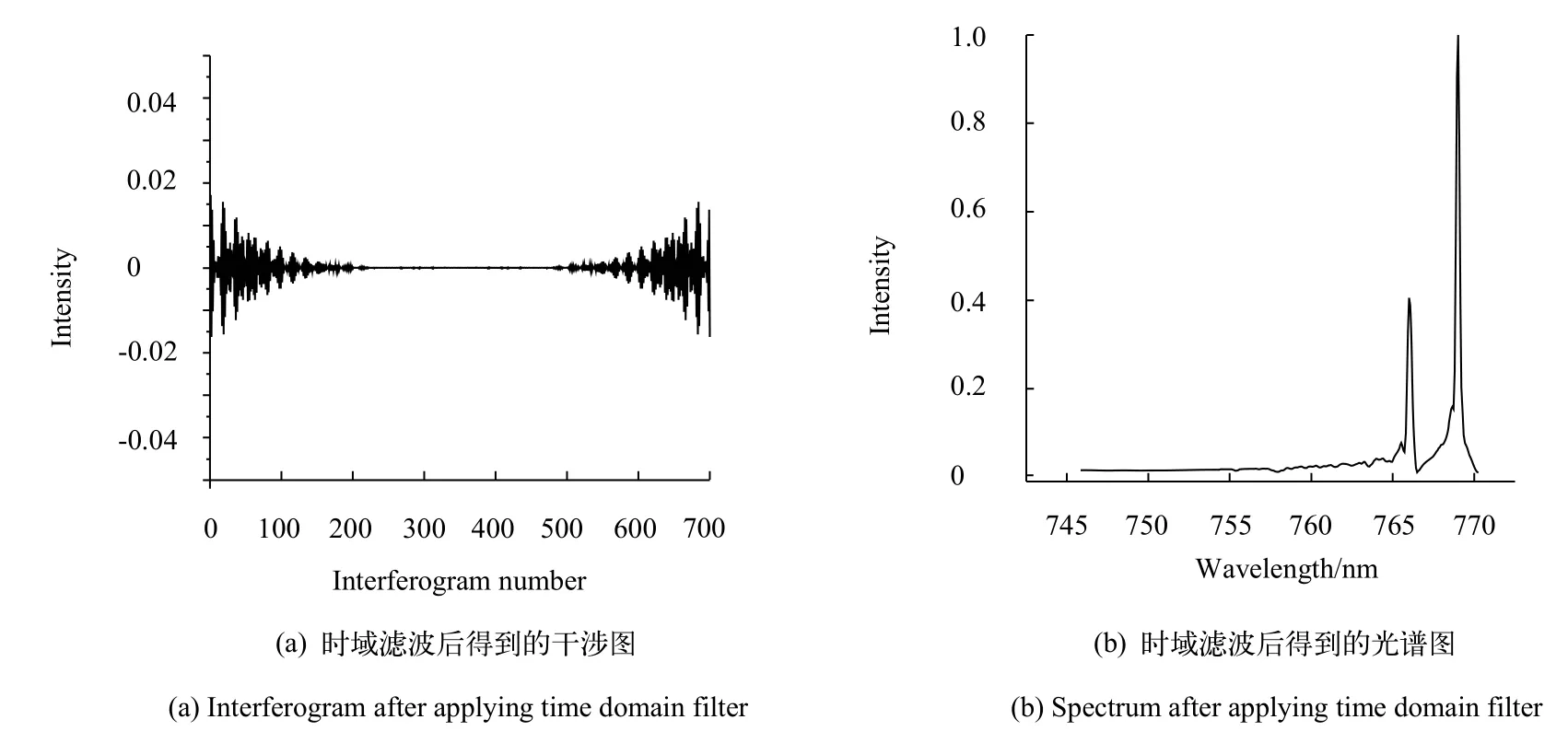
图8 时域滤波处理Fig.8Action of time domain filter

对背景信号以及差谱信号的干涉图直接利用得到的时域滤波系数进行滤波，得到的滤波后的干涉图如图9所示。经过时域滤波后的干涉图差谱与图8(a)的干涉图大致相同；而背景信号与其两者有很大差别，可以直接从干涉图中区别它们的差异。通过式(10)分别计算原始信号与背景信号以及原始信号与差谱信号间的相似度，如表1所示。由此可知，经过时域滤波的原始干涉图与差谱干涉图计算的相似度为0.148，而原始干涉图与背景干涉图的相似度为0.652 9，说明原始干涉图与差谱干涉图更匹配。

3.4 干涉图匹配计算

利用所设计的传统时域滤波器分别对钾共振双线原始信号以及背景信号的总共1 400条干涉图进行滤波，两种干涉图信号均包含700条。对滤波后的1 400条干涉图与图8(a)经过时域滤波后的干涉图分别利用式(10)进行相似度计算，实现干涉图匹配。由图10计算的相似度可知，在选取0.5为阈值的情况下，对

目标信号预测的准确率可达100%。说明利用设计的时域滤波器直接对干涉图滤波是可行的，可以从背景信号中完全识别出钾共振双线目标信号。

图9 时域滤波后的干涉图对比Fig.9Relative intensity of the filtered interferogram

表1 时域滤波后的干涉图间的相似度Table 1Similarity of interferogram after applying the time domain filter

图10 相似度计算结果Fig.10The resulting of similarity

4 结论

以上的时域滤波处理过程可以用于目标信号的提取，该方法不需要获得稳定的背景光谱。滤波系数可以根据不同的目标进行适当的修改整理。时域滤波器的设计是在基于频域滤波的基础上发展而来。就计算效率而言，时域滤波方法去除了傅里叶变换的处理过程，使得干涉信号处理更快，因此可以进一步提高大气目标信号的探测识别速度。

传统的光谱识别方法受背景信号、仪器噪声的干扰，在一定程度上限制了空间外差光谱技术的广泛应用。本文的算法不需要预先测量背景光谱或背景干涉图，实现了目标信号空间外差干涉图特征信息的有效提取。同时该算法简单，缩短计算时间，可以进行快速的实时识别。

[1]Harris W H，Roesle F L，Harlander J M.Applications of reflective spatial heterodyne spectroscopy to UV exploration in the solar system[J].Proceedings of SPIE，UV and Gamma-Ray Space Telescope Syetem(S0277-786X)，2004，5488：886.

[2]罗海燕，施海亮，李志伟，等.空间外差光谱仪中窄带滤光片的光谱特性研究[J].光谱学与光谱分析，2015，35(4)：1116-1119. LUO Haiyan，SHI Hailiang，LI Zhiwei，et al.Study on the Spectral Characteristics of the Narrow-Band Filter in SHS[J]. Spectroscopy and SpectralAnalysis，2015，35(4)：1116-1119.

[3]叶松，熊伟，乔延利，等.空间外差光谱仪干涉图数据处理[J].光谱学与光谱分析，2009，29(3)：848-852.

YE Song，XIONG Wei，QIAO Yanli，et al.Data Processing for interferogram of Spatial Heterodyne Spectrometer[J]. Spectroscopy and SpectralAnalysis，2009，29(3)：848-852.

[4]李双，裘桢炜，王相京.星载大气主要温室气体监测仪杂光模拟分析[J].红外与激光工程，2015，44(2)：616-619. LI Shuang，QIU Zhenwei，WANG Xiangjing.Stray light simulation and analysis of space-borne spatial heterodyne spectrometer for monitoring greenhouse gases[J].Infrared and Laser Engineering，2015，44(2)：616-619.

[5]方勇华，荀毓龙.微弱光谱信号的探测与识别[J].红外技术，1997，19(1)：21-25. FANG Younghua，XUN Yulong.Detection and identification of tiny spectral signal[J].Infrared Technology，1997，19(1)：21-25.

[6]LIN Yunlong，Shepherd G，Solgeim B，et al.Introduction to spatial heterdyne obervations of water(SHOW)project and its instrument development[C]//ITSC-X Proceedings，Beijing，China，May 25-31，2005：835-843.

[7]叶松.空间外差光谱技术研究[D].合肥：中国科学院安徽光学精密机械研究所，2007：10-24. YE Song.Study of Spatial Heterodyne Spectroscopy[D].Hefei：Anhui Institute of Optics and Fine Mechanics，CAS，2007：10-24.

[8]熊伟，施海亮，俞能海，等.空间外差干涉光谱仪仪器线型函数测量新方法研究[J].光谱学与光谱分析，2015，35(1)：267-271. XIONG Wei，SHI Hailiang，YU Nenghai，et al.Study on a New Method for Intrumental Line Shape Measurement of Spatial Heterodyne Interference Spectrometer[J].Spectrcoscopy and SpectralAnalysis，2015，35(1)：267-271.

[9]Tarumi T，Small G W，Combs R J，et al.Digital filtering implementations for the detection of broad spectral features by direct analysis of passive Fourier trandform interferodrams[J].Applied Spectroscopy(S0096-8706)，2004，58(4)：432-441.

[10]Taruni T，Small G W，Combs R J，et al.Infinite impulse response filters for direct analysis of interferogram data from airborne passive Fourier transform infrared spectrometry[J].Vibrational Spectroscopy(S0924-2031)，2005，37(1)：39-52.

[11]沈明蓬，方勇华，黄烨，等.基于干涉图分析的大气污染气体探测[J].量子电子学报，2006，23(25)：707-710. SHEN Mingpeng，FANG Yonghua，HUANG Ye，et al.Based on the analysis of interferogram detecting air pollution gases[J]. Journal of Quantum Electronics，2006，23(25)：707-710.

[12]焦洋，徐亮，高闽光，等.污染气体扫描成像红外被动遥测系统实时数据处理研究[J].物理学报，2013，62(14)：1-7. JIAO Yang，XU Liang，GAO Minguang，et al.Real-time data processing of remote measurement of air pollution by infrared passive scanning imaging system[J].Acta Physica Sinica，2013，62(14)：1-7.

[13]虞莉娟，熊伟，熊惠民.基于独立成分分析的被动红外光谱弱信号检测[J].激光与红外，2008，38(3)：289-292. YU Lijuan，XIONG Wei，XIONG Huimin.Weak Signal Feature Extraction Algoithm for Passive Infrared Spectra[J].Laser& Nfrared，2008，38(3)：289-292.

[14]韦秋叶，王先华，叶函函，等.应用于高精度大气CO2遥感的空间外差技术研究[J].光学学报，2014，34(8)：0801006-1-0801006-6. WEI Qiuye，WANG Xianhua，YE Hanhan，et al.Research of Spatial Heterodyne Spectroscopy for Atmospheric CO2Remote Sensing with High Precision[J].Acta Optica Sinica，2014，34(8)：0801006-1-0801006-6.

[15]吴迪.基于独立成分分析的气体识别方法研究[D].哈尔滨：哈尔滨工业大学，2008：18-19. WU Di.Reasearch on gas detection using independent component analysis[D].Harbin：Harbin Institute of Technology，2008：18-19.

[16]Kruse F A.The spectral imag process-ing system(SIPS)Interactive visualiza-tion and analysis of imaging spectrometer data[J]. Remote Sensing of Environment(S0034-4257)，1993，44(3)：145-163.

Target Recognition on the Finite Impulse Response and RegressionAnalysis from Spatial Heterodyne Spectrometer ZHANG Wentao1,3，GAO Fengyan1,3，YE Song1,3，XIONG Wei2，

WANG Jiejun1,3，WANG Xinqiang1,3
(1.School of Electronic Engineering and Automation,Guilin University of Electronic Technology, Guilin541004,Guangxi Zhuang,China；2.Anhui Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Hefei230031,China；3.Guangxi Colleges and Universities Key Laboratory of Optoelectronic Information Processing, (Guilin University of Electronic Technology),Guilin541004,Guangxi Zhuang,China)

The algorithm of spatial heterodyne interferogram matching on finite impulse response and multiple linear regression analysis is proposed based on the radiation transfer model and Beer-Lambert law.For object identification,we extracted the characteristic of potassium double resonance from analyze interferogram directly.Traditional finite impulse response digital filter processing method was adopted to eliminate background information and other interfered information which except from interference frequency information of effective target.By multiple linear regression analysis processing interference data of time-domain of before and after filtering,the optimal coefficients of time-domain filtering had been obtained.So that,interferograms of target signals and background signals were filtered directly.Finally,

spatial heterodyne spectrometer;interferogram;potassium double resonance;finite impulse response; multivariate linear regression

O433

A

10.3969/j.issn.1003-501X.2016.07.001

1003-501X(2016)07-0001-08

2015-08-30；

2015-11-10

国家自然科学基金(41201342)；广西自然科学基金(2013GXNSFAA019328)；广西自动检测技术与仪器重点实验室基金(YQ14101)资助项目；桂林电子科技大学创新团队资助项目

张文涛(1976-)，男(汉族)，山东济南人。教授，博士，主要从事光电探测方面的研究工作。E-mail：glietzwt@163.com。

叶松(1979-)，男(汉族)，广西桂林人。研究员，博士，主要从事光学遥感方面的研究工作。E-mail：yesongmail@sina.com。

the signal of potassium double resonance was identified by the interferogram matching.In this algorithm,it’s not required measuring the spectrum and interference pattern of background,neither Fourier transforming of interferogram to access spectrum,and improved efficiency and increased inverting capacity of spatial heterodyne spectroscopy analysis remote sensing data simultaneously.