导向钻井工具姿态动态测量的自适应滤波方法

贺 艳，汪跃龙，高 怡，王 彤，李雨丹

(1.西安石油大学 电子工程学院，陕西 西安 710065；2.陕西电子科技职业学院，陕西 西安 710125)



导向钻井工具姿态动态测量的自适应滤波方法

贺 艳1，2，汪跃龙1，高 怡1，王 彤1，李雨丹1

(1.西安石油大学 电子工程学院，陕西 西安 710065；2.陕西电子科技职业学院，陕西 西安 710125)

垂直导向钻井工具在近钻头振动和工具旋转的钻井工作状态下，工具姿态参数的动态测量精度不高。为此，通过理论分析和数值仿真，提出了转速补偿的算法以消除工具旋转对测量的影响；采用最小均方算法(Least Mean Square—LMS)自适应滤波算法，可以有效滤除近钻头振动对测量的影响。数值仿真表明，经过转速补偿和LMS自适应滤波后的井斜角测量误差可小于0.1°，工具面角测量误差小于6°，有效地提高了垂直导向钻井工具的动态测量精度。

导向钻井工具；动态姿态测量；LMS算法；自适应滤波器

贺艳，汪跃龙，高怡，等.导向钻井工具姿态动态测量的自适应滤波方法[J].西安石油大学学报(自然科学版)，2016，31(6)：108-113.

HE Yan,WANG Yuelong,GAO Yi,et al.Adaptive filtering method for dynamic measurement of steering drilling tool attitude[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(6):108-113.

引 言

自动垂直导向钻井是在钻柱旋转作业状态下实现井眼轨迹导向控制的一种全新钻井技术[1]。钻井过程中，自动垂直导向钻井工具(以下简称导向工具)通过控制导向块在给定方位产生导向所需的导向力，达到稳直或纠斜的目的，从而控制井眼轨迹、造成垂直井眼[2]。因此，井下控制系统需要根据导向工具的井下姿态参数(即井斜角 、工具面角)等进行反馈控制，从而确保井眼轨迹的动态稳定[3]。所以井下姿态的实时测量至关重要，是导向工具实现实时导向控制的前提条件。

实际钻井过程中，底部钻具的强烈振动和工具随钻柱的快速旋转会对加速度计的工具姿态测量产生严重干扰，导致姿态参数失真，严重影响纠斜效果，使得井眼轨迹不可控。

文献[4]讨论了基于重力加速度计的井斜角静态和动态测量问题，其采用低通滤波器电路以滤除部分振动影响，再用Butterworth 低通数字滤波器进一步滤除残余振动和传感器自身交流噪声影响，结合转速校正，提出了工具姿态动态测量的方案并进行了实验验证[5]。但实际钻井实验发现，由于近钻头高频高幅值振动的影响，该方法姿态参数测量仍然存在较大误差，不能满足导向控制的要求。

本文研究了LMS自适应滤波方法，以消除近钻头振动对姿态参数动态测量的影响，提高姿态参数解算的精度。

1 导向工具姿态的动态测量问题

1.1 旋转运动对姿态测量的影响

在实际钻井过程中，设导向工具绕其回转中心以转速ω旋转，则重力加速度计的工作状态如图1所示，图中R为加速度计中心O′到工具回转中心O的距离。

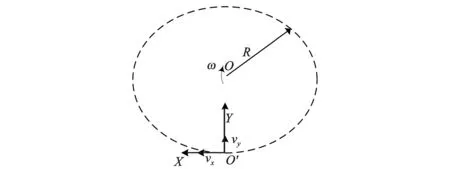
图1 旋转时的加速度计工作状态示意图Fig.1 Schematic diagram for rotating state of accelerometer

此时，X轴质量块(X轴重力加速度计等效质量)将会受到切向的附加惯性力作用，因此作用在X轴加速度计质量块的加速度ax不仅仅是重力加速度分量，还包括切向附加惯性力加速度。由加速度线性叠加原理得

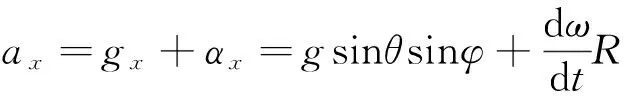
(1)

其中，gx为X轴质量块重力加速度分量，m/s2；αx为X轴质量块所受到的切向附加惯性力加速度，m/s2，它与转速ω的变化率成正比例；θ为井斜角、φ为工具面角(下同)。

Y轴重力加速度计质量块也会因旋转而受到离心力作用，其加速度

ay=gy+αy=gsinθcosφ+ω2R。

(2)

其中，gy为Y轴质量块重力加速度分量，m/s2；αy为质量块所受到的离心力加速度，m/s2，它与转速平方成正比。由式(1)、(2)可知，当工具转速较高时，安装在导向工具上的重力加速度计在井眼的不同方位上将产生差异较大的测量信号，从而导致工具姿态的较大测量误差。

1.2 近钻头振动对姿态测量的影响

在正常钻进过程中，钻头切削岩石会使钻柱产生横向和纵向振动，且横向振动尤为明显。文献[6]的实验表明：近钻头振动信号有3大特性：①牙轮钻头牙齿吃入岩石形成高频特性；②近钻头震源具有宽频性；③钻头牙齿、牙轮与钻头整体复合运动具有随机性。近钻头振动信号的幅值一般在10 g左右(g为重力加速度，9.8 m/s2)，最大可达到30 g[7]。因此，近钻头的振动加速度一般远大于重力加速度，弱小的重力加速度信号将湮灭在振动加速度噪声中，导致工具姿态测量无效。根据近钻头横向振动信号特性，采用幅值为6 g的随机白噪声来模拟近钻头高频随机振动信号，信号特征如图2所示。

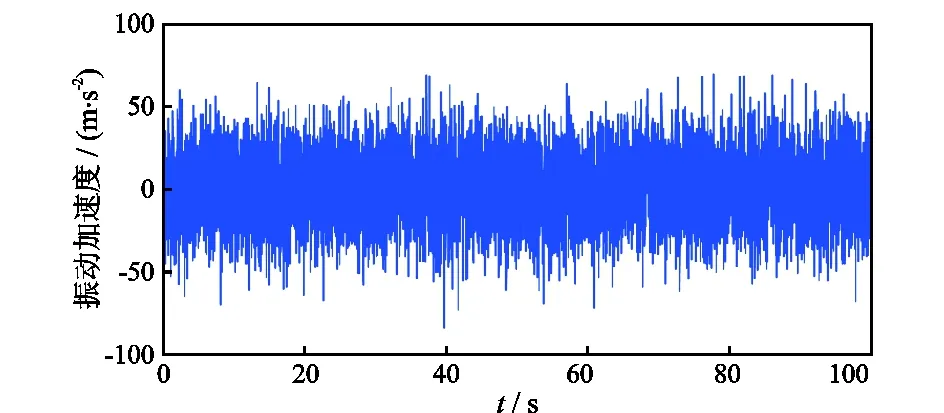
图2 近钻头振动信号模拟Fig.2 Simulation of vibration signal near bit

设仅考虑近钻头处的横向振动，其对 X、Y轴向分解后分别记为Ax、Ay，设Ax=Kxg，Ay=Kyg；Kx、Ky为最大值为10的随机系数。假设近钻头振动、旋转运动以及重力加速度对加速度计的影响线性可加，则X,Y轴重力加速度计的测量信号为

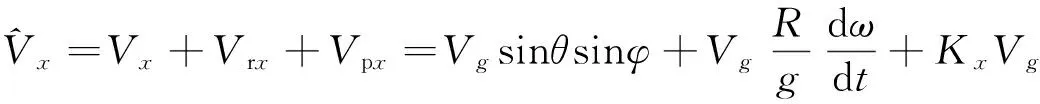
(3)

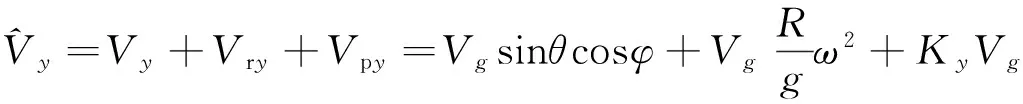
(4)

其中：Vx、Vy为加速度计的理想输出信号；Vrx、Vry分别为X、Y轴加速度计的旋转附加信号；Vpx、Vpy为振动产生的附加信号。

2 导向工具姿态动态测量方法

2.1 工具旋转转速补偿算法

考虑到工具旋转时的附加信号Vrx、Vry为转速ω的函数，因此，利用速率陀螺仪实时测出工具转速ω，则可进行误差校正。

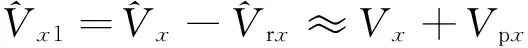
(5)

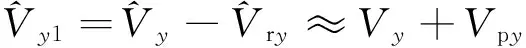
(6)

2.2 振动信号的自适应滤波

近钻头振动信号是一种宽带噪声信号，自适应滤波器利用其自动调节参数的优势，无需知道输入信号和噪声统计特性，自动跟踪噪声源，将噪声滤除。自适应滤波的基本思想是：将振动信号与滤波估计出的参考信号进行抵消操作[8]。

自适应滤波器有两路输入，一路为原始通道，其不仅接收加速度计测量信号Vx(k)(将加速度传感器测量信号离散化)，还接收和信号Vx(k)不相关的

近钻头振动附加信号Vrp0(k)。另一路为参考输入通道，其接收与信号Vx(k)不相关且与振动信号Vrp0(k)相关的振动信号Vrp1，其结构如图3所示。根据自适应滤波器的特性，振动信号Vrp1(k)经过LMS自适应滤波器[9]自动调整输出后，得到Vrp1(k)的估计信号，即

(7)

则自适应滤波器系统输出的误差信号e(k)等于原始信号和参考输入信号的差值，表示为：

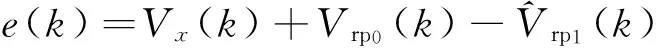
(8)

将式(8)等号左右两边做平方运算，得到

e2(k)=Vx2(k)+[Vrp0(k)-Vrp1(k)]2+2Vx(k)[Vrp(k)-Vrp1(k)]。

(9)

对式(9)取均方误差可得

E[e2(k)]=E[Vx2(k)]+E[(Vrp0(k)-Vrp1(k))2]+2E[Vx(k)(Vrp(k)-Vrp1(k))]。

(10)

式(10)中，E[e2(k)]表示功率信号，Vx(k)与Vrp1(k)无关，所以2E[Vx(k)(Vrp(k)-Vrp1(k))]=0，因此，均方误差E[e2(k)]最小，等价于E[(Vrp0(k)-Vrp1(k))2]达到最小。

LMS自适应滤波过程是由其权向量迭代公式

W(k+1)=W(k)+2μe(k)x(k)

(11)

自身调节权值W(k)使得E[e2(k)]达到最小的过程。

式中：μ为调整搜索步长的正值常数，其收敛速度与系统稳定性有关；W(k)为系统第k次迭代权系数；x(k)为输入信号。

根据式(8)，导出式：

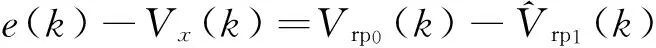
(12)

所以在LMS准则下，E[(e(k)-Vx(k))2]被最小化的同时，E[(Vrp0(k)-Vrp1(k))2]也被最小化了，即LMS自适应滤波器的输出y(k)向Vrp1(k)逼近等效于e(k)向Vx(k)逼近，从而系统输出的是加速度计信号Vx(k)的最佳估计。

图3 自适应滤波原理图Fig.3 Adaptive filtering principle diagram

3 自适应滤波的姿态测量数值仿真

3.1 数值仿真系统结构

在导向工具姿态参数静态解算方程的基础上(考虑加速度计、陀螺仪的测量误差均为5%)，加入导向工具旋转与近钻头振动信号，并将导向工具工具面角反馈到前一时刻，其仿真系统结构如图4所示。

在实际钻井过程中，工具处于不断旋转与运动状态，工具面角随工具转速而变化，因此将工具转速ω作为仿真系统的输入。给定工具旋转转速ω、近钻头振动信号，设定井斜角为θ=0.3°、初始工具面角φ0=0°，工具面角的递推计算式为

φi+1=φi+ωT。

(13)

图4 系统仿真结构图Fig.4 System simulation structure diagram

3.2 数值仿真分析

导向工具匀速旋转的条件下，工具姿态参数未进行转速补偿或滤波处理时，当井斜角θ=0.3°、工具面角φ=30°时(设重力加速度计、速率陀螺仪的测量误差均为5%)，工具姿态参数的仿真结果如图5、图6所示。

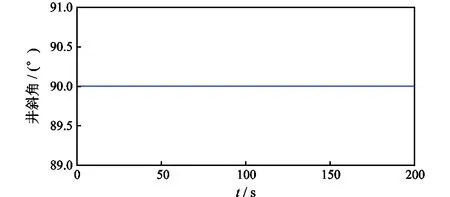
图5 θ=0.3°时井斜角未处理的仿真结果Fig.5 Simulation result of unprocessing well angle when θ=0.3°

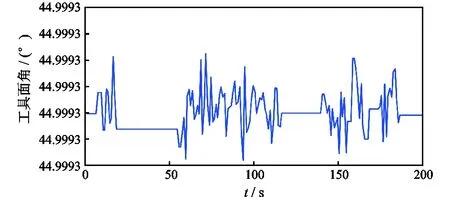
图6 φ=30°时工具面角未处理的仿真结果Fig.6 Simulation result of unprocessing tool face angle when φ=30°

3.2.1 工具匀速旋转时的姿态测量仿真 在井斜角θ=0.3°的情况下，工具以ω=(1/3)π rad/s的速率匀速旋转时的仿真结果如图7、图8所示。

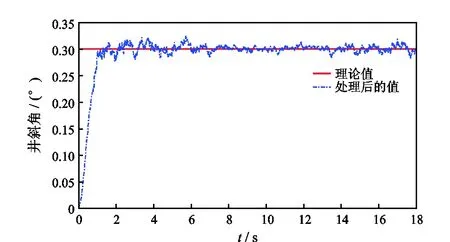
图7 ω=(1/3)π rad/s、θ=0.3°时井斜角处理后的值与理论值Fig.7 Processed well angle and theoretical value of well angle when ω=(1/3)π rad/s and θ=0.3°

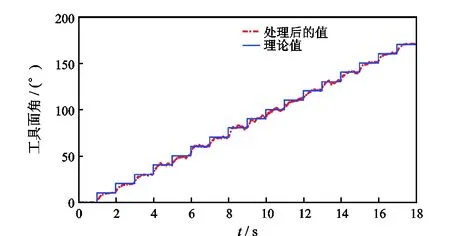
图8 ω=(1/3)π rad/s、θ=0.3°时工具面角处理后的值和理论值Fig.8 Processed tool face angle and theoretical value of tool face angle when ω=(1/3)π rad/s and θ=0.3°

当转速ω=2π rad/s、井斜角θ=0.3°时的仿真结果如图9、图10所示。

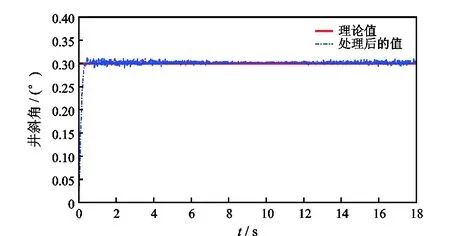
图9 ω=2π rad/s、θ=0.3°时井斜角的理论值和处理后的值Fig.9 Processed well angle and theoretical value of well angle when ω=2π rad/s and θ=0.3°

图10 ω=2π rad/s、θ=0.3°时工具面角的理论值和处理后的值Fig.10 Processed tool face angle and theoretical value of tool face angle when ω=2π rad/s and θ=0.3°

当转速ω=3π rad/s、井斜角θ=0.3°时的仿真结果如图11、图12所示。

3.2.2 工具变速旋转时的姿态测量仿真 在实际钻井过程中，导向工具转速一般为非匀速旋转。设工具非匀速旋转转速为ω=sin(0.05πt)+2π，将此转速代替工具匀速旋转时的转速，仿真结果如图13、图14所示。

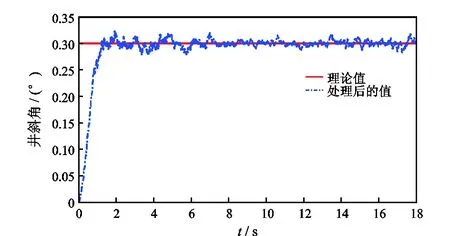
图11 ω=3π rad/s、θ=0.3°时井斜角处理后的值和理论值Fig.11 Processed well angle and theoretical value of well angle when ω=3π rad/s and θ=0.3°

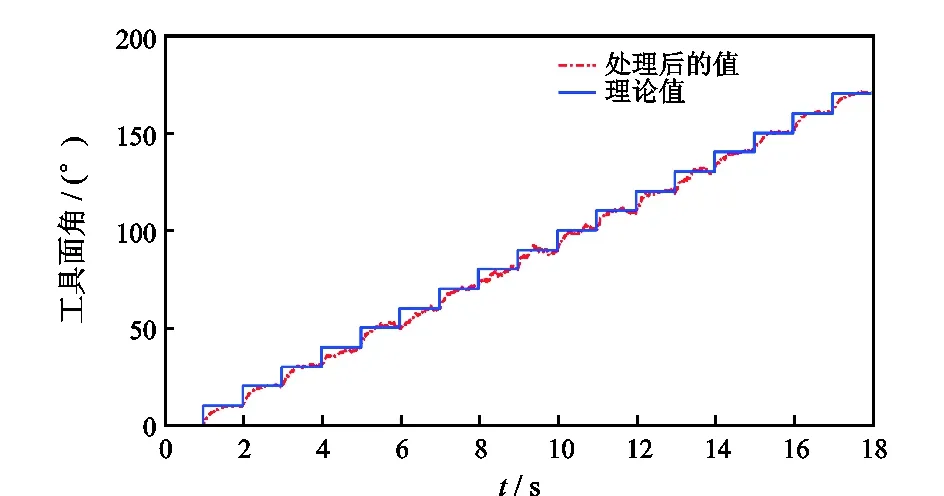
图12 ω=3π rad/s、θ=0.3°时工具面角处理后的值和理论值Fig.12 Processed tool face angle and theoretical value of tool face angle when ω=3π rad/s and θ=0.3°

图13 井斜角θ=0.3°时其理论值和处理后的值Fig.13 Processed well angle and theoretical value of well angle when θ=0.3°

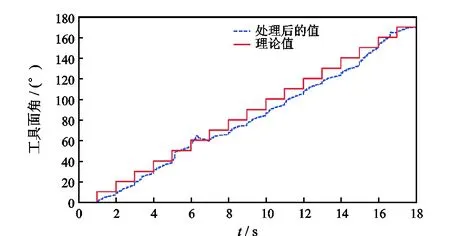
图14 井斜角θ=0.3°时工具面角理论值和处理后的值Fig.14 Processed tool face angle and theoretical value of tool face angle when θ=0.3°

由仿真结果可知，自适应滤波器大大改善了导向工具姿态参数测量精度。当工具匀速旋转时，工具转速在(1/3)π rad/s和3π rad/s时的测量误差较2π rad/s时的大，ω=2π rad/s时，井斜角测量误差小于0.01°，工具面角的测量误差小于1°；当工具转速为变量时，其井斜角最大测量误差为0.1°，工具面角最大测量误差为6°，较匀速旋转时的误差偏大。大量仿真结果表明，在工具匀速或变速旋转条件下，基于转速补偿方法与LMS自适应滤波方法的工具姿态参数均满足测量精度要求，且其改善测量性能的效果显著。

4 结 论

(1)LMS自适应滤波器可以有效滤除近钻头振动信号，用于工具姿态参数的动态测量时，改善测量性能效果显著。

(2)转速补偿方法可以有效解决导向工具在旋转工作模式下的姿态测量问题。当导向工具匀速旋转时，补偿后的工具面角最大测量误差不超过1°；工具变速旋转时，其最大测量误差不超过6°。

(3)转速补偿与LMS自适应滤波器结合，能够有效解决工具姿态参数的动态测量问题。经过转速补偿和LMS自适应滤波后，井斜角测量误差可小于0.1°，工具面角测量误差小于6°，有效地提高了垂直导向钻井工具的动态测量精度。

[1] 张绍槐.现代导向钻井技术的新进展及发展方向[J].石油学报，2003,24(3)：82-85. ZHANG Shaohuai.New progress and development direction of modern steering drilling techniques[J].Acta Petrolei Sinica,2003,24(3):82-85.

[2] 汤楠，霍爱清，汪跃龙，等.旋转导向钻井稳定平台控制对象动态特性研究[J].石油学报，2009,30(4)：598-602. TANG Nan,HUO Aiqing,WANG Yuelong,et al.Study on dynamic characteristics of controlled objects in stabilized platform of rotary steerable drilling system[J].Acta Petrolei Sinica,2009,30(4):598-602.

[3] 汪跃龙，张璐，汤楠，等.旋转导向钻井惯导平台动力学分析与运动研究[J].机械工程学报，2012,48(17)：65-69. WANG Yuelong,ZHANG Lu,TANG Nan,et al.Dynamics and rotational movement analysis of servo platform for rotary steerable drilling system[J].Journal of Mechanical Engineering,2012,48(17):65-69.

[4] 刘白雁，苏义脑，陈新元，等.自动垂直钻井中井斜动态测量理论与实验研究[J].石油学报，2006,27(4)：105-109. LIU Baiyan,SU Yinao,CHEN Xinyuan,et al.Theoretical and experimental investigation on dynamic measurements of hole inclination in automatic vertical drilling process[J].Acta Petrolei Sinica,2006,27(4):105-109.

[5] 龚勋，刘白雁，陈新元，等.自动垂直钻井工具纠斜控制实验研究[J].石油钻采工艺，2009,31(4)：16-20. GONG Xun,LIU Baiyan,CHEN Xinyuan,et al.Experimental study on automatic vertical drilling tool inclination control[J].Oil Drilling & Production Technology,2009,31(4):16-20.

[6] 宿雪.钻柱振动信号测量及处理技术研究[D].东营：中国石油大学(华东),2010.

[7] 祝效华，胡志强.基于钻头破岩钻进的下部钻具横向振动特性研究[J].振动与冲击，2014,33(17)：90-93. ZHU Xiaohua,HU Zhiqiang.Lateral vibration characteristics analysis of a bottom hole assembly based on interaction between bit and rock[J].Journal of Vibration and Shock,2014,33(17):90-93.

[8] HUNG Wei Chiu.A2.17-dB NF 5-GHz-Band monolithic CMOS LNA with 10 mV DC power consumption[J].IEEE Trans Mocroware Theo,2005,53(3):813-824.

[9] BISMOR Dariusz.LMS algorithm stemp size adjustment for fast convergence[J].Archives of Acoustics,2012,37(1):31-40.

责任编辑：董 瑾

Adaptive Filtering Method for Dynamic Measurement of Steering Drilling Tool Attitude

HE Yan1,2,WANG Yuelong1,GAO Yi1,WANG Tong1,LI Yudan1

(1.College of Electronic Engineering,Xi'an Shiyou University,Xi'an 710065,Shaanxi,China;2.Shaanxi Electronic Technology College,Xi'an 710125,Shaanxi,China)

Under drilling condition,the vertical steering drilling tool is in the state of vibration and rotation,and the dynamic measurement accuracy of tool attitude parameters is low.Through theoretical analysis and numerical simulation,the speed compensation algorithm is proposed to eliminate the influence of tool rotation on the measurement.And the influence of bit vibration on the measurement of tool attitude parameters can be effectively eliminated by least mean square (LMS) adaptive filtering algorithm.The numerical simulation results show that after the speed compensation and LMS adaptive filtering,the measurement error of deviation angle can be less than 0.1°,and the measurement error of tool face angle is less than 6°.The speed compensation and LMS adaptive filtering can effectively improve the dynamic measurement precision of vertical steering drilling tool.

steering drilling tool;dynamic attitude measurement;LMS algorithm;adaptive filter

2016-03-02

国家自然科学基金(编号：51604226)；陕西省教育厅重点实验室科研计划项目(编号：16JS090)

贺艳(1990-)，女，硕士研究生，主要从事垂直导向钻井工具研究。E-mail:1210015163@qq.com.com

10.3969/j.issn.1673-064X.2016.06.017

TE921.2

1673-064X(2016)06-0108-06

A