移动用户下一地点预测新方法

马春来, 单 洪, 李 志, 朱立新

(解放军电子工程学院,安徽 合肥 230037)



移动用户下一地点预测新方法

马春来, 单 洪, 李 志, 朱立新

(解放军电子工程学院,安徽 合肥 230037)

针对目前移动用户地点预测方法对时间的依赖性较强且在小数据集上表现差的问题,提出一种基于皮特曼-尤尔及移动马尔可夫链(PY-MMC)模型的下一步地点预测方法.该方法综合考虑目标用户轨迹的短时效应及幂律分布特征.以用户的时间位置熵为参考,计算可预测性因子.依据该因子对皮特曼-尤尔模型及移动马尔可夫链模型输出的概率线性加权,建立PY-MMC模型.利用新模型计算每个下一步候选地点的概率,并取最大者输出,完成下一步地点的预测.以“Geolife”及“Foursquare”数据集为例,采用一步准确率、一步候选准确率及平均准确率3个评估指标进行实验.结果表明：新方法能够有效克服基于MMC模型的预测方法准确率随时间波动较大的不足.同时,该方法解决了基于PY模型的预测方法对子序列长度过度依赖的问题.

移动马尔可夫链(MMC); 皮特曼-尤尔过程; 位置熵；移动用户；下一地点预测

基于位置的服务(location based services,LBS)的普及与机器学习、数据挖掘等技术的发展,使得位置大数据(location big data, LBD)的价值提取成为一个新兴、热点问题[1].研究表明,在获取移动用户历史位置信息的情况下,通过时空挖掘技术,不仅能够有效推断用户的家庭住址、工作地点[2],还能够对用户的位置进行预测[3].在商业层面,位置预测可以用于基于位置的推荐系统[4],如根据用户可能到达的地方,推荐用户所需的服务、新的朋友、多媒体信息等；在公共安全层面,位置预测可以用于对目标用户进行跟踪定位,掌握其预定轨迹[5],有效防范危害公共安全事件的发生[6-7].由此可见,研究位置预测对于LBS中的隐私保护及位置大数据的价值提取具有重要意义.

目前,位置预测的方法主要分为3类.1)以用户个体移动的特征或属性为依据进行建模并预测,如利用用户签到的幂律分布属性,建立HPY(hierarchical Pitman-Yor)模型进行预测[8].利用用户活动规律的周期性,建立周期移动模型进行预测[9].利用用户轨迹的短时效应,建立n-MMC模型进行预测[10-11]等.2)利用机器学习方法进行预测,如动态贝叶斯网络[12]、人工神经网络[6]等方法.但这些方法需要进行训练学习,时间及空间代价较大.3)以第三方信息(如：社会关系、地点类别、移动距离、人员类型、轨迹相似性)为辅助进行预测[13].这类方法需要额外的先验知识作输入,部分数据集无法满足该要求.

基于用户个体移动特征建模的方法,能够从目标个体的移动本质出发,预测用户的轨迹,具有较高的预测效率和准确率.然而,以上方法所用模型仅基于用户轨迹的某一属性,并未将多种属性综合考虑.鉴于此,本文将以目标个体轨迹的短时效应和幂律分布特征为依据,将移动马尔可夫链(mobility Markov chain， MMC)和Pitman-Yor过程结合起来,提出一种基于PY-MMC模型的位置预测方法,完成对目标用户下一步地点的预测.

1 问题描述

设数据集

D={d1,d2, …,dW}.

式中：di=(ui,ti,φi),i=1,2,…,W,ui为用户ID,ti为用户到访时间,φi为用户到访地点的经纬度.选取某一用户为研究对象.首先进行预处理(剪枝、聚类)[14]及兴趣点(points of interest,POI)识别[15].然后提取出轨迹集Τ={(ti,li)|i=1,2,…,X}、时间序列t=(t1,t2,…,tX)、位置序列L=(l1,l2, …,lX).其中,X为用户轨迹总长度,li∈Q.Q={qj|j=1,2 …,RL}为用户ui到访过的POI或簇标号集合,RL为用户曾到过的地点的集合大小.地点流程图反映了各数据集与变量的关系,如图1所示.

图1 移动用户地点预测流程图Fig.1 Flow chart of next place prediction of mobile users

结合图1,地点预测问题可描述如下：设ui为目标用户,已知T为该用户的轨迹集(长度为X),给出该用户下一步地点lX+1的条件概率分布P(lX+1|T).

2 短时效应与MMC模型

2.1 短时效应

用户个体具有一定移动转移性,这种转移性建立了用户当前位置与此前一个时间段τ内的轨迹关联关系.设该轨迹序列为L′,其中,L′=(l1,l2,…,lY).下一步地点为qi的概率可表示为序列(L′,qi)在序列L中出现的比例,如下式所示：

(1)

(2)

2.2 MMC模型

传统的马尔可夫链虽然在一定程度上能够描述用户活动的短时效应,但并未考虑周视图及日视图下用户活动规律的差异性.例如：一天之中不同时间段用户的移动规律不同,一周之中每一天用户的移动规律也不尽相同.传统马尔可夫链忽视了这种差异性,降低了其地点预测的精度.MMC模型将某一时间段w作为窗口,首先在局部考察时间窗口内部的状态转移情况,然后在全局考察不同窗口之间的状态转移情况.MMC生成算法如下所示.

输入：数据集D、时间段数目m、稳态分布初始值λ0

输出：Mw、Mg、Iw、Ig

1) 将地点或簇标注为不同的POI_ID，并生成轨迹序列Τ(若数据集D为GPS数据等连续轨迹则需要进行剪枝、聚类等预处理).

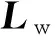
4) 计算时间窗口之间的状态转移矩阵Mg、稳态分布的特征向量λg及行号索引矩阵Ig并输出.

Iw及Ig分别为Mw及Mg的行号索引矩阵,存放L′与转移矩阵的对应关系.在利用训练数据生成MMC模型后,根据已知轨迹进行预测,算法如下所示.

输入：Mw、Mg、Iw、Ig

输出：Next_ID、PMMC

1) 根据L′及Iw、Ig,按行搜索Mw、Mg的行号.

2) 根据获取的行号,搜索本行最大值MaxValue.

3) 若有且仅有一个非零最大值,将MaxValue输出为PMMC,该MaxValue对应的列号输出为Next_ID.

4) 若该行有多个MaxValue,则随机选择1个,将其输出为PMMC,将其对应的列号输出为Next_ID.

5) 若该行均为0,则Next_ID及PMMC输出均为0.

MMC模型虽然能够较好地考虑到不同时间窗口用户行为的差异性,但并未从统计意义上对用户概率分布进行分析，因此，MMC模型在分析较长位置序列时具有一定局限性.

3 幂律分布与Pitman-Yor过程

3.1 幂律分布

文献[3]指出,在一段时间内,用户到访地点的频次与该频次的概率密度呈幂律分布[16].将用户到访地点频次的概率降序排列后,频次概率密度pf的对数与频次f的对数呈线性关系,如下式所示：

lnpf=-αlnf+c.

(3)

式中：α及c均为常数.对式(3)两侧同时作指数运算可得

pf=Cf-α.

(4)

式中：C=exp (c)亦为常数.

下式为其累积分布可表示为用户到访频次大于或等于f的点集所占比例：

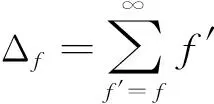
(5)

由式(5)可推得

(6)

为验证用户历史轨迹的幂律分布属性,以“Geolife”数据集为例进行实验.采用速度剪枝及基于密度的聚类算法(本文采用CFSFDP(clustering by fast search and find of density peaks)算法[17])将无关噪声点剔除,分别统计85名用户到访各簇的频次,给出对数坐标轴下用户到访频次的累积分布如图2所示.由图2可以看出,在对数坐标轴视图下,用户的到访频次概率分布与到访频次均呈线性关系.这也验证了用户到访频次基本服从幂律分布的特征.

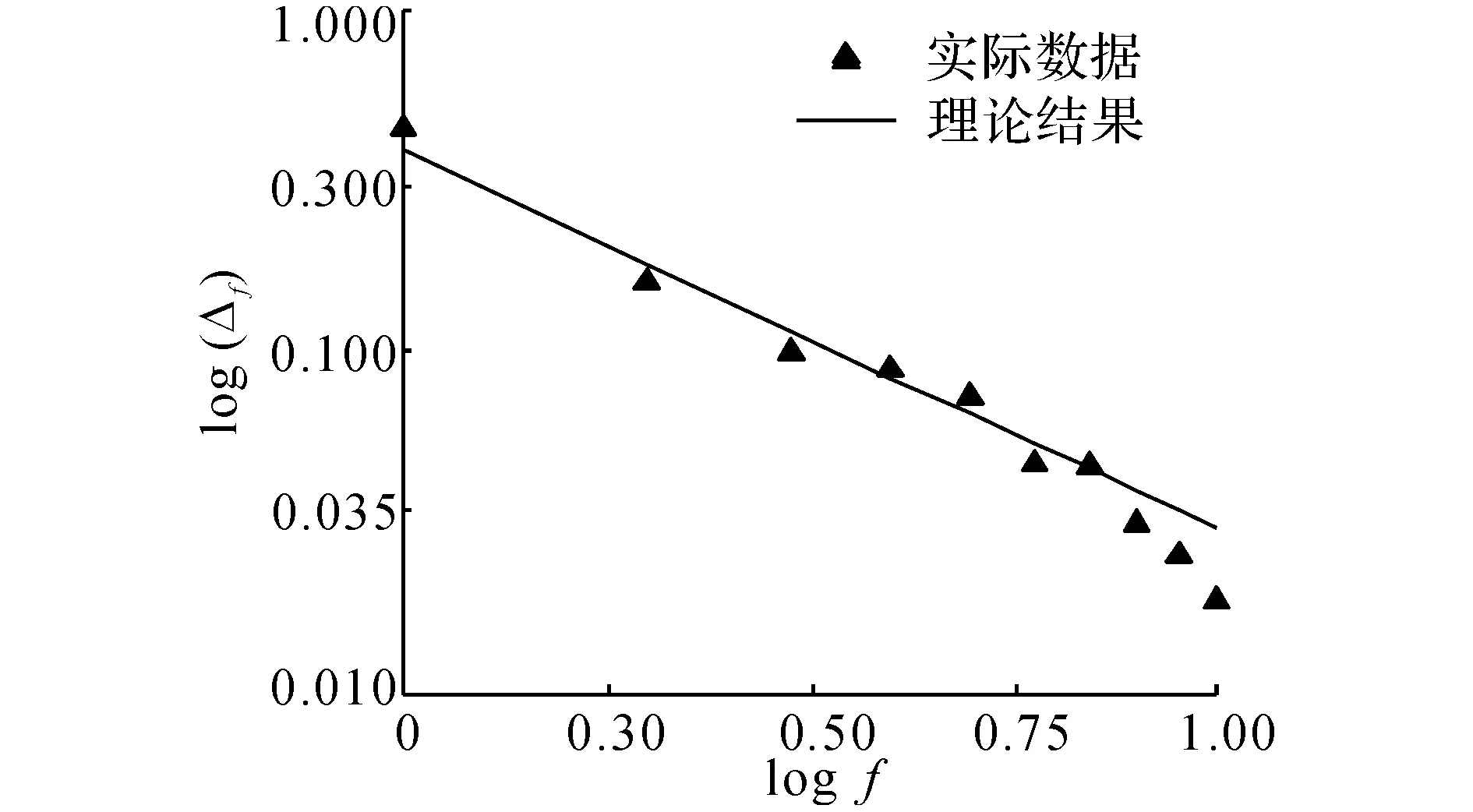
图2 用户到访频次与累积分布的关系Fig.2 Correlation between user’s check-in frequency and cumulative distribution function

3.2 Pitman-Yor过程

幂律分布有多种描述方法,其中自然语言处理中的词分布服从幂律分布,其层次结构又与用户到访地点结构极为相似.鉴于该相似性,可通过类比思想将自然语言处理中的方法应用到对用户移动规律的描述上来.目前较为经典的语言模型为Pitman-Yor过程[18].该过程能够准确描述Power-law分布：

G～ζ(d,γ,G0).

(7)

用该过程类比描述轨迹模型,则G可表示下一次目标用户到访地点的分布,ζ表示Pitman-Yor过程,γ及d∈[0,1)为控制Power-law属性的参数,若d=0则Pitman-Yor过程退化为Dirichlet过程.初始分布G0(l)=1/RL表示目标用户签到的先验概率.

考虑到L为用户数据规模,若其时间跨度较长,则在此期间用户的活动区域及移动规律有可能发生迁移,从而影响对用户移动模式的预测.因此,从序列L中选择最近一段子序列L″作为位置预测的参考数据.若L数据的时间跨度较小或其规模不大,则L″默认取整段L.在已知序列L″的条件下,用户下一步出现的位置坐标φZ+1可能以现有分布隶属于已有POI集Q,也可能是以一个新的分布形式包含于某一地点qi.用户下一次到访地点概率可分为两部分.若到访地点为qi,则其概率可表示为

(8)

式中：Pexit为到访新地点的概率，Pnew为到访已存在地点的概率,Ni表示用户到访第i个POIqi的总数目,

为签到序列的长度,RL″表示序列L″中用户到访过的不同POI的数目.

在确定模型参数后,即可通过Pitman-Yor模型计算每一个可能到访的地点的概率,选取最大值及对应的POI标号,完成用户位置预测.

4 PY-MMC模型

4.1 模型定义

MMC模型在进行位置预测时,考虑了最近一段轨迹的序列关系,能够较好地描述短时效应,但存在以下缺点.1)仅根据局部轨迹信息进行预测,无法从统计意义上描述用户到访地点的分布.2)仅根据曾出现的序列生成转移矩阵,遇到未出现过的序列时,无法进行预测.3)在用户活动频繁但又到访地点较多的区域,预测准确度较差.Pitman-Yor过程采用非参数贝叶斯进行估计,使模型能够较好地适应数据集的变化,从而较好地描述用户移动的幂律分布特性,但该方法忽略了地点之间的前后继承关系.

鉴于此,本文将Pitman-Yor过程及MMC模型结合,提出一种PY-MMC模型.该模型同时考虑了用户个体在移动过程中呈现的短时效应及幂律分布特性.MMC考虑的仅为时间窗口w内用户到访过的地点序列,但用户在每个窗口w内的活动规律不尽相同.研究表明,用户在夜间的移动性更差,在工作日的移动性更具规律性,而在休息日的移动性则更加随机.用户移动的随机性越强,可预测性就越差,MMC模型预测的准确率就越差,这就意味着在时间窗口w中,MMC模型预测的可信度与用户的不确定性负相关.因此,PY-MMC模型采用可预测性因子作为MMC输出可信度的权值,定义如下式所示：

(9)

式中：η为可预测性因子,μ为调节因子,用于调节η的影响程度,使权值的变化在[(1-μ)/2, (1+μ)/2 ].由此可以看出,已知位置序列L预测下一步地点在qi的概率由PMMC及PPY加权计算而得.在计算P(qi|L)之后,选择最大概率输出,并得到用户在已知轨迹Τ条件下的下一步地点.具体算法如下所示.

输入：Τ、m、μ、w

输出：Next_ID、PPY-MMC

1) 根据前述第一个算法,生成MMC,得到相应的Mw、Mg、Iw、Ig.

2) 根据Mw、Mg、Iw、Ig,计算用户j下一步可能到达的每一个地点qi的概率PMMC.

3) 根据式(8),计算用户j下一步可能到达的每一个地点qi的概率PPY.

4) 根据式(9),计算用户j下一步可能到达的每一个地点qi的概率PPY-MMC.

5) 若有且仅有一个非零最大值,将最大值MaxValue输出为PPY-MMC,该MaxValue对应的列号输出为Next_ID.

6) 若该行有多个MaxValue,则随机选择1个,将其输出为PPY-MMC,并将其对应的列号输出为Next_ID.

7) 若该行均为0,则Next_ID及PPY-MMC输出均为0.

由此可见,PY-MMC模型并不是PY模型和MMC模型输出概率的简单相加,而是根据可预测性因子作为权重分布的重要参考,下面将给出该权值的度量方法.

4.2 可预测性因子定义

由于熵能够对事件发生的不确定性进行量化,从空间及时间的角度,都可以对时空信息的不确定性进行描述.将位置熵分为空间位置熵和时间位置熵,空间位置熵表征的是不同用户到访某一地点的不确定性,反映了该地点的多样性,用于区分地点的属性(公共场所、居住区域).时间位置熵能够表示用户在某一时段移动的不确定性,用于描述用户的活跃性和可预测性.参照文献[19]定义用户在某一时间窗口内的时间位置熵(简称时位置熵)：

(10)

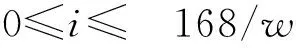
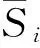
图3 不同时间窗口下用户时位置熵与时间关系Fig.3 Correlation between user’s location entropy and time with different time windows

不同时间窗口用户平均时位置熵的明显差异性说明了不同时间段用户具有不同的可预测性,故本文采用时位置熵表征可预测性因子：

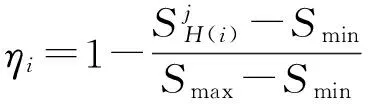
(11)

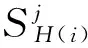
5 实验与结果分析

5.1 实验准备

为检验所提出模型的有效性,本文选取了连续更新的GPS轨迹和偶发更新的LBSN(location based social network)用户Check-in数据中的具有代表性的公开数据集：Geolife数据集[20]和Foursquare数据集[8].

Geolife为微软亚洲研究院的公开项目,该项目采用GPS接收机每5 s跟踪并采集了182个用户的自2007年4月至2012年8月的移动轨迹.该数据集共分两个版本,具体参数如表1所示,其中,NU为用户数量,NT为轨迹数量,NL为位置数量，Dt为用户总的移动距离.

表1 “Geolife”数据集的基本属性

Foursquare是于2009年诞生的基于位置服务的社交网站,截至目前,约有4 500万用户.如表2所示为通过公开应用程序接口(application program interface,API)爬取到的用户签到数据.其中,NF为用户之间相互关注的数量.

表2 “Foursquare”数据集基本属性

分别从Geolife及Foursquare数据集中提取85名、70名用户的轨迹,进行如下实验.1)研究PY-MMC模型的阶数对下一步地点预测准确率的影响,在验证模型的有效性的同时,给出合适的N的参考值.2)研究序列L″的长度Z对模型预测方法的准确率的影响,进一步验证该预测方法的有效性.3)分别采用MMC模型、PY模型及PY-MMC模型进行对比实验,考察3种方法准确率与数据集序列长度X之间的关系.4)采用多个用户的多条轨迹进行实验,统计并对比新模型与MMC、PY模型的预测准确率.5)在周视图下,考察3种方法在不同的时间窗口中的位置预测准确率.

实验共分为3个步骤：1)对目标用户的数据集进行速度剪枝处理,并剔除噪声点；2)采用基于密度的聚类方法对处理过的数据集进行聚类,并对每个簇标号,生成用户轨迹数据集T；3)根据不同模型的初始参数值,从T中选取序列L、L′、L″进行预测,并以L后的地点作为参考,统计预测准确率.

本文采用以下3种评估指标对预测准确率进行度量：

1)一步准确率：用户下一步地点预测正确的次数Nstep与该用户轨迹总数目Ntraj之比：

(12)

2)一步候选准确率：用户下一步地点在候选列表Lk中的次数Ncand与该用户轨迹总数目Ntraj之比：

(13)

式中：Ncand为用户下一步地点预测正确的次数,Ntraj为参与预测的轨迹总数目.本次实验中候选列表Lk长度k=3.

3)平均准确率：多名用户下一步地点预测正确的次数之和与轨迹总数目之比：

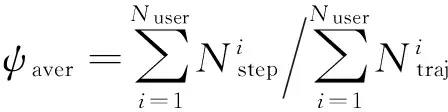
(14)

5.2 实验结果分析

1)模型预测准确率与PY-MMC阶数Y之间关系实验.

取数据集长度X=260,时间段数目m=3,子序列长度Z=260,强度参数γ=5,减损参数d=0.5,调节因子μ=0.6选取不同的MMC阶数(Y=1, 2, 3, 4),考察PY-MMC预测准确率σ如图4所示.

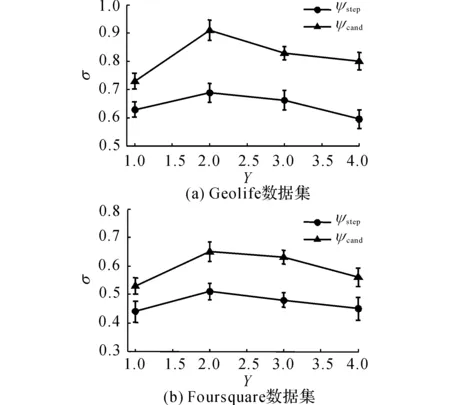
图4 皮特曼尤尔-移动马尔可夫链模型-阶数与准确率的关系Fig.4 Correlation between accuracy and order of PY-MMC model

由图4(a)、4(b)可看出,随着阶数Y的增加,模型一步准确率和候选准确率先升高后降低,在Y=2时,PY-MMC预测准确率最高.这说明了目标用户下一步地点与包括当前地点在内的前2个地点密切相关.分析原因如下：当Y<2时,下一个状态仅与当前状态有关,在进行预测时没有考虑到序列关系,从而使生成的转移矩阵过于单一,导致预测准确率降低；当Y>2时,较早的状态参与了对下一个状态的预测,而这些状态往往过于冗余,形成的转移矩阵也较为庞大,降低了马尔可夫链的泛化能力,增加了预测误差.

2)模型预测准确率与PY-MMC模型子序列长度Z之间关系实验.

图5 皮特曼尤尔-移动马尔可夫链模型中子序列长度与准确率的关系Fig.5 Correlation between accuracy and length of sub-sequences of PY-MMC model

分别选取不同的子序列L″,采用PY-MMC模型进行预测,考察预测准确率(见图5).由图5(a)、5(b)可以看出,随着子序列长度Z的增加,模型预测准确率呈上升趋势.当Z≥270时,预测精度基本不再变化.这是由于PY-MMC模型中的子模型依据Pitman-Yor过程,而这一过程及幂律分布需要较多的点来表征.在子序列长度Z增加时,更多的位置点参与了对该分布的描述,从而使模型的预测准确率逐渐增加.

3)三种模型预测准确率与数据集大小X之间关系实验.

图6 不同数据集大小条件下PY, MMC and PY-MMC模型准确率Fig.6 Accuracies of PY, MMC and PY-MMC model with different dataset sizes

通过分段选取130个不同长度的轨迹集,其长度X=50n(n=1,2,…,10),考察X取不同值时模型准确率的变化情况.由图6(a)、6(b)可以看出,随着数据集长度增加,三种模型的预测准确率均先逐渐增加后趋于平缓.这说明了无论何种模型,都需要充足的训练集来训练,才能保证有较稳定的预测准确率.另外,在X较大时,PY-MMC模型准确率略高,而PY与MMC的准确率基本一致.在X较小时,MMC及PY-MMC模型的准确率均明显高于PY模型的准确率.这说明了PY模型由于无法用较少的数据得到更为精确的分布,从而难以应用于长度较短的数据集中.

4)三种模型预测准确率与时间窗口w关系实验.

图7 不同时间窗口条件下PY、MMC、PY-MMC模型的准确率对比Fig.7 Accuracy comparison of PY, MMC and PY-MMC model with different time windows

以w=8为时间窗口,将一周分为21个时间窗,统计每一个窗口内3种模型的预测准确率,如图7所示.由图7(a)、7(b)可看出,相比于PY及PY-MMC模型,MMC模型的预测误差波动较为明显.在每一天的第1、3个窗口MMC均具有较高的准确率,而在第2个时间窗口MMC的预测误差较大.这主要是由于MMC模型仅根据较短的序列进行预测,其预测准确率受时间窗内的不确定性影响较大,而用户在不同的时间窗口移动的不确定性不同,这就导致了MMC的不稳定.相比于MMC及PY-MMC模型,PY模型的预测误差较为平稳,基本与时间无关.尤其在第16～21个时间窗口(周六、周日)内,这种差别更为明显.这主要是由于PY模型仅描述的是子序列内各数据点的分布过程,不包含时间标签,在不同的时间窗口表现都是一致的.

5)三种模型平均准确率统计对比.

为综合考察3种模型的表现,对85名用户不同长度的轨迹进行预测,统计其预测准确率均值.如表3所示.

表3 PY、MMC、PY-MMC模型预测平均准确率

Tab.3 Average accuracies of PY, MMC and PY-MMC model for prediction

%

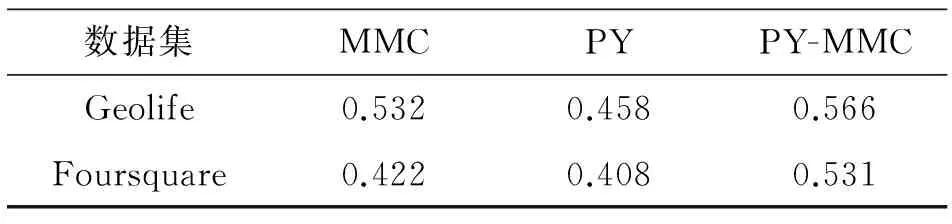
由图4～7及表3可以看出,相比于Geolife,Foursquare数据集准确率较低.这主要是由于偶发更新的轨迹数据与LBSN用户签到习惯有关,稀疏的数据造成了较多细节信息的缺失,从而导致无法获得更高的准确率.无论是对于Geolife数据集是Foursquare数据集,相比于PY及MMC模型,PY-MMC模型在不同的数据集长度、不同的时间窗口、不同的用户的条件下均具有较高准确率.这主要是由于PY-MMC模型同时考虑了PY模型及MMC模型的优点,兼顾了用户轨迹的短时效应和幂律分布特征.该模型既能解决PY模型因数据量不足而难以描述幂律分布的问题,又能弥补MMC模型的预测准确率随时间变化较大的缺点.

综上所述,得出以下结论：1)MMC预测准确率与阶数Y有关,Y过大或过小均会降低MMC预测准确率.2)PY预测准确率依赖子序列长度Z,较长的Z可以得到更稳定的预测.3)足够的数据集能够保证3种模型得到更准确的预测.4)MMC在不同的时间窗口,预测准确率误差波动较大.5)PY-MMC模型比MMC及PY模型更加稳定.6)数据更新越频繁,轨迹在时间尺度上越“紧密”,用户位置可预测性越强,准确率越高.

6 结 语

该模型从时间的角度将用户轨迹视为马尔可夫过程,从空间的角度将用户轨迹视为Pitman-Yor过程,从而克服了单一模型各自的缺点.实验考察了MMC阶数、子序列长度、数据集大小及不同时间窗口与模型准确率之间的关系.结果表明,相比于PY和MMC模型,PY-MMC模型在不同的数据集长度及的时间窗口条件下具有较高的预测准确率,对LBS用户的位置预测具有一定参考意义.今后将在此基础上进一步研究第三方信息(如：社会关系、POI类型)辅助下的移动用户地点预测方法.

[1] 郭迟,刘经南,方媛,等.位置大数据的价值提取与协同挖掘方法[J].软件学报,2014,25(4): 713-730. GUO Chi, LIU Jing-nan, FANG Yuan, et al. Value extraction and collaborative mining methods for location big data [J]. Ruan Jian Xue Bao/Journal of Software, 2014, 25(4):713-730.

[2] KRUMM J. Inference attacks on location tracks [J]. IEEE Pervasive Computing, 2007,4480: 127-143.

[3] LU X, WETTER E, BHARTI N, et al. Approaching the limit of predictability in human mobility [J]. Scientific Reports, 2013, 3(10): 1-9.

[4] BAO J, ZHENG Y, WILKIE D, et al. Recommendations in location-based social networks: a survey [J]. GeoInformatica, 2015, 19(3): 525-565.

[5] MIGUEL P C, FRIGNAL J. Geo-location inference attacks: from modeling to privacy risk assessment [C]∥ 2014 Tenth European Dependable Computing Conference (EDCC). Tyne: IEEE, 2014: 222-225.

[6] GUNDUZ S, YAVANOGLU U, SAGIROGLU S. Predicting next location of twitter users for surveillance [C]∥ 2013 12th International Conference on Machine Learning and Applications (ICMLA). Miami: IEEE, 2013: 267-273.

[7] BOGOMOLOV A, LEPRI B, STAIANO J, et al. Once upon a crime: towards crime prediction from demographics and mobile data [C]∥ Proceedings of the 16th International Conference on Multimodal Interaction. Istanbul: ACM, 2014: 1-10.

[8] GAO H, TANG J, LIU H. Exploring social-historical ties on location-based social networks [C] ∥ The 6th International AAAI Conference on Weblogs and Social Media. Dublin: AAAI, 2012: 1-8.

[9] CHO E, MYERS S A, LESKOVEC J. Friendship and mobility: user movement in location-based social networks [C] ∥ Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM, 2011: 1-9.

[10] CHEN M, YU X, LIU Y. Mining moving patterns for predicting next location[J]. Information Systems, 2015, 54: 156-168.

[11] GAMBS S, KILLIJIAN M, MIGUEL P C. De-anonymization attack on geolocated data [J]. Journal of Computer and System Sciences, 2014, 80(8): 1597-1614.

[12] DASH M, KEE K K, GOMES J B, et al. Next place prediction by understanding mobility patterns [C]∥ 2015 IEEE International Conference on Pervasive Computing and Communication Workshops. St.Louis: IEEE,2015: 469-474.

[13] BAUMANN P, KLEIMINGER W, SANTINI S. The influence of temporal and spatial features on the performance of next-place prediction algorithms [C]∥ Proceedings of the 2013 ACM International Joint Conference On Pervasive And Ubiquitous Computing.Zurich: ACM, 2013: 1-10.

[14] 丰江帆,熊雨虹.一种基于个人位置信息的重要地点识别方法[J].小型微型计算机系统,2013,34(3): 503-507. FENG Jiang-fan, XIONG Yu-hong. An important place identification algorithm based on personal GPS location [J]. Journal of Chinese Computer Systems, 2013, 34(3): 503-507.

[15] 王明,胡庆武,李清泉,等.基于位置签到数据的城市分层地标提取[J].计算机学报.2016,39(2): 405-413. WANG Ming, HU Qing-wu, LI Qing-quan, et al. Extracting hierarchical landmark from check-in data [J]. Chinese Journal of Computers, 2016, 39(2):405-413.

[16] CLAUSET A, SHALIZI C R, NEWMAN M E. Power-law distributions in empirical data [J]. SIAM Review, 2009, 51(4): 661-703.

[17] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks [J]. Science, 2014, 344(6191): 1492-1496.

[18] TEH Y W. A hierarchical Bayesian language model based on Pitman-Yor processes [C]∥ Proceedings of the 21st International Conference on Computational Linguistics and the 44th annual meeting of the Association for Computational Linguistics. Stroudsburg: ACM, 2006: 985-992.

[19] SONG C, QU Z, BLUMM N, et al. Limits of predictability in human mobility [J]. Science, 2010, 327(5968): 1018-1021.

[20] ZHENG Y, CHEN Y, XIE X, et al. Geolife2.0: A location-based social networking service [C] ∥ 2009 Tenth International Conference on Mobile Data Management: Systems, Services and Middleware. Taipei: IEEE, 2009: 357-358.

New next place prediction method for mobile users

MA Chun-lai, SHAN Hong, LI Zhi, ZHU Li-xin

(ElectronicEngineeringInstituteofPLA,Hefei230037,China)

A next place prediction method based on Pitman-Yor model and mobility Markov chain(PY-MMC) model was proposed to solve the problems that mobile users’ next place prediction method depended on time heavily and the performance was poor on small dataset. The method considered both short effect and power-law distribution features of users’ trajectories. The predictability factor was calculated with temporal location entropy of users. A PY-MMC model was constructed depending on the predictability factor, which was used to weight the output probability from PY-MMC model. The maximum probability of each candidate next place was calculated with the new model. Geolife and Foursquare dataset were used in experiment, which was evaluated with one-step accuracy, one-step accuracy of candidate places and average accuracy. Experimental results show that the new method can improve stability of MMC model, and solve the problem that accuracy rate of PY model based method excessively relied on the length of sub-sequence.

mobility Markov chain (MMC); Pitman-Yor process; location entropy; mobile users; next place prediction

2015-12-15.

马春来(1989—)，男，博士生，从事网络安全、情报挖掘研究. ORCID: 0000-0002-8432-2052. E-mail: eviiive@163.com 通信联系人：单洪，男，教授，博导. ORCID: 0000-0002-9669-0215. E-mail: hshan222@sina.com

10.3785/j.issn.1008-973X.2016.12.018

TP 309

A

1008-973X(2016)12-2371-09