基于贝叶斯网络云模型的目标毁伤评估方法

曲婉嘉， 徐忠林， 张柏林， 刘颖

(1.空军航空大学， 吉林 长春 130022； 2.94810部队， 江苏 南京 211500)



基于贝叶斯网络云模型的目标毁伤评估方法

曲婉嘉1， 徐忠林1， 张柏林2， 刘颖1

(1.空军航空大学， 吉林 长春 130022； 2.94810部队， 江苏 南京 211500)

针对复杂的现代战场环境和较多不确定性因素影响下目标毁伤评估问题，提出一种新的基于贝叶斯网络云模型的毁伤评估方法。分析目标特性，建立分级式评估指标体系，构建贝叶斯网络结构；将蒙特卡洛法引入参数学习之中，仿真得到各网络节点的条件概率表，利用网络推理得到目标属于各毁伤等级的概率；利用云模型将得到的目标毁伤概率转化为确定的毁伤值，从而实现由不确定性到确定性的转化。在贝叶斯网络模型中，将目标的物理毁伤程度作为功能毁伤程度的子节点之一，通过条件概率表将物理毁伤程度与功能毁伤程度联系起来，实现了一种新的物理毁伤到功能毁伤的转换方法。以雷达目标为例进行仿真实验，结果表明，该方法能够有效解决目标毁伤评估问题，且与传统贝叶斯网络模型评估结果相比，在精确度和可靠性上都有明显提高。

兵器科学与技术； 毁伤评估; 贝叶斯网络; 云模型; 雷达; 蒙特卡洛算法

0 引言

目标毁伤评估是指及时、准确地估计因己方军事力量的运用，对预定目标造成毁伤效果的评价与估量。现代战争中，作为各级指挥机关掌握战场态势、修正作战部署、明确打击重点的重要参考依据，目标毁伤效果评估已成为信息化作战条件下目标选择与打击的关键环节。

目前，国内外学者对目标毁伤效果评估进行了深入研究，提出了相关评估方法。常用的毁伤评估模型包括分层加权模型[1-2]、串并联模型[3]、网络图模型[4]、贝叶斯网络模型[5-8]、神经网络模型[9-11]等；分层加权模型通过层次分析法对评估体系的各指标赋予相应的权重系数，然后逐层进行加权求和，但该方法仅侧重于同质事物间的加权分析，使评估结果的精度不高。串并联模型用串联、并联、混联关系来简化目标间的内在逻辑关系，但由于系统目标内各子目标关系复杂，很少是简单的串并联关系，因此该方法的普适性不佳。网络图模型采用网络图的形式描述目标系统中各子目标间相互影响的关系，解决了由子目标向系统目标的过渡问题，但没有对各子目标间的关系做进一步抽象，限制了网络图模型的推广与应用。神经网络模型可以最大程度利用数据，具有较强的泛化和非线性映射能力，但在多变量、宽维度下的网络收敛速度较慢，且尚未有定量方法来确定网络参数。贝叶斯网络模型能够将先验知识与样本数据相结合、依赖关系与概率表示相结合，是数据挖掘和不确定知识表示的理想模型，在处理不确定信息的智能化系统中具有重要应用，现已成功用于医疗诊断、统计决策、专家系统等领域。但也具有以下几个缺点：1)推理结果是由概率形式表达，而概率本身就具有不确定性，使推理结果的精确性降低；2)贝叶斯网络虽然具有较为成型的参数学习理论，但参数学习通常服从某几种固定的概率分布，其合理性和准确性难以评估；3)要求网络节点均为离散型变量，无法很好地进行连续型变量的推理运算。

本文在传统贝叶斯网络模型的基础上作进一步改进。针对传统方法的局限性，引入云模型，利用其处理随机性、模糊性问题的优势，实现定性概念与定量数值之间的转化[7]，以解决贝叶斯网络推理结果不确定性问题。引入蒙特卡洛法确定贝叶斯网络的条件概率表，以解决传统服从固定概率分布使推理结果精确性降低的问题。本文提出了一种新的基于贝叶斯网络云(BN-Cloud)模型的评估方法，并将其应用于毁伤评估领域，有效解决了复杂战场环境下因不确定性、随机性因素给评估结果带来的影响，大大提高了结果的准确性。

1 贝叶斯网络模型与云模型

1.1 贝叶斯网络模型

贝叶斯网络模型可以表示为B(G,P)，其中，G表示一个节点数目有限的有向无环图，条件概率P表示有向边连接的节点间的因果关系。贝叶斯网络结构的学习本质上是关于所有网络空间的搜索过程。在确定网络结构时，必须注意防止出现有向环。

贝叶斯网络模型中的条件概率P=p(x)根据概率乘法公式[6]：

p(x1)p(x2|x1)…p(xn|x1,x2,…,xn-1),

(1)

其中，对于每个变量xi，如果有某个子集Πi∈{x1,…,xi-1}，使得xi与集{x1,…,xi-1}Πi是条件独立，即对任何的x，有

p(xi|x1,x2,…,xi-1)=p(xi|Πi).

(2)

1.2 云模型

设U是一个用精确数值表示的定量论域，C是U上的定性概念。若定量值x∈U，且x是定性概念C的一次随机实现，x对C的确定度μ(x)∈[0,1]是具有稳定倾向性的随机数。

μ:U→[0,1],∀x∈U,x→μ(x),

(3)

x在论域U上的分布称为云，每个x称为一个云滴，表示为drop(x,μ(x))。云由无数云滴构成，一个云滴即为定性概念向定量数值的一次转化实现[7]。

云利用期望Ex、熵En、超熵He3个数字特征表示，即C(Ex,En,He)，其中，期望Ex是云滴在论域空间上分布的期望，是云的重心位置，也是云滴最具代表性的数字特征。熵En为定性概念语言值的模糊度量，由语言值的模糊性和随机性共同决定，表示在论域空间可以被定性概念接受的取值范围大小。超熵He为熵的不确定性度量，即熵的熵，由En的随机性和模糊性共同决定。如图1所示为一正态云模型，具有一定的普适性。图1中，Ex=10，En=2，He=0.2，云滴数N=1 500.

图1 正态云模型Fig.1 Normal cloud model

1.3 云发生器确定条件概率分布表

云发生器是实现定性概念与定量数值之间转换的工具，可分为正向云发生器和逆向云发生器两类：正向云发生器能够实现从定性概念到定量数值的映射；逆向云发生器能够实现从定量数值到定性概念的转换。其中正向云发生器的实现算法[12]如下：

输入：定性概念D的数字特征(Ex、En、He)、N及特定值β.

输出：云滴σ对应的特定值β以及确定度μ.

算法步骤：

1) 生成一个以En为期望值，He为标准差的一个正态随机数En1=NORM(En,He2)；

2) 计算特定值β的确定度：

μ=exp (-(β-Ex)2/2(En1)2).

(4)

3) 输出一个具有确定度μ的云滴σ，即(β，μ)；

4) 重复(1)～(3)步N次，产生由N个随机云滴构成的云模型。

2 基于BN-Cloud模型的目标毁伤评估方法

本文提出了一种BN-Cloud模型，该模型充分利用了贝叶斯网络模型在不确定信息环境中较强的推理能力、云模型处理定性概念与定量数值之间转化的知识表达能力以及蒙特卡洛算法客观真实描述随机性事物特点及规律的能力。根据实际应用背景与目标特性，选取相应网络节点变量以确定贝叶斯网络拓扑结构；利用蒙特卡洛算法以随机或模拟实验构造贝叶斯网络的概率模型，得到各节点的条件概率表(CPT)；通过航空侦察、电子侦察等手段，将得到的证据信息输入贝叶斯网络模型，利用相应的推理方法，得出目标属于各毁伤等级的概率；利用云发生器将各毁伤等级转化为云模型，通过概率- 确定度转化方法，逆运算求得目标的具体毁伤值。其基本流程如图2所示。

步骤1 选定打击目标，依据目标特点与实际战场环境，选取相应网络节点变量，构建贝叶斯网络拓扑结构。

步骤2 利用蒙特卡洛算法确定贝叶斯网络模型各节点的CPT.

步骤3 打击后，利用航空图像侦察、电子情报侦察等手段确定目标毁伤的证据信息，利用推理算法对贝叶斯网络进行推理，得到该目标属于各毁伤等级的概率。

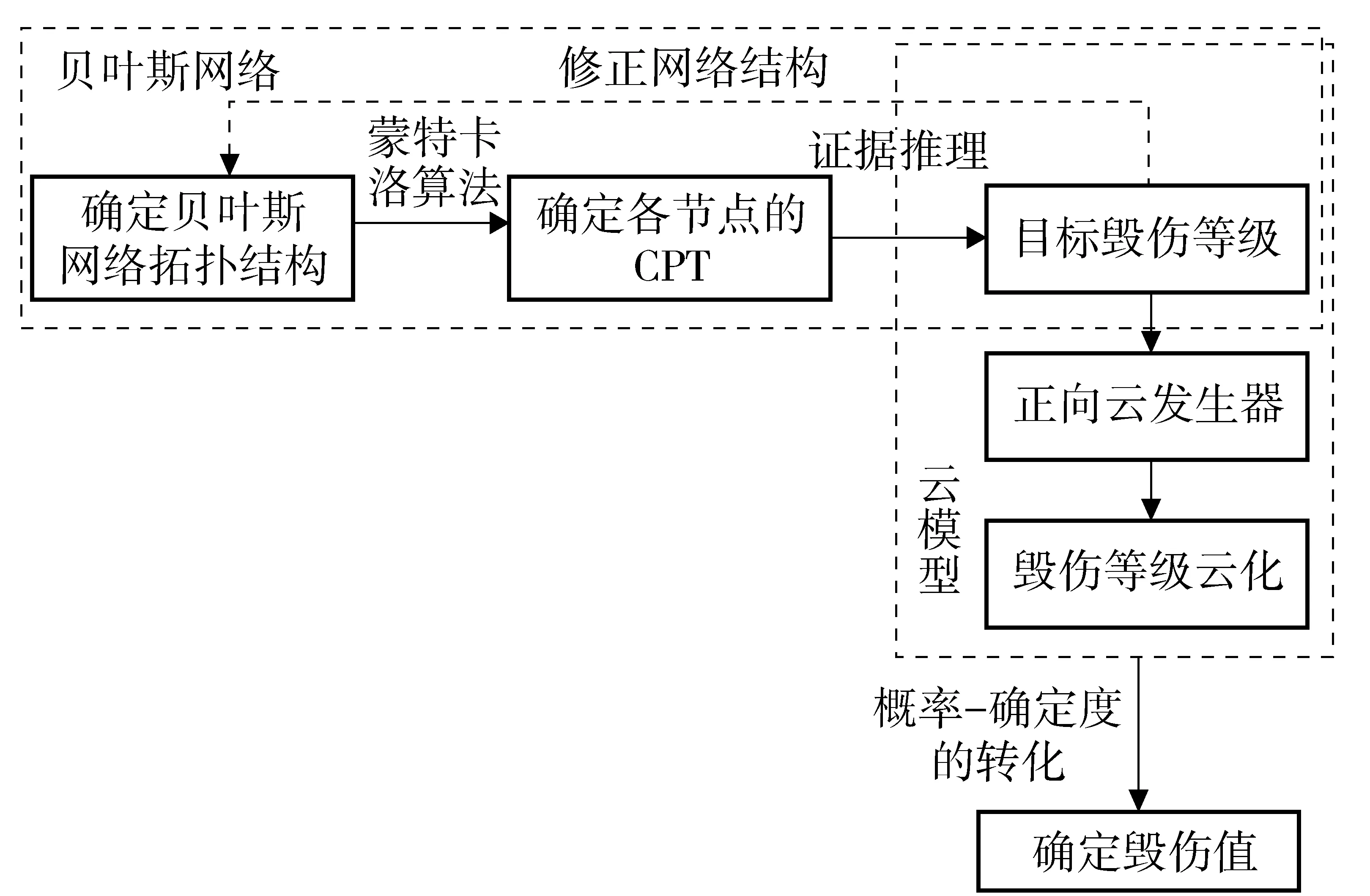
图2 基于BN-Cloud的目标毁伤评估流程Fig.2 Process of target damage assessment based on BN-Cloud model

步骤4 利用正向云发生器，将各毁伤等级转化为云模型。

步骤5 根据概率- 确定度转化方法以及云发生器原理，求出目标的实际毁伤值。

该算法的关键点有4个：蒙特卡洛算法确定CPT、毁伤等级云模型转化、概率- 确定度转化方法和实际毁伤值的求解。下面对此4个关键点进行详细描述。

2.1 确定CPT

采用蒙特卡洛算法得到CPT. 当原数据样本缺失时，蒙特卡洛算法可以通过随机实验和模拟仿真得到相对准确的推理结果。该算法的基本思想是通过已知数据推断缺失数据，从而推理得出完整的数据集，以构造出实际问题的概率模型。

蒙特卡洛算法具体的步骤如下：

步骤1 对输入数据样本初始化，弥补缺失数据，以得到数据集Dc的完整形式。

步骤2 在数据集Dc中选取一个没有被观测到的数据xil(变量xi在第l中情况)，然后计算：

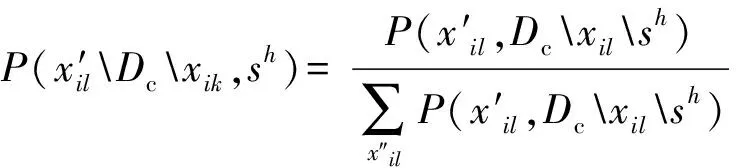
(5)

式中：x′il表示某种已存在状态；sh为第s个参数的信息；Dcxil表示去掉xil后Dc的剩余量；P(x′il,Dcxilsh)和∑P(x′il,Dcxilsh)可以通过似然公式求得。

步骤3 依据概率分布修正缺失数据，直到得到新的完整数据集D′c为止。

步骤4 返回步骤2，用新的D′c对下一轮迭代进行估计，每次迭代的参数估计P(θS|D′c,sh)均值最为最终的参数估计值，其中θs表示第s个参数的后验概率，即为要估计的参数值。

2.2 毁伤等级云模型转换

毁伤等级云模型转换就是利用云模型的3个数字特征C(Ex,En,He)表示各毁伤等级的定性语言，生成相应的云模型。

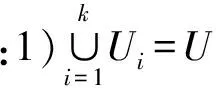
根据目标毁伤程度及要害部位受损情况，将毁伤等级划分为：摧毁、重度毁伤、中度毁伤和轻度毁伤4个等级，具体毁伤描述见表1.

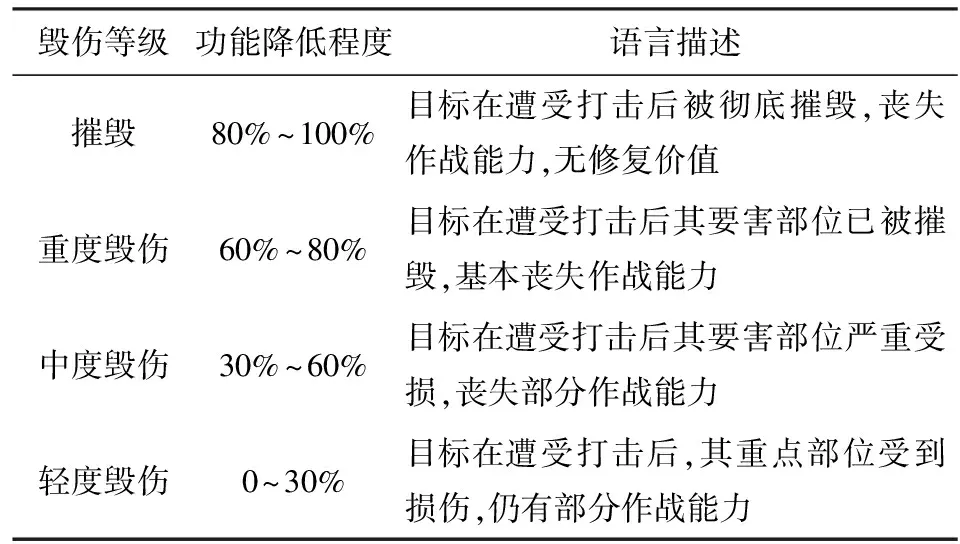
表1 目标毁伤等级评判标准

利用区间数与云模型的转换关系，将各毁伤区间转化为云模型。与正态分布的“3σ规则”类似，在云模型中一般遵循“3En规则”，即区间[Ex-3En,Ex+3En]对云模型所表达的定性概念贡献达到99.74%.

设某一毁伤区间为[ai,aj],采用指标近似法[12]确定云模型的特征参数：

(6)

式中：ω是由语言描述的随机性和不确定性决定的，一般取ω=0.05En～0.15En.

因此，由(6)式得本文毁伤论域中4个云分别表示为摧毁云CW1(0.9,0.05,0.005)，重度毁伤云CW2(0.7,0.05,0.005)，中度毁伤云CW3(0.425,0.075,0.007 5)，轻度毁伤云CW4(0.15,0.075,0.007 5)，如图3所示。

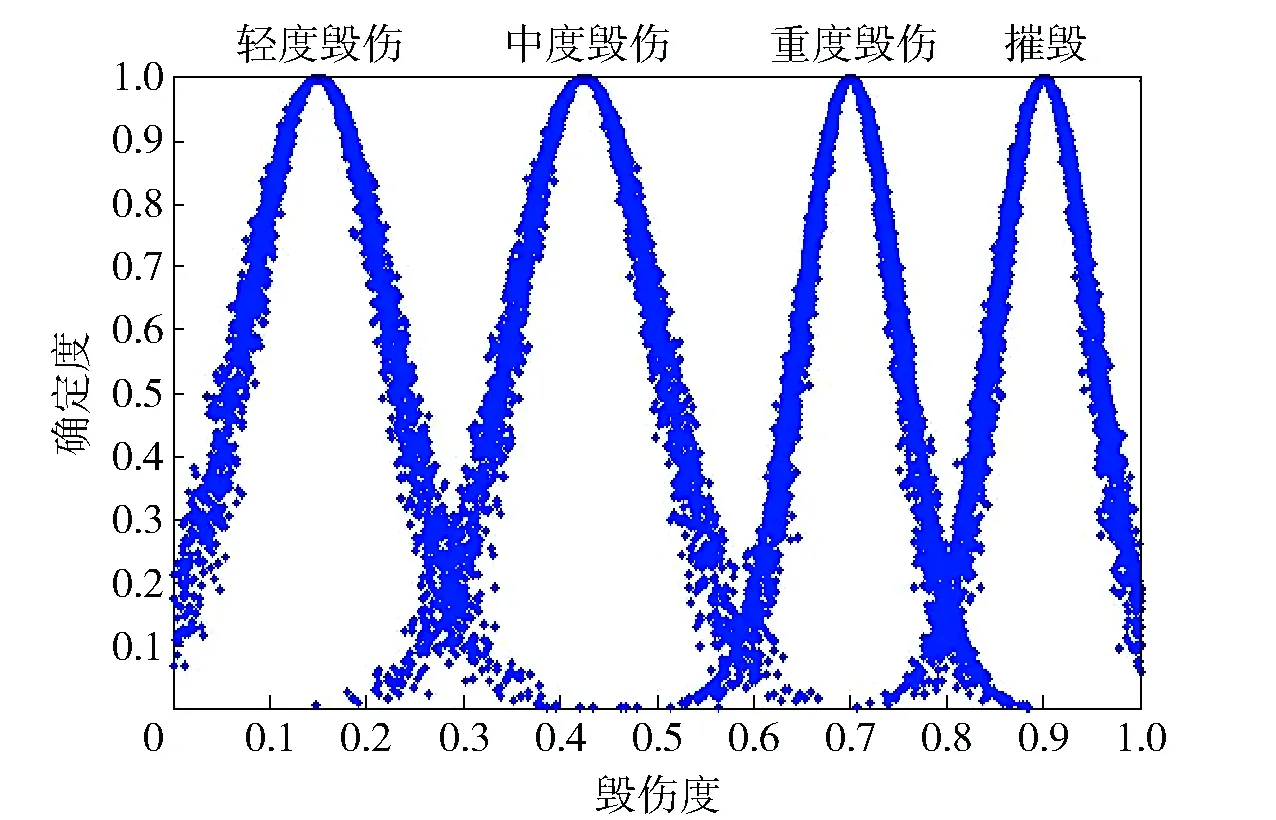
图3 毁伤等级云模型Fig.3 Cloud model of damage level

2.3 概率- 确定度转化方法

本文将云模型与毁伤等级相对应，从而使云模型的确定度与目标毁伤等级概率保持一致。云的确定度不具备概率所具有的规范性，因而，本文采用如下方法对确定度与概率进行转换：

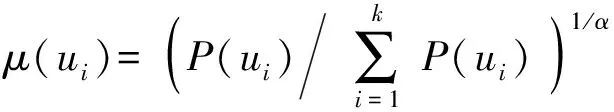
(7)

式中：μ(ui)表示确定度；P(ui)表示概率；α是检验确定度与概率一致性的常数，且α∈[0,1]，随着α的增大，二者一致性也逐渐增大。

2.4 实际毁伤值的求解方法

通过上述概率- 确定度转化公式可求得云滴的确定度，利用正向云发生器，已知定性概念D的数字特征(Ex、En、He)及确定度μ，可以逆运算求出该确定度对应的实际毁伤值为

(8)

算法实现伪代码如下：

Algorithm global strategy: Returns a specific damage value

Inputs:C(Ex、En、He), Degree of certaintyμ;

Local Variable:En1;

Outputs:β.

1: function [X,Y]=cloud(Ex,En,He)

2:En1=normrnd(En,He,1);

3: For (k=1:N)

4:E1=En1(k);

5:β=Ex+sqrt(-2(E1)2ln(μ));

6: returnβ

7: End

3 仿真实验

选取雷达目标进行毁伤评估仿真实验。将电子情报与图像情报引入雷达毁伤评估之中，综合评估雷达的物理毁伤程度，图像、电子情报相互印证，使评估结果更加准确。提出关联度的概念，给出关联度的计算方法，并与雷达修复时间、物理毁伤程度共同作为评估指标，评估雷达的功能毁伤程度，建立了一种由物理毁伤到功能毁伤的转化方法。同时，引入无人机侦察毁伤程度证据变量，反馈打击后的毁伤信息，为评估结果提供补充和验证。

3.1 定义域变量

雷达作为空天侦察的“眼睛”，具有获取空中目标的情报信息，发现、识别、追踪空中目标，并能确定其坐标位置和运动轨迹的功能。雷达天线是雷达的要害部位，其功能是接收和发射电磁波并探明方向，因此，毁伤雷达通常直接打击天线。常用球形雷达罩保护天线，直径一般在15～30 m，是电磁波的窗口。天线保护罩在航空影像上多呈灰白色，与雷达阵地背景差别较大，易于辨认[13]。

3.1.1 物理毁伤程度

物理毁伤程度是指因遭受打击，导致物理结构破坏而造成的毁伤程度。本文对雷达目标物理毁伤程度的判定，融合了图像情报和电子情报，将打击前、后目标的几何特征、结构特征以及电子信号特征进行对比分析，得出各指标的变化量，进而评估雷达的物理毁伤程度。

1)图像毁伤度。指利用航空侦察手段拍摄目标打击前和打击后的图像，通过变化检测算法确定变化区域，计算目标几何特征、结构特征等遭受打击后的变化程度，综合起来即为图像毁伤量。

2)电子信号毁伤度。指利用电子侦察手段，对表征一部雷达区别于其他雷达的固有特性参数进行提取，验证电磁信号是否由原雷达发出，当侦测信号与原信号类似，可判定雷达完好；若信号差别较大，则判定雷达已被毁伤，从而得到的雷达电子信号变化量。

3.1.2 功能毁伤程度

功能毁伤评估是在物理毁伤评估的基础上完成的，是对目标遭受打击后，剩余的作战能力或任务执行效能降低程度的评估。主要根据目标的物理毁伤程度结合目标任务、目标性质、最短修复时间以及目标之间的关联程度来评估。

1)关联度。定义：若某一目标在系统内具有的功能与其他n(n>0,n∈N*)个目标相同，则该目标与其他目标可以相互代替的程度即为关联度。它是表征目标功能的独立性以及其在系统中发挥的作用大小的一种新度量参数。由定义可知，若某一目标具有关联度，则该目标被毁伤后，可以调整其他相同功能的目标来弥补该目标功能的缺失，从而保证整个系统正常运转。

关联度C的数学表达为

C(i)=exp [-1/num(vi→vj)],i,j∈N,i≠j,

(9)

式中：num(vi→vj)表示目标vi能被vj替代的数目。关联度越大，则该目标的毁伤对系统的影响越小，因此，当目标存在的关联较少时，会对系统功能的稳定性产生较大的影响。

2)修复时间。这里的修复时间是指目标遭受打击后，恢复其所执行功能的最短时间。修复时间反映了目标的稳定性，是目标的固有属性。修复时间与功能毁伤程度息息相关，若修复时间越短，目标恢复功能越快，功能毁伤程度就越低；反之则越高。

3)无人机侦察毁伤程度参量。无人机对打击后的雷达目标进行航空侦察，实时传回目标毁伤信息，为之前的评估结果提供情报印证，是贝叶斯网络的证据变量。

4)精确度。用来评价贝叶斯网络推理得出的毁伤结果的准确性。利用无人机侦察毁伤程度证据信息，对之前推断出的毁伤结果作出高估、准确或低估的判断，可以通过此节点动态调节网络结构，以提高评估结果的准确度。

在雷达毁伤评估贝叶斯网络模型中，各个节点的状态集合如下：图像毁伤度={[0，0.3)，[0.3，0.6)，[0.6，1.0]}；电子信号毁伤度={[0，0.3)，[0.3，0.6)，[0.6，1.0]}；物理毁伤程度={轻度毁伤(LD)，中度毁伤(MD)，重度毁伤(SD)，摧毁(DD)}；修复时间={[0 h，2.5 h)，[2.5，24 h)，[24 h，+∞]}；关联度={[0，0.4)，[0.4，0.7)，[0.7，1.0]}；功能毁伤等级={LD，MD，SD，DD}；无人机侦察毁伤程度参量={LD，MD，SD，DD}；精确度={高估,准确，低估}。

3.2 定义域变量确定贝叶斯网络结构

构建贝叶斯网络时，划分不同层级结构，得到雷达毁伤效果评估的贝叶斯网络结构，如图4所示。

3.3 确定CPT

利用蒙特卡洛算法，根据(5)式得到贝叶斯网络模型各节点的CPT. 表2为物理毁伤程度节点CPT；表3为精确度节点CPT；表4为功能毁伤程度节点CPT，由于该节点CPT数据量较大且考虑篇幅限制，此处仅给出物理毁伤程度为SD情况下

的CPT.

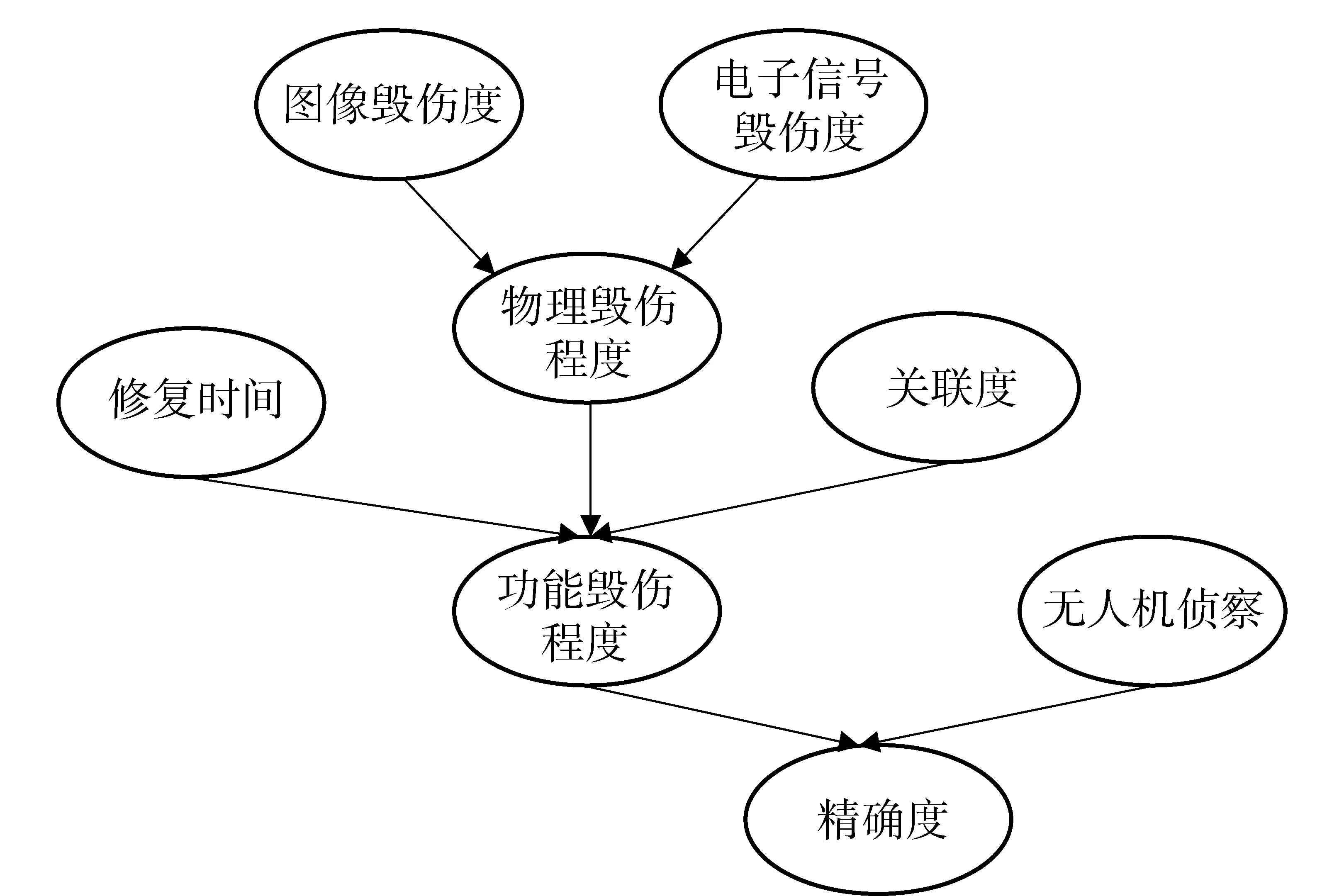
图4 雷达毁伤效果评估的贝叶斯网络结构图Fig.4 Bayesian network structure of radar damage assessment

表2 物理毁伤程度节点CPT

注：表格中每格的4个数值分别对应物理毁伤程度LD、MD、SD和DD的概率值。

表3 精确度节点CPT

注：表格中每格的3个数值分别对应精确度高估、准确和低估的概率值。

表4 功能毁伤程度节点CPT

注：表格中每格的4个数值分别对应功能毁伤程度LD、MD、SD和DD的概率值。

3.4 雷达毁伤评估仿真

3.4.1 问题假设

想定作战场景：以某次演习为例，我方出动航空兵某型战机对敌方某防空雷达阵地实施打击，以削弱敌方的对空预警能力；不考虑敌方防空反导系统对导弹造成的威胁，大气能见度较好，天空晴朗，作战时间设定为夏季某日。

作战数据如下：导弹装药量大，杀伤类型为爆破杀伤，制导精度高，无敌方电磁干扰。我方战斗机在3 000 m高空，以马赫数为0.6速度飞行，在距离目标25 km时，发射制导导弹，在距目标20 km时，导引头开机，在飞行员操控下，对目标实施打击。在对目标实施打击后，我方利用航空、航天、电子以及特种侦察第一时间对雷达阵地的毁伤效果进行评估。该雷达阵地配备3部防空雷达L1、L2、L3，天线均设有雷达罩防护，大小相近，直径约25 m，3部雷达用于搜索、监视和识别空中目标，功能相近，可互为替代。不考虑对方雷达主动关机情况，假设作战开始，分别打击3部雷达的要害部位—天线，其中导弹命中L1、L2的天线，但偏离L3(L3未被直接击中)；打击后侦测3部雷达的电子信号，仅侦测到L3的雷达信号，L1、L2静默[14]。其他相关指标参数如表5所示。

表5 雷达毁伤参数

3.4.2 仿真求解与结果分析

利用Netica软件对模型进行仿真推演。

步骤1 建立目标毁伤效果评估(BDA)推理图形，如图5所示。

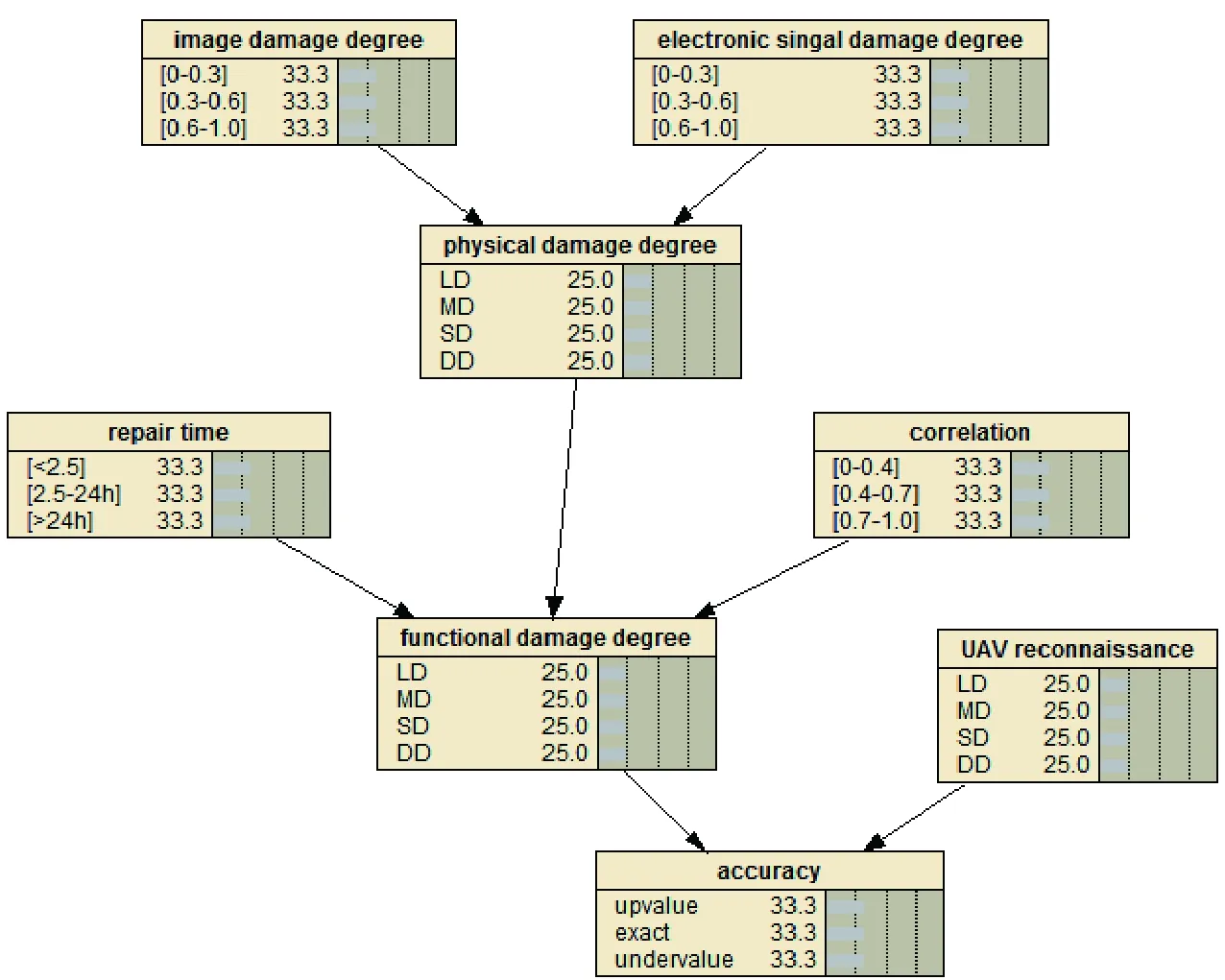
图5 雷达BDA推理图Fig.5 BDA reasoning diagram of radar

初始化，模型进入等待状态。通过仿真毁伤过程，模拟节点数据，更新BDA中的节点信息，触发网络推理，进而更新各个网络节点的概率分布，获得某一作战条件下雷达的BDA结果。

步骤2 贝叶斯网络推理。利用蒙特卡洛算法得到各节点CPT，在Netica仿真环境下，得到打击后无反馈信息(证据信息)的仿真结果如图6所示。

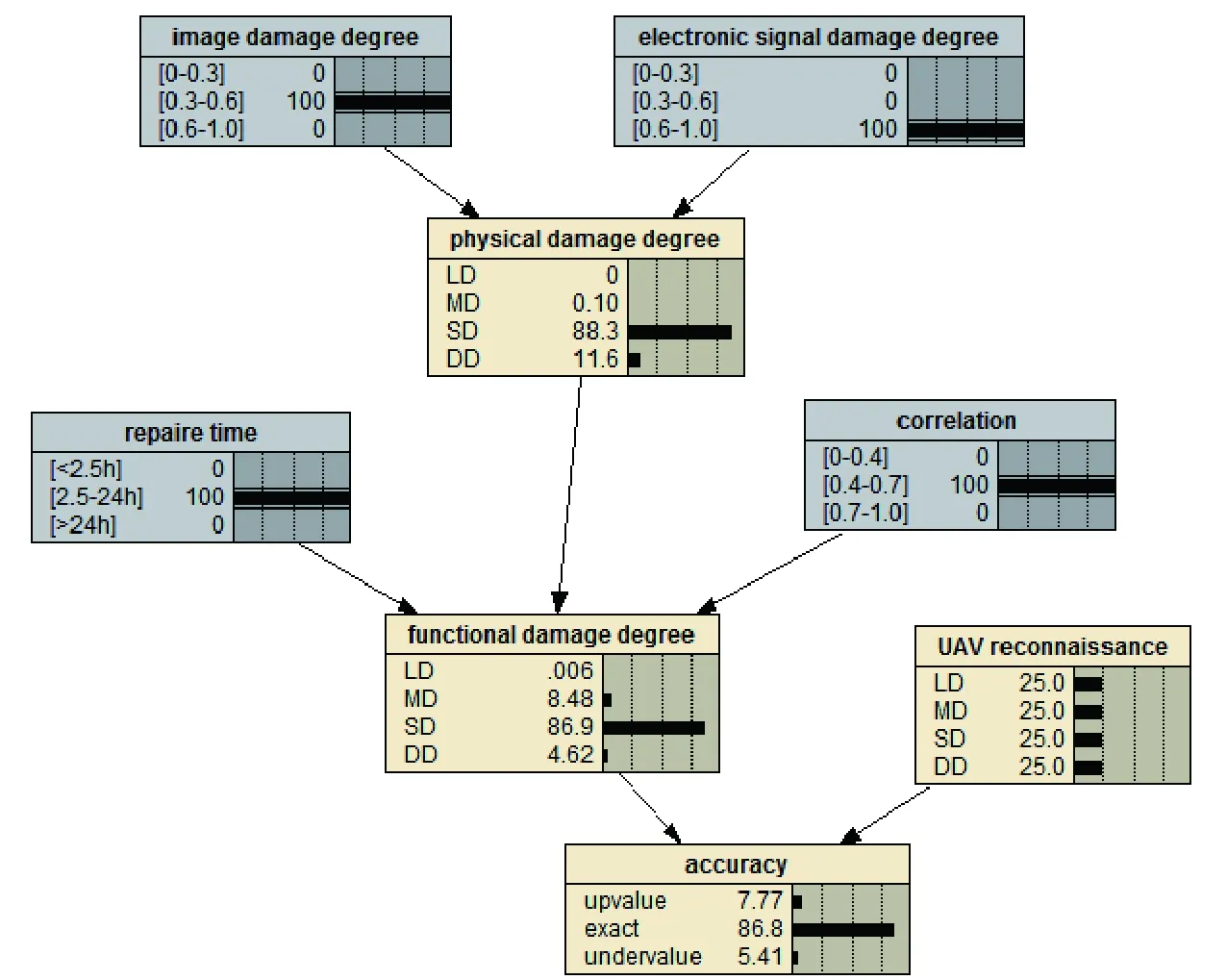
图6 无证据信息的BDA仿真图Fig.6 BDA simulation without evidence information

从图6中可以得出，雷达物理毁伤概率为：{LD，MD，SD，DD}={0，0.1%，88.3%，11.6%}；雷达功能毁伤概率为：{LD，MD，SD，DD}={0.006%，8.48%，86.9%，4.62%}；精确度概率为：{高估，准确，低估}={7.77%，86.8%，5.41%}。根据最大隶属度原则，由于雷达功能毁伤程度中的SD概率高于其他等级，可以认为在该战场状态下，雷达的毁伤等级为SD。

步骤3 贝叶斯网络证据推理。无人机侦察到雷达为SD，利用证据信息更新网络，推理得到最终的仿真结果图，如图7所示。

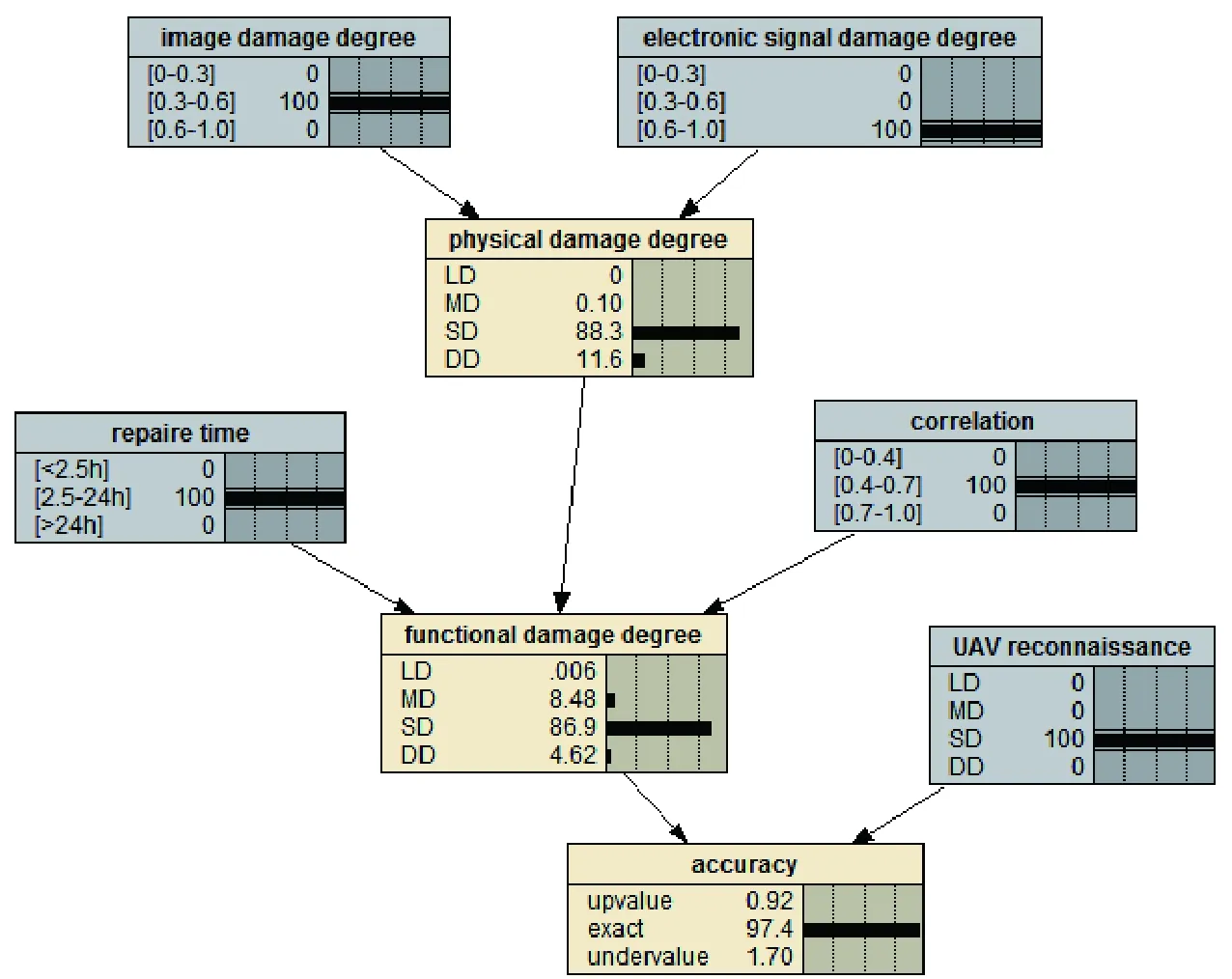
图7 加入证据信息的BDA仿真图Fig.7 BDA simulation with evidence information

由仿真结果知，输入证据信息后，精确度概率发生变化：{高估，准确，低估}={0.92%，97.4%，1.70%}；精确度属于“准确”的概率从86.9%提高到97.4%，从而加入证据之后，验证了之前的仿真结果的有效性，并使得评估精度提高。该雷达阵地为SD，达到了预期打击效果。

步骤4 概率- 确定度转化与实际毁伤值的求解。毁伤论域中4个云分别表示为DD云CW1(0.9,0.05,0.005)，SD云CW2(0.7,0.05,0.005)，MD云CW3(0.425,0.075,0.007 5)，LD云CW4(0.15,0.075,0.007 5)。当一致性检验数α=1时，由(7)式得重度毁伤的云滴确定度：

86.9%(0.006%+8.48%+86.9%+4.62%)≈

0.869 1.

(10)

将得到的确定度μ(uw2)以及重度毁伤云模型参数Exw2=0.7、Enw2=0.05、Hew2=0.005输入云发生器，输出具有相应的毁伤值β的云滴drop(β，μ)。云发生器[15]如图8所示。

利用Matlab软件进行云模型仿真，通过云发生器得到该云滴的β=0.726 5，仿真结果如图9所示；即在选定战场条件下，雷达整体毁伤程度的数值为0.726 5，相应的毁伤等级为SD.

图8 云发生器Fig.8 Cloud generator

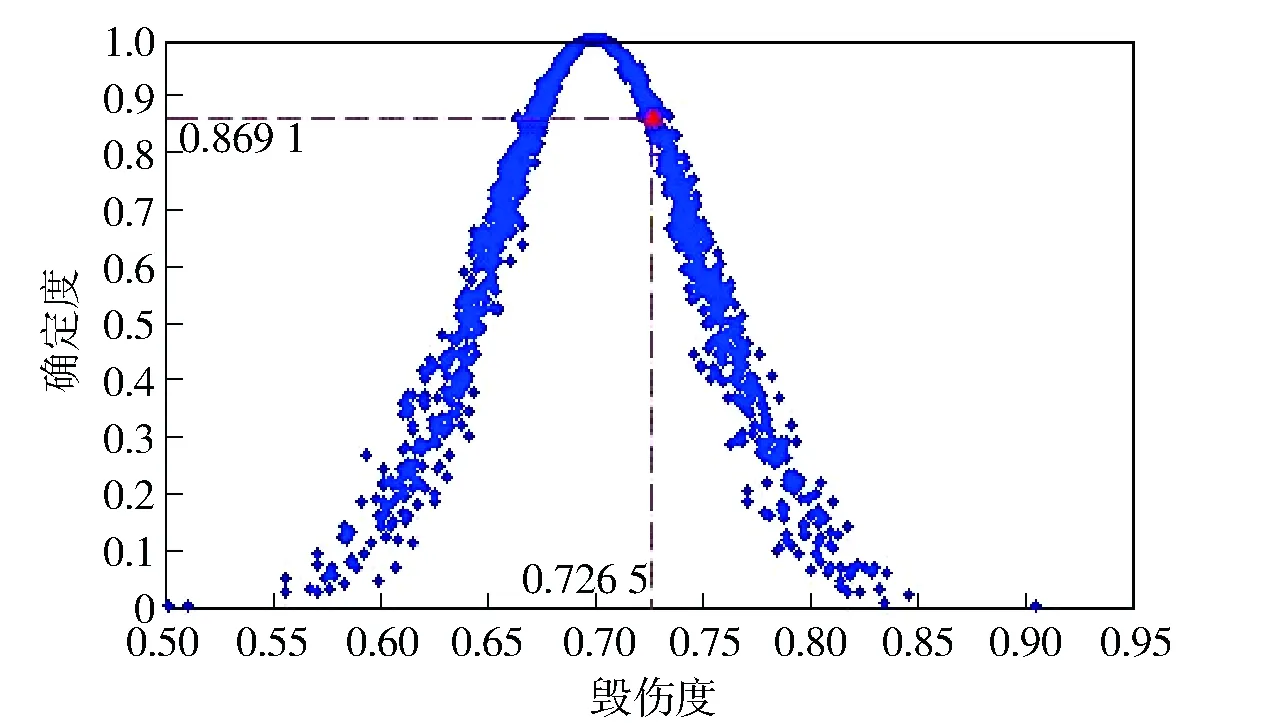
图9 雷达毁伤评估结果仿真图Fig.9 Simulated results of radar damage assessment

3.4.3 有效性分析

目前，传统贝叶斯网络[5]、神经网络[11]、模糊综合评判法[16]是毁伤评估较为普遍且稳定的算法；云重心评判法[12，15]是威胁评估领域较为常用的算法，这里稍加修改用于毁伤评估之中。将本文的实验结果与文献[5,11,16,12]方法结果进行对比分析，图10为5种方法毁伤等级概率分布对比，图11为实际毁伤值对比，具体参数如表6所示。

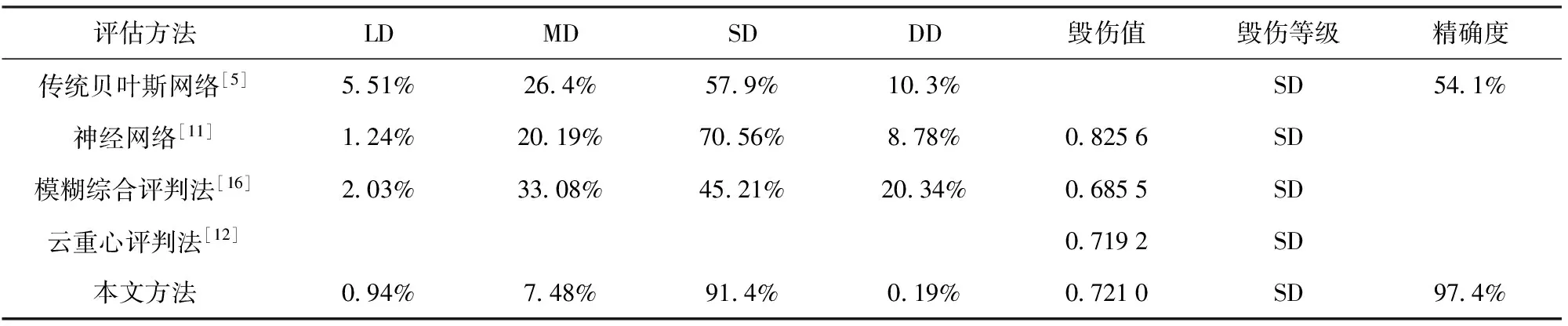
表6 本文方法与文献[5，11-12，16]方法结果对比

图10 毁伤等级概率分布对比Fig.10 Comparison of damage level probability distributions

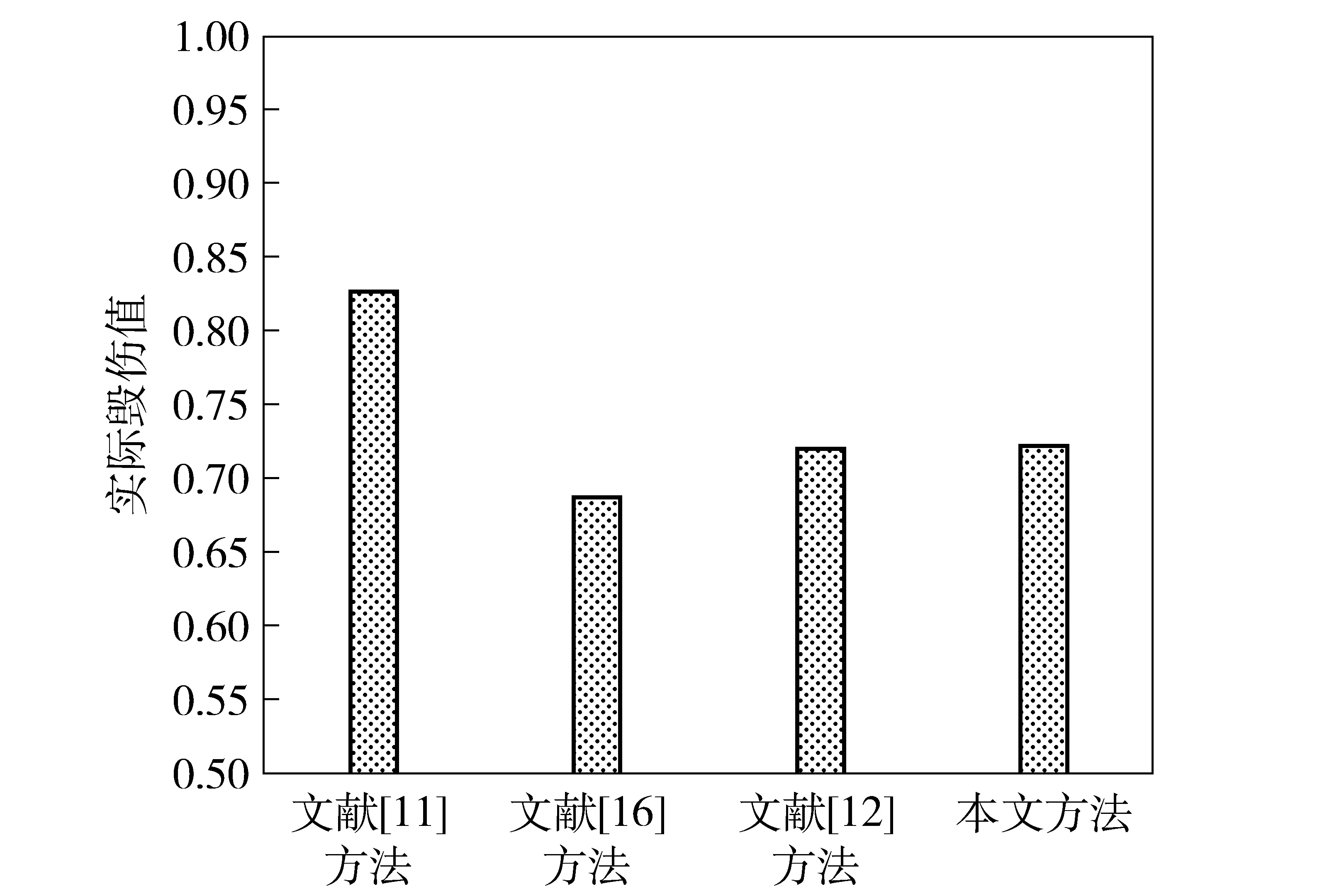
图11 实际毁伤值对比Fig.11 Comparison of actual damage values

对实验结果进行分析：

1)5种方法评估结果均为SD，验证了本文方法的正确性。

2)文献[5]方法无法得出具体的毁伤值，仅能得到各个毁伤等级的概率，而概率表征的是不确定信息，这样就会使毁伤结果的不确定性增大，可靠性降低；同时，文献[5]得到的重度毁伤概率和精确度均小于本文结果(57.9%<91.4%，54.1%<97.4%)，这是由于在评价指标选取时，仅考虑了目标自身属性和武器效能，而未考虑到目标受损后的恢复能力和与其他目标的功能关联程度，致使得到的结果准确度略低。

3)由于神经网络模型[11]仅依赖于数据，没有结合专家的知识和战场条件，若样本数据存在一定误差，则很容易得出错误结论，同时该方法也忽视了系统规则及其内部的相互影响关系，往往使得结果具有一定误差。模糊综合评判法[16]虽考虑了专家知识和战场实际，但没有充分发掘数据间的客观联系，使概率分布间距较小，各等级概率差异性不显著。

4)文献[12]方法得出的毁伤值与本文方法近似相等，说明了本文方法的有效性；而文献[12]方法无法得出目标毁伤程度属于各等级的概率，使得在推断毁伤等级时，缺少与其他毁伤等级的对比参照，给评估带来一定影响；也无法评判本次评估的精确度，这使得当评估出现较大误差时，不能根据结果误差来反馈调节算法的参数，使得该算法的准确性降低。

相比之下，本文方法结合了贝叶斯网络模型与云模型，克服了贝叶斯网络模型仅能得到毁伤等级概率和云模型毁伤判定受人为因素影响较大的问题，既考虑了专家知识和战场实际，又利用蒙特卡洛算法构造贝叶斯网格模型CPT. 既可以求解出具体毁伤值，减少了评估结果的不确定性，又综合了多种毁伤因素的影响，使得评估结果更具有可靠性。利用本文方法可以推理得到目标毁伤属于各个等级的概率，为最终判定毁伤等级提供对比参考。可以根据精确度节点值动态调节网络结构与参数，使仿真结果误差降低，从而提高算法的可靠性与准确度。

4 结论

针对传统毁伤评估方法精度不高的问题，提出了一种基于BN-Cloud模型的评估方法。

1)引入蒙特卡洛算法模拟CPT，利用贝叶斯网络模型推理毁伤等级概率，运用云模型实现定性概念与定量数据的转化，从而消除了战场条件复杂、毁伤信息难以获取、情报不确定性等给评估带来的影响，充分发挥了贝叶斯网络模型的推理能力以及云模型的知识表达能力。

2)以雷达为例进行实验仿真，提出了“关联度”的概念，可以用作目标功能毁伤评估的一种新参数。

3)为实现物理毁伤到功能毁伤的转化提供了一条新途径。

4)将本文方法的实验结果与现有算法对比，结果表明，本文算法在评估精度方面较传统方法高出43.3%(传统贝叶斯网络模型评估精确度为54.1%，本文方法评估精确度为97.4%)；可以根据精确度节点动态调整网络结构与参数，大大提高了算法的准确性与可靠性。

本文方法有效可行，为目标毁伤效果评估提供了一种新思路。

References)

[1] 姜浩，陈浩光，星学华. 基于二级模糊综合评判的机场目标毁伤效果评估[J]. 兵工自动化，2007，26(8)：1-2. JIANG Hao, CHEN Hao-guang, XING Xue-hua. Damage assessment of airport target based on two level fuzzy comprehensive evaluation[J]. Ordnance Industry Automation, 2007, 26(8): 1-2.(in Chinese)

[2] Li X H, Ci L L, Liu J H, et al. Research on battle damage assessment[C]∥7th International Symposium on Test and Measurement. Beijing, China: IEEE, 2007.

[3] 胡慧，袁震宇，谢春思，等. 基于毁伤树构建系统目标毁伤评估模型研究[J]. 舰船电子工程，2010, 30(8)：32-35. HU Hui, YUAN Zhen-yu, XIE Chun-si, et al. Research on damage assessment model of system based on damage tree[J]. Ship Electronic Engineering, 2010,30(8): 32-35. (in Chinese)

[4] 秦前付，徐征，曹存根. 基于图论的作战计划军事效果评估[J]. 计算机科学，2005，32(7)：148-151. QIN Qian-fu, XU Zheng, CAO Cun-gen. Military effect evaluation of operational plan based on graph theory[J]. Computer Science, 2005, 32(7): 148-151. (in Chinese)

[5] 李望西，黄长强，吴文超，等. 空地精确制导武器对地攻击目标毁伤评估[J]. 系统工程理论与实践，2012,32(1)：211-218. LI Wang-xi, HUANG Chang-qiang, WU Wen-chao, et al. Battle damage assessment of air-to-ground precision guided weapon air-to-ground attack[J]. System Engineering- Theory & Practice. 2012,32(1): 211-218. (in Chinese)

[6] 金焱，胡云安，张瑾，等. 基于贝叶斯网络的某机载雷达电磁损伤评估[J]. 北京理工大学学报，2012，23(9)：960-975. JIN Yan, HU Yun-an, ZHANG Jin, et al. Electomagnetic damage assessment of airborne radar based on bayesian networks[J]. Transactions of Beijing Institute of Technology, 2012, 23(9): 960-975. (in Chinese)

[7] Soles A M, Walsh M R, Scott E B. Damage detection and remediation system and methods thereof，US, 0188078 A1[P]. 2012-07-26.

[8] 眭海刚，华凤，范一大，等. 利用GIS与贝叶斯网络进行高分辨率SAR影像道路损毁信息提取[J]. 武汉大学学报:信息科学版，2016，41(5)：578-583. SUI Hai-gang, HUA feng, FAN Yi-da, et al. Road damage extraction from high-resolution SAR image based on GIS data and Bayes network[J]. Geomatics and Information Science of Wuhan University, 2016, 41(5): 578-583. (in Chinese)

[9] 吴正龙，赵忠实. 基于自适应模糊神经网络系统的射击毁伤评估模型研究[J]. 兵工学报，2012，33(11)：1352-1357. WU Zheng-long, ZHAO Zhong-shi. Research on fire damage assessment model based on adaptive fuzzy neural network system[J]. Acta Armamentarii, 2012, 33(11): 1352-1357. (in Chinese)

[10] 倪敏，彭宜青，罗喻. 神经网络和DEA方法的炮兵火力毁伤先验评估模型[J]. 火力与指挥控制，2012，37(2)：127-131. NI Min, PENG Yi-qing, LUO Yu. The model of prior evaluation of artillery firepower bombardment based on neural network and DEA[J]. Fire Control & Command Control. 2012, 37(2): 127-131. (in Chinese)

[11] Meruane V, Mahu J. Real-time structural damage assessment using artificial neural networks and antiresonant frequencies[J]. Shock and Vibration, 2014，62(7): 118-124.

[12] 张成，石全，刘铁林. 云重心评判法在目标毁伤效果评估中的应用[J]. 计算机仿真，2012，29(9)：28-31,45. ZHANG Cheng, SHI Quan, LIU Tie-lin. Study on application of cloud barycenter evaluation method to battle damage assessment[J]. Computer Simulation, 2012, 29(9): 28-31,45. (in Chinese)

[13] Lowe D G. Method and apparatus for identifying scale invariant features in an image and use of same for locating an object in an image， US, 6711293[P]. 2014-04-08.

[14] TNO.Lethality_and_Protection[DB/OL].[2013-09-19].http:∥www.tno.nl/downloads/9_IB_Lethality_and_Protec-Tion.pdf.

[15] 刘勇，徐廷学，孙海燕. 基于改进云重心方法的装备维修性定性评价 [J]. 火力与指挥控制，2014，39(3)：64-68. LIU Yong, XU Ting-xue, SUN Hai-yan. Equipment maintainability qualitative evaluation based on improved cloud barycenter method[J]. Fire Control & Command Control, 2014,39(3): 64-68. (in Chinese)

[16] 王晋平，段卓平，刘彦. 坑道目标毁伤效果的模糊综合评估研究[J]. 北京理工大学学报，2015，35(8)：771-776. WANG Jin-ping, DUAN Zhuo-ping, LIU Yan. Damage assessment for tunnel target based on fuzzy synthesize assessment[J]. Transactions of Beijing Institute of Technology, 2015, 35(8): 771-776. (in Chinese)

Battle Damage Assessment Method Based on BN-Cloud Model

QU Wan-jia1, XU Zhong-lin1, ZHANG Bo-lin2, LIU Ying1

(1.Aviation University of Air Force, Changchun 130022, Jilin, China; 2.Unit 94810 of PLA, Nanjing 211500, Jiangsu, China)

A new damage assessment method based on BN-Cloud model is put forward for the impact of complex and uncertain factors in modern battlefield environment. The characteristics of targets are analyzed, and a hierarchical evaluation index system is established, which is used to build a Bayesian network (BN) structure. Monte Carlo method is introduced into parameter learning, a condition probability table (CPT) of each network node is obtained through simulation, and the probability of each damage level is obtained by using the network inference. Finally, cloud model is used to transform target damage probability into real damage value so as to realize the transformation from uncertainty to certainty. The target physical damage degree is used as one of sub-nodes of functional damage degree in BN, in which CPT is used as a link. As a result, a new method to transform physical damage into function damage is realized. A radar target is taken as an example for simulation. The simulated result shows that the proposed method can be effectively used for target damage assessment, and achieves a significant improvement in accuracy and reliability compared with the existing algorithms.

ordnance science and technology; damage assessment; Bayesian network; cloud model; radar; Monte Carlo algorithm

2016-06-02

武器装备军内科研项目(KJ2013122)

曲婉嘉(1992—)，女，硕士研究生。E-mail：1259737654@qq.com 徐忠林(1969—)，男，副教授，硕士生导师。E-mail: xu_zhanglin@sina.com

E919

A

1000-1093(2016)11-2075-10

10.3969/j.issn.1000-1093.2016.11.016