长江下游水体藻类对含沙量烘干法测定准确度影响分析
2016-12-15韦立新郭德俊
王 悦 韦立新 郭德俊
(长江委水文局长江下游水环境监测中心,江苏 南京 210011)
长江下游水体藻类对含沙量烘干法测定准确度影响分析
王 悦 韦立新 郭德俊
(长江委水文局长江下游水环境监测中心,江苏 南京 210011)
以长江下游水体优势种藻类为研究对象,采用烘干法测量含沙量,通过计算全年极限系统误差和月际实际系统误差,分析水体藻类密度和组成对含沙量烘干法测定结果准确度的影响。结果表明,在长江下游地区,极限系统误差值为0.43%,各月实际系统误差变化范围为0.002%~0.155%,平均值为0.036%,均远小于系统误差允许值,说明下游水体藻类对含沙量烘干法测定结果的准确度几乎无影响。
水体;藻密度;硅藻门;烘干法;含沙量;长江下游
水体泥沙含量的测定,在水利水电工程建设、水文测报及水土流失治理等领域具有重要的科研与经济价值[1]。考虑到水体中生活的藻类可能会影响含沙量监测的准确度,本文就长江下游近岸水体藻类对含沙量烘干法测定准确度的影响开展基础性研究。
1 研究区域及方法
1.1 研究区域
本研究选取每月藻类监测点与含沙量采样点最接近区域进行比较分析,其中藻类采样点选取南京大胜关自动监测站右岸表层水体Ⅲ上,南京站含沙量监测选取南京水文试验站流速仪测流断面右岸(垂线10),两采样点相距50 m,采样位置如图1所示。
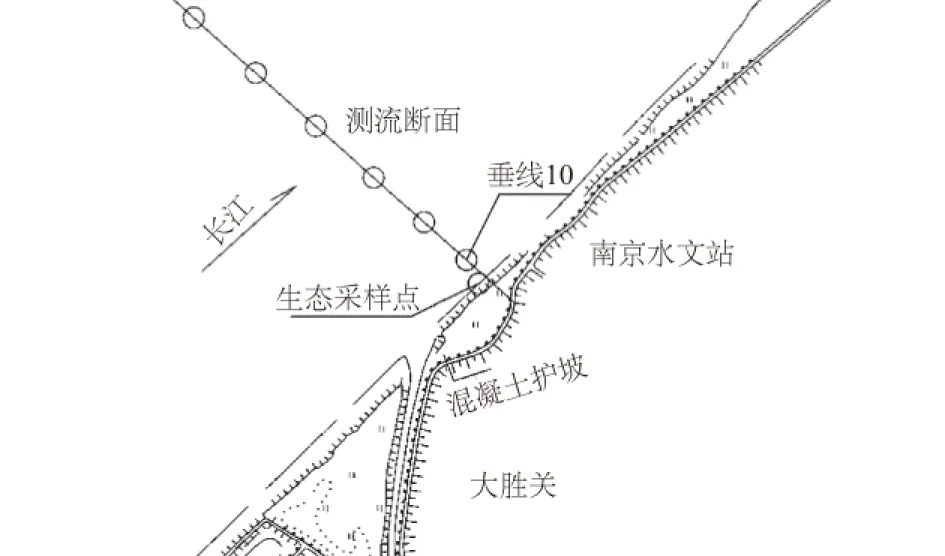
图1 采样位置示意
1.2 研究方法
利用2015年生态监测藻类群落组成、藻密度成果数据及南京站提供的单测次含沙量数据进行分析。根据《河流悬移质泥沙测验规范》(GB/T50159—2015)以及系统误差(同体积藻类重量/水样含沙量)不大于1%时无影响[2],因此考虑分析极限值情况。
以含沙量采样点(垂线10)2015年含沙量最小测次为含沙量极小值,作为影响分析下限;各月藻类监测中单位体积重量最大的测次为藻类重量极大值,作为影响分析上限。通过比较含沙量月际变化最小值与藻类重量月际变化最大值获得极限系统误差。同时统计各月对应藻干重与含沙量系统误差变化,获得月际实际系统误差变化。通过分析比较极限系统误差、实际系统误差两者与系统误差允许值(1%)的差别来作出判断。若两者均不超过1%,则可说明藻类对含沙量测定准确度无影响;若任一系统误差大于1%,则需进一步设计实时监测补充试验。
1.2.1 含沙量测定
含沙量数据依据《河流悬移质泥沙测验规范》(GB/T50159—2015),采用烘干称重法获得,即经过量积、沉淀、过滤、烘干、称重等步骤,得出一定体积水体中的干沙重量[2]。单位体积内所含干沙的质量,称为含沙量,用Cs表示,单位为kg/m3。
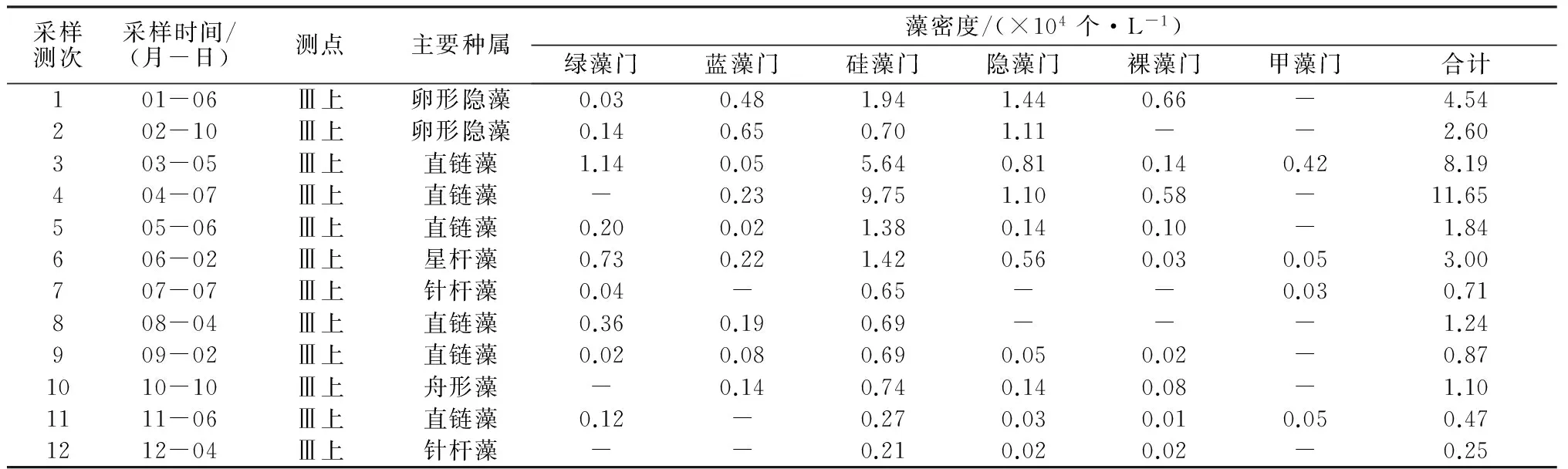
表1 2015年南京大胜关自动监测站藻类生态监测成果
1.2.2 藻类重量测定
藻类数据获得依据《水库渔业资源调查规范》(SL167—2014),镜检统计藻类种类组成及对应藻密度[3]。单位体积藻类湿重采用体积换算为生物量(湿重)方法,与水体相对密度近似为1;体积的测定根据浮游植物的体型,按最近似的几何形状测量必要长度、高度、直径等,换算出实际体积,并计算出每种藻类的平均湿重[4]。湿重还可以通过换算方式转变为干重,一般藻类含水率为90%以上[5],本研究以90%计算,则计算公式如下:
(1)
(2)
式中,M为单位体积藻类生物量,g/L;K为单位体积藻类总干重,g/L;Ni为单位体积水样第i种藻类藻密度,个/L;Vi为单位体积水样第i种藻类平均体积,μm3/个;ρH2O为水的密度,kg/m3;WH2O为含水率,%。
2 测量及统计结果
2.1 含沙量统计
本次含沙量数据来自南京站2015年实测数据,统计其右岸水面含沙量数据(垂线10,相对水深0.2,水深范围2.5~4.0m)。由图2可知,含沙量最小值位于2月26日附近,采用实测值 0.014 kg/m3作为含沙量极小值。

图2 2015年南京大胜关断面实测含沙量过程线
2.2 藻类湿重计算
2015年藻类生态监测成果如表1所示。分析全年数据可知,全年藻密度最大月份为4月,合计11.65×104个/L,优势种为硅藻门直链藻属,组成比例为:蓝藻门1.97%,硅藻门83.69%,隐藻门1.10%,裸藻门4.98%。由于绝大多数类群为硅藻门,并且根据现成资料主要浮游植物细胞的平均湿重,直链藻较其他硅藻门藻类平均湿重大,细化至各种藻类分析对极值法影响较小,故将样本拟定为100%直链藻属,即直链藻属藻密度=11.65×104个/L。
根据直链藻体积公式V=πr2h[4],其中,r为浮游植物几何体型的半径,μm;h为高度,μm。经测量和计算,直链藻属平均体积为 5.296×103μm3/个。
3 误差分析
3.1 极限系统误差值
由上述统计分析可知,直链藻属藻密度为11.65×104个/L,平均体积为5.296×103μm3/个,由公式(2)可得单位体积藻类总干重,即K=6.170×10-5kg/ m3。
由上文可知,最大K值为 6.170×10-5kg/m3,含沙量最小值为 0.014 kg/m3,则极限系统误差(同体积藻类重量最大值/水样含沙量最小值)为0.43% 。
3.2 实际系统误差值
根据现有资料统计的主要浮游植物细胞的平均湿重及各门藻类按对应属平均湿重(无对应资料时按相近属最大值计算)[4],利用单位体积藻类总干重K,换算各月藻类干重[4]。统计各月含沙量算术平均值,计算与各月藻类干重系统误差值,得出各月藻类干重过程线和各月系统误差过程线(见图3,4)。

图3 2015年各月藻类干重过程线

图4 2015年各月系统误差过程线
由图3和图4可知,长江下游月际藻类干重变化与藻密度变化基本一致,大部分月份均同步变化。其中藻密度、干重、系统误差峰值均集中于3、4月份, 其余月份仅为峰值的1.3%~32%。
综上,下游近岸水体各月藻类干重变化与各月系统误差变化趋势一致,极限系统误差值为0.43%,各月实际系统误差变化范围为 0.002%~ 0.155%,平均值为 0.036%,中位数为 0.017%,均远小于1%,故判定藻类对含沙量测定准确度无影响。但考虑到长江流域藻类分布不均匀这一现状,分析由古代硅藻的遗骸所组成的硅藻土,其化学成分以SiO2为主,具有众多的壳体孔洞,松散密度为0.47 g/cm3[6]。针对其上述特征,可采用过滤浓缩水样,坩埚加热至灰白后转入离心管,快速离心去除上层液体,并通过镜检判断去除率,从而获得基本去除硅藻门藻类的测定水样,可为今后相关测定方法的研究工作提供参考。
4 结 论
本文采用全年极限系统误差值和月际实际系统误差值对比分析长江下游水体藻类对含沙量烘干法测定准确度的影响,结果表明,由于下游藻类藻密度过低,对含沙量测定结果准确度几乎无影响。若考虑推广至长江流域,由于藻类分布不均匀,特别是上游及库区藻密度较大,则极可能对含沙量烘干法造成影响。
[1] 水利部水文局. 江河泥沙测量文集[M].郑州:黄河水利出版社,2000.
[2] GB/T50159—2015河流悬移质泥沙测验规范[S].
[3] SL167—2014水库渔业资源调查规范[S].
[4] 章宗涉,黄翔飞. 淡水浮游生物研究方法[M].北京:科学出版社,1995.
[5] 国家环境保护总局编. 水和废水监测分析方法[M]. 第4版. 北京:中国环境科学出版社,2002.
[6] Gendron-Badou A, Coradin T, Maquet J, et al. Spectroscopic characterization of biogenic silica [J]. Journal of Non-Crystalline Solids, 2003, 316:331-337.
(编辑:陈紫薇)
2016-09-15
王悦,女,长江委水文局长江下游水环境监测中心,工程师.
1006-0081(2016)11-0065-03
S968.41
A
