基于实时电价的多目标电动汽车控制策略

涂轶昀

(上海电力学院 电气工程学院, 上海 200090)



基于实时电价的多目标电动汽车控制策略

涂轶昀

(上海电力学院 电气工程学院, 上海 200090)

在实时电价的电力市场机制下,综合考虑了电网侧和电动汽车车主双方利益,建立了电动汽车群接入电网后的控制模型.该模型以电动汽车群接入电网后负荷曲线峰谷差最小及电动汽车车主收益最大为优化目标,并以电池充放电功率和可用容量为约束条件,采用粒子群算法进行了优化求解,得出了电动汽车群与电网的交互功率曲线.最后,通过仿真实例验证了所建构模型的正确性和有效性.

电动汽车; 实时电价; 多目标控制策略

随着各国对环境问题的日益重视,PM2.5污染物的重要组成部分——汽车尾气,成为治理的重点.电动汽车采用电池作为驱动汽车行驶的能量来源,尾气排放几乎为零,成为我国汽车工业的重点发展对象,并得到了长足的发展.

削峰填谷是电动汽车接入电网的主要功能,负荷高峰时期电动汽车作为电源向电网送电,负荷低谷时期电动汽车作为负荷消耗电能,可以起到拉平负荷曲线、减小负荷峰谷差的作用.对于电网公司而言,这是很有利的.同时,换电站的兴起,也方便电网公司对电动汽车蓄电池的调度和控制,实现调峰的难度大大降低.

电动汽车参与电网调峰后,不仅能平抑负荷功率波动,而且在实时电价的基础上,能利用不同时段的电价差获取收益.

然而,如果没有合理的控制策略,其与电网的配合也可能造成“峰上加峰”的恶劣影响,从而阻碍电动汽车的发展.在电力系统中引入市场机制,不仅可以引导用户合理用电,而且可以引导电动汽车车主的充放电行为,从而将电网的效益与电动汽车车主的收益结合,达到双赢的局面[1-8].

在电动汽车充放电调度方面,国内外学者已经做了大量研究.例如,文献[3]研究了电动汽车接入电网的作用、商业模式、实现步骤等;文献[4]提出了在电动汽车渗透率较高时,由短期负荷趋势对各时段可充电功率进行优化的电动汽车智能充电方法;文献[5]构建了充电时间对峰谷电价时段的响应模型,以峰谷差率最小为目标函数,通过遗传算法对峰谷电价时段优化问题进行了求解;文献[6]建立了电动汽车参与负荷平抑的数学模型,采用改进粒子群算法求解出电动汽车参与负荷平抑的充放电控制策略;文献[7]采用二次规划和动态规划优化了电动汽车充电策略.

然而,上述研究都没有综合考虑电网公司和电动汽车车主双方的利益,本文采用实时电价的电力市场机制,建立单目标和多目标电动汽车优化调度的数学模型,通过粒子群算法求解,得到相应的电动汽车群充放电计划,最后,通过仿真算例验证调度策略的有效性,比较不同目标函数的优化效果.

1 实时电价的电力市场机制

电力市场机制是电能生产者和使用者通过协商、竞价等方式就电能及其相关产品进行交易,通过市场竞争确定价格和数量的机制.电价作为电力市场中的经济杠杆,可以实现电力市场中资源优化配置的目的.

目前,我国实行的是峰谷平电价,今后还要推行居民用电阶梯电价制度.“阶梯电价”是指把户均用电量设置为若干个阶梯,各阶梯用电量和电价均采用递增模式.此举有利于鼓励居民节约用电、减少能源浪费,还可以提高能源效率.

然而,成熟的电力市场实施实时电价政策,即用电高峰时段釆用高电价,用电低谷时段采用低电价,可引导部分负荷转移至电网谷负荷的低电价时段.当我国电力市场发展成熟以后,实时电价的推行是今后电力改革的重要方向.

实行实时电价,用户会自发对电价进行响应,调整用电时间,以谋求最大的经济效益,从被动地受供电部门控制到主动参与负荷的调整.

电动汽车作为未来电力负荷的重要组成部分,同时作为新型储能放电电源,通常在工作时段和晚上都处于停驶状态.一般来说,电动汽车电池的容量远远大于正常上下班行驶的电能消耗容量,因此电动汽车不仅可以在负荷低谷时进行充电实现填谷功能,还可以在高峰时段接入电网实现削峰作用.在智能电网发展成熟阶段,智能充放电装置可根据实时电价信号为用户设置最经济的充放电方案,引导电动汽车响应实时电价,实现智能充放电[9].

2 单目标电动汽车优化控制模型

在电动汽车接入电网的初级阶段,电动汽车数量有限,可实现的调节容量较小,对地区负荷曲线影响不大,但是可以改善商业楼宇(或居民小区)的负荷曲线.已知负荷曲线后,如何合理安排辖区内电动汽车的充放电时间和充放电功率是需要解决的关键问题.同时,也可以从电动汽车车主的角度出发,以车主从电价差中获取的收益最大为目标函数.

2.1 以电网负荷峰谷差最小为目标函数

电动汽车接入电网后,可以利用其电池储存的能量与电网进行功率交换,高峰时期提供电能,低谷时期消耗电能,从而实现减小负荷峰谷差的目的.

电动汽车控制中心以响应区域负荷的方式参与调峰,同样将1d分为24个时段,以负荷曲线的均方差最小为目标函数,其方程为:

(1)

式中:Pj——调整前的原始负荷;Pij——第i辆车在j时段与电网的交换功率;

i——电动汽车序号;

j——时段序号.

2.2 以电动汽车车主收益最大为目标函数

本文将1 d分为24个时段,在施行实时电价的基础上,每一个时段市场中的电价都是有差异的.根据实时变化的电价,用放电行为带来的收益减去充电行为消耗的成本,即电动汽车并网充放电行为给用户带来经济方面的差价收益.

其目标函数为:

(2)

(3)

(4)

式中:n——电动汽车辆数;t——充/放电时长,这里取1 h;p(j)——第j时段的市场电价,元/kWh;Cij——第i辆车在j时段的充电成本;Rij——第i辆车在j时段的放电收益;Pij——第i辆车在j时段与电网的交换功率(设充电功率为负值,放电功率为正值);

Effc,Effd——车载电池的充电、放电效率,均取0.9.

2.3 约束条件

(1) 充放电功率约束.功率约束主要体现在电池最大充放电功率上,充放电功率约束为:

(5)

式中:Pijmin,Pijmax——电动汽车最大充、放电功率;

(2) 电池可用容量约束.电动汽车的电池容量是一定的,其电量状态可用SOC(State-of-Capacity)表示,电池处于充满状态时SSOCmax=1,考虑到电池深度放电对电池的影响不可逆,通常设置SSOCmin=0.2.即:

(6)

若用电池容量来表示,则为:

(7)

式中:SSOCij——第i辆车在j时段的电量状态;QiN——第i辆车的额定容量值;Qi,j-1——第i辆车在(j-1)时段的容量值; ΔQij——第i辆车在j时段的充(放)电容量.

(3) 充电功率与充电电量的关系,即[10-12]:

(8)

(9)

式中:Qi,j——第i辆车在j时段的容量值;Qi,j+1——第i辆车在(j+1)时段的容量值.

3 多目标电动汽车优化控制模型

将电动汽车的调峰功能与电动汽车车主利用实时电价差的收益结合起来,既考虑负荷曲线的调峰作用,又考虑电动汽车车主的收益,即可实现多目标的电动汽车控制策略.

(1) 目标函数 本文将负荷曲线的均方差最小和电动汽车车主的收益最大按照不同的权重系数结合起来,其目标函数为:

(10)

式中:F1max,F2max——F1和F2的最大值,用于两个目标函数的归一化;

λ1,λ2——目标函数的权重系数,λ1+λ2=1,0≤λ1,且λ2≤1;

(2) 约束条件 多目标电动汽车优化控制模型的约束条件与单目标电动汽车优化控制模型相同.

4 仿真算例及分析

4.1 基础数据

以某电动汽车群响应给定的实时电价曲线为研究对象,假设电动汽车的电池参数统一,以BYDE6为参考,表1给出了电池参数数据.

表1 电动汽车群的电池参数

假设在一个时段内充、放电功率恒定不变,其最大充电功率为7 MW,最大放电功率为15 MW,电动汽车群的初始电池容量状态为0.8.

以某变电站供电的商业区价格曲线来反映电价波动,如图1所示.

表2给出此变电站日负荷功率值,即加入电动汽车前的原始负荷功率,负荷值以小时为间隔.

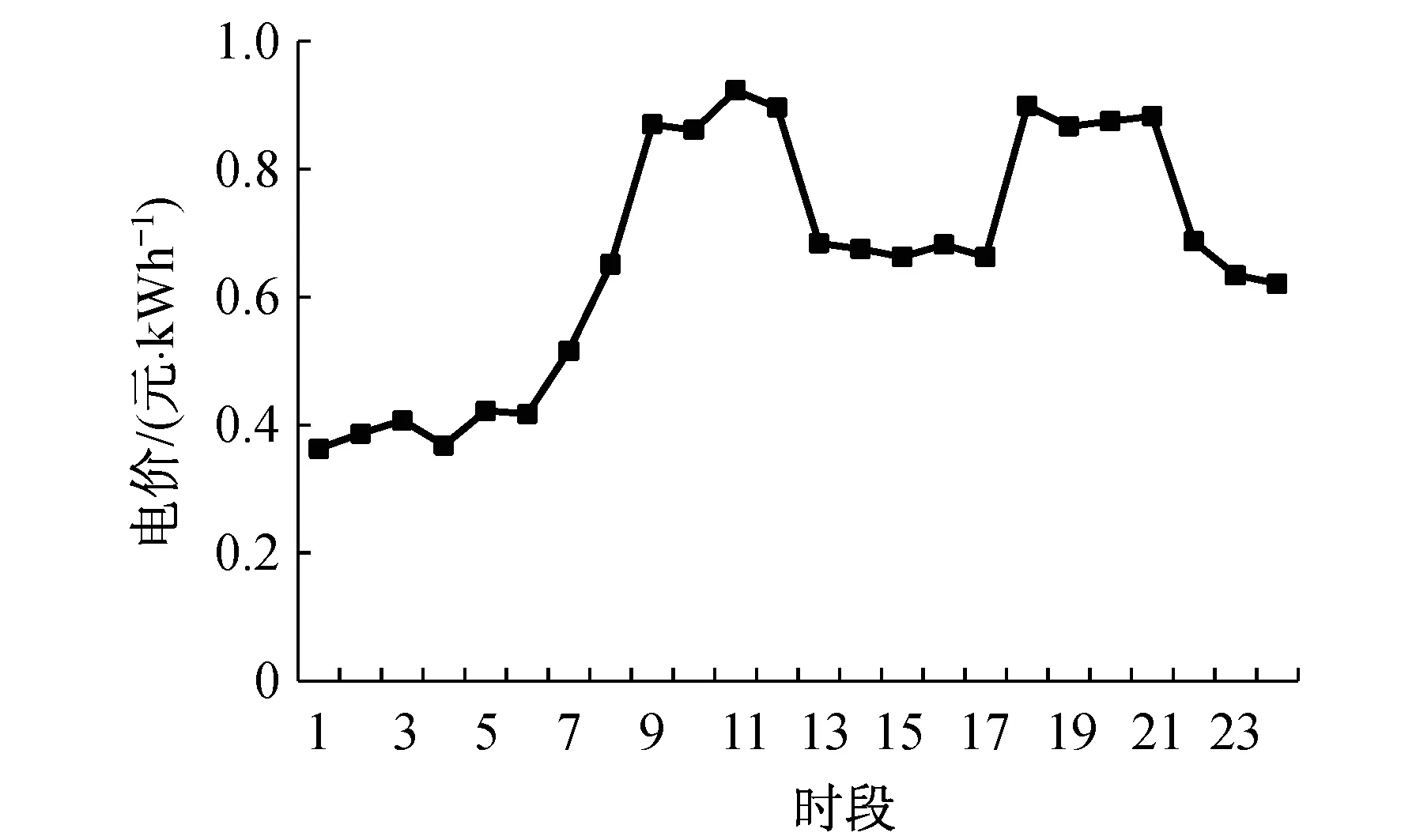
图1 某商业区24 h实时电价曲线

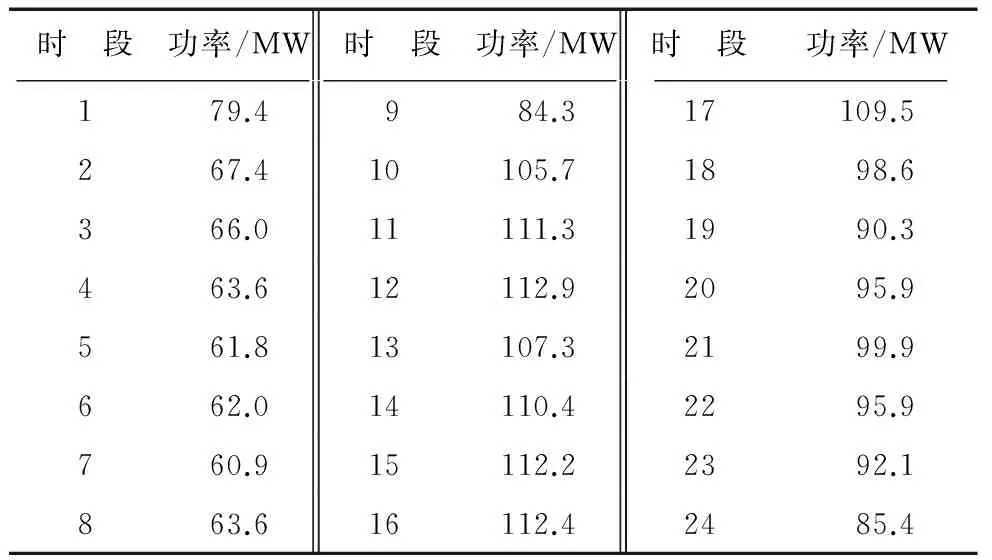
时 段功率/MW时 段功率/MW时 段功率/MW179.4984.317109.5267.410105.71898.6366.011111.31990.3463.612112.92095.9561.813107.32199.9662.014110.42295.9760.915112.22392.1863.616112.42485.4

4.2 运行结果及分析

4.2.1 以电网负荷峰谷差最小为目标的优化结果

在目标函数为电网负荷峰谷差最小的情况下,通过粒子群算法进行优化计算.惯性权重因子ω取值范围为0.4～0.9,最大迭代次数为2 000;粒子群规模为30;粒子速度阈值按经验取最大值为4,最小值为-4[13].

优化计算后电动汽车群在各个时段与电网交换的功率如图2所示.

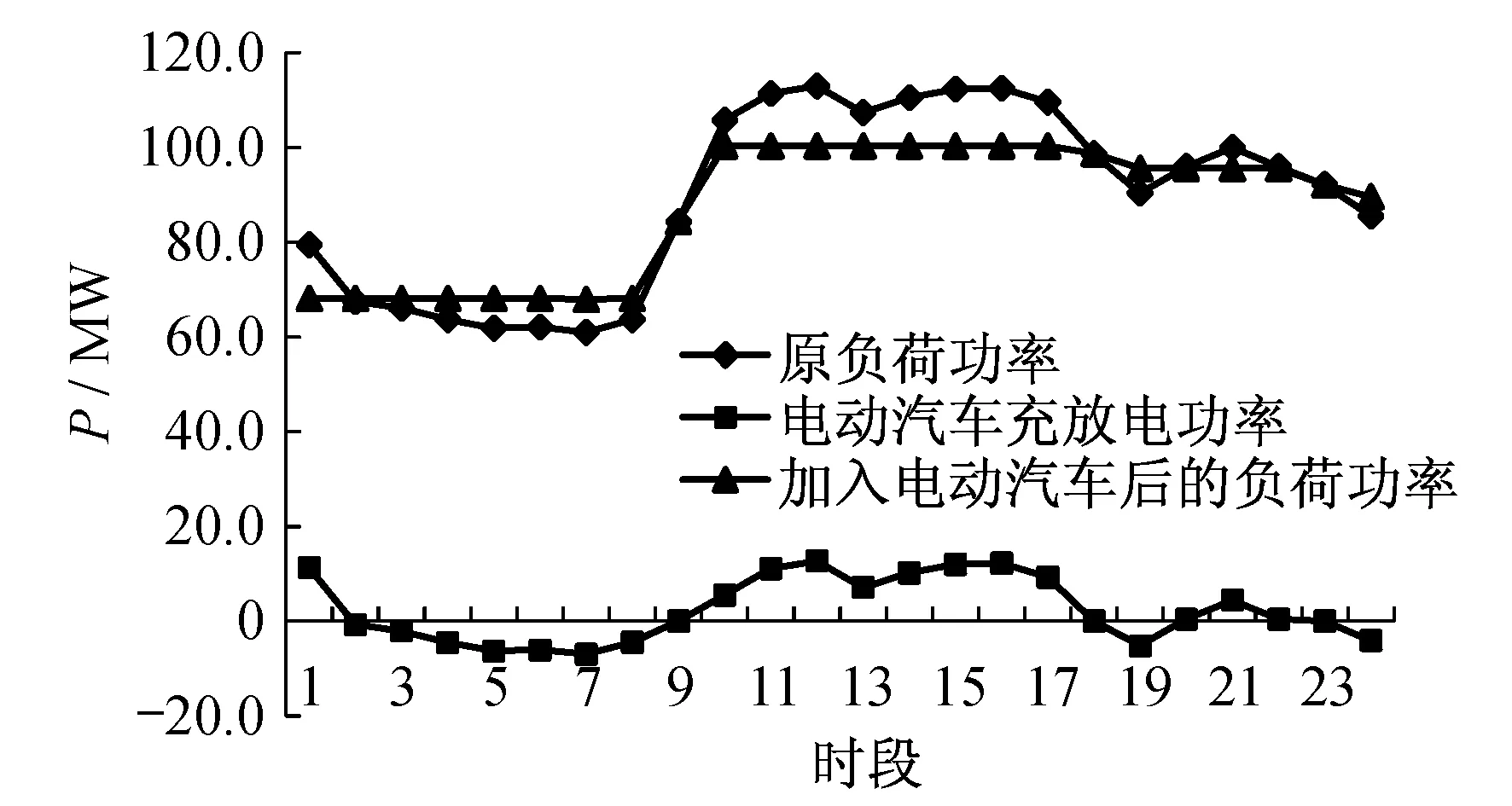
图2 接入电动汽车的变电站日负荷曲线

由图2可以看出,加入了电动汽车充放电功率后,电网负荷曲线变得平坦了.因为有容量和功率约束,电网负荷曲线只是有一定改善.如果没有容量和功率约束,电网负荷曲线将成为一条直线.

此时电动汽车车主的收益为57 279.50元,远远低于以电动汽车车主收益最大为目标函数时的收益.

4.2.2 以电动汽车车主收益最大为目标的优化结果

在目标函数为电动汽车车主收益最大的情况下,通过粒子群算法进行优化计算,电动汽车群作为一个整体在各个时段与电网交换的功率如表3所示.

表3 电动汽车群与电网交换的功率

由表3可以得出如下结论.

(1) 电动汽车群找到了一天中最优的充放电时间组合,响应了电价的波动,从电能交易当中赚取差价利润86 571.71元.

(2) 在电价较高的几个时段(例如9～12,18～21)电动汽车都响应了放电模式,且为最大放电功率;而在电价较低的时段(例如1,2,4)都响应了充电模式,且为最大充电功率,符合让电动汽车在高电价放电、低电价充电的思想,证明该算法适用.

4.2.3 多目标函数优化结果

控制中心首先采集可用电动汽车信息,然后给出最优的功率分配策略.仿真采用粒子群算法.当取不同的权重系数时,得到的结果不同,因此本文分3次取不同的权重系数,结果如图3所示.

将各种权重系数组合的收益计算出来,加入单目标的两种收益,如表4所示.

由图3及表4可以得出如下结论.

(1) 随着权重系数往调峰部分的偏移,变电站负荷曲线越来越平坦,电网的峰谷差很好地被填补,但参与调峰的效果还是没有单独调峰效果明显.

(2) 随着权重系数往收益部分的偏移,电动汽车车主获得的收益越来越大,说明算法合适,结果正确.

(3) 在改变权重系数的值之后,虽然用户获得的利润大幅减少,但调峰效果有显著的改变.因此,引入多个目标函数形成多目标优化,改变各个目标的权重系数可以调整优化结果,优化效果取决于各目标函数的具体特性及权重系数的选择.

图3 多目标下接入电动汽车的变电站日负荷曲线

权重系数组合λ1λ2收益/元1.0057279.500.80.257287.500.50.563293.900.20.881315.8001.086571.71

4 结 语

基于实时电价的电力市场机制,以负荷功率峰谷差最小和电动汽车车主收益最大为目标函数,采用单目标和多目标优化模型,将两个目标取用不同的权重系数.结果表明,可以根据不同的权重系数,协调考虑电网公司调峰效果和电动汽车车主收益大小,从而实现多目标电动汽车控制策略.

如何在现有的优化模型中考虑系统运行条件、网络安全约束和电动汽车群充/放电功率的不确定性是后续要研究的问题.采用有效的求解算法是解决加入不确定性的核心,在后续工作中有待进一步研究.

[1] 高赐威,张亮.电动汽车充电对电网影响的综述[J].电网技术,2011,35(2):127-131.

[2] 胡泽春,宋永华,徐智威,等.电动汽车接入电网的影响与利用[J].中国电机工程学报,2012,32(4):1-25.

[4] 李惠玲,白晓民.电动汽车充电对配电网的影响及对策[J].电力系统自动化,2011,35(17):38-43.

[5] 葛少云,黄镠,刘洪.电动汽车有序充电的峰谷电价时段优化[J].电力系统保护与控制,2012,40(10):1-5.

[6] 韩海英,和敬涵,王小君,等.基于改进粒子群算法的电动车参与负荷平抑策略[J].电网技术,2011,35(10):165-169.

[7] KRISTIEN C N,EDWIN H,JOHAN D.The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J].IEEE Trans on Power Systems,2010,25(1):371-380.

[8] 赵俊华,文福拴,薛禹胜,等.计及电动汽车和风电出力不确定性的随机经济调度[J].电力系统自动化,2010,34(20):22-29.

[9] 王晛,谢鸣,张少华.考虑电动汽车的电力市场均衡分析[J].电网技术,2014,38(11):2 993-2 998.

[10] 杨俊秋.电动汽车充放电容量预测及控制策略的优化研究[D].北京:北京交通大学,2012.

[11] TIAN W Q.HE J H,JIANG J C,etal.The control strategy of V2G participating in peak regulation in power system[C]//Proceedings of 2010 International Conference on Manufacturing Science and Technology.Zibo,China:IEEE,2010.

[12] 田文奇,和敬涵,姜久春,等.基于自适应变异粒子群算法的电动汽车换电池站充电调度多目标优化[J].电网技术,2012,36(11):25-29.

[13] 吕振肃,侯志荣.自适应变异的粒子群优化算法[J].电子学报,2004,32(3):416-420.

(编辑 桂金星)

Research on Multi-target Control Strategy ofEVs Based on Real-time Price

TU Yiyun

(SchoolofElectricalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

A mathematical model is developed on the basis of adopting real-time price in the electricity market and taking into consideration both the profit of power grid and the profit of owners of EVs.The targets of optimization are to minimize the peak-valley difference of power load and maximize the profit of consumer for the participation of EVs in the constraints of battery power and capacity,and solve it by the Particle Swarm Optimization(PSO),and then obtain the power curve between electric vehicles and power grid.Finally,the feasibility and efficiency of the proposed model are verified with the simulation of a given example.

electric vehicle; real-time price; multi-target control strategy

10.3969/j.issn.1006-4729.2016.05.015

2015-06-19

简介：涂轶昀(1978-),女,硕士,讲师,湖北潜江人.主要研究方向为电动汽车入网技术.E-mail: tuyiyunhust@163.com.

U469.72;TP273

A

1006-4729(2016)05-0485-05