风力机流场速度数值模拟

胡丹梅, 郑筱凯

(上海电力学院 能源与机械工程学院, 上海 200090)



风力机流场速度数值模拟

胡丹梅, 郑筱凯

(上海电力学院 能源与机械工程学院, 上海 200090)

为了研究风力机在不同来流风速下和额定风速下运行时的尾流情况,采用数值模拟计算的方法,对美国可再生能源实验室(NREL)5 MW 风力机进行建模并选择不同来流风速进行数值模拟计算.通过模拟计算数据可以看出,风力机下游的风速在0D～4D区域内恢复迅速,在4D～12D区域内恢复缓慢,在12D～16D区域内恢复迅速.其中,在风力机下游6D距离处,来流风速恢复到接近来流风速的60%,在20D处恢复到来流风速的92.8%.由此表明,初始来流风速越大,风力机下游风速越容易恢复到初始风速,并且可以认为在下游20D处下游风力机不再受上游风力机的影响.

风力机; 流场速度; 数值模拟

风力机在风电场中运行时,来流风经过旋转的风轮后,会发生速度与方向的变化,这种风轮对来流风的影响称之为尾流效应[1].由于尾流效应的存在,使得上游风力机对下游风力机的功率输出产生很大影响,同时下游风力机叶片因受到升力、阻力不均匀性的增加,严重影响了风力机的使用寿命[2].对风力机尾流,国内外从实验和数值模拟等方面进行了很多研究.文献[3]和文献[4]利用数值模拟,并结合实地勘测以及风洞试验,对单机流场气动性能进行了全面研究;文献[5]采用滑移网格技术,对一台风力机的气动性能及其尾迹区域的风场特征进行了较为系统的数值模拟;文献[6]利用边界层理念,对风力机尾流进行了数值模拟,模拟结果与风洞实验测量结果相比基本一致;文献[7]和文献[8]针对风速的改变,对风力机尾流不稳定性进行了模拟研究,模拟结果表明,边界层的平均距离是上游风速的函数,该模拟结果与美国可再生能源实验室(NREL)提供的实验数据完全一致.

本文主要用FLUENT软件,基于三维Navier-Stocks控制方程和适用于旋转流场分析的SST k-ω 湍流模型,采用MRF技术对NREL 5 MW 风力机[9]进行了系统模拟,计算了不同来流风速下风力机尾流速度的恢复情况,并将风力机的功率输出与NREL的设计参考数据进行比对,不仅验证了模拟的正确性,而且分析了风力机在不同风速条件下的流场特性,对风力机群的布置有一定的指导作用.此外,本文还分析了额定风速下风力机尾流的影响范围, 以及叶片不同距离处的流线图,发现流体在叶片周围附着流动较好,体现出叶片设计的合理性.

1 数值模拟方法

1.1 控制方程

考虑到风力机是在额定风速下运行,因此计算湍流模型采用具有层流-湍流转捩修正模型的SST k-ω 湍流模型.该模型在近壁面区域有更好的精度和算法稳定性[10-11].其中,粘性不可压缩三维Navier-Stokes方程,基于雷诺时均的连续性方程和动量方程分别为:

(1)

(2)

式中:i,j=1,2,3;ρ——空气的密度,ρ=1.225 kg/m3;μ——动力粘性系数,μ=1.789 4 kg/(m·s).

1.2 风力机的选取

本文选用的NREL 5 MW 风力机,叶片的主要几何参数如表1所示[9].利用FLUENT的前处理软件GAMBIT进行几何建模和网格划分,计算后进行结果分析.

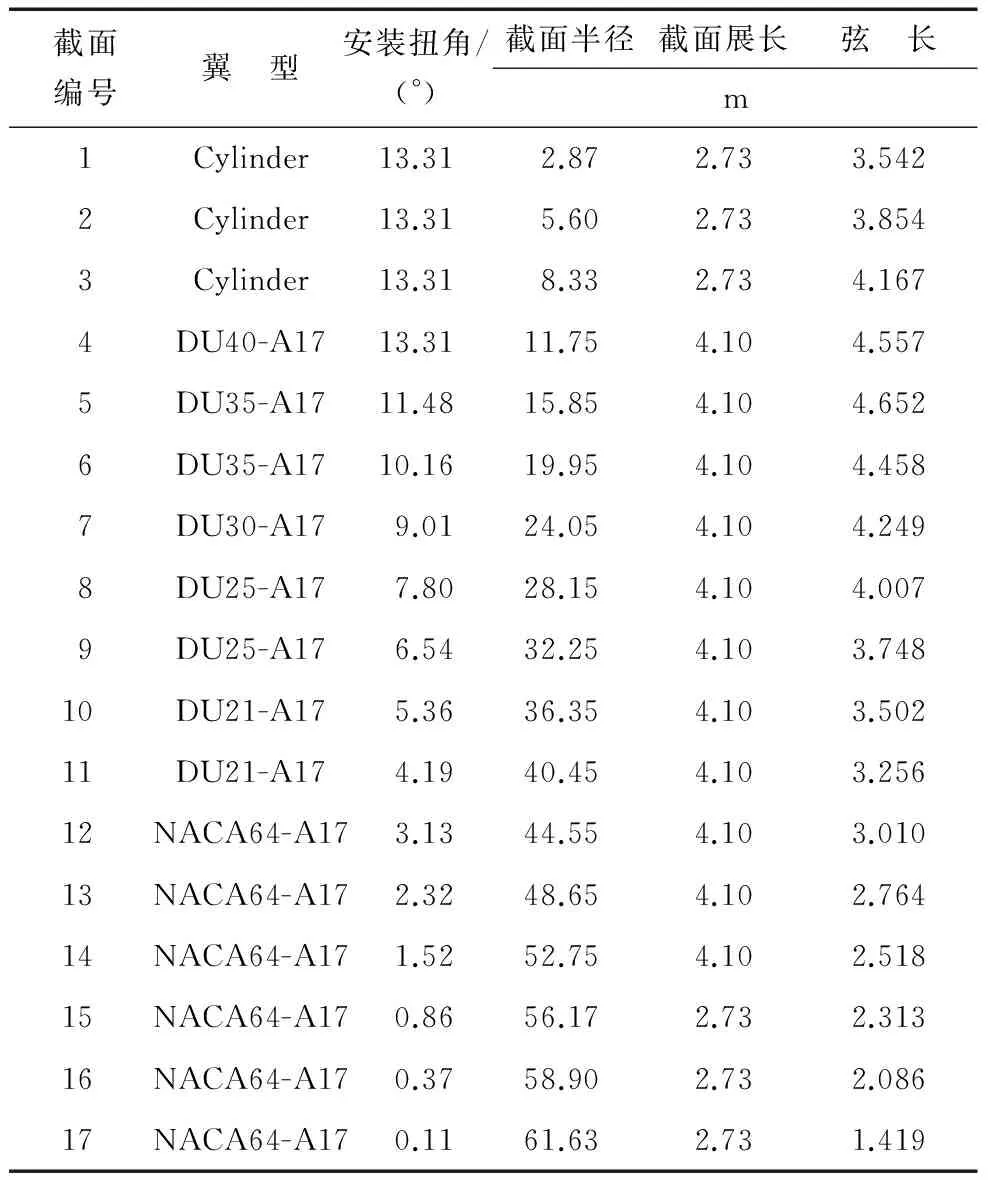
表1 NREL 5 MW风力机叶片几何参数

1.3 边界条件设置

边界条件设置如图1所示.本文采用FLUENT商业模拟软件,设置入口为速度入口,出口为压力出口,旋转小域用MRF方式处理,叶片及轮毂设定为moving wall,近壁面无滑移;计算中所有的交接面用interface处理,其他没有定义的面均为默认wall形式;设置额定来流风速为11.4 m/s,额定转速为12.1 r/min.

图1 边界条件设置示意

1.4 建模及网格划分

图2为风力机建模及流场的网格划分.其中,图2a为单机风轮建模,其叶片长61 m,轮毂简化成一个圆球,半径为3 m,故叶轮直径D=128 m;图2b为旋转小域的网格划分,总网格数为205万个;图2c为整机流场的网格划分,其静止域直径取3D,从风速入口到风力机轮毂中心距离取1D,从风力机轮毂中心到风速出口距离取20D.包围着旋转小域的静止域网格数目为163万个,其后面的静止域网格数目为240万个,整个流场总网格数约为600万个.

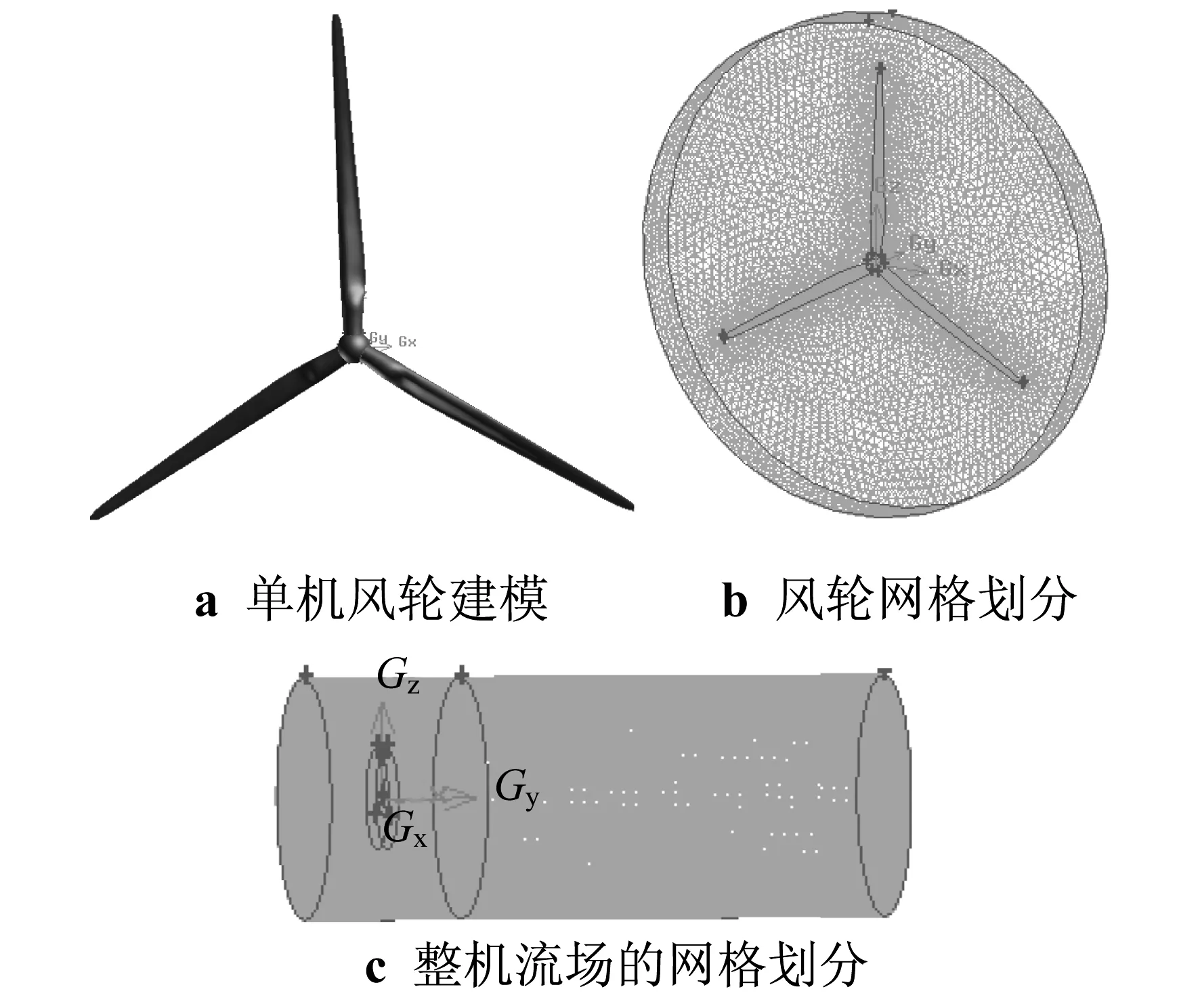
图2 风力机建模及流场的网格划分

本文中风力机需要对旋转小域采用非结构化网格,其中,采用size function的网格划分方法对叶片及轮毂进行网格局部加密处理,叶片表面第一层网格距离叶片表面0.002 m,每层网格增长比率为1.23,最大网格节点尺寸为3.5 m,以此对近壁面进行网格加密处理,近壁面无滑移.流场中其他部分的网格划分相对稀疏,首次计算收敛后采用自适应网格,将湍动能变化梯度较大的部分进行网格加密,以提高求解精度并验证网格无关性.

1.5 网格无关性的验证

待FLUENT迭代收敛后得出转矩,并根据文献[12]给出的公式计算风力机转子的输出功率:

(3)

式中:P——实际输出功率,W;M——转矩,N·m;n——叶轮的转速,r/min;b——叶片数.

得出单机的功率输出后,就可算出其相对误差为:

(4)

式中:γ——相对误差;P0——设计功率,P0=5 MW.

对比旋转小域的网格划分数目,从 124 万计算网格到273 万计算网格在定常条件下的CFD 计算结果,输出功率P相对误差为1.07%～10.96%,如表2 所示.为了减少计算工作量又能得到比较可信的结果,本文选取输出功率P的相对误差在5%以内,旋转小域的网格划分数目为205万个.此时风力机单机输出转矩为3 768 756 N·m,额定转速为12.1 r/min,输出功率为4 775.013 kW,相对误差为4.49%.

表2 网格无关性验证

2 不同风速下模拟的结果分析

2.1 模拟正确性的验证

参照NREL 5 MW 风力机风轮转速随来流风速的变化情况(切入风速6.9 r/min,额定风速12.1 r/min),找出不同风速所对应的风轮转速.本文选择从3 m/s到11 m/s(步长为1)以及额定风速为11.4 m/s的风速,进行模拟计算,模拟结果的功率输出与NREL设计值相比较如图3所示.

图3 风力机输出功率对比曲线

从图3可以看出,虽然数值模拟结果整体上略小于NREL设计数据,但二者在整体变化趋势上却有着良好的一致性.这主要是由于本文为了计算方便,使得网格划分数目不能太多,所以会存在误差.

但是变化趋势的一致性,可以很好地说明本文的数值模拟方法可以正确地分析风力机的三维气动性能,并且可以定性地分析风力机输出功率随来流风速的变化情况,其所获得的定量数值结果对风力机三维气动性能的评估也有着重要的参考价值.

2.2 不同风速下的云图分析

本文选择了来流风速为4 m/s,6 m/s,9 m/s和11 m/s进行模拟分析.图4给出了不同风速条件下,风力机下游不同截面处的最小速度值曲线,风力机下游的截面选择从0D～16D(步长为2D).

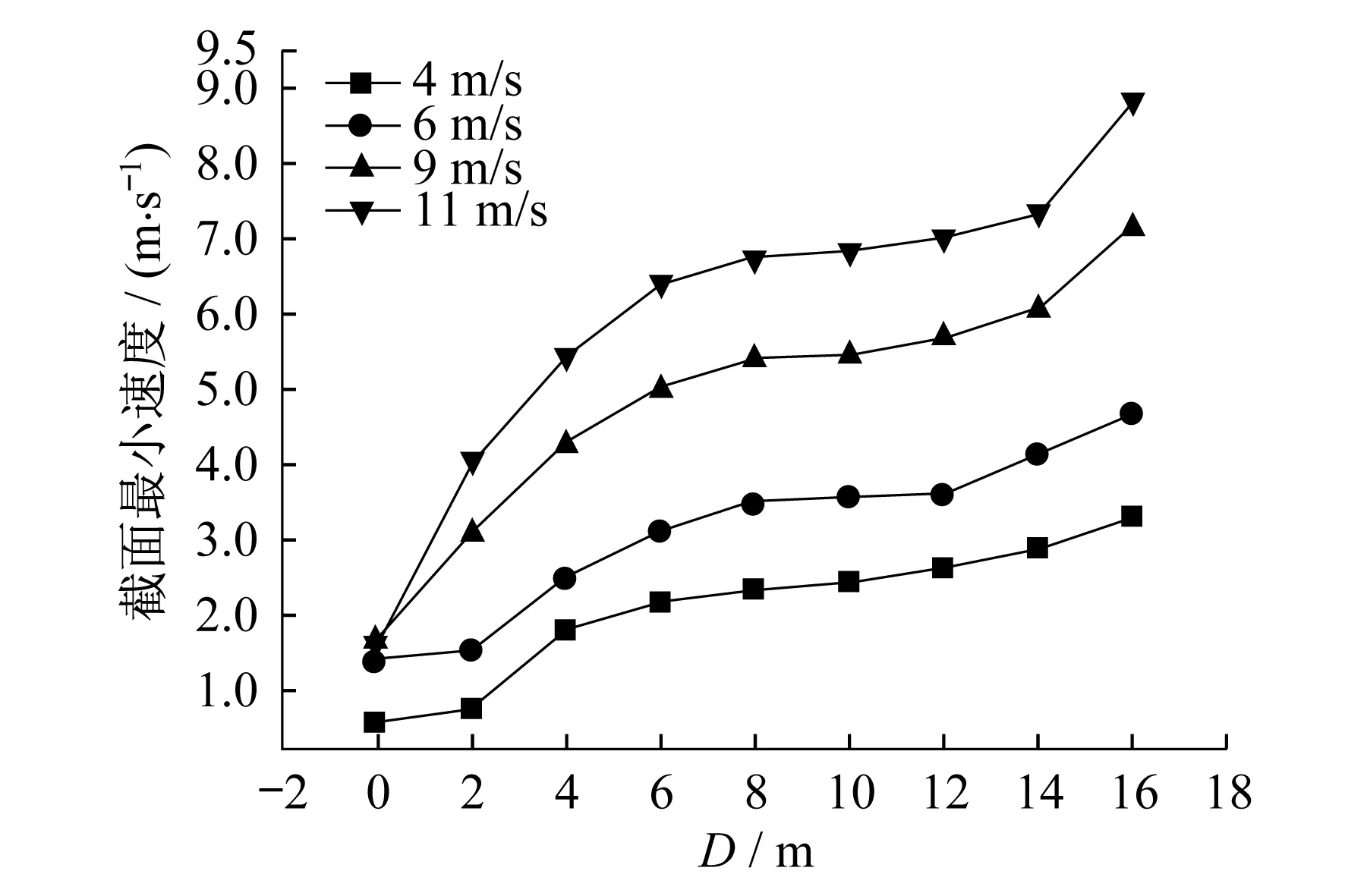
图4 不同来流风速不同截面处速度最小值曲线

从图4可以看出,不管是哪一种来流风速,其在风力机下游的恢复趋势都是一致的.其中,从风力机下游0D～4D部分,速度恢复比较迅速;从4D～12D部分,由于尾流效应的进一步发展,来流风速恢复普遍较为缓慢;从12D～16D部分,由于上游风力机的影响不断减小,其速度恢复开始变得迅速.

图5为不同风速下,在距风力机0D处截面的速度梯度云图.

由图5可知,不同来流风速下,叶轮旋转所形成的速度梯度云图均与轮毂中心对称,并且均在叶尖处存在较大的速度梯度,在叶根处速度梯度较小.这是因为叶尖处翼型比叶根处翼型攻角更大,做功能力更强.此外,从图5还可以看出,来流速度越高,其旋转效应越强.

表3为不同截面处的速度比较.从表3可以看出,来流在风力机处做功,速度大多减小到了初始速度的20%以下.来流风速在距风力机下游4D处迅速恢复,多数恢复到了接近初始速度的50%.而在12D和16D处,11 m/s的来流风速在此处回到了原来速度的63.72%和80.19%,高于其他来流风速在此处的恢复情况,可见初始来流风速越大,在下游越容易恢复到初始速度.

图5 不同风速下0D处截面速度梯度云图

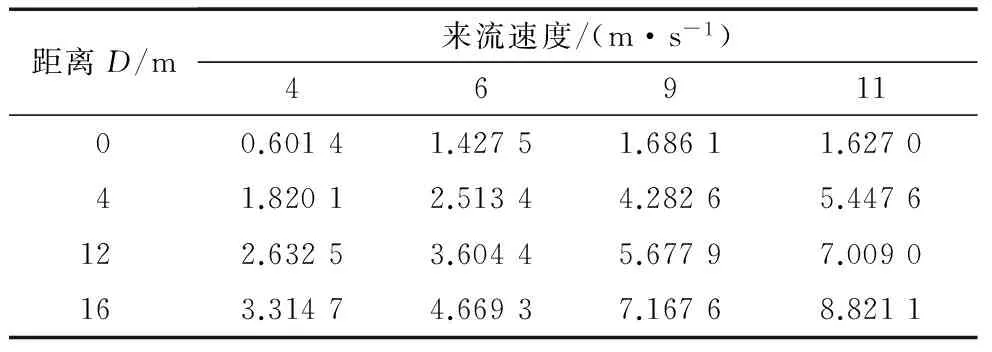
距离D/m来流速度/(m·s-1)4691100.60141.42751.68611.627041.82012.51344.28265.4476122.63253.60445.67797.0090163.31474.66937.16768.8211

3 额定风速下的模拟结果分析

3.1 模拟结果速度分析

图6为下风向从风力机切面到距风力机0D～20D(步长为2D)的速度等值线图和速度云图.从图6可以看出,在6倍风轮直径尾迹区域内,平均风速等值线的分布变化较为剧烈;当尾迹距离达到10D时,平均风速的等值线分布变得稀疏;达到16D时,尾流区域受上游风力机的影响显著减小;当尾迹距离达到20D时,风速已经完全恢复到最初的来流风速.图6b中显示来流风在风力机下游2 500 m处,约为19.5D的距离处,完全恢复了最初的来流风速,与图6a中得到的结论相互呼应.由于风轮旋转带动了气流的旋转,且向下游发展,引起了风力机下游交替出现的低速区域.图6b中显示旋转效应大概在距风力机下游1 900 m处减弱至消失,这与尾流理论相吻合,同时也验证了模拟的合理性.

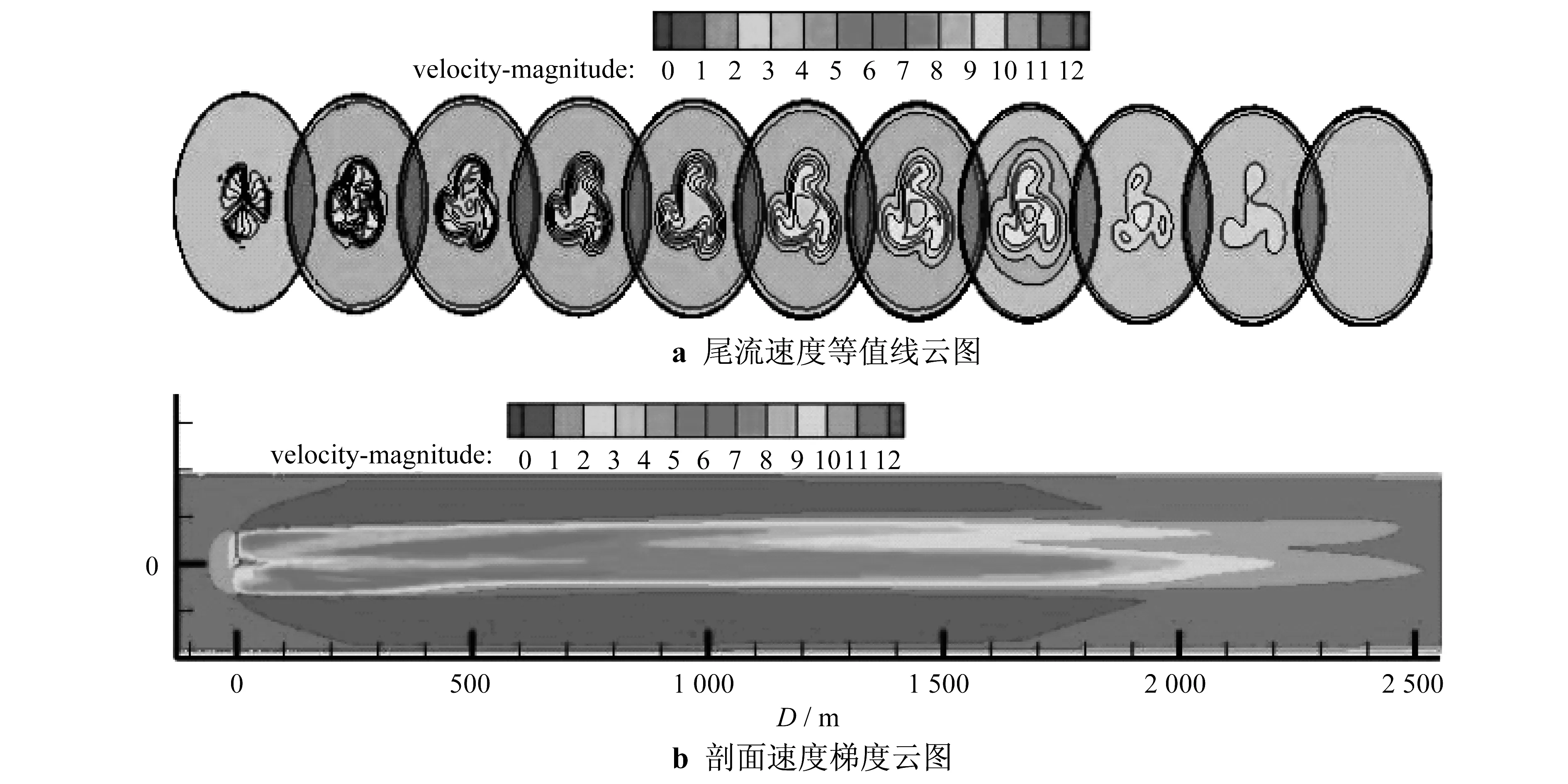
图6 速度梯度云图

图7给出了流场不同截面处的最小速度值.图7中,在-1D(即入口)处,来流风速为额定风速11.4 m/s,在0D处,由于来流推动风力机叶片旋转做功,风速减小至1.55 m/s,仅为额定风速的13.59%.

图7 流场不同截面处最小速度值曲线

风力机下游1D处,来流速度恢复至3.69 m/s,为额定风速的32.37%;风力机下游6D处,来流速度恢复到了6.72 m/s,达到了额定风速的58.95%;10D处,来流速度为7.14 m/s,为额定风速的62.63%,理论上,6D～10D已经可以安置第二台风力机了;16D处,截面速度最小值为9.16 m/s,恢复到额定风速的80.31%,可见此处受风力机的影响已经很小;20D处,截面速度最小值为10.58 m/s,恢复到了额定风速的92.8%,基本可以认为,此处不再受上游风力机的影响.

3.2 叶片不同距离处流线图分析

图8为沿着叶展方向的不同叶片截面处的流线图.图8中,R为叶片半径.图8a为轮毂中心处的截面,明显可以看出流体经过轮毂后,在轮毂的背风处出现了很少量的流动分离,这是因为轮毂为球形,流体的附着流动很好.从图8b到图8d是沿着叶片从叶根指向叶尖方向,0.3R处、0.5R处和0.9R处的剖面流线图可以看到其截面翼型的攻角依次增大.

图8b显示,在叶片的背风处只有一个小型涡存在,在图8c和图8d中叶片背风处的涡依次增大,这是由于其翼型的攻角不断增大,导致叶片背风处的流动分离越来越严重.另外,从图8b可以看到,由于对靠近叶根处的翼型的前缘进行了改善,增加了前缘的厚度,使叶片在攻角很大的情况下,流体依然能够很好地附着流动,体现了叶片设计的合理性.

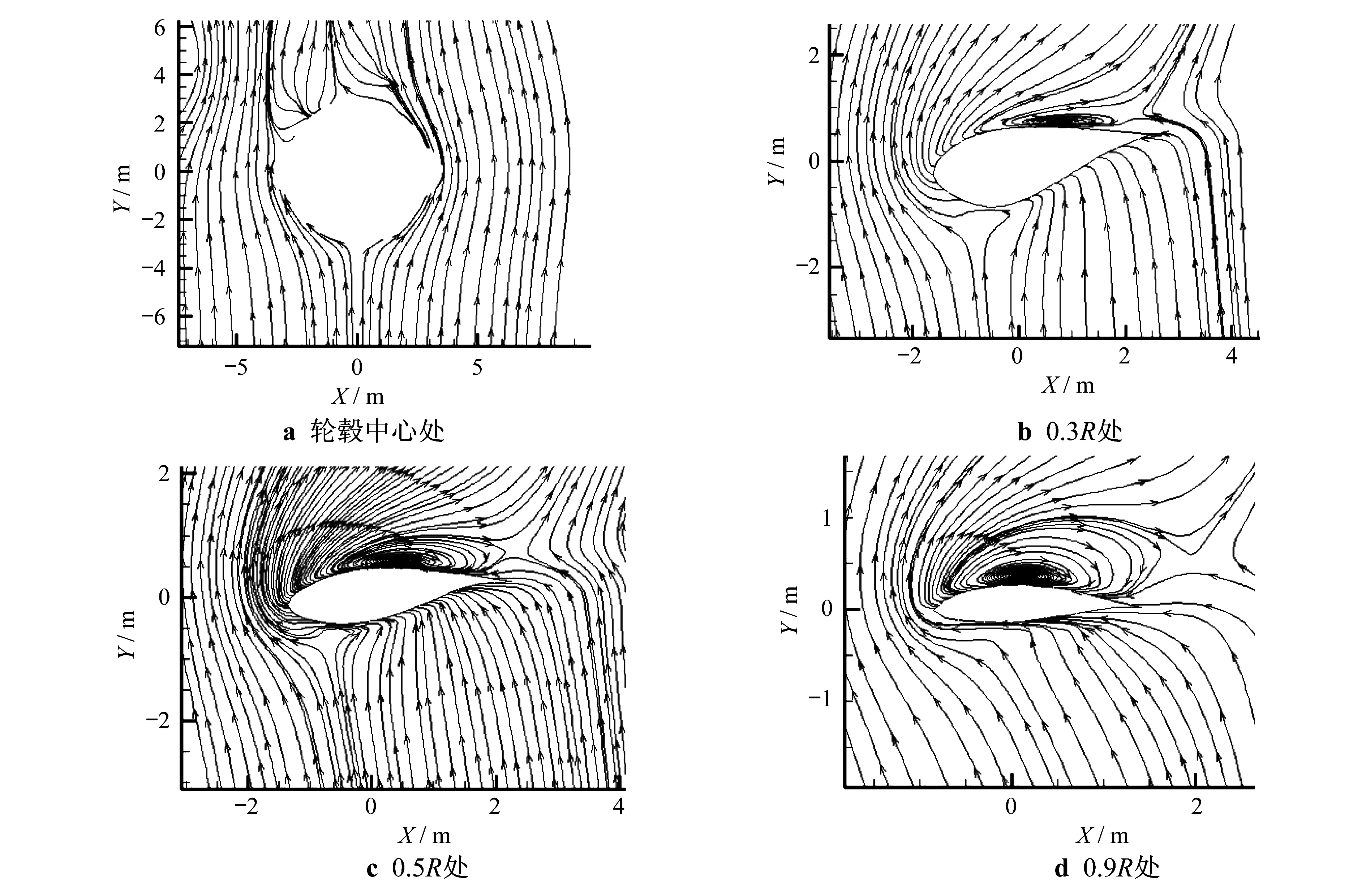
图8 叶片不同截面处流线示意

4 结 论

(1) 通过分析不同来流风速下风力机下游不同截面的速度最小值发现,风力机下游的风速在0D～4D区域内恢复迅速,在4D～12D区域内恢复缓慢,在12D～16D区域内恢复迅速.

(2) 通过比较不同风速下相同截面处的最小速度发现,初始来流风速越大,风力机下游风速越容易恢复到初始风速.

(3) 根据额定风速下风力机的模拟结果速度云图显示,在风力机下游约19.5D处,来流不再受上游风力机的影响.根据所得数据发现,风力机下游6D处,来流风速恢复到接近额定风速的60%,在20D处,来流风速恢复到额定风速的92.8%,基本可以认为此处不再受上游风力机的影响了.

[1] 贾彦,刘璇,李华,等.考虑尾流效应对风电场机组布局的影响分析[J].可再生能源,2014,32(4):429-435.

[2] 韩中合,焦红瑞,李引,等.水平轴风力机尾流特性的数值研究[J].太阳能学报,2011,32(11):1 611-1 615.

[3] BARTHELEMIE R J,RATHMANN O,FRANDSEN S T,etal.Modelling and measurements of wakes in large wind farms[J].Journal of Physics:Conference Series,2007,75(1):12- 49.

[4] CARCANGUI C E.CFD-RANS study of horizontal axis wind turbines[D].Cagliari:Department doing genera mechanical,University deg li Studi di Cagliari,2008.

[5] 任年鑫,欧进萍.大型海上风力机尾迹区域风场分析[J].计算力学学报,2012,29(3):327-332.

[6] AGEL F P,WU Y T,LU H,etal.Conzemius.Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms[J].Wind Eng.Ind.Aerodyn,2011,99(4):154-168.

[7] MO J O,AMANULLAH C,MAZIAR A,etal.Effects of wind speed changes on wake instability of a wind turbine in a virtual wind tunnel using large eddy simulation[J].WindEng.Ind.Aerodyn,2013,117(2):38-56.

[8] UZARRAGE-Rodriguez N, CRISTOBAL Gallegos-Muoz A,MANUEL Riescovila J.Numerical analysis of a rooftop vertical axis wind turbine[C].Proceedings of the ASME 2011 5th International Conference on Energy Sustainability,Washington,DC,USA.August 7-10,2011:795-799.

[9] JONKMAN J,BUTTERFIELD S,MUSIAL W,etal.Definition of a 5-MW reference wind turbine for off shore system development[R].Technical Report NREL/TP-500-38060,2009.[10] MENTER F R,LANGTRY R,VOLKER S.Transition modeling for general purpose CFD codes[J].Flow Turbulence and Combustion,2006,77(1/2/3/4):277-303.

[11] YANG Y,GU M,CHEN S Q,etal.New inflow boundary conditions for modeling the neutral equilibrium atmospheric boundary layer in computational wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics,2009,97(2):88-95.

[12] 何显富,卢霞,杨跃进,等.风力机设计、制造与运行[M].北京:化学工业出版社,2009:189-196.

(编辑 胡小萍)

Numerical Simulation of the Flow Field of Wind Turbine

HU Danmei, ZHENG Xiaokai

(SchoolofEnergyandMechanicalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

In order to study the wake of the wind turbine running in different wind speeds and the rated wind speed,the American Renewable Energy Laboratory(NREL)5MW wind turbine is modeled and simulated at different flow velocity.The data of simulation show that in the downstream 0D～4Darea there can be a rapid recovery of wind speed,and in the 4D～12Darea the wind speed recovers slowly,and in the 12D～16Darea the wind speed recovers rapidly again.In the distance of 6Ddownstream wind speed can recover to about 60% of the initial speed,while in the distance of 20Ddownstream wind speed can recover to 92.8% of the same.The result shows that the downstream wind speed can recover to the initial speed more easily if it has a bigger initial wind speed,and there is no wake effect in about 20Ddownstream.

wind turbine; flow field speed; numerical simulation

10.3969/j.issn.1006-4729.2016.05.001

2015-05-19

简介：胡丹梅(1972-),女,博士,教授,湖南衡南人.主要研究方向为风能利用,动力机械.E-mail:hudanmei @shiep.edu.cn.

国家自然科学基金(50706025); 江苏省水利动力工程重点实验室资助项目(K13024); 上海市教育委员会科研创新重点项目(14ZZ154).

TK83

A

1006-4729(2016)05-0411-06