一类半线性椭圆方程解的幂凹

李丽花

(上海电力学院 数理学院, 上海 200090)



一类半线性椭圆方程解的幂凹

李丽花

(上海电力学院 数理学院, 上海 200090)

研究了一类半线性椭圆方程解的几何性质.通过构造粘性凹包络,以及利用粘性解的性质,得出了半线性椭圆方程解的幂函数是凹函数的结论.并利用方程的解和其水平集之间的关系,证明了解的水平集是凸集.

半线性椭圆方程; 幂凹; 水平集

作为偏微分方程的一个重要研究方向,二阶椭圆方程的解及水平集的性质引起了研究者的广泛关注.在文献[1]中,KOREVAAR N引进了凹极大值原理,并利用该极大值原理和边界点引理证明了推广特征函数方程的解的对数函数为凹函数.KAWOHL B和KENNINGTON A分别减弱了KOREVAAR N极大值原理中的条件,并利用简化的凹极大值原理得到了椭圆方程的解的凸性[2-3].

在文献[4]中,CAFFARELLI L和FRIEDMAN A证明了在二维区域中满足一定条件的椭圆方程的凸解具有常秩的Hessian矩阵.该常秩定理可以和连续性方法结合起来,用来证明解的严格凸性.KOREVAAR和LEWIS给出了n维区域中椭圆方程的常秩定理[5],文献[6]和文献[7]分别给出了复拉普拉斯方程和抛物方程的常秩定理.

在文献[8]中,ALRAVEZ O Z等人通过构造粘性包络来研究椭圆方程的解的凸性.该方法的主要特点是证明方程的解等于它所对应的粘性包络,从而得到原方程的解的凹凸性.利用这种方法,MCCUAN J得到了一类非线性椭圆方程的解的凹性[9].

本文利用构造粘性凹包络的方法,利用粘性解的比较原理,得到了一类半线性椭圆方程的解的幂凹,并证明了解的水平集为凸集,得到了半线性椭圆方程的解的几何性质.

1 粘性凹包及性质

定义1 设Ω为Rn中有界区域,v为定义在Ω上的连续函数,v的凹包络v*定义为:

若存在x∈Ω,使得v(x)=v*(x),则Dv(x1)=…=Dv(xk),且D2v(xi)≤0,i=1,2,3,…,k.

定义2 设Sn为n阶对称矩阵的集合,F为定义在Ω×R×Rn×Sn上的连续函数,若对固定(r,p)∈v(Ω)×Dv(Ω),当A≥B,即A-B半正定时,有:

则称F为椭圆的.

定义3 设φ为定义在Ω上的光滑函数,满足φ≥v*且φ(x)=v*(x),F为椭圆函数,若:

则称v*为椭圆方程F(x,v,Dv,D2v)=0在Ω上的粘性下解.

引理1 设φ为定义在Ω上的光滑函数,φ≥v*且φ(x)=v*(x),I为n阶单位矩阵,有[9]:

2 解的幂凹及水平集的凸性

定理1 设Ω为Rn中有界凸域,n≥2,u为定义在Ω上的光滑函数,且满足方程

(1)

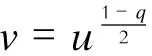
因此,式(1)可化为:

令:

因为v≥0,所以F满足椭圆性条件.构造v的凹包络v*,由定义1可得v*≥v.

设φ为定义在Ω上的光滑函数,满足φ≥v*且φ(x)=v*(x),则有:

(2)

对于式(2)中第一项,由引理1可得:

(3)

利用式(3)和引理2,有:

由此,我们可得:

(4)

因为v(xi)为方程F(x,v,Dv,D2v)=0的解,所以式(4)等于零,故:

又v*(x)≥0,因此:

定理2 设Ω为Rn中有界凸域,n≥2,u为定义在Ω上的光滑函数,且满足方程:

证 明 对于ξ∈(0,1),x1∈Ωc,x2∈Ωc,我们需要证明ξx1+(1-ξ)x2∈Ωc.

利用水平集的定义,可得:

(5)

由式(5)可得:

故ξx1+(1-ξ)x2∈Ωc,即u的水平集Ωc为凸集,定理2证毕.

3 结 语

本文通过构造粘性包络,利用粘性解的比较原理,得到了一类半线性椭圆方程的解的幂凹.并由解的幂凹,证明了解的水平集为凸集,给出了半线性椭圆方程的解的良好的几何性质.

[1] KOREVAAR N.Convex solutions to nonlinear elliptic and parabolic boundary value problems[J].Indiana Univ.Math.J,1983,32(4):73-82.

[2] KAWHOL B.Rearrangements and Convexity of Level Sets in PDE[M].New York:Lectures Notes in Math,Springer-Verlag,1985:31-65.

[3] KENNINGTON A.Power concavity and boundary value problems[J].Indiana Univ.Math.J,1985,34(3):687-704.

[4] CAFFARELLI L,FRIEDMAN A.Convexity of solutions semilinear equations[J].Duke Math J.,1985,52(1):431-456.

[5] KOREVAAR N,LEWIS J.Convex solutions of certain elliptic P.D.E.'s have constant rank Hessians[J].Arch.Rat.Mech.Anal,1987,97(2):19-32.

[6] HAN F,MA X N,WU D M.A constant rank theorem for Hermitian k-convex solutions of complex Laplace equations[J].Meth.Appl.Anal,2009,16(2):263-290.

[7] CHEN C Q,SHI S J.Curvature estimates for the level sets of spatial Quasiconcave solutions to a class of parabolic equations[J].Sci.China.Math,2011,54(10):2 063-2 080.

[8] ALVARE O Z,LASRY J M,Lions P L.Convex viscosity solutions and state constraints[J].J.Math.Pures.Appl,1997,9(3):265-288.

[9] MCCUAN J.Concavity quasiconcavity and quasilinear elliptic equations[J].Taiwanese J.Math,2002,6(2):157-172.

(编辑 白林雪)

Power Concavity of Solutions for a Class of Semilinear Elliptic Equations

LI Lihua

(SchoolofMathematicsandPhysics,ShanghaiUniversityofElectricPower,Shanghai200090,China)

Geometric properties of solutions are investigated for a class of semilinear elliptic equations.Firstly,by constructing viscosity concave envelope and using properties of viscosity solution,power concavity is obtained for the solutions of semilinear elliptic equations.Then,taking advantage of the relationship between the solutions of equations and their level sets,convexity of the level sets is proved.

semilinear elliptic equation; power concavity; level set

10.3969/j.issn.1006-4729.2016.05.020

2015-09-02

简介：李丽花(1979-),女,博士,副教授,江西上饶人.主要研究方向为系统分析与集成.E-mail:dlxyllh2004@163.com.

O175.25

A

1006-4729(2016)05-0507-03