考虑网络损耗的节能发电调度模型及其混合整数二次规划算法

黄缙华, 顾博川, 唐升卫, 尤毅，刘菲，夏亚君

(广东省智能电网新技术企业重点实验室(广东电网有限责任公司电力科学研究院)，广东 广州510080)



考虑网络损耗的节能发电调度模型及其混合整数二次规划算法

黄缙华, 顾博川, 唐升卫, 尤毅，刘菲，夏亚君

(广东省智能电网新技术企业重点实验室(广东电网有限责任公司电力科学研究院)，广东 广州510080)

首先,提出一种非凸的节能发电调度模型，该模型考虑了火电机组的发电阀点效应、直流潮流、线路的安全传输容量约束和网络损耗；然后,运用线性近似和混合整数编码技术处理非光滑的目标函数和网络损耗，并将直流潮流和线路的安全传输容量约束表示为线性约束，从而将非凸的节能发电调度模型转化为混合整数二次规划模型；最后，通过IEEE-30节点系统、IEEE-118节点系统和波兰2746节点系统测试所提模型和方法，并与直流最优潮流模型和交流最优潮流模型的仿真结果进行比较。对比结果验证了所提模型和方法在节能发电调度中的有效性。

节能发电调度；混合整数二次规划；安全约束；直流潮流；网络损耗

在日前发电调度计划问题中，很多学者的研究重点为从电厂侧确定节能发电调度计划[1-6]，而缺乏考虑电网侧的网络损耗。网络损耗作为影响节能发电调度的一个重要因素，理应在实际调度中加以考虑[7-10]。很多研究在考虑电力网络时，把线性形式的直流潮流方程整合到发电调度模型中，此种方法简单易行，但模型未考虑网络损耗，因此模拟实际调度情况的精度不高[11-12]。基于分离迭代的方法，在采用直流潮流的同时，将网络损耗独立分离出来并通过迭代求解，该方法效率高，但只能找到次优解[7]。

为了有效考虑网络损耗对发电调度计划的影响，可以根据调度员的经验把网络损耗以一定比例折算到负荷中，该方法易于实现但误差较大。基于B矩阵的网络损耗计算方法能够较好地模拟网损，但需要随着负荷和系统运行方式的改变而相应调整矩阵系数，因此实用性不强[1]。具有非线性形式的交流潮流能够精确计算网络损耗，但在日前发电调度计划中，网络节点的无功负荷往往难以预测，导致无法直接应用交流潮流计算网损。交流最优潮流(AC-optimalpowerflow，AC-OPF)也是一种能够精确模拟网络损耗的方法[13]，该方法同样依赖于调度周期内的无功负荷预测值，且文献[8]指出：由于实际工程对非线性规划方法的限制，比如鲁棒性要求，AC-OPF在日前发电调度中仍存在困难。

针对计及网络损耗的日前发电调度计划问题，文献[7]提出了一种动态分段线性模型求解含二次线路损耗约束的最优发电调度问题，该模型通过动态迭代的方式更新线性化的线路损耗，直到线性近似的误差满足收敛精度。文献[8]通过松弛的方式将二次等式的线路损耗约束化为不等式约束，对于不满足等式的线路损耗约束，引入线路损耗变量，并通过惩罚的方式添加到目标函数中。上述两种方法都能较好地处理二次的线路损耗约束，但当系统存在负节点边界成本时，文献[7]的动态分段线性模型需要针对线路损耗约束增加额外的线性约束限制问题的可行区域，文献[8]的方法则需要通过惩罚的方式使线路损耗约束满足等式要求。此外，上述方法处理的模型常将目标函数简化为二次函数或分段线性函数，以此保证该模型目标函数可微分。但是，在实际运行中，受汽机阀门状态的影响，火电机组的发电煤耗曲线呈现出不可微分的特性，即火电机组的发电阀点效应[10,14]，从而导致常用的数学规划方法无法直接求解包含该类非凸目标函数的节能发电调度问题。

为了有效处理考虑网络损耗和火电机组发电阀点效应的节能发电调度问题，本文在确定机组开停状态的前提下，提出一种基于混合整数二次约束二次规划的节能发电调度算法，该算法既能够有效处理非凸的目标函数，也考虑线路的安全传输容量约束和网络损耗。

1 直流潮流、线路传输容量约束和网损

1.1 直流潮流

对于节点i至节点j的第l条线路，以流出节点的功率方向为正方向，则有：

式中：Pl,ij为线路l由节点i至节点j的有功功率，Ui、Uj分别为节点i、节点j的电压幅值，θij为节点i的电压与节点j的电压的相位差，Gij、Bij分别为节点i至节点j的线路电导和电纳。

工程上将正常运行时线路两端节点的电压标幺值看作1，并认为线路两端的电压相位差很小，则式(1)的正弦项和余弦项可近似为：

将式(1)中的第一项减去第二项，可得系统的直流潮流方程为

式中：Rij、Xij分别为节点i至节点j的线路电阻和电抗，且Rij≪Xij。

1.2 线路传输容量约束

由于每条线路的线损较小，因此线路的安全传输容量可近似处理为线路两端功率之差的均值，则线路的传输容量约束为

1.3 线路损耗

将式(1)中的两项相加，可得线路的损耗

2 非凸的节能发电调度模型

2.1 目标函数

在本文的节能发电调度模型中，以总发电煤耗成本最小为目标，数学表达式为

式中：F为总发电煤耗成本，Fi为第i台火电机组的发电煤耗成本，Pi为第i台火电机组的发电出力，N为总发电机组数量。

在调度精度要求不高的情况下，每台发电机组的出力-煤耗成本曲线可以用二次函数描述，即

(2)

式中ai、bi、ci均为第i台火电机组的发电成本系数。

在实际运行中，汽轮机调门处于阀点状态时，汽轮机热耗率相对较低，这使得机组的出力-煤耗成本曲线在相应的出力点上变得不光滑，这种现象称为火电机组的发电阀点效应。当计及火电机组的发电阀点效应时，每台机组的出力-煤耗成本曲线函数为

(3)

式中：ei、fi均为第i台火电机组的发电成本系数，Pi,min为第i台火电机组的出力下界。

计及发电阀点效应的非光滑火电机组出力-煤耗成本曲线及其线性化如图1所示。

图1 非光滑火电机组的出力-煤耗成本曲线及其线性化处理

2.2 约束条件

2.2.1 节点功率平衡约束

式中：Gi、Li、Di分别为节点i的火电机组集合、线路集合和负荷集合，NB为总节点数量，PDk为连接到节点i的第k个负荷。

2.2.2 直流潮流约束

(4)

式中NL为总线路数量。

2.2.3 线路的安全传输容量约束

2.2.4 线路损耗约束

2.2.5 参考母线电压相位约束

式中：θi、θj分别为节点i、节点j的电压相位，θref为参考节点的电压相位。

2.2.6 火电机组的爬坡约束

式中：vdi、vui分别为第i台火电机组的降出力速率和升出力速率，P0,i为第i台火电机组的初始出力。

2.2.7 机组出力容量约束

式中Pi,max为第i台火电机组的出力上界。

2.3 模型特性分析

在本文的考虑网络损耗的非凸节能发电调度模型中，主要存在两个难点：一是更精确、非光滑的火电机组出力-煤耗成本曲线，二是线路损耗约束。

引入火电机组的发电阀点效应，有助于提高节能发电调度模型的精度，但使得该模型成为一个非凸的优化模型。传统的基于梯度的数学规划式方法要求目标函数满足可微分的条件，火电机组的发电阀点效应导致目标函数存在不可微分点，从而使得大多数的数学规划式方法无法直接求解该模型[15]。值得注意的是，非光滑出力-煤耗成本曲线中的不可微分点，往往导致优化模型中出现大量的局部最优点，且局部最优点的数量随着不可微分点的增加呈指数型增长[16]。因此，在设计算法求解该模型时，需要合理分析该模型目标函数的非光滑特性，采用有效的应对措施。

在本文提出的模型中，除了线路损耗约束，其他约束都为线性约束。在忽略火电机组的发电阀点效应的前提下，将二次的线路损耗约束看作非线性约束，本文提出的模型为一个含二次等式约束的非线性模型，可通过内点法等非线性规划算法进行求解。但是，这种处理方式的节能效果较差。基于动态分段线性模型[7]和基于松弛技术的二次规划二次约束模型[8]能够较好地处理二次的线路损耗约束，但在同时考虑火电机组的发电阀点效应时，两者都无法直接适用。

为了同时考虑非光滑的出力-煤耗成本曲线和二次的线路损耗约束，本文采用线性近似和混合整数编码技术，把出力-煤耗成本曲线和线路损耗约束化为线性的形式，从而将非凸的节能发电调度模型转化为一个混合整数凸规划模型。

3 混合整数二次规划优化算法

3.1 线性化非光滑出力-煤耗成本曲线

如图1所示，对于考虑发电阀点效应的火电机组，线性化非光滑的出力-煤耗成本曲线后，可得到

式中：Mi为火电机组i的线性分段数量；Kij和Wij分别为火电机组i的线性分段j的斜率和截距；Zij为二进制变量，且对应火电机组i的第j个子连续分量Pij。

Mi可以根据以下公式求取：

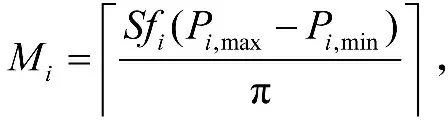
式中S为正弦波在半个周期内的线性分段数量。

Kij和Wij可以根据以下公式求取：

式中Plb,ij和Pub,ij分别为机组i的线性分段j的出力下界和上界。

Plb,ij和Pub,ij可以根据以下公式求取：

对非光滑出力-煤耗成本曲线进行线性化处理后，为了保证火电机组的出力只处于某一个线性分段对应的范围内，需要增加以下约束：

(6)

在式(6)中，第2项和第3项确保当火电机组的出力位于某一个线性分段时，对应的二进制变量为1，其他线性分段对应的二进制变量和子分量都为零，因此机组的出力可以写成各个子分量之和。

3.2 线路损耗的线性近似

由于每条线路的损耗表示为该线路两端电压相位差的二次函数，因此可以通过静态线性近似的方式将二次线路损耗约束化为线性约束，即

式中：Rl为线路l两端电压相位差的线性分段数量；kl,r和bl,r分别为线路l线性分段r的斜率和截距；Ul,r为二进制变量，且对应线路l的损耗子分量θl,r。

在线性化二次线路损耗约束后，线路l两端的电压相位差必须位于其中一个线性分段对应的相位范围内。为了保证上述条件的成立，需要增加以下约束：

式中θlb,r,l和θub,r,l分别为线路l线性分段r的相位差下界和上界。值得注意的是，kl,r、bl,r、θlb,r,l和θub,r,l的计算方式与处理非光滑目标函数时相似。

3.3 混合整数二次规划模型

为了简化考虑网络损耗的非凸节能发电调度模型，本文把直流潮流约束式(4)代入线路的安全传输容量约束式(5)，从而消去线路的安全传输容量约束，得：

(7)

根据式(7)和θij的上、下界，可以得到

式中θij,max、θij,min分别为线路l两端电压相位差的上、下界。

在线性化非光滑的出力-煤耗成本曲线和二次的线路损耗约束后，非凸的节能发电调度模型被转化为一个混合整数二次规划模型。数学表达式为：

式中：H和f分别为目标函数的系数矩阵和系数向量，A和b分别为线性不等式约束的系数矩阵和系数向量，Aeq和beq分别为线性等式约束的系数矩阵和系数向量，lb和ub分别为决策变量的上、下界向量，X为混合整数二次规划模型中的决策变量向量，xj为二进制变量。

4 算例分析

4.1 算例描述和参数设置

本文通过IEEE-30节点系统、IEEE-118节点系统和波兰2746节点系统验证所述模型和方法的有效性。对于上述3个系统，每条线路两端的电压相位差用弧度表示，且范围都为[-0.5，0.5]。

本文采用CPLEX软件的混合整型规划(mixedintegerprogramming，MIP)求解器对所得的混合整数二次规划(mixedintegerquadraticprogramming，MIQP)模型进行求解。直流最优潮流(DC-optimalpowerflow，DC-OPF)模型和AC-OPF模型的求解方法分别为MATLABR2013b软件中的线性规划方法和内点法。所有算例都在MATLAB软件上编码，仿真计算的硬件平台为一台内存4GiB、频率3.10GHz的台式计算机。

需要说明的是，本文以AC-OPF模型作为结果对比的基准。在衡量DC-OPF模型和本文所述模型的网络损耗不平衡量误差时，分别计算如下[8]：

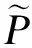
4.2 IEEE-30节点系统

为了验证所述模型和方法的有效性，本文首先在IEEE-30节点系统上进行测试。在该测试系统中，采用Matpower4.1软件中IEEE-30节点系统的成本系数作为火电机组的二次出力-煤耗成本曲线的系数。

通过MIQP方法求解所述的节能发电调度模型，并与DC-OPF方法和AC-OPF方法进行对比，结果见表1。

表1 3种模型在IEEE-30节点系统的结果比较

模型总发电成本/美元总发电量/MW网络损耗/MW网损不平衡量误差/%DC-OPF565.21189.201.470AC-OPF576.89192.12.86MIQP576.17192.12.850.005

为了保证模拟线路损耗的近似精度，在该系统中，每条线路两端的电压相位差的线性分段数量设置为一个较大的数值。由表1可知：本文提出的MIQP模型在总发电成本、总发电量和网络损耗方面都与AC-OPF模型的结果相近；与MIQP模型相比，由于DC-OPF模型忽略线路损耗，因此所得的结果与基准结果相比存在较大的误差。

基于线性近似和混合整数编码技术，本文所得的MIQP模型为一个凸规划模型，在给定非光滑目标函数和每条线路两端电压相位差的线性分段数量的情况下，本文的模型能够得到唯一的全局最优解。值得注意的是，与求解AC-OPF模型的原对偶内点法相比，本文所述的MIQP方法不依赖于初始点的选取，因此具有更好的鲁棒性能。

4.3 IEEE-118节点系统

本文通过IEEE-118节点系统验证所述模型和方法的可拓展性。该系统的拓扑数据和负荷数据来自Matpower4.1软件中的IEEE-118节点系统，根据煤耗成本折算的火电机组出力-成本系数来自文献[17]。

值得注意的是，该系统中8台火电机组具有非凸的出力-煤耗成本曲线，导致DC-OPF模型和AC-OPF模型都无法直接求解该非凸模型。因此，本文通过AC-OPF模型和DC-OPF模型求解该非凸模型时，首先采用式(2)的目标形式，在求解出各台火电机组的出力情况后，再通过式(3)求解最终的目标函数值。

表2对MIQP模型、DC-OPF模型和AC-OPF模型求解IEEE-118节点系统的结果进行了对比。

表2 3种模型在IEEE-118节点系统的结果比较

由表2可知，与DC-OPF模型相比，由MIQP模型求得的结果在总发电成本、总发电量和网络损耗方面都与AC-OPF模型的结果更接近；在网络损耗不平衡量的误差方面，MIQP模型的结果为0.60%，远小于DC-OPF模型的1.68%，此结果有效验证了本文提出的模型能够得到更合理的网络损耗。

4.4 波兰2746节点系统

为了验证本文所述方法的拓展性，在波兰2746节点实际系统上进行测试。DC-OPF、AC-OPF和MIQP 3种模型在该系统的对比结果见表3。

表3 3种模型在波兰2746节点系统的结果比较

模型总发电成本/万美元总发电量/GW网络损耗/MW网损不平衡量误差/%DC-OPF158.14250524.873020.00001.94AC-OPF163.17751025.36473491.7090MIQP158.74142325.31009437.07470.22

由表3可知，与DC-OPF模型相比，MIQP模型在总发电成本、总发电量和网络损耗都与AC-OPF模型的结果更接近，且MIQP模型的网损不平衡量误差约为0.22%，显著优于DC-OPF模型。在波兰2746节点系统的仿真结果有效验证了本文所述方法在求解大规模系统时的可拓展性，并能较为准确地模拟网络损耗。

4.5 MIQP模型在不同负荷水平下的鲁棒性

为了进一步验证本文所述模型和方法的有效性，本文以Matpower4.1软件中的IEEE-118节点系统的负荷水平为基准，在0.7～1倍基准负荷之间，随机产生5种负荷情景，然后通过MIQP模型、DC-OPF模型和AC-OPF模型进行求解。3种模型的结果比较见表4。

从表4可以看出，对于上述随机产生的5种负荷情景，本文提出的MIQP模型都能够得到稳定的结果；与DC-OPF模型相比，MIQP模型在总发电成本、总发电量和网络损耗方面更接近作为基准的AC-OPF模型的结果；在网络损耗不平衡量的误差方面，MIQP模型的结果明显优于DC-OPF模型。可见，上述结果有效验证了本文所述模型和方法的鲁棒性。

表4 3种模型在IEEE-118节点系统不同负荷情景下的结果比较

情景模型总发电成本/万美元总发电量/GW网络损耗/MW网损不平衡量误差/%DC-OPF5.3249343.57170.001.541AC-OPF5.4591803.628456.70MIQP5.5307003.651579.760.63DC-OPF5.4218453.62550.001.522AC-OPF5.5440133.682356.79MIQP5.6167673.704679.110.60DC-OPF5.4304653.63040.001.563AC-OPF5.5605903.688958.47MIQP5.6280303.711781.340.61DC-OPF5.4114873.62000.001.564AC-OPF5.5417923.678258.20MIQP5.6111793.701081.070.61DC-OPF5.4829363.65710.001.665AC-OPF5.6080593.719762.66MIQP5.6788233.741984.830.59

5 结论

本文提出一种考虑网络损耗的节能发电调度模型，并通过MIQP优化算法进行求解。基于本文的算例仿真分析，得到如下结论：

a) 在建立节能发电调度模型时，有必要考虑电网侧的安全约束和网络损耗，并考虑火电机组的发电阀点效应，一方面保证节能发电调度的安全性，另一方面使所建立的模型更贴合实际调度的情况。

b) 本文通过线性近似和混合整数编码技术将非凸的节能发电调度模型化为MIQP模型，大大降低了模型的求解难度，且具有良好的鲁棒性。

c) 与DC-OPF模型相比，MIQP模型的结果更接近AC-OPF模型的结果。与AC-OPF模型相比，本文所述模型的求解方法不依赖于初始点的选取，且能够保证解的唯一性。

[1] 赵维兴, 林成, 孙斌,等.安全约束条件下综合煤耗最优的节能调度算法研究[J].电力系统保护与控制, 2010, 38(9)：18-22.

ZHAO Weixing，LIN Cheng，SUN Bin，et al.A Security-constrained Energy-saving Dispatch Algorithm for Optimal Integrated Coal Consumption[J].Power System Protection and Control，2010，38(9)：18-22.

[2] 吕素, 黎灿兵, 曹一家,等.基于等综合煤耗微增率的火电机组节能发电调度算法[J].中国电机工程学报, 2012, 32(32)：1-7.

LÜ Su, LI Canbing, CAO Yijia, et al.An Energy-saving Generation Dispatch Algorithm for Thermal Generators Based on the Integrated Equal Coal-consumption Increment[J].Proceedings of the CSEE，2012，32(32)：1-7.

[3] 张宁, 陈慧坤, 骆晓明,等.广东电网节能发电调度计划模型与算法[J].电网技术, 2008, 32(24)：11-15.

ZHANG Ning, CHEN Huikun, LUO Xiaoming, et al.Energy-saving Generation Dispatch Scheduling Model and Algorithm for Guangdong Power Grid[J].Power System Technology，2008，32(24)：11-15.

[4] 陈之栩，谢开，张晶，等.电网安全节能发电日前调度优化模型及算法[J].电力系统自动化，2009，33(1)：10-13.

CHEN Zhixu，XIE Kai，ZHANG Jing，et al.Optimal Model and Algorithm for Day-ahead Generation Scheduling of Transmission Grid Security Constrained Convention Dispatch[J].Automation of Electric Power Systems，2009，33(1)：10-13.

[5] 黎灿兵，尚金成，李响，等.集中调度与发电企业自主调度相协调的节能调度体系[J].中国电机工程学报，2011，31(7)：112-118.

LI Canbing，SHANG Jincheng，LI Xiang，et al.Novel Energy-saving Generation Dispatch System Based on the Coordination of Centralized Dispatch and Decentralized Dispatch of Power Generation Enterprises[J].Proceedings of the CSEE，2011，31(7)：112-118.

[6] 林玥廷，向德军，徐晓亮，等.计划安全校核在实时节能发电调度中的应用[J].广东电力，2014，27(9)：63-67.

LIN Yueting, XIANG Dejun, XU Xiaoliang, et al.Application of Planning Safety Check in Real-time Energy Saving Generating Dispatching[J].Guangdong Electric Power, 2014,27(9)：63-67.

[7] SANTOS T N D, DINIZ A L.A Dynamic Piecewise Linear Model for DC Transmission Losses in Optimal Scheduling Problems[J].IEEE Transactions on Power Systems, 2011, 26(2)：508-519.

[8] ZHONG H, XIA Q, WANG Y, et al.Dynamic Economic Dispatch Considering Transmission Losses Using Quadratically Constrained Quadratic Program Method[J].IEEE Transactions on Power Systems, 2013, 28(3)：2232-2241.

[9] WANG S J, SHAHIDEHPOUR S M, KIRSCHEN D S, et al.Short-term Generation Scheduling with Transmission and Environmental Constraints Using an Augmented Lagrangian Relaxation[J].IEEE Transactions on Power Systems,1995, 10(3)：1294-1301.

[10] WANG M Q, GOOI H B, CHEN S X, et al.A Mixed Integer Quadratic Programming for Dynamic Economic Dispatch with Valve Point Effect[J].IEEE Transactions on Power Systems, 2014, 29(5)：1-10.

[11] CONEJO A J, AGUADO J A.Multi-area Coordinated Decentralized DC Optimal Power Flow[J].IEEE Transactions on Power Systems, 1998, 13(4)：1272-1278.

[12] LI Z, WU W, ZHANG B, et al.Decentralized Multi-area Dynamic Economic Dispatch Using Modified Generalized Benders Decomposition[J].IEEE Transactions on Power Systems, 2016, 31(1)：526-538.

[13] CHUNG C Y, YAN W, LIU F.Decomposed Predictor-Corrector Interior Point Method for Dynamic Optimal Power Flow[J].IEEE Transactions on Power Systems, 2011, 26(3)：1030-1039.

[14] CHIANG C L.Improved Genetic Algorithm for Power Economic Dispatch of Units with Valve-point Effects and Multiple Fuels[J].IEEE Transactions on Power Systems, 2005, 20(4)：1690-1699.

[15] WOOD A J, WOLLENBERG B F.Power Generation, Operation, and Control[M].New York：Wiley, 1984.

[16] ZHAN J, WU Q H, GUO C, et al.Economic Dispatch with Non-smooth Objectives—Part I：Local Minimum Analysis[J].IEEE Transactions on Power Systems, 2015, 30(2)：710-721.

[17] The Data of Non-smooth Cost Functions[EB/OL].[2016-06-21].http：//motor.ece.iit.edu/data/IEEE118bus_inf/.

(编辑 李丽娟)

Energy-saving Generation Dispatching Model Considering Transmission Losses and Its Mixed Integer Quadratic Programming

HUANG Jinhua, GU Bochuan, TANG Shengwei, YOU Yi, LIU Fei, XIA Yajun

(Guangdong Province Key Laboratory of Smart Grid Technology, Electric Power Research Institute of Guangdong Power Grid Co., Ltd., Guangzhou, Guangdong 510080, China)

This paper firstly presents a non-convex energy-saving dispatching model considering generation valve point effect, DC power flow, security transmission capacity constraints of lines and transmission losses.Then, it uses linear approximation and mixed integer coding technology to deal with non-smooth objective target function and transmission losses, as well as represents DC power flow and security transmission capacity constraints of lines as linear constraints so as to convert the non-convex energy-saving generation dispatching model into a mixed integer quadratic programming model.Finally, it tests proposed models and methods by employing IEEE-30 node system, IEEE-118 node system and Polish 2746 node system, and compares simulation results with those of DC and AC optimal power flow models.Comparison results verify validity of proposed models and methods in energy-saving generation dispatching.

energy-saving generation dispatching; mixed integer quadratic programming; security constraint; DC power flow; transmission loss

2016-06-21

2016-07-28

广东省智能电网新技术企业重点实验室资助项目(2060299)；中国南方电网有限责任公司科技项目(GDKJ00000063)

10.3969/j.issn.1007-290X.2016.11.018

TM734

A

1007-290X(2016)11-0093-07

黄缙华(1986)，男，湖南永州人。工程师，工学硕士，主要从事电网调度自动化的研究工作。

顾博川(1985)，男，黑龙江密山人。工程师，工学硕士，从事调度自动化和配电技术的研究工作。

唐升卫(1986)，男，湖南衡阳人。工程师，工学硕士，从事调度自动化和负荷调度技术的研究工作。