直埋单芯电缆载流量仿真方法研究及其应用

李文沛

(深圳供电局有限公司，广东 深圳 518001)



直埋单芯电缆载流量仿真方法研究及其应用

李文沛

(深圳供电局有限公司，广东 深圳 518001)

当前通常采用IEC 60287标准推荐方法对电缆载流量进行计算，但在工程实际中，发现该方法计算结果与实际情况有一定差距。以直埋敷设条件下的110 kV 高联聚乙烯(cross-linked polyethylene,XLPE)电缆为研究对象，建立了磁热耦合环境下的电缆载流量的仿真计算模型，与IEC 60287标准计算结果进行对比，并结合理论分析进行验证。应用该仿真方法研究了邻近效应对直埋电缆载流量的影响，通过改变电缆的排列方式及相间距，指出邻近效应的影响随相间距增大而减小 。

电力电缆；工频磁场；邻近效应；载流量；有限元仿真

随着我国经济实力的迅速提升以及地区用电负荷的飞速增长，高压电力线路已经逐渐深入到人口密集的城镇中心[1]。为节省电力占地走廊和美化城市生活环境，高压电缆线路已逐步代替架空线向负荷中心供电。

电力电缆的敷设一般采用直埋敷设或隧道敷设，对于隧道敷设，可以把它看成在空气中敷设，其载流量主要取决于电缆的最高耐受温度。但对于直埋敷设的电缆来说，由于绝缘热阻大，土壤对电缆散热的影响，再加上绝缘的介质损耗，使同样截面电缆传输容量比隧道敷设线低得多。特别在超高压等级下，介质损耗也占相当大的份额，要传输相同容量，电缆导体截面要比隧道敷设线大得多。尽管国内目前正在积极推广综合管廊建设，但考虑到隧道造价较高，建设速度较慢，目前仍主要采用直埋方式敷设高压电缆。同时，在目前的工程实际中，电缆回路间由工频磁场产生的邻近效应也是不容忽略的[2]。邻近效应改变了电缆金属导体的交流电阻，同时改变了电缆及周围环境的热场分布，造成电缆局部过热，限制了电缆线路的载流量。

载流量的确定是一个比较困难和繁琐的问题，若电缆的载流量偏大，会造成电缆线芯的工作温度超过容许值，绝缘的寿命就会缩短；载流量偏小，则线芯不能得到充分利用，造成不必要的浪费[3]。现有的电缆线路载流量都是依据IEC 60287来确定的，但工程实际运行经验发现，由此计算的载流量与实际运行情况有一定差距[4]。为了提高线路的有效利用率，需要较为准确地给出电缆的长期允许额定载流量。目前，国外已有部分专家运用数值计算法[5-8]研究了邻近效应下的电缆载流量，该方法能更方便地选择计算的边界条件，较好地贴近电缆运行的实际情况。因此，本文采用有限元分析方法仿真计算了直埋电缆的载流量，并应用该方法研究了邻近效应对直埋110 kV交联聚乙烯电缆线路载流量的影响。

1 基本理论

1.1 电磁场基本理论

根据毕奥-沙伐定律，源电流在另一源电流回路的元电流处产生的效应用磁感应强度B来表示，即

(1)

式中：μ0为真空中的磁导率，4π×10-7H·m-1；I′为源电流；dl′为源电流的微小线元素；eR为电流元指向待求场点的单位向量；R为电流两回路相对位置矢量，m。

由式(1)推广，单根流过电流为I的无限长直细导线，周围空间某一点的磁感应强度B的表达式为

(2)

式中：ρ为场点到导线的垂直距离，m；eφ为柱坐标单位向量。

对于多根载流细导线，根据叠加原理，空间一点的磁感应强度可按矢量方法来合成，如图1所示。

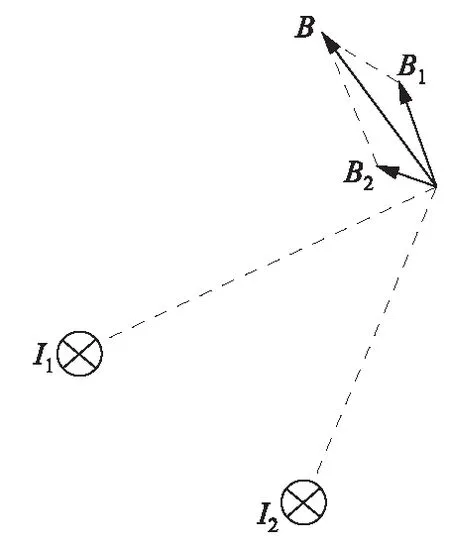
图1 磁感应强度矢量合成

对于单回路三相正弦交流载流细导线的磁场计算，将电流值按相位分为实部和虚部分别进行加载，得到计算点磁感应强度的实部值Br和虚部值Bi，最终磁感应强度计算结果为Bm∠φ，其中Bm和φ的表达式分别为：

(3)

(4)

式中：Bm为单点磁感应强度的幅值，T；φ为单点磁感应强度的相位，(°)。

当导线不能忽略其截面积时，交变的电流流过导线，导线周围变化的磁场也要在其中产生感应电流，从而使沿导线截面的电流分布不均匀。尤其当频率较高时，该电流几乎是在导线表面的一薄层中流动，这就是所谓的集肤效应现象。此外，相互靠近的导体通有交变电流时，每一导体不仅处于自身电流产生的电磁场中，同时还受到其他导体中的电流产生的电磁场的影响。显然，这时各个导体中的电流分布和它单独存在时不同，会受到邻近导体的影响，这种现象称为邻近效应。频率越高，导体靠的越近，邻近效应越显著。

1.2 电缆损耗计算

由于电缆中的热源主要来自导电金属部分的焦耳热损耗，对于单芯电缆来说，主要是线芯和金属护套上的焦耳损耗。载流导体上的电流分布由集肤效应和邻近效应所决定，高压电缆载流量的计算中，电缆线芯及金属护套的发热量与导体的交流电阻有关。交流电阻的表达式为

(5)

式中：R0为导体在允许工作温度下的直流电阻值，Ω；Ys为集肤效应系数；Yp为邻近效应系数。导体直流电阻R0随温度的变化规律为

(6)

式中：R20为导体在20 ℃时的直流电阻，Ω；α20为20 ℃时材料恒定质量温度系数，℃-1；θ为导体最高工作温度，℃。

对于工频为50 Hz的交流电缆，金属护套的厚度和电缆的平均直径相比，可以忽略集肤效应的影响。电缆导体损耗和金属护套损耗可以利用解析的方法，由贝塞尔函数计算[9]。

理想介质电压和电流是正交的，没有损耗，但实际介质存在介质极化电流和电导电流，所以电流和电压夹角小于90°，会产生介质损耗。但根据 IEC 60287标准，对于高联聚乙烯(cross-linked polyethylene,XLPE)无绝缘填充料的电缆，在运行电压低于127 kV时，可以不考虑介质损耗。

1.3 热环境

地下电缆群的稳态温度场属于二维稳态导热问题。热源区域(线芯，金属护套)的温度控制方程为

(7)

式中：T为坐标为(x，y)点的温度，℃；qv为体积发热率，W·m-3。

无热源区域(电缆其他层，土壤)的温度控制方程为

(8)

2 仿真模型

2.1 电缆模型

表1给出了作为研究对象的110 kV XLPE绝缘电缆的结构及参数。

表1 110 kV电缆结构参数和各部分热阻系数

组成层标称厚度/mm内直径/mm外直径/mm热阻系数/(K·m·W-1)导体(铜)--24.01/370.37导体屏蔽层0.924.025.83.5绝缘层(XLPE)18.425.862.63.5绝缘屏蔽层1.062.664.63.5缓冲层4.064.672.66.0金属护套(波纹铝)4.572.681.610.21隔离层0.581.682.66.0衬层1.082.684.66.0外护层(PVC)6.084.696.66.25

注：直埋电缆周围土壤热阻系数为1.0 (m·K)/W。

2.2 温度场建模

电缆群温度场计算的边界条件如图2所示，图中设空气和土壤表面的传热系数为12.5 W/(m2·K)。电缆负载最高时一般为夏季天气最为炎热时期，为考虑极限情况，空气流体温度取40 ℃，深层土壤温度恒为25 ℃。

图2 热分析边界条件

2.3 计算流程

本文采用磁热物理环境顺序耦合的方法来计算电缆载流量。首先，在磁分析物理环境中赋给金属部分一个初始温度25 ℃和一个初始电流载荷，进行有限元工频磁场分析；然后读入热分析物理环境，将电磁分析结果中各部分的损耗值作为热源载荷加载到热分析中，进而求出热分析区域的温度分布结果并找出电缆导体上节点温度的最大值。对交联聚乙烯(XLPE)绝缘电缆，其载流量对应于电缆线芯温度达90 ℃时的稳态工作电流，因此若此温度高于90 ℃，则将初始电流载荷减小，继续磁热耦合分析，反之则将电流载荷增大。计算流程如图3所示。经过反复迭代，直到导体最高温度为90 ℃，允许误差不大于0.1 ℃，此时的电流载荷值即为所求的电缆允许载流量。

图3 磁-热耦合分析流程

3 模型计算结果和IEC标准计算值的比较

针对单回路一字型排列直埋电缆线路，比较按照仿真模型和IEC标准推荐方法分别计算的载流量。

基于热路分析一维算法的IEC 60287载流量计算中的基本假设为：电缆表面及土地表面均为等温面；土地为均匀媒质即热阻系数为常数；热流从电缆散出均向地面流。

本文所采用的磁热耦合载流量计算建模中，土地为均匀媒质即热阻系数为常数，这一点与IEC标准一致，但也存在差异，包括电缆表面和土地表面均不是等温面，热流从电缆散出向地面和周围深层土壤流动，空气和土壤分界面间存在对流换热。采用图4中的单回一字型排列直埋电缆线路模型比较两种方法计算结果。

图4 磁-热耦合一字型排列单回路电缆环境

当金属护套两端牢固接地，相间距s=0.2 m，埋入深度D=1 m，深层土壤温度为25 ℃，土壤表面的传热系数为12.5 W/(m2·K)，空气流体温度为40 ℃时，按照仿真模型计算的载流量为500 A，而根据IEC标准计算时，当土壤温度为25 ℃，相同的敷设条件下，载流量计算值为536.55 A。仿真计算结果为IEC计算值的93.2%。当电缆埋深D=3 m，其他条件不变的情况下，仿真模型计算的载流量为463.22 A，IEC标准计算值为474.8 A。仿真计算结果为IEC标准计算值的97.6%。两种情况下电缆线路上方的土壤表面温度分布如图5所示。

图5 埋深1 m及3 m时土壤表面温度分布

由图5可知，当电缆埋设较深时，土壤表面温差较小，近似为等温面，因此载流量计算值与IEC更为接近。

考虑到电缆埋深一般为1 m左右，且本文考虑为高峰负荷期间的极限条件，因此假设空气流体温度为40 ℃时，使得仿真计算结果比IEC标准计算值小。当假设空气流体温度也为25 ℃，电缆埋深1 m，其他条件不变时，仿真模型计算载流量为563.28 A，比IEC标准的计算结果大了约5.0%。

基于以上算例认为，仿真计算中所建立的环境模型更能反映电缆的实际敷设运行条件。因此，在保证参数设置准确的前提下，可以认为，由本模型及方法计算获得的载流量更能反映电缆的实际负载能力。

4 邻近效应对电缆载流量的影响

由理论分析可知，邻近效应对电缆载流量的影响与回路相间距离有关，除直接改变相间距离外，通过改变排列方式也会间接改变相间距离。

4.1 相间距离对电缆载流量的影响

采用图4中的模型进行计算，维持热场边界条件及埋深D=1 m不变，改变相间距离，直埋敷设单回路一字型排列电缆载流量随电缆相间距的变化规律见表2。

表2 直埋敷设一字型单回线路电缆载流量

相间距/m0.20.30.40.51.0载流量/A500506.25515.63529.69569.53

由表2可知，邻近效应对电缆载流量的影响随电缆相间距离的增大而减小。

4.2 排列方式对电缆载流量的影响

如图6所示，110 kV电缆单回路品字形排列，土壤埋入深度D=1 m。

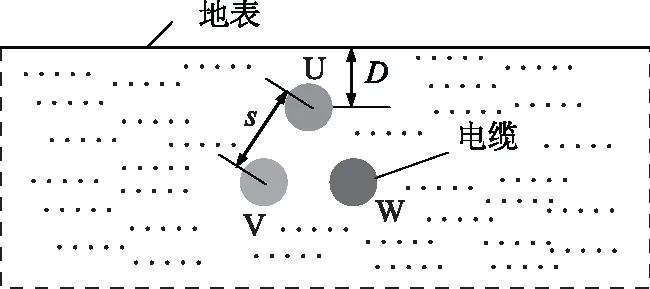
图6 磁-热耦合品字型排列单回路电缆环境示意图

改变相间距离，直埋敷设单回路品字型排列电缆载流量随电缆相间距的变化规律见表3。

表3 直埋敷设品字型单回线路电缆载流量

由表3可知，邻近效应对电缆载流量的影响随电缆相间距离的增大而减小，且品字形排列情况下邻近效应对载流量的影响相对较小，与理论分析结果一致[10-11]。

5 结束语

论文建立了磁-热耦合分析模型，仿真计算了直埋单芯110 kV电缆的载流量，指出该模型较 IEC 60287推荐方法计算结果更为准确。研究了相间距离及排列方式对载流量的影响，对于工程中电缆载流量仿真计算的精度，确定电缆敷设排列方式具有一定意义。

[1] 杨志福.220 kV及110 kV地下电力电缆工频磁场研究[D].北京：华北电力大学，2009.

[2] 马国栋.电线电缆载流量[M].北京：中国电力出版社，2003.

[3] 李熙谋.不同敷设条件下电缆载流量的校正和实用算法[J].电力建设，1997(5)：1-7.

LI Ximou.Calibration and Practical Calculation Method of Cable Ampacity Under the Different Laying Conditions[J].Electric Power Construction, 1997(5)：1-7.

[4] 华良伟.110 kV XLPE电缆载流量计算结果的验证试验[J].电线电缆，2008，5(5)：25-27.

HUA Liangwei.The Verification Test of the Calculated Ampacity of 110 kV XLPE Cables[J].Electric Wire & Cable, 2008,5(5)：25-27.

[5] VAUCHERET P, HARTLEIN R A, BLACK W Z.Ampacity Derating Factors for Cables in Short Segment of Conduit[J].IEEE Transactions on Power Delivery,2005,20(2)：1-6.

[6] MIYAGI D, WAKATSUKI T, TAKAHASHI N.Three-D Finite Element Analysis of Current Distribution in Power Cable Taking Account of E-J Power Law Characteristic[J].IEEE Transactions on Magnetics,2004,40(2)：908-1001.

[7] GEORGE J A.Ration of Electric Power Cables, Ampacity Computation for Transmission, Distribution, and Industrial Application[M].New York：IEEE Press,1997.

[8] 梁永春，柴进爱，李彦明，等.基于FEM的直埋电缆载流量与外部环境关系的计算[J].电工电能新技术，2007，26(4)：10-13.

LIANG Yongchun, CHAI Jinai, LI Yanming, et al.Calculation of Ampacity Reduction Factors for Buried Cables with Surroundings Based on FEM[J].Advanced Technology of Electrical Engineering and Energy, 2007,26(4)：10-13.

[9] FERKAL Kl, POLOJADOFF M, DORISON E.Proximity Effect and Eddy Current Losses in Insulated Cables[J].IEEE Trans.on Power Delivery,1996,11(3)：1171-1178.

[10] 梁永春，柴进爱，李彦明，等.有限元法计算交联电缆涡流损耗[J].高电压技术，2007，33(9)：196-199.

LIANG Yongchun, CHAI Jinai, LI Yanming，et al.Calculation of Eddy Current Losses in XLPE Cables by FEM[J].High Voltage Engineering, 2007, 33(9)：196-199.

[11] 林庆标，牛海清，王晓兵，等.110 kV单芯电缆载流量的研究[C]//中国高等学校电力系统及其自动化专业第二十一届学术年会论文集.南宁：广西大学，2005：638-640.

(编辑 查黎)

Simulation Method for Buried Cable Ampacity and Its Application

LI Wenpei

(Shenzhen Power Supply Co., Ltd., Shenzhen, Guangdong 518001, China)

Recommendation method of IEC 60287 standard is usually used for calculating cable ampacity at present, but in actual engineering practice, the result of this method is different from that of actual situation.Therefore, this paper takes 110XLPE cable under the condition of direct burial installation for a research object and establishes a simulation and calculation model for cable ampacity in magnetic thermal coupling environment.It compares the simulation result with that of IEC 60287 standard and verifies by combining theoretical analysis.It studies influence of proximity effect on ampacity of the buried cable by using this method and points out influence of proximity effect decreases with increase of phase space by research on changing arrangement of cables and phase spaces.

electric power cable; power frequency magnetic field; proximity effect; ampacity; finit

2016-04-24

10.3969/j.issn.1007-290X.2016.11.014

TM726.4

A

1007-290X(2016)11-0070-05

李文沛(1989)，男，山西定襄人。工程师，工学硕士，主要从事电网项目规划设计评审相关工作。