声子聚焦效应对薄膜间接触热阻尺寸效应的影响

陈伟宇 刘晨晗 陶 毅 蔡 爽 魏志勇 毕可东 杨决宽 陈云飞

(东南大学机械工程学院,南京211189)



声子聚焦效应对薄膜间接触热阻尺寸效应的影响

陈伟宇 刘晨晗 陶 毅 蔡 爽 魏志勇 毕可东 杨决宽 陈云飞

(东南大学机械工程学院,南京211189)

采用非平衡态分子动力学方法,模拟计算了多层石墨烯之间和硅薄膜之间的接触热导随薄膜厚度增长的变化趋势.模拟结果显示,多层石墨烯之间的接触热导在厚度方向有显著的尺寸效应,随着厚度的增大,接触热导显著增大,而硅薄膜之间的接触热导随着厚度的增大没有明显变化.另外,根据声子辐射理论,采用各向异性的Debye模型,定义了接触热导尺寸效应强度α,并计算了尺寸效应强度随薄膜厚度增长的变化趋势.结果显示,声子聚焦效应对薄膜间接触热导的尺寸效应有很大影响.该结论有助于建立薄膜之间的接触热导模型和调控纳米复合材料的传热学性质.

分子动力学;声子聚焦;声子辐射;接触热导;尺寸效应

对于非金属和大部分半导体,声子是其主要能量载流子.当纳米材料的几何尺寸小于其体态平均自由程时,声子在边界的散射会大大影响声子传输效率[1-3].Li等[1]测得硅纳米线的热导率在常温下可比体态硅小2个数量级,且有明显的尺寸效应.Chen等[2]研究发现,声子在粗糙表面会加强散射,进一步减小纳米线的热导率.这说明在光滑硅纳米线中有部分声子在边界发生了镜面反射[4].当边界变得粗糙时,这部分声子也发生散射,从而进一步降低硅纳米线热导率.类似地,当薄膜厚度小于其对应的体态平均自由程时,热导率会小于其体态值[3].当2层薄膜有重叠时,薄膜之间会形成界面,当声子打到这些界面时,界面两侧材料的性质和界面处的结合强度决定了声子透过界面的概率[5].但是,由于纳米材料的边界会反射部分声子,原本透过界面的声子可能又会回到入射一侧,使得实际透过界面的声子减少,即纳米材料之间的界面热导也可能存在尺寸效应[6-7].

在体态情况下,界面热导和界面两侧材料的尺寸是无关的[8].而当界面两侧的材料尺寸为纳米量级时,界面热导与界面两侧材料的尺寸是相关的.Liang等[7, 9]采用分子动力学方法模拟了纳米薄膜与体态基底之间界面热导的尺寸效应,并以声学失配模型[10]为框架,通过考虑声子的多次反射和透射,给出了声子的有效透射率与薄膜厚度的关系.当把上述的体态基底换成同种材料的纳米薄膜时,声子的反射和透射变得更加复杂,难以直接给出声子的有效透射率.Yang等[11]测得了交叉多壁碳纳米管之间的接触热导,发现随着多壁碳纳米管层数的增加接触热导增大,证实了接触热导的尺寸效应.通过类比多层石墨烯层与层之间的界面热导,他们把这一现象归因于声子在界面处的多次反射和石墨法向较长的声子平均自由程,同时运用简化的蒙特卡罗法,分析了各向异性材料的声子聚焦效应对界面热导尺寸效应的影响,但并未直接给出各向同性材料薄膜之间的界面热导随薄膜厚度变化的趋势.

本文运用分子动力学方法,模拟了多层石墨烯之间以及硅薄膜之间的接触热阻与薄膜厚度的关系,比较了材料的各向异性和各向同性对接触热阻尺寸效应的影响,并通过定义计算接触热导尺寸效应强度,进一步阐明了声子聚焦效应对薄膜之间接触热导尺寸效应的影响.

1 分子动力学模型

图1(a)为分子动力学模型示意图.模型中,上下两层相同的薄膜平行堆叠,在中间连接的窗口部分为接触面,窗口宽度为2.53 nm.在x和y方向施加周期性边界条件,在z方向施加自由边界条件,这样可使接触部分上下薄膜的距离能够自由调节达到平衡,且不会引入内应力.对多层石墨烯,同层碳原子之间的碳-碳共价键通过Tersoff作用势[12]来描述,不同层碳原子之间的非共价键采用vdW(van der Waals)作用势:

(1)

式中,V(r)为势能;ε为势阱常数;σ为平衡常数;r为原子之间的距离.对于硅薄膜,薄膜内的硅-硅共价键采用SW(Stillinger-Weber)作用势[13].对于上下两层薄膜的接触部分,均采用vdW作用,参数见表1.分子动力学模拟过程采用LAMMPS[14]软件包实现,模拟时间步长为0.5 fs.

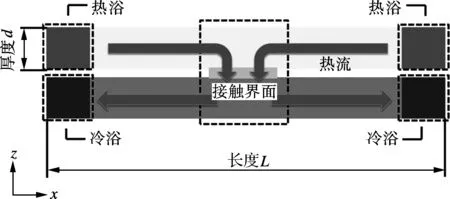
(a) 分子动力学模型示意图

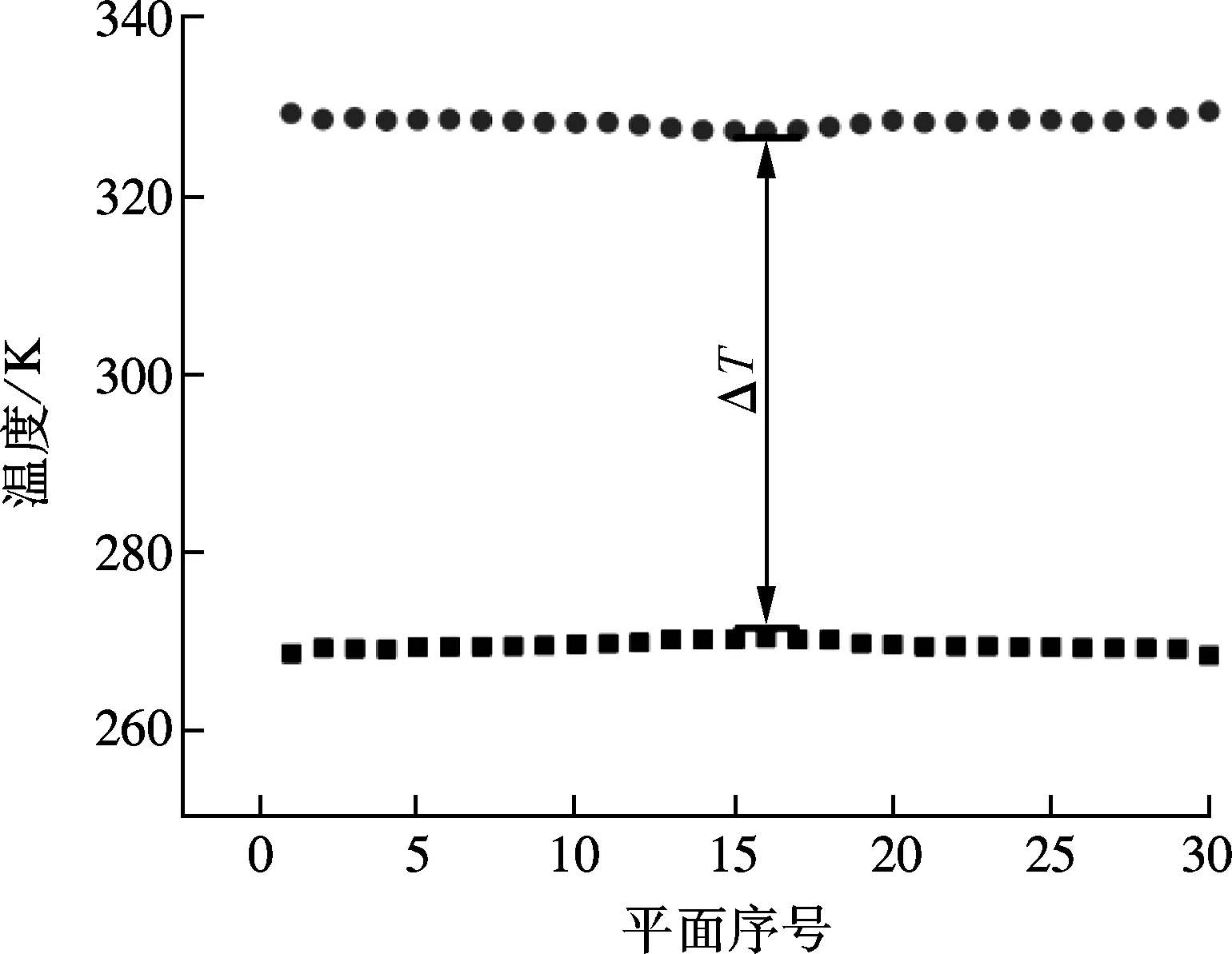
(b) 沿着x方向的温度分布图

薄膜类型ε/meVσ/nm多层石墨烯[11]3．000．340硅薄膜[15]13．440．384

在模拟过程中,先采用NPT系综把系统温度调至300 K,待平衡后,计算出薄膜的晶格常数,利用所得到的晶格常数来排列薄膜的每个原子.然后利用NVT系综把温度重新调回300 K,待系统稳定后使用NVE系综,检查温度是否稳定在300 K.如果温度稳定,说明系统已在能量最小点,开始施加热流.施加热流一般有2种方法:固定温度差[16]和固定热流[17].本文通过在上层薄膜两端添加能量,下层薄膜减去相同能量的方法,在保证系统能量守恒的前提下,形成图1(a)中所示的热流.施加热流过程中,对上下薄膜沿着x方向分别划分等间隔的小区间,监测每个小区间温度的变化.当每一层区间的温度达到平衡时,认为系统达到稳态.然后模拟足够多的步数,对每个小区间的瞬时温度取平均值,得到薄膜的温度分布,如图1(b)所示.模拟结果显示,施加热流5 ns后,系统达到稳态.在系统达到稳态后的5 ns内,对每个小区间的温度取平均值得到薄膜的温度分布.上下两层薄膜之间接触处的界面热导可根据下式计算:

(2)

式中,GCA为接触热导;ΔE为单位时间内上下层薄膜两端添加或减去的能量;A为接触面积;ΔT为上下层薄膜接触处的温度差.

2 模拟结果与分析

多层石墨烯薄膜之间接触热导的模拟模型如图2(a)所示,单层碳原子的晶格为正六边形结构,层与层之间按照A-B模式堆叠.本文模拟了不同长度和层数的多层石墨烯间的接触热导,模拟结果如图2(b)所示.在相同长度下,随着层数从1层增加到8层,热导显著增大.对特定层数的多层石墨烯,随着薄膜长度L从15 nm增长到120 nm,热导开始迅速增大,随后趋于平缓.这是由于模拟中的热阻包含两部分:① 上下薄膜之间的接触热阻;② 施加热流引起的热阻.前者贡献的热导和薄膜长度无关,而后者贡献的热导与薄膜长度成正比.在施加热流时,热浴中激发出大量高频声子,这些声子为了通过接触界面,必须先转化为低频声子.在这个过程中产生的热阻可以通过倒数拟合[18]来剔除.图2(c)是通过倒数拟合后得到的热导与石墨烯层数D的关系,模拟结果显示热导随着石墨烯层数的增大而明显增大.

(a) 石墨烯薄膜之间接触热导的模拟模型

(b) 接触热导与石墨烯薄膜长度的关系

(c) 接触热导与石墨烯薄膜层数的关系

硅纳米薄膜之间接触热导的模拟模型如图3(a)所示,硅薄膜的x方向为[1 0 0]方向,晶胞为金刚石结构.与多层石墨烯不同,长度对硅薄膜之间接触热导的影响基本可忽略不计.例如,厚度(d)为2.2 nm的薄膜,当其长度从17 nm增长到140 nm,硅薄膜之间的接触热导在45 MW/(m2·K)上下波动.这是由于硅是各向同性材料,施加热流时,热浴中被人为激发出的高频声子可以向各个方向传输并转化为能够通过接触界面的低频声子.而多层石墨烯中,声子的聚焦效应[19]使得声子分别朝面向和法向聚焦,面向和法向声子之间的耦合减弱,使得声子只能沿着面向传输并转化为能够通过界面的低频声子,导致热导在长度方向有明显的尺寸效应.图3(b)显示,对长度分别为17.4 nm和34.8 nm的硅薄膜,当其厚度从1 nm增加到17 nm时,热导没有明显变化.

(a) 硅薄膜之间接触热导的模拟模型

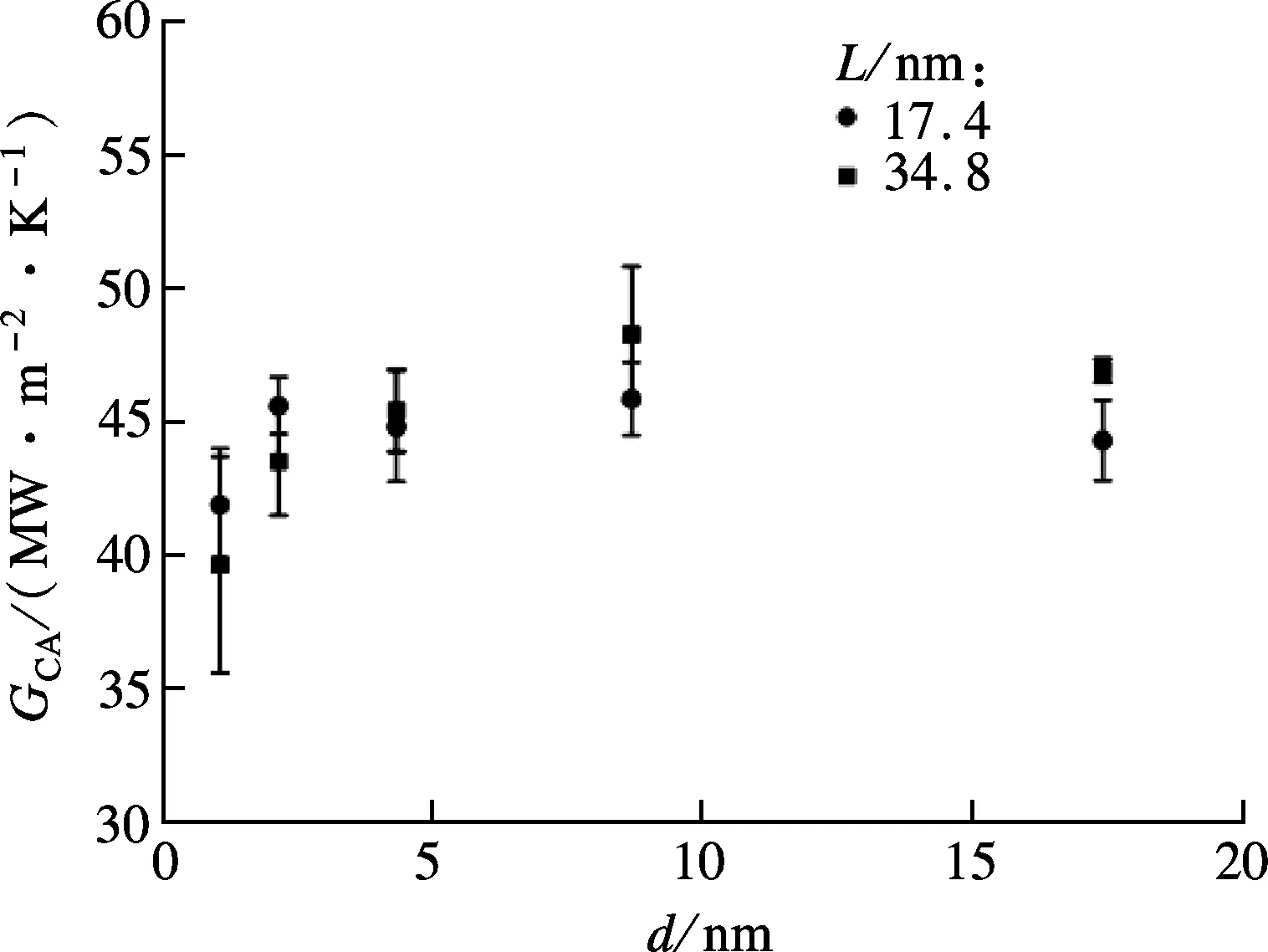
(b) 硅薄膜之间接触热导与薄膜厚度的关系

为了更好地比较材料的各向异性对接触热导的影响,本文将多层石墨烯之间的接触热导按照单层石墨烯间的热导进行归一化,单层石墨烯厚度选取为0.34 nm,而硅薄膜之间的接触热导按照厚度为1.1 nm硅薄膜的热导进行归一化,结果如图4所示.本文模拟得到的石墨烯热导随着薄膜厚度的增加而显著增大,与Yang等[11]的模拟结果一致.与之相反,硅薄膜之间的热导随着厚度增加几乎不变.在多层石墨烯薄膜之间和硅薄膜之间,接触处均采用vdW作用,这与单层石墨烯层与层之间的作用形式相同,但是与硅薄膜中的作用形式不同.为了排除接触力形式对结果的影响,本文还模拟了SW接触形式下硅薄膜之间的接触热导.在SW接触形式下,为了使薄膜之间出现温降,所模拟的薄膜厚度必须大于窗口宽度,否则,在热流方向上接触处的热阻将占总热阻的比例很小,从而难以统计接触面两端的温度差.模拟结果显示,接触力形式的变化并没有改变热导随厚度增大的变化趋势.综上所述,材料的各向异性增强了薄膜之间接触热导与薄膜厚度相关的尺寸效应.

图4 归一化接触热导与薄膜厚度的关系

为了进一步解释各向异性材料的声子聚焦效应对薄膜之间接触热导尺寸效应的影响,本文采用各向异性的Debye模型[19],通过计算声子辐射[19-21]来衡量对接触热导有尺寸效应贡献的声子在所有对接触热导有贡献的声子中所占的比例.根据热辐射理论,界面接触热导可由下式计算:

(3)

式中,q为热流密度;H为声子辐射功率;T为温度;t为声子透过界面的平均概率.根据热导随温度的变化趋势,在室温下,近似认为t是与温度无关量.若采用经典的声子分布,界面接触热导可由下式表示:

(4)

(5)

(6)

式中,ka,m,kb,m,kc,m为布里渊区边界;N为离散点数目；ρ,θ,φ为球坐标的坐标变量,ρ∈[0,1],θ∈[0,π],φ∈[0,2π].

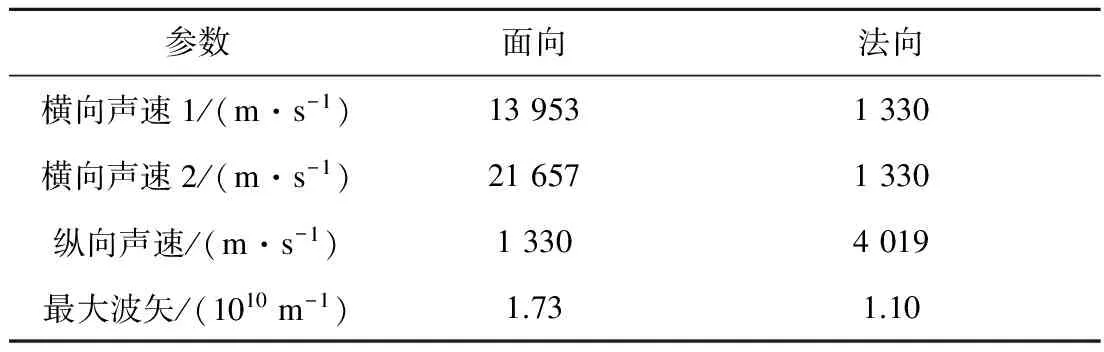
表2 石墨的Debye模型参数[22-23]

表3 体态硅的Debye模型参数[24]

假设声子从接触窗口的中心出发,从热浴端入射到冷浴端,如果声子从发射到最终散射,有且只有一次通过界面,则这部分声子对接触热导的尺寸效应没有贡献,反之则有贡献.同时假设所有的声子在经过其平均自由程l后发生散射.则可定义接触热导尺寸效应强率为

(7)

式中,Nα为满足上述假设的离散采样点数目；ρ,θ,φ的取值满足上述假设.α也可表示对接触热导有尺寸效应贡献的声子在所有对接触热导有贡献的声子中所占的比例.本文取石墨法向的平均自由程为135.3 nm[11, 25],硅的平均自由程为54.65 nm[3],则α随薄膜厚度增大的变化趋势如图5所示.由图可见,随着薄膜厚度的增大,接触热导的尺寸效应强度逐渐减小,多层石墨烯间接触热导的尺寸效应强度始终大于硅薄膜的尺寸效应强度.图5中多层石墨烯对应的曲线在厚度为2 nm附近有一个突变,且在这之前始终保持很强的尺寸效应.这是因为多层石墨烯的声子聚焦效应使得相关声子的群速度方向都聚焦在法向方向,在薄膜厚度较薄时,声子在传播时偏离法向的距离很小,声子基本上都能返回到界面的入射端,满足上述发生尺寸效应的假设条件.当厚度增大到一定程度时,声子偏离法向的距离增大,反射时被接触面以外的界面阻止回到入射端,成为对接触热导没有尺寸效应贡献的声子.对硅薄膜而言,接触热导在厚度小于5 nm时有较强的尺寸效应,这与分子动力学结果不太吻合.这是由于在分子动力学模拟中,硅薄膜的边界原子会发生重构,声子到达界面时会部分散射,从而减弱了接触热导的尺寸效应.

图5 接触热导尺寸效应强度与薄膜厚度的关系

3 结语

本文采用非平衡态分子动力学方法,模拟计算了多层石墨烯之间和硅薄膜之间的接触热导随薄膜厚度增长的变化趋势,以比较材料的各向异性对接触热导尺寸效应的影响.根据声子辐射理论,应用各向异性的Debye模型,定义了尺寸效应强度,并计算了各向异性强度随薄膜厚度增长的变化趋势,结果显示各向异性材料的声子聚焦效应对薄膜间接触热导的尺寸效应有很大贡献.本文结果对后续建立薄膜之间的接触热导模型有重要意义,同时也为纳米复合材料传热学性质的调控提供了理论依据.

References)

[1]Li D Y, Wu Y Y, Kim P, et al.Thermal conductivity of individual silicon nanowires[J].AppliedPhysicsLetters, 2003, 83(14): 2934-2936. DOI:10.1063/1.1616981.

[2]Chen R, Hochbaum A I, Murphy P, et al.Thermal conductance of thin silicon nanowires[J].PhysicalReviewLetters, 2008, 101(10): 105501. DOI:10.1103/PhysRevLett.101.105501.

[3]Marconnet A M, Asheghi M,Goodson K E. From the Casimir limit to phononic crystals: 20 years of phonon transport studies using silicon-on-insulator technology[J].JournalofHeatTransfer, 2013, 135(6): 061601. DOI:10.1115/1.4023577.

[4]Xie G, Guo Y, Li B, et al.Phonon surface scattering controlled length dependence of thermal conductivity of silicon nanowires[J].PhysicalChemistryChemicalPhysics, 2013, 15(35): 14647-14652. DOI:10.1039/c3cp50969a.

[5]Prasher R. Acoustic mismatch model for thermal contact resistance of Van Der Waals contacts[J].AppliedPhysicsLetters, 2009, 94(4): 041905. DOI:10.1063/1.3075065.

[6]Li D, McGaughey A J H. Phonon dynamics at surfaces and interfaces and its implications in energy transport in nanostructured materials-An opinion paper[J].NanoscaleandMicroscaleThermophysicalEngineering, 2015, 19(2): 166-182. DOI:10.1080/15567265.2015.1035199.

[7]Liang Z, Sasikumar K,Keblinski P. Thermal transport across a substrate-thin-film interface: Effects of film thickness and surface roughness[J].PhysicalReviewLetters, 2014, 113(6): 065901. DOI:10.1103/PhysRevLett.113.065901.

[8]Krenzer B, Hanisch-Blicharski A, Schneider P, et al.Phonon confinement effects in ultrathin epitaxial bismuth films on silicon studied by time-resolved electron diffraction[J].PhysicalReviewB, 2009, 80(2):024307. DOI:10.1103/physrevb.80.024307.

[9]Liang Z, Keblinski P. Finite-size effects on molecular dynamics interfacial thermal-resistance predictions[J].PhysicalReviewB, 2014, 90(7): 075411. DOI:10.1103/physrevb.90.075411.

[10]Swartz E T, Pohl R O. Thermal boundary resistance[J].ReviewsofModernPhysics, 1989, 61(3): 605-668. DOI:10.1103/revmodphys.61.605.

[11]Yang J K, Shen M, Yang Y, et al.Phonon transport through point contacts between graphitic nanomaterials[J].PhysicalReviewLetters, 2014, 112(20): 205901. DOI:10.1103/physrevlett.112.205901.

[12]Tersoff J. Empirical interatomic potential for carbon, with applications to amorphous-carbon[J].PhysicalReviewLetters, 1988, 61(25): 2879-2882. DOI:10.1103/PhysRevLett.61.2879.

[13]Stillinger F H, Weber T A. Computer simulation of local order in condensed phases of silicon[J].PhysicalReviewB, 1985, 31(8): 5262-5271. DOI:10.1103/physrevb.31.5262.

[14]Plimpton S. Fast parallel algorithms for short-range molecular dynamics[J].JournalofComputationalPhysics, 1995, 117(1): 1-19. DOI:10.1006/jcph.1995.1039.

[15]Mayo S L, Olafson B D,Goddard W A. Dreiding: A generic force field for molecular simulations[J].TheJournalofPhysicalChemistry, 1990, 94(26): 8897-8909. DOI:10.1021/j100389a010.

[16]Maiti A, Mahan G D,Pantelides S T. Dynamical simulations of nonequilibrium processes—heat flow and the kapitza resistance across grain boundaries[J].SolidStateCommunications, 1997, 102(7): 517-521. DOI:10.1016/s0038-1098(97)00049-5.

[17]Jund P, Jullien R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica[J].PhysicalReviewB, 1999, 59(21): 13707-13711. DOI:10.1103/physrevb.59.13707.

[18]Huxtable S T, Cahill D G, Shenogin S, et al.Relaxation of vibrational energy in fullerene suspensions[J].ChemicalPhysicsLetters, 2005, 407(1/2/3): 129-134. DOI:10.1016/j.cplett.2005.03.052.

[19]Chen Z, Wei Z, Chen Y, et al.Anisotropic Debye model for the thermal boundary conductance[J].PhysicalReviewB, 2013, 87(12): 125426. DOI:10.1103/physrevb.87.125426.

[20]Dames C, Chen G. Theoretical phonon thermal conductivity of Si/Ge superlattice nanowires[J].JournalofAppliedPhysics, 2004, 95(2): 682-693.

[21]Wei Z, Chen Y,Dames C. Negative correlation between in-plane bonding strength and cross-plane thermal conductivity in a model layered material[J].AppliedPhysicsLetters, 2013, 102(1): 011901. DOI:10.1063/1.4773372.

[22]Blakslee O L, Proctor D G, Seldin E J, et al.Elastic constants of compression-annealed pyrolytic graphite[J].JournalofAppliedPhysics, 1970, 41(8): 3373-3382. DOI:10.1063/1.1659428.

[23]Kelly B T, Walker P L Jr. Theory of thermal expansion of a graphite crystal in the semi-continuum model[J].Carbon, 1970, 8(2): 211-226. DOI:10.1016/0008-6223(70)90116-8.

[24]Chen W, Yang J, Wei Z, et al.Effects of interfacial roughness on phonon transport in bilayer silicon thin films[J].PhysicalReviewB, 2015, 92(13): 134113. DOI:10.1103/physrevb.92.134113.

[25]Wei Z, Yang J, Chen W, et al.Phonon mean free path of graphite along the c-axis[J].AppliedPhysicsLetters, 2014, 104(8): 081903. DOI:10.1063/1.4866416.

Effect of phonon focusing on thickness-dependent contact thermal conductance between thin films

Chen Weiyu Liu Chenhan Tao Yi Cai Shuang Wei Zhiyong Bi Kedong Yang Juekuan Chen Yunfei

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

Thickness-dependent contact thermal conductance(CTC) between multilayer graphene as well as silicon thin films was investigated using the nonequilibrium molecular dynamics simulation method. The simulation results show that the CTC between multilayer graphenes is thickness dependent, and increases as the thickness gets larger. However, the CTC between silicon thin films is almost thickness independent. In addition, according to the phonon irradiation theory and the anisotropic Debye model, size effect strengthαwas defined and was calculated to show its variation trend as the film thickness increases. The results show that the phonon focusing dose plays an important role in the thickness dependence of CTC. This conclusion is helpful in establishing the model of CTC between thin films and in controlling the engineering thermal transport properties of nanocomposites.

molecular dynamics; phonon focusing; phonon irradiation; contact thermal conductance; size effect

10.3969/j.issn.1001-0505.2016.06.008

2016-02-29. 作者简介: 陈伟宇(1987—)，男，博士生；陈云飞(联系人)，男，博士，教授，博士生导师，yunfeichen@seu.edu.cn.

国家自然科学基金重点资助项目(51435003)、江苏省普通高校学术学位研究生创新计划资助项目(KYLX15_0058)、东南大学优秀博士学位论文培育基金资助项目(YBJJ1541).

陈伟宇，刘晨晗,陶毅,等.声子聚焦效应对薄膜间接触热阻尺寸效应的影响[J].东南大学学报(自然科学版),2016,46(6):1155-1160.

10.3969/j.issn.1001-0505.2016.06.008.

O469

A

1001-0505(2016)06-1155-06