基于LMI的4WS-4WD车辆H∞鲁棒控制器设计

殷国栋 吴 昊 张 宁 陈建松

(东南大学机械工程学院, 南京 211189)



基于LMI的4WS-4WD车辆H∞鲁棒控制器设计

殷国栋 吴 昊 张 宁 陈建松

(东南大学机械工程学院, 南京 211189)

基于线性矩阵不等式(LMI)设计了H∞鲁棒最优控制器以及H∞鲁棒非脆弱控制器.通过两自由度(2-DOF)车辆模型推导并建立H∞鲁棒控制系统,此外,定义系统摄动并对摄动矩阵进行分解,进而利用线性矩阵不等式求解控制器.仿真结果表明,H∞鲁棒最优控制器对侧偏角及横摆角速度的控制效果显著优于LQR控制器.同时,在控制器存在摄动及对侧偏角及横摆角速度进行控制的情况下,H∞鲁棒非脆弱控制器的鲁棒性能显著优于普通鲁棒H∞控制器.因此,H∞鲁棒最优控制器解决了普通鲁棒H∞控制器控制性能差的问题,H∞鲁棒非脆弱控制器则解决了普通H∞鲁棒控制器对参数变化敏感的问题.

H∞鲁棒控制;LMI;车辆动力学;最优控制;非脆弱控制

近年来,各国政府及各大汽车制造商对电动汽车研究均投入巨大精力.伴随着电动汽车各项主动安全技术、被动安全技术的成熟与应用,未来的电动汽车将具有十分复杂的汽车电子系统.车辆电子系统中既有主控制器,又同时存在转向控制器、电机控制器等各种辅助驾驶设备控制器.这在减轻驾驶人员负担的同时也带来了车辆系统参数波动的问题以及更加复杂的控制器参数摄动问题.这种情况下,最优控制的控制效果变差.同时,普通的鲁棒H∞控制器的控制功能实现还取决于控制器的精确控制,但鲁棒控制器设计方法对控制器参数变化极其敏感,这种控制器被称为脆弱控制器.因此,近几年非脆弱控制器成为研究热点之一.本文建立了基于车辆系统设计的H∞鲁棒控制系统,通过线性矩阵不等式(linear matrix inequalities,LMI)设计了H∞鲁棒最优控制器及H∞鲁棒非脆弱控制器.H∞鲁棒最优控制器可以兼顾控制性能及鲁棒性能.H∞鲁棒非脆弱控制器可以抑制控制器参数的波动.

1 国内外研究现状

模糊逻辑控制在四轮转向(four wheel steering,4WS)及四轮独立驱动控制(four wheel driving,4WD)领域得到众多研究人员的关注.Ozatay等[1]在车辆控制系统中采用模糊控制算法以及最小侧偏角误差算法,结果表明模糊逻辑控制的车辆可以在短暂的运动中提供零侧偏角,并保证横摆角速度的快速响应.Aslam等[2]设计了模糊滑模控制算法,该算法应用在车辆高速过弯时,通过动态反馈控制器抵消轮胎与地面相互作用力的影响,消除传统滑模控制中遇到的抖振现象.Fahimi[3]采用后轮转角整合模糊控制策略以及横摆力矩控制策略,使4WS-4WD车辆获得优异的侧偏角以及横摆角速度性能,数值模拟结果表明后轮整合模糊控制策略可以有效地避免车辆转向过程中的不稳定.胡国强[4]为了分析轮胎的侧偏特性等非线性因素,引入了模糊控制,设计了基于横摆角速度的反馈控制系统,并将其与其他控制方法进行比较,验证了模糊控制可应用于非线性四轮转向车辆中.Yin等[5]提出了4WS车辆的μ综合控制,以横摆角速度跟踪反馈为控制逻辑,设计μ综合鲁棒控制器来抑制外部干扰,实现了传统四轮转向车辆控制器难以达到的鲁棒性能.Kolodziej[6]提出了自适应控制方法,采用自适应极点配置算法以及最小二乘法使车辆在不安全条件下,采用后轮辅助转向达到车辆稳定的目标.

另一方面,H∞鲁棒控制器得到各领域研究人员的关注.Du等[7]研究了主动车辆悬架的H∞鲁棒非脆弱控制器,结果证明,控制器参数变化时,系统也可以保持闭环稳定并获得最优性能.Gao等[8]设计了航天器交会系统H∞鲁棒非脆弱控制器,该控制器能保证航天器在交会过程中,即使交会系统参数存在不确定性、输入受约束和外部控制器存在扰动,也能够顺利完成交会任务.Kchaou等[9]提出了一种基于时间混沌系统的H∞观测器的非脆弱控制器设计方法.Liu等[10]研究了不确定线性中立与时变延迟系统的控制问题,其中延迟包括快速变化的情况.Xu等[11]研究了非脆弱H2和H∞滤波器设计问题中的二维离散系统,该系统采用具有多面体不确定性的Roesser模型.

2 基于车辆模型的H∞标准系统

2.1 三自由度实车模型

为了得到控制系统中所需要的实际车辆参数,本文采用三自由度(three degrees of freedom,3-DOF)车辆模型来计算实际车辆的运行参数,模型参数包括4个车轮转角,体现四轮电动汽车的特性.参数还包括4个车轮输出转矩,表示电动汽车ECU控制的电机输出转矩.图1为车辆的俯视图和后视图.图中,δf1,δf2为左、右前轮的转角;δr1,δr2为左、右后轮的转角;T1,T2为左、右前轮的电机转矩;T3,T4为左、右后轮的电机转矩;vx,vy为车辆的纵向和横向速度;β为侧偏角;r为横摆角速度;dt为车辆的一半宽度,df为车辆质心到前轴的垂直距离，dr为车辆质心到后轴的垂直距离;x轴为车身纵轴，y为车身横轴;Φ为车身侧倾角;p为侧倾角速度;ms为簧上质量;KΦ,CΦ为悬架的等效刚度和等效阻尼;hs为簧上质量质心到侧倾轴的距离;z轴为与地面垂直的坐标轴.

(a) 俯视图

(b) 后视图

通过动力学方程得到如下3个方程:

(1)

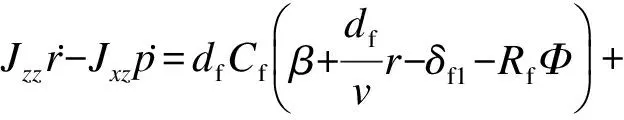
(2)

(3)

式中,mu为车辆总质量;Cf,Cr分别为前轮和后轮侧偏刚度;Rf,Rr分别为前轮和后轮侧倾系数;Rt为车轮半径;Jzz,Jxx分别为簧上质量沿z轴和x轴的转动惯量性;Jxz为簧上质量沿x,z轴的质量惯性积;CΦ为悬架的等效阻尼.

将式(1)～(3)转化为状态空间的形式,即

(4)

x={β,r,p,Φ}T

(5)

u={δf1,δf2,δr1,δr2,T1,T2,T3,T4}T

(6)

(7)

(8)

(9)

2.2 两自由度理想模型和误差模型

本文采用理想模型来建立闭环系统,并用于计算侧偏角、横摆角速度实际值与理想值的误差.因此,理想模型对于控制器设计至关重要,决定着控制器的控制效果.

本文采用两自由度(twodegreesoffreedom,2-DOF)车辆模型推导理想侧偏角及横摆角速度.两自由度模型忽略了侧倾运动,只考虑横向运动和横摆运动.前轮转向角为系统的输入,假设2个前轮转角相同,即左前轮转角等于前轮右转角,后轮转角为零,轮胎模型为线性模型,则动力学方程为

(10)

(11)

式中,δ为系统输入前轮转角;M为附加力矩.得到理想模型后可以发现,车辆的理想侧偏角及横摆角速度由输入转向角来决定,其状态空间方程为

(12)

(13)

(14)

(15)

(16)

在理想情况下,车辆运行过程中附加力矩不起作用,故在推导时暂时不考虑附加力矩M,即

(17)

根据式(17),关于系统输入转向角δ的侧偏角和横摆角速度的传递函数可以改写为

当s=0,侧偏角和横摆角速度的稳态响应为

(20)

(21)

式(18)和(19)皆为二阶传递函数,作为理想传递函数过于复杂,故将其简化为一阶传递函数.根据祁永宁等[12]提出的简化方法,可以得到

(22)

(23)

(24)

(25)

同时,定义误差模型为理想模型和实际模型的侧偏角误差Δβ以及横摆角速度误差Δr,即

(26)

结合考虑附加力矩,式(26)可以写成状态空间的形式,即

(27)

(28)

2.3 H∞鲁棒控制系统

H∞控制是一种鲁棒控制方法,标准H∞控制结构如图2所示,图中,w为参考输入,或者外部干扰输入;P(s)为一个增广系统;z为被控输出;K为控制器.

图2 标准H∞控制问题

结合车辆误差模型,w可以看作是车辆的输入转角,被控输出为加权运算后的侧偏角实际值与理想值的误差以及横摆角速度实际值与理想值误差,控制器输入为侧偏角、横摆角速度实际值与理想值的误差,控制器输出为车辆附加力矩M.由此得到如下方程:

(29)

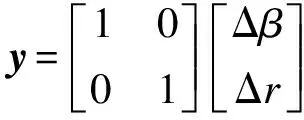
(30)

(31)

式中,Wβ,Wr分别为Δβ及Δr的加权参数.

2.4 车辆控制策略

四轮转向策略采用前馈加反馈的控制策略,后轮转角根据前轮转角、车速及横摆角速度来计算,车辆整体的控制结构如图3所示.

图3 整车控制模型

假设左前轮转角等于右前轮转角,左后轮转角等于右后轮转角,即

δf1=δf2,δr1=δr2

(32)

δr=C1δf+C2r

(33)

(34)

在式(33)中,根据Fukui等[13]提出的理论,C1=-1,C2由式(34)决定,C2的数值与车辆状态量有关.输出的横摆角速度r作为后轮转向系统的反馈信号,从而可以计算得到后轮转向角度.

3 H∞鲁棒最优控制器设计

3.1 H∞鲁棒最优控制器设计理论

(35)

ΔA(t)=M1F(t)N1FT(t)F(t)≤I, ∀t

(36)

根据Li等[14]提出的分解方法,ΔA(t)可以分解如下:

F(t)= diag(Σ11,Σ12,…,Σ1n,Σ21,Σ22,…,

Σ2n,…,Σn1,Σn2,…,Σnn)

(37)

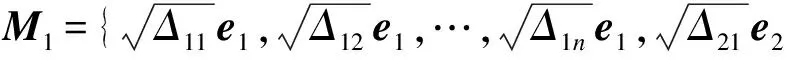
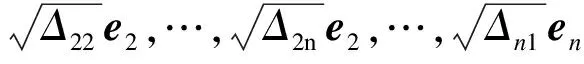
(38)

(39)

系统1可以改写为

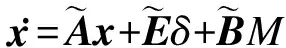
(40)

(41)

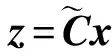
(42)

对于系统1,采用状态反馈控制律设计控制器, 根据鲁棒控制应用理论,可以得到计算鲁棒最优控制器的线性矩阵不等式(LMI),即

(43)

(44)

当式(43)有解时,可求解得到控制器,即

Kzy=YX-1

(45)

本文选取ε1=1,γ=4,Q={100,1},R=1.本文中理想侧偏角为零,前期工作所设计的控制器能很好地跟踪横摆角速度,但跟踪侧偏角效果很差,所以权重函数选择时,加大侧偏角的比重,减小横摆角速度比重,以平衡2个参数的跟踪性能.设定侧偏角与横摆角速度的权重比例为100∶1,同时,因为控制策略不考虑车辆燃油经济性,因此控制变量u,即附加力矩M的权重R也设定为1.根据上述考虑,确定了控制器相关参数.此时,得到非脆弱控制器Kzy为

(46)

3.2 H∞鲁棒最优控制器的数值模拟

仿真参数如表1所示,参数为文献[15]进行车辆仿真实验时采用的参数.

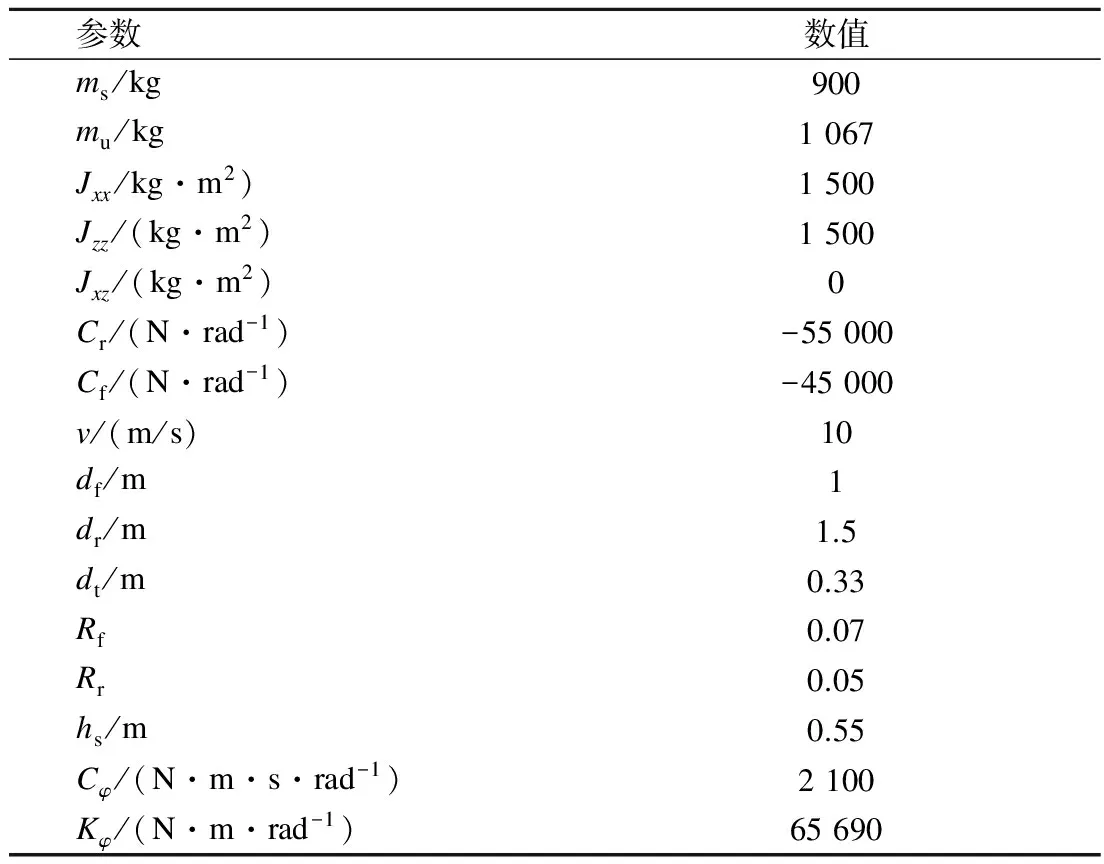
表1 车辆仿真参数

获得控制器后,建立了整车闭环系统,设定系统输入为车辆前轮转角,输入信号在第1 s时信号从0变化至0.05 rad,即大约2.5°,作为角阶跃输入信号.观察质心侧偏角和横摆角速度,评价控制策略对车辆操纵稳定性的影响.

图4是使用LQR控制器及最优控制器在系统摄动下的侧偏角响应.由图可以看出,鲁棒最优控制器的控制性能比LQR控制器要好,鲁棒最优控制器侧偏角比LQR控制器的小0.03 rad左右.鲁棒最优控制器在系统参数有摄动的情况下,其输出值保持稳定,LQR控制器则有明显波动.图4中数据显示,在侧偏角响应方面,鲁棒最优控制器与LQR控制器相比,既有优异的控制性能,又有优异的鲁棒性能.

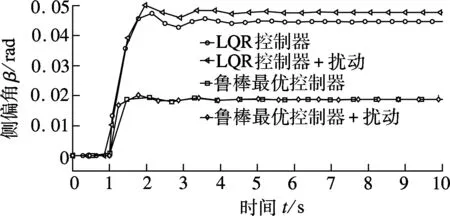
图4 LQR控制器与鲁棒最优控制器的侧偏角响应

图5是使用LQR控制器及鲁棒最优控制器在系统摄动下的横摆角速度响应.从图中可以看到,鲁棒最优控制器的控制性能比LQR控制器要优异很多,鲁棒最优控制器的横摆角速度响应基本稳定在0.2 rad/s,而LQR控制器的横摆角速度达到了0.7 rad/s左右,已经处于危险状态,给车辆带来行驶风险.鲁棒最优控制器在系统参数有摄动的情况下,其输出值也可以保持稳定,LQR控制器则不能保持稳定.总之,在横摆角速度响应方面,鲁棒最优控制器既有良好的控制性能,也有优异的鲁棒性能.

图5 LQR控制器与鲁棒最优控制器的横摆角速度响应

4 H∞鲁棒非脆弱控制器设计

4.1 H∞鲁棒非脆弱控制器设计理论

非脆弱控制器中非脆弱的含义主要是指控制器对参数扰动有抑制作用.因此,非脆弱控制器在设计时就需要同时考虑系统的不确定性以及控制器的不确定性.

根据Sun[16]提出的理论,考虑控制器的摄动是加法式摄动,系统中的控制器摄动表示如下:

(47)

根据不确定系统得到H∞鲁棒非脆弱控制器控制律,如果对于给定的ε1>0,ε2>0,γ>0,系统1在状态反馈H∞鲁棒非脆弱控制器下是二次稳定的,并且z(t)满足H∞性能指标约束.此时,若存在对称矩阵X>0,Y>0,则下面的线性矩阵不等式成立:

(48)

式中,M2，N2为ΔK的分解矩阵；ε2为方程可调参数.

当ε1>0,ε2>0,γ>0,对称矩阵X>0,Y>0,使得式(48)有解时,所求的状态反馈控制器为

Knf=YX-1

(49)

通过试凑法,首先随机选取M2,N2的数值,计算得到Knf,观察Knf与M2,N2矩阵的数值是否匹配,如果Knf与M3N2不匹配,则在仿真实验时,调整干扰信号的数值.最终得到M2,N2为

(50)

(51)

当ε1=1,ε2=1,γ=4时,得到非脆弱控制器Knf为

(52)

4.2 H∞鲁棒非脆弱控制器的数值模拟

获得控制器Knf后,设定系统输入为角阶跃信号,信号在第1 s时从0变化至0.05 rad,观察车辆的质心侧偏角、横摆角速度2个主要参数的变化,评估基于加法式摄动设计的非脆弱鲁棒控制器Knf的控制效果.Knf控制器基于加法式摄动来设计,加法式摄动定义为白噪声干扰,据此模拟系统的控制器存在干扰的情形.

图6为使用非脆弱控制器及脆弱控制器在加性摄动下的侧偏角响应.从图中可以看到,在侧偏角控制方面,非脆弱控制器的控制性能和脆弱控制器基本相同.在鲁棒性能方面,非脆弱控制器优于脆弱控制器,当系统控制器存在扰动时,非脆弱控制器可以保持系统输出稳定,没有剧烈波动.但非脆弱控制器在系统控制器存在扰动时,则波动十分剧烈.

图6 非脆弱控制器及脆弱控制器在加法式摄动下的侧偏角响应

图7是使用非脆弱控制器及脆弱控制器在加性摄动下的横摆角速度响应.可以看到,非脆弱控制器的控制性能与脆弱控制器基本相当.但在鲁棒性能方面差异较大,脆弱控制器在有控制器参数摄动的情况下,其输出值极其不稳定,波动幅度达到0.15 rad/s,非脆弱控制器则保持稳定,与没有扰动时的横摆角速度响应基本一致.说明在横摆角速度控制方面,非脆弱控制器鲁棒性能优异,而控制性能与脆弱控制器相当.

图7 非脆弱控制器及脆弱控制器在加法式摄动下的横摆角速度响应

5 结语

H∞鲁棒最优控制器在车辆系统参数变化情况下,既可以保证车辆系统的动力学性能优异,也可以保持较强的鲁棒性.可以同时兼顾稳定鲁棒性和性能鲁棒性.对于控制器参数存在变化的情形,H∞鲁棒非脆弱控制器的鲁棒性能非常卓越,优于未考虑控制器摄动的H∞鲁棒控制器.

References)

[1]Ozatay E, Unlusoy S Y, Yildirim M A. Design of fuzzy logic controller for four wheel steering system[C]//2005InternationalDesignEngineeringTechnicalConferencesandComputersandInformationinEngineeringConference. Long Beach,USA: American Society of Mechanical Engineers, 2005: 2331-2338. DOI:10.1115/detc2005-84114.

[2]Aslam J, Qin S Y, Alvi M A. Fuzzy sliding mode control algorithm for a four-wheel skid steer vehicle[J].JournalofMechanicalScienceandTechnology, 2014, 28(8): 3301-3310. DOI:10.1007/s12206-014-0741-y.

[3]Fahimi F. Full drive-by-wire dynamic control for four-wheel-steer all-wheel-drive vehicles[J].VehicleSystemDynamics:InternationalJournalofVehicleMechanicsandMobility, 2013, 51(3): 360-376. DOI:10.1080/00423114.2012.743668.

[4]胡国强. 汽车四轮转向系统转向特性的研究[D]. 武汉:武汉理工大学汽车工程学院,2012.

[5]Yin Guodong, Chen Nan, Wang Jinxiang, et al. A study on μ-synthesis control for four-wheel steering system to enhance vehicle lateral stability[J].JournalofDynamicSystemsMeasurementandControl, 2011, 133(1)： 011002. DOI:10.1115/1.4002707.

[6]Kolodziej J R. Adaptive rear-wheel steering control of a four-wheel vehicle over uncertain terrain [C]//ProceedingsoftheASME5thAnnualDynamicSystemsandControlDivisionConferenceandJSME11thMotionandVibrationConference. Fort Lauderdale, FL, USA: American Society of Mechanical Engineers, 2013: 857-866.

[7]Du H P, Lam J, Sze KY, et al. Design of non-fragile H-infinity controller for active vehicle suspensions[J].JournalofVibrationandControl, 2005, 11(2): 225-243. DOI:10.1177/1077546305049392.

[8]Gao X, Teo K L, Duan G R. et al. Non-fragile robustH∞control for uncertain spacecraft rendezvous system with pole and input constraints[J].InternationalJournalofControl, 2012, 85(7): 933-941. DOI:10.1080/00207179.2012.669848.

[9]Kchaou M, Souissi M, Toumi A. A new approach to non-fragileH∞observer-based control for discrete-time fuzzy systems[J].InternationalJournalofSystemsScience, 2012, 43(1): 9-20. DOI:10.1080/00207721003753409.

[10]Liu Zhenwei, Zhang Huaguang, Zhang Qingling, et al. Novel compensation-based non-fragileH∞control for uncertain neutral systems with time-varying delays[J].InternationalJournalofSystemsScience, 2012, 43(5): 961-971. DOI:10.1080/00207721.2010.543487.

[11]Xu H, Lin Z, Makur A, et al.Non-fragileH2andH∞filter designs for polytopic two-dimensional systems in Roesser model[J].MultidimensionalSystemsandSignalProcessing, 2010, 21(3): 255-275. DOI:10.1007/s11045-010-0104-5.

[12]祁永宁,陈南,李普,等.四轮转向车辆的直接横摆力矩控制[J].东南大学学报(自然科学版),2004,34(4):451-454. Qi Yongning, Chen Nan, Li Pu, et al. Direct yaw moment control of 4WS vehicle[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2004, 34(4): 451-454. (in Chinese)

[13]Fukui K, Miki K, Hayashi Y, et al. Analysis of driver and a ‘four wheel steering vehicle’ system using a driving simulator[J].SAETechnicalPaperSeries, 1988, 880641. DOI:10.4271/880641.

[14]Li Zhongjian, An Jinwen.Uncertainty representation and research of the application of high-performance robust flight controller dsign[J].JournalofNorthwestUniversity, 2002, 20(1): 96-99.

[15]You S S, Chai Y H.Multi-objective control synthesis: An application to 4WS passenger vehicles[J].Mechatronics, 1999, 9(4): 363-390. DOI:10.1016/s0957-4158(98)00056-7.

[16]Sun Ping.TheoryandapplicationofrobustH∞control[M]. Beijing: Tsinghua University Press, 2012: 36-46.

H∞robust controller design for 4WS-4WD vehicle based on LMI

Yin Guodong Wu Hao Zhang Ning Chen Jiansong

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

H∞robust optimal controller andH∞robust non-fragile controller were designed based on linear matrix inequality (LMI). Two degrees of freedom (2-DOF) vehicle model was used to derive and establish theH∞robust control system. In addition, the perturbation matrix of the system was defined and decomposed. And then the controller was obtained by using LMI. Simulation results show that the control effects on the sideslip angle and the yaw rate withH∞robust optimal controller are significantly better than those of LQR (linear quadratic regulator) controller. Meanwhile, when the perturbation of controller in the vehicle system exists, the control effects on side angle and yaw rate withH∞robust non-fragile robust are significantly better than those with of ordinaryH∞robust controller. Thus,H∞robust optimal control solves the problem with bad control performance forH∞robust control.H∞robust optimal control can guarantee control performance and robust performance at the same time.H∞robust non-fragile controller solves the problem that the controller is sensitive to parameters.

H∞robust control; linear matrix inequality; vehicle dynamics; optimal control; non-fragile control

10.3969/j.issn.1001-0505.2016.06.010

2016-02-03. 作者简介: 殷国栋(1976—),男,博士,教授,博士生导师,ygd@seu.edu.cn.

国家自然科学基金资助项目(51575103)、国家重点研发计划资助项目(2016YFB0100906,2016YFD0700905).

殷国栋,吴昊,张宁,等.基于LMI的4WS-4WD车辆H∞鲁棒控制器设计[J].东南大学学报(自然科学版),2016,46(6):1165-1171.

10.3969/j.issn.1001-0505.2016.06.010.

U461.1

A

1001-0505(2016)06-1165-07