中心椭圆光子晶体光纤高双折射以及色散的研究*
2016-12-15谷芊志励强华
谷芊志,励强华
(哈尔滨师范大学)
中心椭圆光子晶体光纤高双折射以及色散的研究*
谷芊志,励强华**
(哈尔滨师范大学)
提出一种新型中心椭圆高双折射光子晶体光纤,并采用有限元对不同椭圆率下的基模模场、双折射、有效折射率以及色散数值模拟.结果表明:通过改变不同中心椭圆的椭圆率的大小,在波长为1550μm,椭圆率为0.4的情况下,该光纤可以实现1.83×10-3的高双折射.并且通过对光纤中心的椭圆空气孔不同椭圆率的控制可以有效的控制该光子晶体光纤的有效折射率以及色散特性.该文对于高双折射光子晶体光纤的制备有着重要的意义.
光子晶体光纤;高双折射;有效折射率;色散
0 引言
光子晶体光纤(photonic crystal fiber,PCF)主要分为全内反射导光型光子晶体光纤以及光子带隙型光子晶体光纤.通过对光子晶体光纤中充入不同规律的空气孔,改变其对称性就可以得到高双折射特性以及其它一些重要的光学性质.近年来,由于PCF的高度可调特性,以及可控的结构,激发了许多研究者的兴趣. 2011年王伟[1]等提出了一种八边形高双折射双零色散点光子晶体光纤,该结构包层为圆形空气孔按亲照八边形状排列而成,并在包层对称位置中加入两个椭圆空气孔以获得高双折射特性,因此在波长0.8~2 μm的范围时双折射可以达到10-3数量级,满足高双折射的要求.2014年王二垒[2]等设计了一种高双折射高非线性多零色散波长光子晶体光纤.主要通过在纤芯处引入一排椭圆空气孔,并将中心处椭圆空气孔一分为二,从而获得了较高的高双折射.2012年黎薇[8]设计的高对称性模场分布的高爽折射光子晶体光纤为该文的模型的高双折射提供了理论依据.
该文以有限元法[3]为基本理论,通过设计优化对三角型结构排列的光子晶体光纤中心包层处的空气孔的不同椭圆率改变,来实现1.83×10-3的高双折射.并研究改变空气孔椭圆率来观察该光纤中心处模场的变化,以及不同椭圆率下的有效折射率及色散的改变情况.该光纤易于制造,并且具有10-3的高双折射.该文为研究类似模型,制备高双折射光子晶体光纤的实现提供了重要理论的依据基础.
1 模型仿真与结果分析
近年来,一些学者提出了八边形结构的光子晶体光纤[6]和六边形结构的光子晶体光纤以及V型结构的光子晶体光纤[5],以及双芯光子晶体光纤[7].该文设计了一种800~1550 nm波段的三角晶格结构六边形空气包层的光子晶体光纤.由图1可知,通过改变该光子晶体光纤中心包层处的包层,由圆形结构变成椭圆形结构,并以光子晶体光纤中心处为中心形成一个圆形环绕结构.光在纤芯中传播,通过改变纤芯外层处的椭圆率可得到较高的高双折射特性以及色散特性.其中椭圆空气孔间距Λ=1.2 μm,外包层的圆形空气孔直径a= 0.8μm.其中椭圆率用η=c/b表示,c表示为短直径,b为长直径.椭圆空气孔的长直径为b=1μm,逐渐改变短直径c从0.4到1.0μm.随着空气孔椭圆率变化研究该新型PCF的基模模场、有效折射率、高双折射以及色散特性的变化.

图1 中心椭圆型PCF端面结构
1.1 椭圆率η对基模模场的影响
有限元法是基于麦克斯韦方程组,导出光子晶体光纤中的电磁波的方程为[2](1)
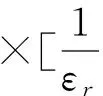
(1)
在该公式中H为磁场强度,εr和μr分别为介质的介电常数和磁导率,ω为光波的角频率,c是真空中光速.基于此利用有限元法建立合理的模型.控制孔间距Λ=1.2μm不改变且在1.55μm波长下,外包层的直径a以及椭圆长直径b也不改变时,改变椭圆包层处短直径c的大小,计算出光场分布.取四个特定数值进行比较,c分别为0.4、0.6、0.8、1.0,也就是改变椭圆率η分别取0.4到1.0时,进行数值计算.由图2可以看出在椭圆率η为0.4到1.0 情况下,光纤的基模模场被有效的限制在光纤的包层中心处.而图2(e)为a=b=0.4且椭圆率η=1.0的情况下光纤基模模场的形式.从该图中可以看出在a、b半径都为0.4的情况下基模模场虽然被限制在中心处但由于孔间距较大,使得场在中心处有较小的泄露.而(a)、(b)、(c)、(d)四种情况下长直径b未改变减小了中心处的孔间距,使得场被很好的限制在光纤的中心处.并且随着椭圆率的逐渐增大基模模场在逐渐的变小束缚在中心处.主要是因为随着中心处空气孔包层的逐渐增大,沿x方向以及y方向上的有效折射率在逐渐的减小,使得光纤基模模场逐渐变小,从而使得模场更加的集中.因此这在一定的程度上降低了光纤的功率损耗.

图2 1.55μm处波长下不同椭圆率下的基模模场对比(a) η=0.4 (b) η=0.6 (c) η=0.8 (d) η=1.0 (e) η=1.0 a=b=0.4
1.2 不同椭圆率下的基模有效折射率
由于光子晶体光纤的基模有效折射率neff与波长λ有关[10],所以在改变不同波长条件下的模型,可得到该光子晶体光纤在不同波长条件下的基模有效折射率.在孔间距为Λ=1.2μm时,外包层直径a=0.8μm椭圆包层长直径b=1.0μm时.如图3为改变椭圆的椭圆率η分别为0.4到1.0时,随着椭圆率的逐渐增大,该模式下的基模有效折射率在逐渐的减小.这是由于在不同椭圆率下,空气孔的填充率不同,因此才会导致基模有效折射率的改变.因此通过控制不同大小的椭圆率的变化,使得有效折射率更易于控制.
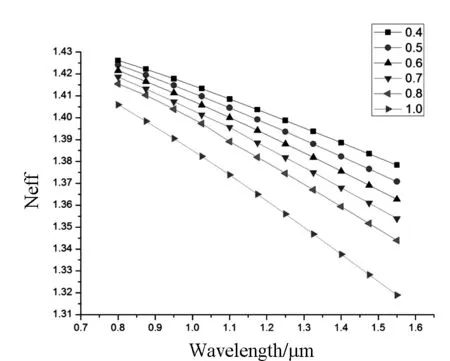
图3 不同椭圆率下基模有效折射率与波长关系
1.3 双折射特性
因为大部分光子晶体光纤的几何形状不具有对称特性,或是受力不均匀导致光纤中存在着几何双折射与应力双折射现象.这里双折射用B表示为模式双折射,B即为x方向和y方向基模有效折射率的差.模式双折射B是衡量光纤偏振特性的重要参数,可以表示为[4,9,12,15]
(2)


图4 不同椭圆率下的双折射与波长的关系
1.4 不同椭圆率下的色散关系
光子晶体光纤的色散D主要由两部分组成,即波导色散Dw(λ)和材料色散DM,D可以表示为[11]
D=DW(λ)+DM(λ)
(3)
其中利用有效折射率nneff的实部可得到该模式下对应的光纤的波导色散公式为[13-14]
(4)
λ为光在真空中的波长.材料色散DM主要由光纤本身的材料性质所决定,而光子晶体光纤通常采用纯石英材料与普通光纤的材料相同,因此光子晶体光纤的材料色散DM与普通光纤的材料色散DM相同.而波导色散主要是波长λ与有效折射率nneff的函数.因此由公式(4)结合Sellmeier公式来计算,并结合MATLAB进行数值模拟可得到图5色散与波长关系的曲线.其中当椭圆率η为0.4时在波长为1.375μm时得到一个零色散点,逐渐增加椭圆率η为1.0时零色散点在1.225附近处.因此随着椭圆率η的增加色散出现了红移.而零色散点的出现为光通信提供了重要的便利.因为激光光源在1300~1500nm的波长和单模光缆可构成大型网络的基础.而该文章通过对椭圆率的控制来实现在1300~1500nm处的零色散,可有效的为光通信的传输提供重要的理论依据.

图5 不同椭圆率下色散曲线
2 结论
该文设计了一种中心椭圆光子晶体光纤,利用有限元法并结合MATLAB进行数值模拟分析了该光纤的基模模场、双折射、有效折射率以及色散.分析结果表明,当孔间距 =1.2μm时,且控制外包层直径a=0.8μm椭圆包层长直径b=1.0μm不变,逐渐改变椭圆包层短直径c,即改变椭圆的椭圆率η分别为0.4到1.0,步长为0.1时.在椭圆率为0.4的情况下,该光纤可以实现1.83×10-3的高双折射.提高了保偏光纤的偏振质量.进一步通过控制椭圆率的大小,实现了色散的红移,对光纤的超连续谱的产生和零色散点的控制提供了重要依据.该以其高双折射特性以及色散色散特性为其应用在光通信,及一些光纤传感方面提供了重要的理论依据.
[1] 王伟,杨博,宋鸿儒,等.八边形高双折射双零色散点光子晶体光纤特性分析[J].物理学报,2012, 61(14):144601-144606.
[2] 王二垒,姜海明,谢康,等.一种高双折射高非线性多零色散波长光子晶体光纤[J].物理学报,2014,63(13):134210-134215.
[3] 凤兰.基于有限元法的光子晶体理论[J].内蒙古石油化工,2015(20):25-26.
[4] 玛依拉木.木斯得克,姚建铨,陆颖,等.1.55μm高非线性高双折射光子晶体光纤[J].光学精密工,2014,22(3):588-596.
[5] 夏长明,周桂耀,韩颖,等.V形高双折射光子晶体光纤特性研究[J].物理学报,2011,60(9):094213-094218.
[6] 李春莹,占雪梅,熊磊.八边形掺氟椭圆纤芯的光子晶体光纤设计研究[J].光学技术,2016,42(2):172-176.
[7] 郭士亮,胡春海,黄惠,等.碲玻璃双芯光子晶体光纤耦合特性研究[J].光子学报,2015,44(1):106001-106005.
[8] 黎薇,陈辉,陈明.高对称性模场分布的高双折射光子晶体光纤[J].中国激光,2012 ,39(2):205002-205005.
[9] 李珊珊,张昊,白晋军,等.隔行分层填充的太赫兹超高双折射多孔光纤[J].物理学报,2015,64(15):154201-154209.
[10] 李丽君,来永政,曹茂永,等.光纤纤芯及包层模有效折射率计算及仿真[J].物理学报,2013,62(14):140201-140205.
[11] 曹晔,王江昀,童峥嵘.基于微结构纤芯的超低损耗多零色散点的高双折射光子晶体光纤[J].中国激光,2013,40(9):905005-905010.
[12] 吴宵宵,范万德,廖文英,等.石墨烯包层结构光子晶体光纤的高双折射特性[J].光子学报,2013,45(1) :106002-106005.
[13] 付博,李曙光,姚艳艳,等.双芯高双折射光子晶体光纤耦合特性研究[J].物理学报,2009,58(11):7708-7715.
[14] 周铭皓,黄勇林.椭圆高双折射光子晶体光纤的双折射及损耗研究[J].光子学报,2016,45(3):0306002-306005.
[15] 曹晔,李荣敏,童峥嵘.一种新型高双折射光子晶体光纤特性研究[J].物理学报.2013,62(08):084215-084220.
(责任编辑:李家云)
The Research on High Birefringence and Dispersion of Center Ellipse Photonic Crystal Optical Fiber
Gu Qianzhi, Li Qianghua
(Harbin Normal University)
In this paper, a new center ellipse high birefringence photonic crystal fiber is presented, and the finite element are used to numerically simulate under the different ellipticity of fundamental mode field, birefringence, effective refractive index and dispersion. The results show that the fiber can achieve 1.83×10-3of high birefringence with changing the rate of different central ellipse ellipse size which the wavelength to 1550μm, the ellipticity is 0.4. And through to the center of the optical fiber with elliptical air holes and different ellipticity of control, the photonic crystal fiber effective refractive index and dispersion characteristics are controlled. To high birefringence photonic crystal fiber (PCF), it is an important significance.
Photonic crystal fiber; High birefringence; Effective index; Dispersion
2016-04-24
*黑龙江省自然科学基金(ZD201401)
TN253
A
1000-5617(2016)03-0049-04
**通讯作者:lqh0118@126.com
