边界条件对半球壳准静态屈曲行为的影响
2016-12-15胡建星杨会伟路国运
胡建星,徐 乐,杨会伟,张 恩,路国运
(太原理工大学 a.应用力学与生物医学工程研究所,b.材料强度与结构冲击山西省重点实验室,c.建筑与土木工程学院,太原 030024)
边界条件对半球壳准静态屈曲行为的影响
胡建星a,徐 乐a,杨会伟a,张 恩a,路国运b,c
(太原理工大学 a.应用力学与生物医学工程研究所,b.材料强度与结构冲击山西省重点实验室,c.建筑与土木工程学院,太原 030024)
对304不锈钢半球壳进行了2种边界条件下的准静态压缩实验,实验结果发现了2种不同的变形模态:环扣边界下的变形模态为六边形,自由边界下为五边形。为了探究边界条件对半球壳准静态压缩响应影响的内在规律,利用有限元技术,通过设置壳底部和底板接触摩擦系数的不同,研究了半球壳在3种边界条件下的准静态响应;并对载荷-位移曲线、半球壳变形轮廓图的变化以及顶点位移与加载位移之间的关系进行了比较分析。结果表明,摩擦系数为0.1和0.2时的半球壳压缩过程可以分为顶点压平、轴对称凹陷、非轴对称凹陷和顶点触底后再次压4个阶段;摩擦系数为0.5时,半球壳压缩过程可以分为顶点压平、轴对称凹陷、半球壳底部屈曲3个阶段。
半球壳;边界条件;准静态响应;塑性铰;变形模态
由于薄壳结构被广泛的使用,它的力学行为引起了国内外学者们的关注,其研究主要集中在沿球壳旋转轴方向的准静态加载或是动态加载条件下的塌陷行为,其中不乏大量的实验研究及理论研究。JOHNSON et al[1]对准静态加载下球壳的塌陷模态和相关的载荷-位移曲线进行了评述,并对其耗能机制进行了研究。UPDIKE et al[2-3], KITCHING et al[4], DE OLIVEIRA et al[5], KINKEAD et al[6]and GUPTA et al[7]分别于不同时期对半球壳在两块平行刚性板之间的轴向压缩进行了实验及理论研究,根据实验结果提出了不同的理论模型来预测球壳变形过程中载荷-位移的关系及吸能特性:UPDIKE et al[2-3]利用两个刚性板挤压半球壳的加载方式,研究了半球壳大变形的行为,即典型的后屈曲问题[8],分别讨论了半球壳材料为完全弹性和理想塑性时压缩载荷-位移的关系;KITCHING et al[4]根据半球壳的压缩实验结果将球壳压缩过程分为三个阶段:顶点压平阶段、轴对称凹陷阶段和非轴对称凹陷阶段;DE OLIVEIRA et al[5]根据两个塑性铰圆的假设研究了球壳在点载荷及质量块载荷作用下的轴向压缩力-压缩位移的关系;KINKEAD et al[6]考虑了应变强化效应研究了半球壳径厚比r/t为8-32时的准静态行为;GUPTA et al[7]提出了一种基于滚动塑性铰和固定塑性铰假设的理论模型(其中滚动塑性铰描述了球壳的轴对称变形、固定塑性铰描述了球壳的非轴对称变形),预测了球壳轴向压缩力和压缩位移之间的关系,与实验结果吻合较好;POGORELOV[9]和CALLADINE[10]在20世纪80年代从不同的角度出发给出了半球壳在准静态压缩和局部动态冲击时载荷-位移的关系,并研究了球壳残余变形的问题。杨桂通等[11]用空气动力枪对径厚比比较大的扁球壳在冲击载荷作用下的残余变形进行了实验研究,发现随着冲击能量的增大,壳体的残余变形逐渐增大。宁建国等[12-13]利用球壳的镜面反射模型[9]假定,分别得到了球壳材料为弹性和理想刚塑性假定时球壳残余变形的控制方程,通过数值求解分别与杨桂通等人的实验数据[11]进行了比较,其中理想刚塑性理论解吻合的更好。马春生等[14]研究了径厚比比较大的薄壁扁球壳撞击刚性板的动态响应和吸能特性,结合宁建国等[13]的大变形薄壳理论和塑性铰[7]方法建立了撞击力与变形的关系,以及撞击速度与最大压缩位移的理论分析模型,理论计算与其实验结果吻合较好。路国运等[15]对不同径厚比的半球壳在子弹冲击和落锤冲击作用下的动态响应进行了实验研究。GUPTA et al[16-19]在21世纪初期,同样对半球壳在质量块动态冲击加载条件下的压溃机理和吸能特性进行了比较系统的实验研究。
上述学者们对球壳响应的研究都没有对半球壳所处的边界进行特别的说明。SINGACE和ELSOBKY[20]研究了锥壳在不同边界约束下的轴向冲击响应,张善元等[21]研究了柱壳在两种不同边界下的动态响应,发现边界条件对柱壳屈曲模态影响非常大。本文旨在分析不同边界条件对半球壳变形模式的影响,通过准静态实验描述了不同边界下半球壳变形模式的不同,并借助有限元技术具体分析了边界条件影响半球壳变形模式的内在机理,从而为薄壳结构屈曲模式分析提供一定的参考依据。
1 实验研究
采用SUMSCMT 5105A微机控制电子万能实验机对304不锈钢半球壳进行了平板加载压缩试验,加载速率2 mm/min;研究了同种规格的半球壳在不同边界条件下的准静态响应,分析了实验得到的载荷-位移曲线,以及半球壳的最终变形模态,加载装置如图1所示。
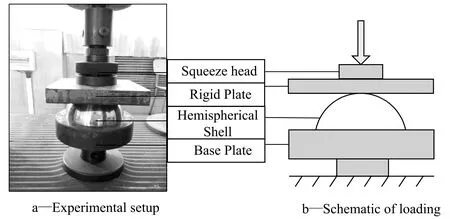
图1 实验装置及示意图Fig.1 Experimental setup and schematic
试验中所用到的球壳尺寸为半径75 mm,壁厚1.2 mm及试件加载条件见表1所示,实验设计了两种不同的边界条件(自由边界:直接把半球壳放在平面底座上,如图2-a;环扣边界:将半球壳放在底座上的沟槽里,如图2-b),而且为了证明实验的可靠性,每种边界条件都做了重复实验,从实验得到的载荷-位移曲线和半球壳的最终变形模态(如图3所示)来看,重复性相当好。
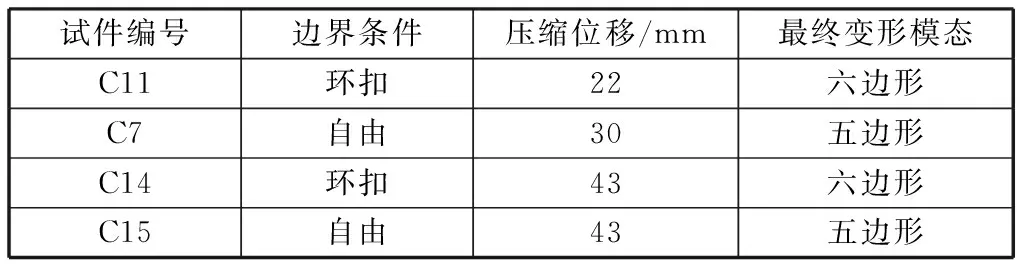
表1 实验条件和结果
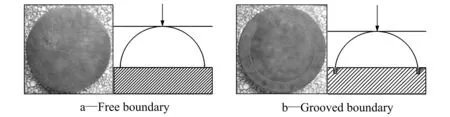
图2 加载条件Fig.2 Loading condition
图3给出了实验的载荷-位移曲线和及半球壳最终的变形模态。由表1和图3-a可以看到,边界条件对半球壳在平板压缩加载条件下的最终变形模态是有影响的。环扣边界的两个试件C11和C14最终变形都为六边形模态,而自由边界的两个试件C7和C15的最终变形都为五边形模态。
试件C11和C14的加载条件一样,都为环扣边界条件,加载板的位移分别为22 mm和43 mm .从实验结果观察到两个试件都发生了由轴对称凹陷到非轴对称凹陷的过渡,最终形成了六边形模态,该六边形模态是由中心窝陷区域,棱区,固定塑性铰和固定塑性铰之间形成的隆起4部分组成。比较C11和C14最终的变形模态可以发现,随着压缩位移的增加,固定塑性铰之间的隆起变得越来越明显,棱区还伴有扁平化趋势。从实验对半球壳压缩变形过程的观察还发现非轴对称发生后,形成多边形模态的边数没有发生改变。
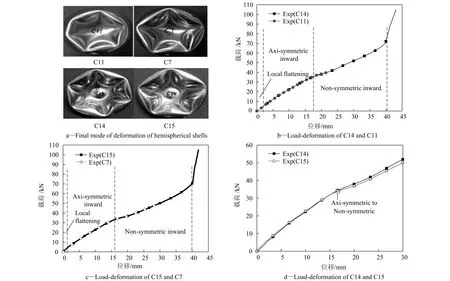
图3 载荷位移曲线和半球壳的最终变形模态Fig.3 Load deformation curves and final mode of deformation
图3-b给出了试件C11和C14的载荷-位移曲线,两者几乎重合,说明实验的重复性良好。从曲线上可以观察到曲线的斜率发生了3次明显的改变:第一次是半球壳顶点压平阶段到轴对称凹陷阶段的过渡,该阶段发生的时刻较早,基本上是在板的压缩位移和半球壳的厚度在同一个量级时就发生;第二次是轴对称凹陷阶段向非轴对称凹陷阶段的过渡,而且曲线的斜率变小,这是由于形成非轴对称凹陷时产生了许多的塑性铰,使得球壳抵抗变形的能力变弱,实验得到的载荷-位移曲线前两次斜率的改变与KITCHING et al[4]对半球壳压缩过程的分阶段相吻合;其中试件C14在加载板压缩位移为40 mm左右时突然急剧增加,斜率发生了第三次改变,这是由于半球壳压缩位移过大导致顶点触底和半球壳外围承载刚度增强共同造成的。
两个自由边界条件的试件C7和C15除最终变形模态为五边形外(如图3-a所示),实验得到的载荷-位移曲线(如图3-c所示)与试件C11和C14的基本类似。相同边界条件下,两个试件最终变形模态的一致性以及图3-b C11和C14的载荷-位移曲线和图3-c C7和C15的载荷-位移曲线吻合程度都可以说明实验的重复性是相当好的,即边界条件对半球壳的准静态响应是有影响的。
图3-d比较了两种不同边界条件下试件C14和C15的载荷-位移曲线,从图上可以看到:边界条件对半球壳压缩过程中的顶点压平阶段和轴对称凹陷阶段影响并不大,两者几乎是重合的;当轴对称凹陷阶段向非轴对称凹陷阶段过渡时边界条件开始产生影响,两者开始分离,虽然都伴有斜率的下降,但是自由边界比环扣边界下降的更多,前者形成了五边形,后者形成了六边形;在非轴对称凹陷阶段,环扣边界的半球壳抵抗变形的能力略大,形成多边形的边数也更多。至于半球壳在非轴对称凹陷阶段生成多边形的边数受什么因素控制还需进一步的研究。
2 数值研究
2.1 有限元模型的建立

图4 FEM模型中半球壳材料的应力-应变曲线Fig.4 Stress-strain curve with the piecewise linearity points for Numerical simulation
本节运用通用有限元软件ABAQUS 6.10对半球壳在准静态下的压缩行为进行了数值研究,分析了边界条件对半球壳准静态响应的影响。半球壳的几何、材料参数分别如下所述:半球壳尺寸,半径r=75 mm、厚度t=1.2 mm;图4给出了简单拉伸实验获得的应力-应变曲线,弹性模量150 GPa、泊松比0.3、屈服应力404 MPa,以及后续的塑性行为利用分段线性表示。半球壳网格采用全局种子2.0 mm布局,选择减缩积分四节点S4R单元,自由化划分网格算法;底座和加载板利用离散刚体模型;加载板、半球壳和底座之间的接触分别为:半球壳与加载刚性板之间的面面接触、半球壳的自接触和半球壳与底座之间的面面接触。通过控制刚性加载板位移实现对半球壳的准静态加载。
与实验相异的是不同边界条件的实现。实验是通过把半球壳分别放在平面底座和带有沟槽的底座上来实现两种不同的边界条件;数值模拟是通过改变半球壳和底座之间的摩擦系数来实现多种不同的边界条件,根据大量的试算结果,本文选择了三种摩擦系数下半球壳的准静态响应,分别为:A1摩擦系数为0.1,A2摩擦系数为0.2,A3摩擦系数为0.5 .
2.2 半球壳变形模态的比较

图5 不同边界条件下半球壳的最终变形模态Fig.5 Top-view and Front-view of the final deformation of hemispherical shells with different boundary
图5给出了3种边界条件下半球壳最终变形模态的俯视图(Top-view)和正视图(Front-view).从俯视图的不同,我们可以看出摩擦系数0.1时为五边形模态;摩擦系数0.2时为六边形模态;摩擦系数0.5时为轴对称模态。这也可以从相应的正视图加以解释,当摩擦系数为0.5时,由于半球壳底部与底座之间非常大的摩擦力,使得半球壳还来不及由轴对称模态过渡到非轴对称模态,球壳底部附近就发生了明显的屈曲,使得后面的响应过程主要是由底部附近的屈曲为主;而当摩擦系数为0.1和0.2时,球壳底部并没有发生屈曲,压缩过程中都发生了轴对称模态到非轴对称模态的过渡,但由于半球壳与底座之间摩擦系数的不同,导致半球壳在压缩过程中内力分布的差异,使得最终多边形模态的边数不一样;摩擦系数越大,半球壳在后期的压缩过程薄膜内力增加得越快,从而导致生成的多边形模态的边数越多。
2.3 变形轮廓、载荷-位移曲线的比较
图6-a、图6-b、图6-c分别给出了半球壳在不同摩擦系数的底座上,压缩过程的变形轮廓图,其中左边给出的是半球壳在压缩过程中变形轮廓的变化图,右边分别给出了相应变形轮廓的截面。
图6-a给出了半球壳与底座之间摩擦系数为0.1(A1)时的变形轮廓图。从图上可以看出,在整个压缩过程中,A1主要有4个阶段:顶点压平阶段(1.35 mm)、轴对称凹陷阶段(18 mm)、非轴对称凹陷阶段(42.53 mm)以及顶点触底后再次压平阶段(43.93 mm)。前3个阶段最早是由学者KITCHING et al[4]在1975年根据实验结果提出,并与实验得到的载荷-位移曲线上斜率两次明显的变化相对应。第一次为顶点压平阶段过渡到轴对称凹陷阶段,该过渡一般发生较早,当加载板压缩位移达到半球壳厚度时即有可能发生[5];第二次为轴对称凹陷阶段过渡到非轴对称凹陷阶段,这个过渡发生的条件比较复杂,半球壳的几何参数以及材料参数、载荷参数等对其都有影响,而且当半球壳厚度足够大时,该过渡将不会发生[16]。第4个阶段ALI DADRASI[22]在其文献中有过报道,A1当加载板位移为42.53 mm时,顶点与底座发生接触,并从载荷位移曲线上可以看到一个明显的变化,载荷突然急剧增加。

图6 不同边界下半球壳的变形轮廓图Fig.6 Deformation contour of A1,A2 and A3
从图6-a给出的变形轮廓图还可以明显发现左右并不对称,这可以利用右边的截面示意图加以解释:变形轮廓图的左、右显示的分别是多边形模态的边长和顶点处截面的变形轮廓变化;多边形模态边长处截面的变形轮廓在整个压缩过程中都没有发生外扩的迹象,而顶点处的变形轮廓当加载板位移为27 mm时即出现了非常明显的外扩趋势,从半球壳压缩过程可以看到这主要是因为在多边形的顶点处,随着加载板位移的增大,顶点临近的两条边不断地挤压顶点,从而使得多边形顶点不断地外扩;当加载板位移为42.35 mm,即半球壳顶点和底座发生接触时,多边形顶点下部发生了明显地向内屈曲的现象,图5最终变形模态的正视图也可以看到此现象。
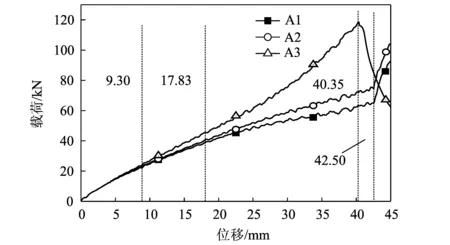
图7 不同边界下半球壳载荷-位移曲线的比较Fig.7 Load deformation curves of A1,A2, and A3
图6-b给出了半球壳与底座之间摩擦系数为0.2(A2)时的变形轮廓图。同A1一样的是,A2的整个压缩过程也主要由四个阶段组成,每个阶段对应的加载板压缩位移也基本相同。当加载板位移为1.35 mm(半球壳厚度为1.2 mm)时,发生了第一个过渡(从顶点压平阶段过渡到轴对称凹陷阶段),从图7的载荷-位移曲线图也可以观察到加载板位移为1.35 mm的时候,斜率发生了明显的变化。当加载板位移为17.83 mm时,A1和A2的载荷-位移曲线开始分离,且A2的载荷明显大于A1的载荷。这可以总结为:第一,半球壳与底座之间摩擦系数的大小对半球壳压缩初期并没有影响,只有当压缩到一定程度后,半球壳的边界条件才开始对压缩过程产生影响,与本文的实验结果相符,这也可以说明UPDIKE et al[2-3],DE OLIVEIRA et al[5],GUPTA et al[7],POGORELOV[9]等学者提出不考虑边界条件的半球壳响应理论在一定范围内是合理的;第二:半球壳压缩过程的第二个过渡(轴对称凹陷阶段过渡到非轴对称凹陷阶段)发生于加载板压缩位移为17.83 mm,而此时正好是边界条件开始对半球壳压缩过程产生影响的时候,说明对于A1和A2来说边界条件对半球壳压缩过程是从第二个过渡阶段开始产生影响,并影响其后面的变形模态。底部约束越强,半球壳在非轴对称凹陷阶段的抵抗变形的能力也越强,形成多边形模态的边数也越多:A1和A2分别为五边形模态和六边形模态。
图6-c给出的是半球壳与底座之间摩擦系数为0.5(A3)时的变形轮廓图。与A1和A2的4个阶段变形模式不同的是,A3的整个压缩过程只有3个阶段:第1个阶段与A1和A2一样,属于顶点压平阶段,加载板位移都为1.35 mm;第2个阶段一直持续到加载板位移为40.35 mm左右,从图7的载荷-位移曲线可以观察到当加载板位移为40.35 mm时,载荷突然急剧减小,过渡到第3个阶段。从A3的变形轮廓图可以观察到:A3的第2个阶段发生的变形也是轴对称凹陷,但不同的是,当加载板位移为17.83 mm时,A1和A2开始由轴对称凹陷阶段向非轴对称凹陷阶段过渡, 而A3的整个响应过程一直是轴对称凹陷变形,但其载荷位移曲线在第2个阶段却发生了一个明显的变化,载荷由递减增加逐渐过渡到递增增加,这主要是边界的影响使得半球壳结构的刚度随压缩位移的增大而增大造成的。A3的第3个阶段载荷随着位移的增大迅速减小,这是由于底部发生了屈曲行为,从图6-c中的Stage-3可以观察到。
2.4 半球壳压缩过程顶点位移和加载板压缩位移的关系
图8给出的是三种摩擦系数工况下,半球壳顶点位移和加载板压缩位移之间的关系。从图8-a可以观察到A1和A2两种摩擦系数下半球壳顶点位移和加载板压缩位移关系曲线完全重合,说明:半球壳和底座之间的摩擦系数从0.1增加到0.2,载荷-位移曲线和半球壳的最终变形模态发生了变化,但顶点位移和加载板压缩位移关系并没有发生改变;以及轴对称凹陷阶段向非轴对称凹陷阶段过渡时,顶点位移和加载板压缩位移关系也没有发生变化。图8-b给出的是摩擦系数为0.5时,可以观察到在半球壳底部发生屈曲前,顶点位移和加载板位移关系与摩擦系数为0.1,0.2时的一样;当半球壳底部发生屈曲后,整个压缩过程由滚动塑性铰的扩展和底部屈曲变形共同组成。
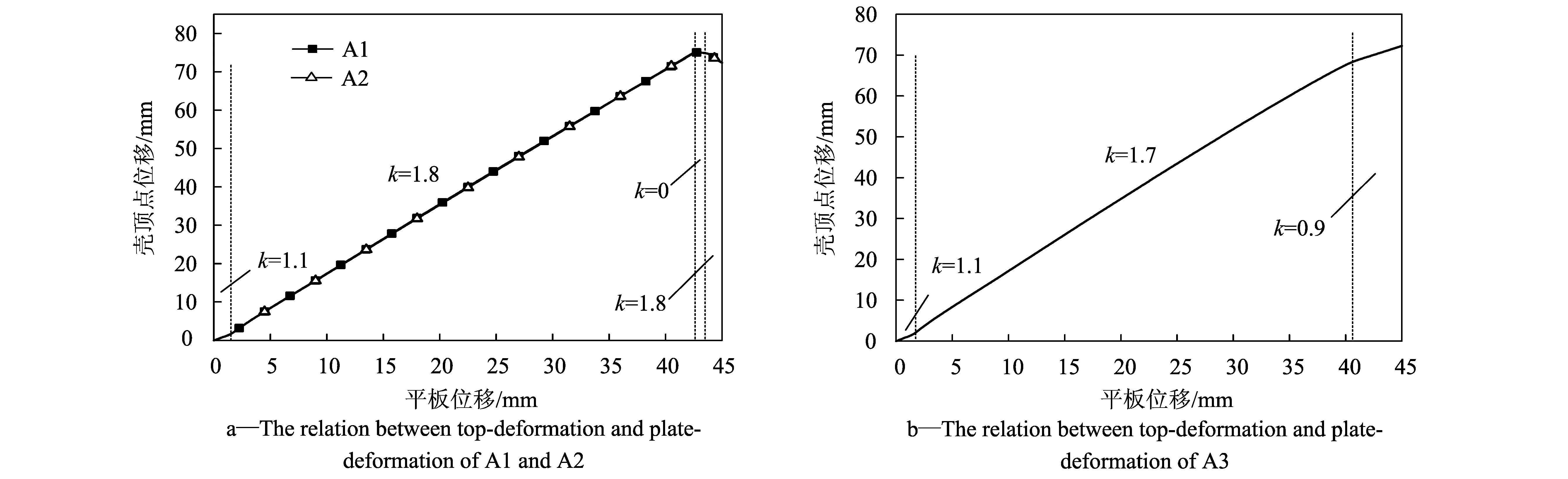
图8 平板压缩位移与球壳顶点位移的关系Fig.8 Relation between top deformation and plate deformation of A1, A2 and A3
3 结果与讨论
通过实验和数值模拟技术,研究了边界条件对半球壳准静态响应的影响,得到以下结论。
1) 半球壳在小变形的情况下,由于其结构的几何特性使其底部边界对其准静态响应的影响可以忽略,也能说明镜面反射模型的3部分变形区域假定是可接受的。
2) 半球壳在从轴对称凹陷阶段过渡到非轴对称凹陷阶段时,其顶点位移和加载板压缩位移之间的关系并不发生改变。
3) 从实验和数值模拟分别得到的不同边界条件下的载荷-位移曲线的比较发现:当半球壳的薄膜内力增加的越快,半球壳在发生非轴对称凹陷时产生的多边形的边数会越多。
[1] JOHNSON W,REID S R.Metallic energy dissipating systems[J].Appl Mech Rev,1978,31(3):277-288.
[2] UPDIKE D P,KALNINS A.Axisymmetric behavior of an elastic spherical shell compressed between rigid plates[J].Journal of Applied Mechanics,1970,37(3):635-640.
[3] UPDIKE D P.On the large deformation of a rigid-plastic spherical shell compressed by a rigid plate[J].Journal of Engineering for Industry,1972,94(3):949.
[4] KITCHING R,HOULSTON R,JOHNSON W.A theoretical and experimental study of hemispherical shells subjected to axial loads between flat plates[J].International Journal of Mechanical Sciences,1975,17(11):693-703.
[5] DE OLIVEIRA,JOAO G,TOMASZ WIERZBICKI.Crushing analysis of rotationally symmetric plastic shells[J].The Journal of Strain Analysis for Engineering Design,1982,17(4):229-236.
[6] KINKEAD A N,JENNINGS A,NEWELL J,et al.Spherical shells in inelastic collision with a rigid wall——tentative analysis and recent quasi-static testing[J].Journal of Strain Analysis for Engineering Design,1994,29(1):17-41.
[7] GUPTA N K,EASWARA PRASAD G L,GUPTA S K.Axial compression of metallic spherical shells between rigid plates[J].Thin-walled structures,1999,34(1):2141.
[8] SWIFT H W.Plastic instability under plane stress[J].Journal of the Mechanics and Physics of Solids,1952,1(1):1-18.
[9] POGORELOV A V.Bendings of surfaces and stability of shells[M].Providence RI:AMS,1988:113.
[10] CALLADINE C R.Analysis of large plastic deformations in shell structures[J].Springer Berlin Heidelberg,1986:69-101.
[11] 杨桂通.冲击载荷下结构动态行为的实验研究[J].力学学报,1990,22(4):374-379.
[12] 宁建国,杨桂通.球形扁壳在冲击载荷作用下的超临界变形[J].爆炸与冲击,1992,12(3):206-212.
[13] 宁建国,杨桂通.理想刚塑性球形薄壳在刚性柱体冲击下的破坏分析[J].北京理工大学学报,1997,17(5):545-551.
[14] 马春生,杜汇良,张金换,等.薄壁扁球壳在撞击载荷下的动态响应和吸能特性研究[J].振动与冲击,2007,26(1):4-7.
[15] 路国运,秦斌,张国权,等.冲击作用下夹层充液薄壁半球壳组合结构的动力响应[J].爆炸与冲击,2012,32(6):561-567.
[16] GUPTA N K.Experimental and numerical studies of dynamic axial compression of thin walled spherical shells[J].International Journal of Impact Engineering,2004,30(8):1225-1240.
[17] GUPTA N K,MOHAMED SHERIFF N,VELMURUGAN R.Experimental and numerical investigations into collapse behavior of thin spherical shells under drop hammer impact[J].International Journal of Solids and Structures,2007,44(10):3136-3155.
[18] GUPTA N K,MOHAMED SHERIFF N,VELMURUGAN R.Experimental and theoretical studies on buckling of thin spherical shells under axial loads[J].International Journal of Mechanical Sciences,2008,50(3):422-432.
[19] GUPTA P K,GUPTA N K.A study of axial compression of metallic hemispherical domes[J].Journal of Materials Processing Technology,2009,209(4):2175-2179.
[20] SINGACE A A,ELSOBKY H,PETSIOS M.Influence of end constraints on the collapse of axially impacted frusta[J].Thinwalled Structures,2001,39(5):415-428.
[21] 冀健龙,雷建平,张善元.两种边界条件下圆柱壳轴向冲击屈曲实验研究[J].科学技术与工程,2010,10(7):1740-1743.
[22] ALI DADRASI.Energy absorption of semispherical shells under axial loading[J].Australian Journal of Basic and Applied Sciences,2011,5(11):2052-2058.
(编辑:朱 倩)
Quasistatic Response of Hemispherical Shell with Different Boundary Condition
HU Jianxinga,XU Lea,YANG Huiweia,ZHANG Ena,LU Guoyunb,c
(a.InstituteofAppliedMechanicsandBiomedicalEngineering;b.ShanxiKeyLab.ofMaterialStrength&StructuralImpact;c.CollegeofArchitectureAndCivilEngineering;TaiyuanUniversityofTechnology,Taiyuan030024,China)
Two different deformation modes were observed from experimental results of the quasi-static response of hemispherical shell in different boundary condition. The deformation mode is six lobes for grooved boundary, but five lobes for free boundary. By utilizing the finite element method, the internal mechanism of effects of three different boundary conditions on quasi-static response of hemispherical shell was researched, and the loaded formation curves, transformation of deformation contour map of hemispherical shells and the relation between top displacement of hemispherical shell and loading plate displacement were compared.The results show: the compression process of hemispherical shell can be divided into four stages: local flattening, axisymmetric dimpling, non-axisymmetric dimpling and local flattening again when the friction coefficient between shell and plate is 0.1 and 0.2. However, when the friction coefficient is 0.5, the compression process can be divided into three stages: local flattening, axisymmetric dimpling and buckling of the bottom of shells.
hemispherical shell;boundary condition;quasi-static;plastic hinge;deformation mode
1007-9432(2016)03-0411-07
2015-10-13
国家自然科学基金资助项目:浆砌多级构建层合壳体的冲击动力学行为研究(11372209);山西省回国留学人员科研及择优资助项目(2013-044)
胡建星(1990-),男,江西九江人,硕士生,主要从事冲击动力学的研究,(E-mail)hjx3783@link.tyut.edu.cn
路国运,教授,博士生导师,主要从事冲击动力学和结构动力学方面的研究,(E-mail) luguoyun@tyut.edu.cn
O348.9
A
10.16355/j.cnki.issn1007-9432tyut.2016.03.025
