锚杆锚固系统应力波分形机制及其应用研究
2016-12-15冯剑锋赵金昌梁腾飞贾少华尹志强卞德存
冯剑锋,赵金昌,梁腾飞,贾少华,尹志强,闫 东,卞德存
(太原理工大学 矿业工程学院,太原 030024)
锚杆锚固系统应力波分形机制及其应用研究
冯剑锋,赵金昌,梁腾飞,贾少华,尹志强,闫 东,卞德存
(太原理工大学 矿业工程学院,太原 030024)
为研究锚杆振动系统应力波分形特性,采用分形理论的盒维数方法,建立了适用于锚杆振动信号的盒维数模型。结合锚杆工作荷载实验,计算得到了锚杆振动信号分形盒维数值D,从理论上探讨了锚杆振动信号波形的物理力学机制,解释了D与锚杆工作荷载之间的内在联系。研究表明,D与锚杆振动基频及锚固介质阻尼关系密切,振动基频反映了振动信号的不规则度和复杂度,而锚固介质阻尼直接影响振动信号的衰减,从而影响D的数值大小。将锚杆无损检测与分形理论结合,为锚杆无损检测分析领域提供了全新的研究思路。
锚杆锚固;应力波;盒维数;工作荷载;分形机制;基频;无损检测
目前,在地下工程施工中,采用锚杆加固围岩的方法已经被普遍应用。然而由于多方面原因,在工程现场对锚杆锚固质量进行检测时,大多仍采取破坏性试验的手段,这种检测方法不仅效率低下,而且会对周边围岩形成比较强烈的扰动,破坏围岩结构,大大弱化了锚杆的支护效果,这种弊端在岩层比较软或者遇到破碎岩层时尤为突出。因此,亟待探求一种方法,在不破坏围岩的前提下,对锚杆锚固质量进行快速、准确的判断。
随着对锚杆锚固系统振动特性的深入研究,发现锚杆锚固系统应力波作为各种频率成分简谐波的组合,其波形表现相当复杂;但在相同的锚固参数条件下,进行重复、多次实验所获取的振动信号波形参数,如频率、反射时间等参数基本相近,且满足统计自相似性随机分型特性[1]。分形理论作为一种新理论,近年来已经被引入到爆破振动信号、地震波信号的处理等研究领域。为了拓展分形理论在锚杆无损检测领域的应用,笔者提出将锚杆锚固系统振动信号的分形盒维数与锚杆工作荷载相结合,通过盒维数模型的建立、实验研究与理论分析,给出判断锚杆工作荷载的一个新思路。
1 盒维数模型定义
设锚杆锚固系统振动信号W(t)⊂F,F是n维欧式空间Rn上的闭集。Nδ是用来覆盖F所需边长为r的n维立方体最小数目,则W(t)的盒维数定义为[2-3]:
本次实验的数据采集仪在采集信号时是每间隔一段时间Δt采集一次信号,最后将采集到的所有数据点连成光滑曲线。因此,严格意义上来说,在一个采样时间间隔内,两个数据点之间是一段直线,因此在用长度为δ的盒子对集合F进行覆盖时,δ>Δt。在实际计算过程中,一般不根据盒维数的定义直接得到D,而是根据分形对象在其无标度区,将一系列尺寸为kδ(k为网格放大倍数)的方形网格对分形对象进行覆盖,从而计算出不同尺度下的有效覆盖网格数量Nkδ,采用最小二乘法得出lg(1/kδ)-lgNkδ的拟合直线,其斜率就是该波形的盒维数D[3]。
2 锚固系统振动信号盒维数计算模型
如图1所示的波形就是典型的锚杆振动信号波形。锚杆锚固系统振动信号包括两个尺度,纵向表示其振幅,横向表示时差。要对振动信号曲线进行较为准确的覆盖,必须建立与其相匹配的矩形盒模型,从而表征其特性[4]。本文采用的矩形盒模型尺度为δ1×δ2, 即横向×纵向。

图1 典型的锚杆振动信号Fig.1 Typical bolt vibration signal
如图2所示,试件全长L=1.6 m,锚固段长度L2=0.5 m,则固端反射时间
底端反射时间
取应力波在杆体中的传播速度v1=5 070 m/s,在锚固系统中的传播速度近似为v1=4 000 m/s,则振动信号包含固端反射和底端反射的时间可以确定。实验中的采样频率为500 kHz,所以时间间隔为

图2 试件示意图Fig.2 Schematic diagram of pieces
关于纵向尺度,由于其与振幅相关,而振幅又受到激发装置的激发冲量大小影响,所以没有一个固定的值。在实验过程中,我们尽可能地让每次激发的冲量相等。通过观察对比,得到最大振幅(振幅用电荷Q表示)差值为ΔQ<11 nC,故取ΔQ=11 nC.同时,为保证选取的数据点数能够完整包含一次固端反射和底端反射及显示首波,我们选取n=500个数据点,得到
在用矩形盒覆盖振动信号时,-lg(kδi)与lgNkδi满足线性回归方程:
盒维数计算式为[4-5]:
图3为本次实验中的一条拟合直线。
3 实验研究
实验选用3组试件。为研究锚固介质的阻尼对盒维数的影响,用介质的不同密实程度来模拟介质的不同阻尼,其他锚固参数相同。外径90 mm的钢管中的端锚锚杆,硅酸盐水泥型号425,用水泥与细沙质量比为1∶2的水泥砂浆作为锚固剂,水灰质量比1∶0.5,养护28 d后进行测试,试件参数见表1所示。

表1 试件参数
在MATLAB中,根据上述计算模型,对得到的加速度响应信号进行处理,如图3所示。
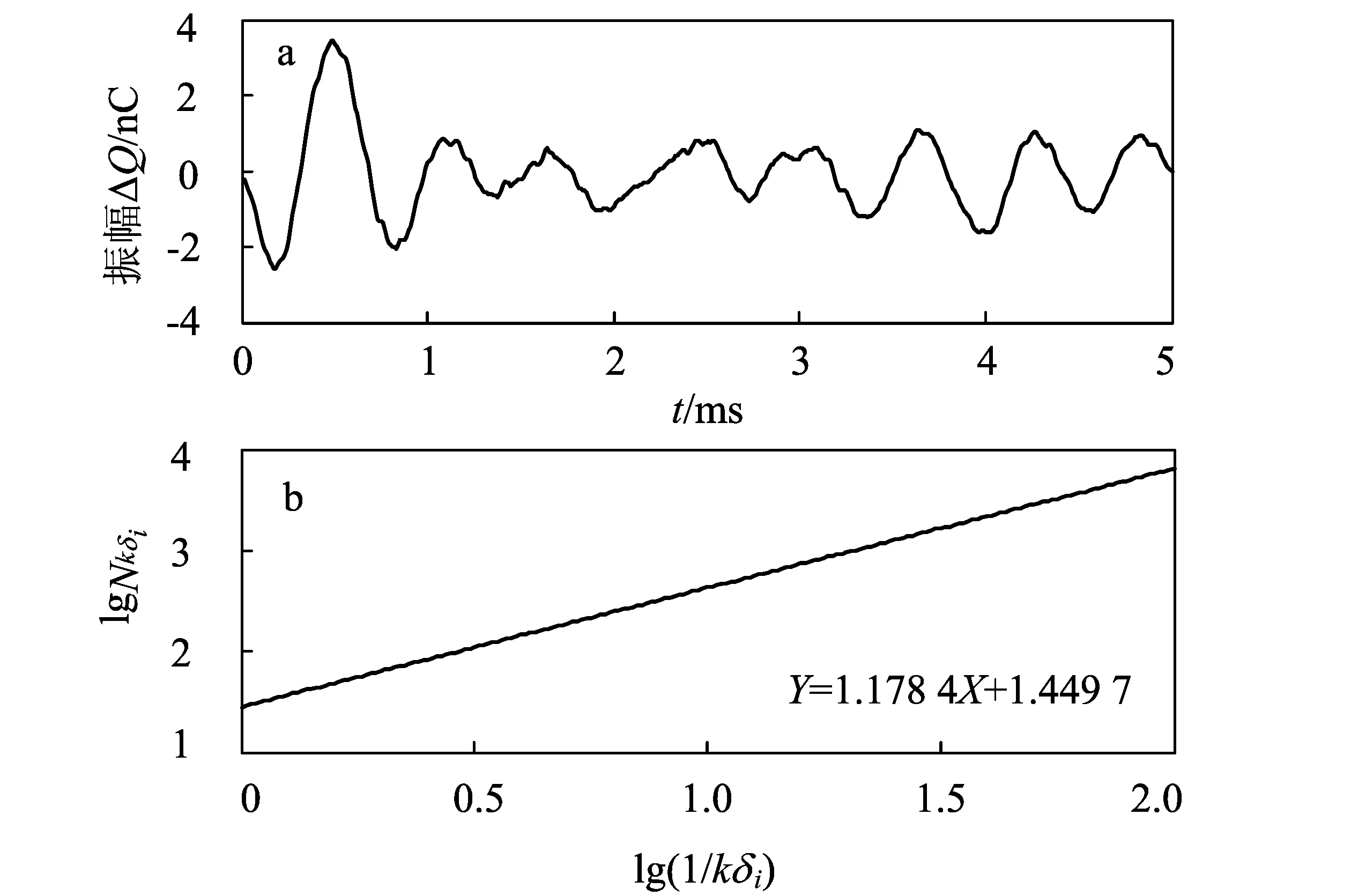
图3 盒维数拟合结果Fig.3 Box dimension fitting results
利用DAP软件提取信号基频[5]。DAP7.1瞬态测试分析软件是由成都泰斯特电子信息有限责任公司开发的一款用于瞬态信号测试、采集、分析和存储的软件,在数据处理方面有数字滤波器、时域处理、频域处理、特征值显示等功能。
针对此次实验数据,选择该软件的频域处理功能,对信号进行频域处理,处理类型选择幅值线性谱,其计算式为:
fft为快速傅立叶变换,其公式为:

加载函数选择Hanning,其公式为:

频域处理函数如图4所示。盒维数计算结果及基频见表2和图5所示。根据实验结果可得出如下结论。

图4 频域处理函数Fig.4 Frequency domain processing window

荷载/kN试件1试件2试件3盒维数D基频f/kHz盒维数D基频f/kHz盒维数D基频f/kHz01.13063.3201.09953.0271.10222.9351.13183.5161.10583.2231.11534.004101.14313.7111.11143.8091.11654.199151.14944.1021.11294.0041.12114.297201.15994.2971.11514.6881.12724.590251.16395.0781.11725.1761.13724.883301.16585.2731.11935.3711.14174.980351.16885.4691.12665.5661.14815.078401.17155.6641.13285.7621.15355.176451.15475.8591.14155.9571.16635.237501.16585.0781.11694.9801.13404.883551.13854.6881.11494.8831.12414.492601.13924.4921.11244.5901.11424.199
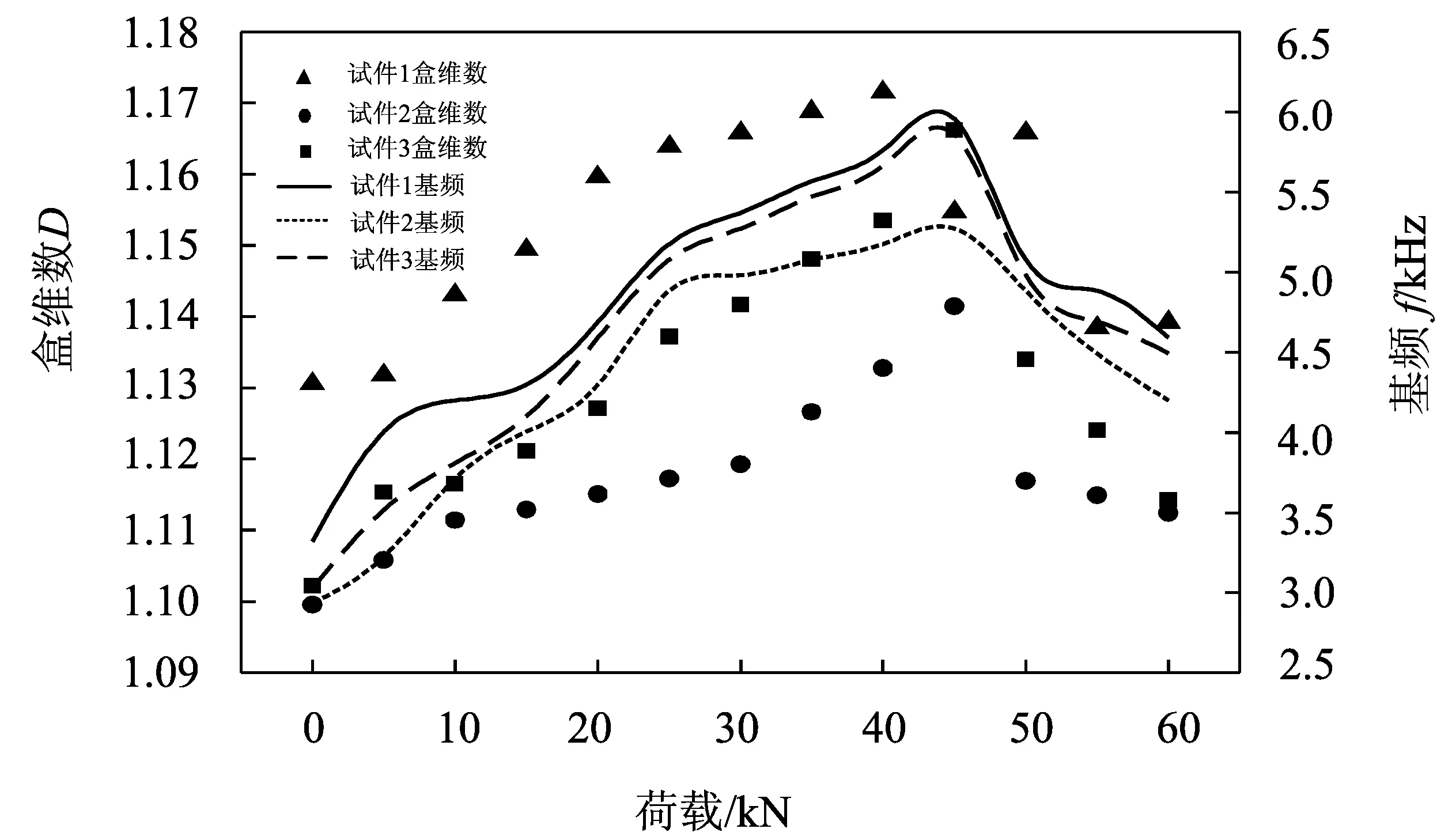
图5 盒维数、基频与荷载对应关系Fig.5 Relationship between box-dimension,the fundamental frequency and load
1) 从表2测试数据可以发现,3组试件基频值及盒维数值均以45 kN锚固失效点为拐点,如图5所示。荷载在0~45 kN阶段时,随着荷载的增加,锚杆振动基频值及振动信号盒维数值增大;荷载增加到45 kN以后,锚固体松动,水泥砂浆开始脱落,相应地锚杆振动基频值及振动信号盒维数值减小。
2) 由于3组试件锚固密实程度有差异,而锚杆的固有频率又受周围锚固介质抗剪强度的影响较大,故而其基频值也有相应差异。
3) 锚固介质的阻尼直接影响到锚杆振动信号的衰减,介质阻尼越大,信号越趋于平缓,表现在盒维数值上,即介质阻尼越大,盒维数值越小。故而3组试件的盒维数值大小关系为:
试件1>试件3>试件2 .
4 机理研究
由于锚杆锚固系统受力及振动情况相当复杂,为了便于计算,做出下列假设。
1)锚杆侧介质是均匀的。
2)用一个线性弹簧和一个与速度有关的阻尼器以平行方式耦合,以模仿锚杆周围介质与锚杆之间的相互作用。
3)围岩深度对锚杆周围介质的剪切应力不构成影响。
根据上述假设,结合理论分析,得出锚杆的工作荷载F与锚杆锚固系统振动基频f呈以下关系,即[6-10]:
式中:L为锚杆的长度;f为锚杆的振动基频;vc为激发应力波在锚杆杆体中的传播速度,取5 070m/s;E为锚杆杆体弹性模量;A为锚杆的横截面面积。锚杆为周围介质系统共同作用时得锚杆纵向波动方程[11-12]:
锚杆底端固定,顶端自由,则其振动边界条件为:
解得,加速度响应:
在实际振动测试时,加速度传感器固定在锚杆顶端,把x=L代入上式中可得:

综上,对于锚杆振动信号,其曲线复杂程度可以根据它的频率成分反映出来[10]。由上述的理论分析可知,应力波在激发状态下,随着锚杆工作荷载的增加,锚杆顶端反射加剧,锚杆振动基频随之增大;表现在振动信号上即信号趋于“复杂”,对应的信号变化加快;表现在波形图像上,即信号波形所占据的平面比例进一步增大;而盒维数恰恰是反映图形的复杂程度或不规则程度[13-15],相应地盒维数值增大。随着荷载的不断增加,当锚杆接近“拉脱”状态时,此时锚杆相当于锚固劣质的锚杆。由于杆体与周围介质粘结力减小及周围介质松动,周围介质的抗剪强度降低,锚杆振动基频减小[16-17],从而振动信号趋于“简单”,即对应的信号变化减慢,信号波形所占据的平面比例进一步减小,相应的盒维数值减小。
对于锚固介质阻尼不同的试件,由于介质阻尼直接影响到信号的衰减,故介质阻尼越大,信号衰减越快,表现在波形图像上,即信号波形所占据的平面比例进一步缩小,相应的盒维数值越小。
5 结论
1) 研究及实验表明,根据锚杆振动信号的特点与规律,结合分形理论对锚杆振动波形进行双尺度矩形盒维数建模可行、有效。
2) 对于同一根锚杆,随着锚杆工作荷载的增大,锚杆振动信号盒维数值增大,当锚固体出现松动,锚杆接近“拉脱”状态,即将要失效时,锚杆振动信号盒维数值随着工作荷载的增大而减小。
3) 以上盒维数值的变化是因为随着荷载的增加,锚杆振动基频增大,振动信号趋于复杂,盒维数值相应增大。直至锚固体出现松动,导致锚杆振动基频减小,振动信号趋于简单,盒维数值相应减小。
4) 对于不同的锚杆,振动信号盒维数值大小受锚固介质阻尼的影响较大,介质阻尼越大,振动信号盒维数值越小。
[1] 张济忠.分形[M].北京:清华大学出版社,1995.
[2] 朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011.
[3] 娄建武,龙源,徐全军,等.爆破地震信号的分形盒维数值分析[J].爆炸与冲击,2004,24(4):364-369.
[4] 晏俊伟,龙源,娄建武,等.爆破地震波的分形机制[J].解放军理工大学学报,2008,9(4):367-372.
[5] 梁腾飞,冯剑锋,卞德存,等.基于盒维数的锚杆工作荷载无损检测研究[J].太原理工大学学报,2015,46(3):327-331.
[6] 任智敏,李义.基于声波测试的锚杆锚固质量检测信号分析与评价系统实现[J].煤炭学报,2011,36(1):191-196.
[7] 刘海峰,杨维武,李义.锚杆工作荷载实时检测技术研究[J].矿业研究与开发,2008,28(2):54-57.
[8] 刘海峰.锚杆锚固系统及工作状态动测技术研究[D].太原:太原理工大学,2000.
[9] 李义,张昌锁,王成.锚杆锚固质量无损检测几个关键问题的研究[J].岩石力学与工程学报,2008,27(1):108-116.
[10] 刘海峰,李义.应力波反射法锚杆底端反射规律的实验研究[J].太原理工大学学报,2000,25(2):160-164.
[11] 李义,刘海峰,王富春.锚杆锚固状态参数无损检测及其应用[J],岩石力学与工程学报,2004,23(10):1741-1744.
[12] 李义.锚杆锚固质量无损检测与巷道围岩稳定性预测机理研究[D].太原:太原理工大学,2009.
[13] 王成.锚杆锚固质量动测新技术的研究[D].太原:太原理工大学,1998.
[14] 谢全民,龙源,钟明寿,等.小波与分形组合分析技术在爆破振动信号分析中的应用[J],振动与冲击,2011,30(12):120-124.
[15] 刘国华,黄平捷,龚翔.基于分形维和独立分量分析的声发射特征提取[J].华南理工大学报(自然科学版),2008,36(1):76-80.
[16] 谢全民,龙源,田作威.爆破振动信号时频特征的三维分形特征研究[J].振动与冲击,2010,29(12):122-126.
[17] 杨湖,王成.锚杆围岩系统数学模型的建立及动态响应分析[J].测试技术学报,2002,16(1):41-44.
[18] 李义,王成.应力波反射法检测锚杆锚固质量的实验研究[J].煤炭学报,2000,25(2):160-164.
(编辑:庞富祥)
Research on Fractal Mechanism of Bolt Anchor System Stress Wave and Its Application
FENG Jianfeng,ZHAO Jinchang,LIANG Tengfei,JIA Shaohua, YIN Zhiqiang,YAN Dong,BIAN Decun
(CollegeofMiningEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China)
For studying the stress wave fractal characteristics of bolt vibration system, using the fractal box-dimension method was used to, according to the propagation and characteristics of bolt vibration signal,establish the double scale rectangular box dimension model. Combined with the bolt working load experiments,calculations were carried out to obtain the bolt vibration signal fractal box dimension valuesD,the physical mechanism of anchor vibration signal waveform was theoretially discussed,and the relationship betweenDand the bolt working load was revealed.Research shows that,Dis close to the fundamental frequency and the anchoring medium damping, vibration fundamental frequency reflects the irregularity and complexity of the vibration signal, and the anchoring media damping directly affects the vibration signal attenuation,and thus affects theDnumerical size. Combining fractal theory with anchor nondestructive testing will provide a new research idea.
bolt anchor system;stress wave;box-dimension; working load;fractal mechanism;fundamental frequency;nondestructive testing
1007-9432(2016)03-0321-05
2015-10-30
国家自然科学基金资助项目:涵盖峰后大变形过程的巷道围岩与支护平衡规律及控制机理研究(51274145);教育部博士点基金资助项目:群锚结构锚杆荷载演化与围岩稳定性预测机理研究(20111402110003)
冯剑锋(1989-),男,山西泽州人,硕士生,主要从事结构无损检测方面的研究,(E-mail)15135151732@163.com
赵金昌(1974-),男,副教授,主要从事结构无损检测及水中高压脉冲放电方面的研究,(E-mail)zjc_8989@163.com
TD-05
A
10.16355/j.cnki.issn1007-9432tyut.2016.03.009
