提高飞行器姿态角计算精度的方法研究

范奎武，张　兵

（1．海军驻航天一院代表室，北京100076；2．北京航天自动控制研究所，北京100854）

提高飞行器姿态角计算精度的方法研究

范奎武1，张兵2

（1．海军驻航天一院代表室，北京100076；2．北京航天自动控制研究所，北京100854）

分析了传统的通过方向余弦矩阵、四元数形式的飞行器转动微分方程数值积分结果确定姿态角方法的不足，介绍了基于改进的牛顿法确定飞行器姿态角的方法。基于多次测量均值效应原理，介绍多使用上述两种方法中的元素提高飞行器姿态角计算精度的算法及仿真结果。

飞行器；姿态角；四元数；方向余弦；精度

0 引言

描述飞行器姿态的除了有欧拉角、方向余弦、四元数这3种常用的方法外，还有5元素法。欧拉角法简单，物理意义直观，但对于飞航式飞行器当俯仰角接近时会出现奇异点，从而使描述姿态运动的欧拉角微分方程发散。因此在实际求解飞行器转动微分方程时常使用后两种方法，然后再利用它们与欧拉角的关系换算出姿态角。但是在求解其余两种方法下飞行器的姿态变化微分方程时，随机误差会随时间积累，从而导致确定姿态角时的误差［1⁃3］。

本文介绍推导根据方向余弦矩阵和四元数的元素提高姿态角计算精度的算法和仿真确认结果［4］。

1 确定飞行器姿态的方法简介

用体轴坐标系Oxbybzb相对发射惯性系Oxiyizi的姿态表述飞行器的姿态。以倾斜发射的飞行器为例，设由发射惯性系Oxiyizi绕Oyi轴转动偏航角ψ得到Ox1y1z1，第二次绕Oz1转动俯仰角得到Ox2y2z2，第三次再绕Ox2轴转滚动角γ得到体轴系Oxbybzb，如图1所示，则从发射惯性系到体轴系的坐标转换矩阵为［3］：

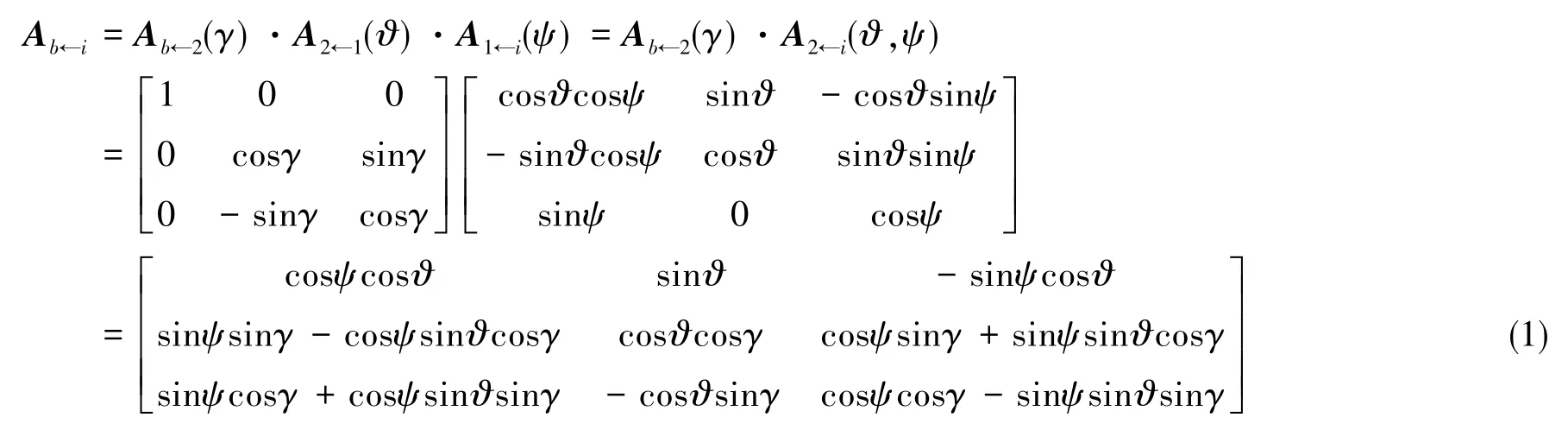
根据方向余弦矩阵与四元数的关系，得出：

合成转动的四元数：

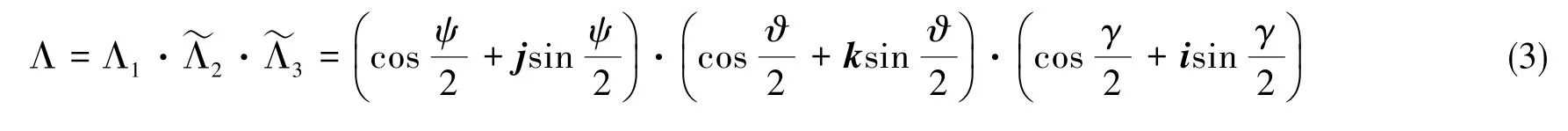
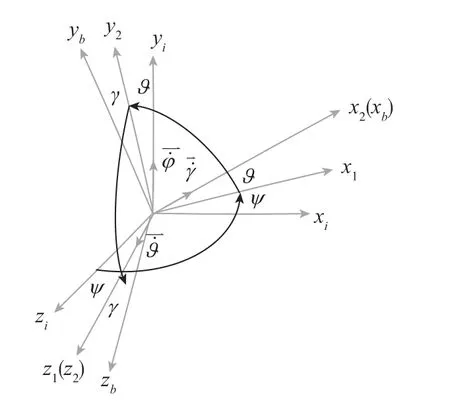
图1　从发射惯性系Oxiyizi到体轴坐标系Oxbybzb转换关系示意图Fig.1 Schematic diagram of the transformation from the inertial frame Oxiyizito the shaft system Oxbybzb

根据式（1）和式（2）求出：

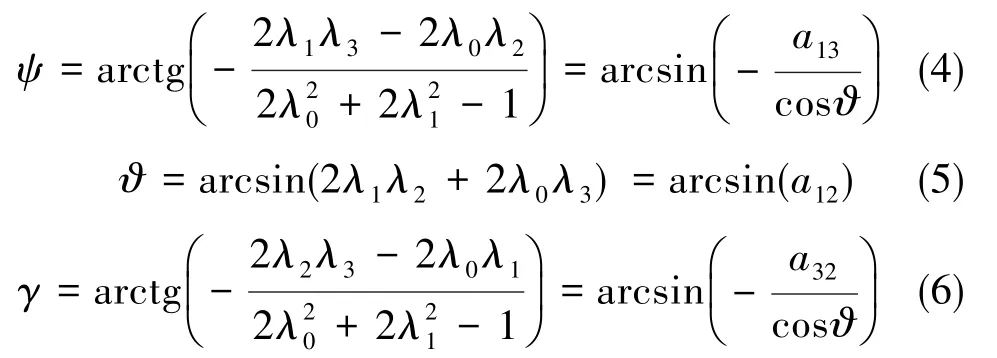
由速率陀螺测得飞行器角速度，据此可求解方向余弦矩阵微分方程和四元数微分方程［3］。

方向余弦矩阵是正交阵，根据这一性质可以对计算出的矩阵进行正交规范化，以减少数值积分误差的积累。对四元数微分方程的求解结果也要进行规范化。

从式（4）～式（6）可以看出，计算姿态角时仅使用了方向余弦矩阵中的3个元素。从普通的测量理论可知，在进行有独立随机误差的多次直接测量时，使用N次测量得出的均值，能使估值误差的方差减少到原来的1/N。因此，利用平均效应，尽可能多地使用方向余弦矩阵中的元素，就可以提高在随机误差条件下由方向余弦矩阵求取姿态角的精度。

2 基于改进牛顿法的计算姿态角的算法

把时刻ti的方向余弦矩阵的9个元素排成维数为np=9的矢量y(ti)=yi，该矢量的元素与3个姿态角有关。一般情况下，对于任意时刻，得出方程：

其中，

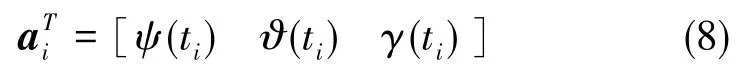
这里，f（yi，ai）是九维的已知的九维矢量变量yi和三维矢量ai的函数。所能知道的是矢量变量yi的观测值z（ti），它包含随机误差ξ（ti）=ξi。

那么，在式（7）的基础上形成观测模型：

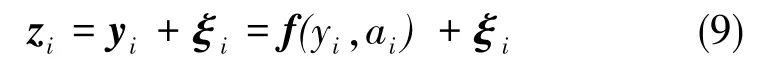
式中，ξi是随机误差，它是独立的标准的随机向量序列，其数学期望为0，协方差阵是R(ti)。

形成最小化泛函：

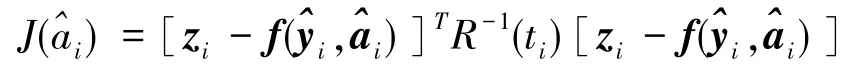
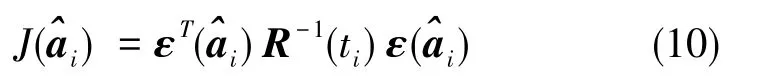
假设在所研究的情况中误差是独立的，那么协方差阵是对角阵，进一步假设观测是等精度的，于是就可以把协方差阵取为单位阵R（ti）=I。这样，式（10）就变成误差的平方和，有：

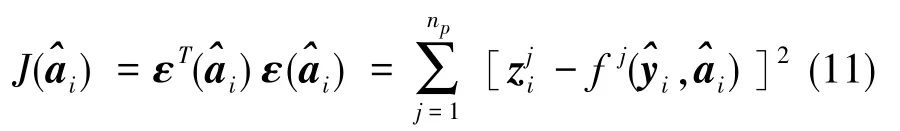
为了求出估值，使用改进的牛顿法［4］，递推公式为：

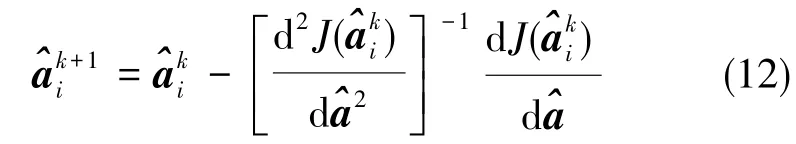
对（11）式求导数，得出：

计算二次导数：

式中，第一项与误差成比例，可以认为在极值附近它小到可以忽略。

对于每个ti时刻计算欧拉角，使用式（12）～式（14）式进行迭代计算，当矢量ak的模的增量小于某个预先给定的该模值的一个较小的比例数ε时，迭代过程结束。例如，可以取ε=0．01，有：

当满足式（15）时，迭代过程结束，这时的矢量ak+1的3个分量就看作是所求的姿态角的精确值。

这种方法的优点是最终结果与方向余弦矩阵的所有元素有关，并且在均方意义下是最优的，但是，迭代过程的收敛与起始近似值的选取及函数的拓扑性质有关，所以在飞行控制过程中需要实时计算姿态角时采用这种递推算法不方便。

3 提高计算姿态角精度的代数公式

3.1 由方向余弦矩阵的元素确定姿态角的公式

由于方向余弦矩阵微分方程求解过程中积分误差的积累，式（4）～式（6）计算姿态角过程中正弦与余弦的反三角函数的自变量的值可能超出其定义域，即超出［-1，1］的范围。如果根据单位矢量的标量积来确定姿态角，就可以回避上述缺点。除此之外，还要附加上使得出的姿态角位于合理值范围内的条件。总之，多使用方向余弦矩阵中的元素，既能提高精度，又可以使计算过程不发散且得出的角度值合理。

（1）计算俯仰角

体轴坐标系Oxb轴上的单位矢量ib在Oxizi平面内的分量在发射惯性系Oxiyizi内的投影是（a11，0，a13），按下面的公式计算俯仰角

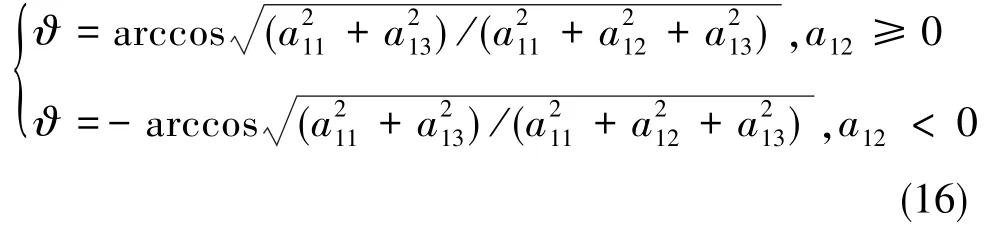
计算单位矢量ib与发射惯性系Oyi轴的标量积，就可以求出确定俯仰角的另一个公式：

该公式直接给出俯仰角的值，不需要附加条件。

（2）计算偏航角

根据图1中的几何关系，得出计算偏航角的公式：

（3）计算滚动角

根据两矢量的点乘公式，从图1中可以看出，可以用Oyb与Oy2轴上单位矢量iyb和iy2、Ozb轴Oz2轴上单位矢量izb和iz2的标量积求出滚动角γ。

由式（1）知，Oyb轴与Oy2轴上单位矢量在发射惯性系Oxiyizi内的投影分别是（a21，a22，a23）、根据前面求出的姿态角的三角函数与方向余弦矩阵的元素之间的关系，由式（16）～式（18）得出：

Ozb轴与Oz2轴上单位矢量在发射惯性系Oxiyizi内的投影分别是（a31，a32，a33）、（sinψ，0，cosψ），得出：

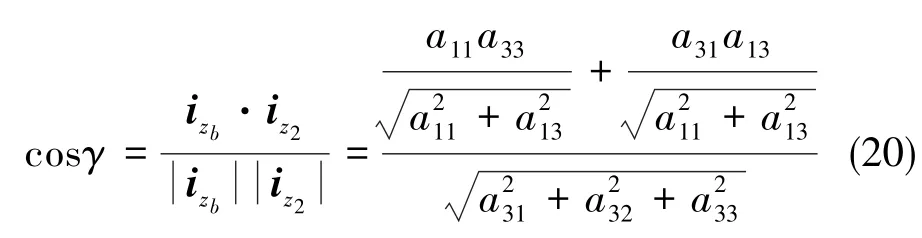
据此可得出滚动角γ，具体计算时还要考虑滚动角的范围再进一步细化。

3.2 由四元数的分量计算姿态角

在根据四元数计算姿态角的式（4）～式（6）中，已经包含了四元数的4个分量，即已经运用了求均值效应，但还存在精度更高的计算姿态角的公式。引入符号：

可以推导出：

从式（21）可以求出：

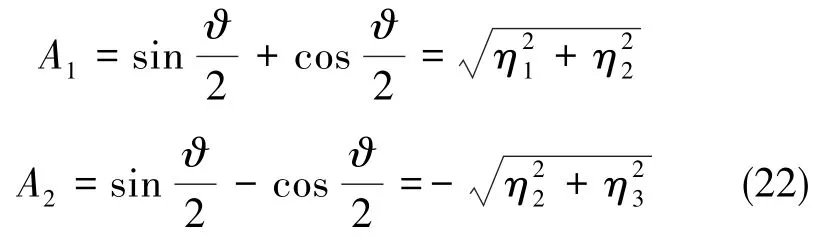
根据式（22），得出求姿态角的公式：

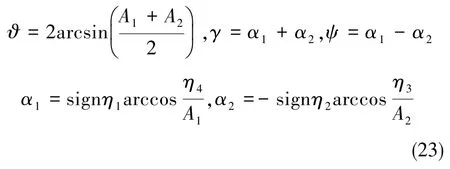
3.3 仿真验证结果

文献［4］以某型教练机在与铅垂面夹角为0．5°～2°的平面内做“斜筋斗”为例，验证所介绍方法的有效性。仿真结果表明，在俯仰角为ϑ∈（89°，89．5°）时，姿态角形式的微分方程已经发散；当俯仰角为ϑ∈（60°，70°）时，方向余弦和四元数形式的微分方程的积分结果开始出现误差；当俯仰角接近90°时，误差达到最大，通过正交规范化，可使微分方程求解精度提高。

根据方向余弦微分方程的积分结果按式（4）～式（6）求偏航角、俯仰角、滚动角时，随着俯仰角从0°逐渐增加到89．5°，俯仰角的计算误差从百分之几度增加到1°～1．5°，偏航角的误差逐渐增大直到出现振荡式特征，滚动角的误差已接近90°。而采用式（16）时，俯仰角误差只有0．01°～0．02°；采用式（18）计算偏航角时，误差最大为1．9°；采用式（19）计算滚动角时，误差最大为2．0°；根据四元数微分方程的积分结果求出方向余弦矩阵的元素然后再采用式（16）时，误差在0．04°左右。

4 结论

本文在比较分析计算飞行器姿态角各种方法的基础上，介绍了基于改进牛顿法的计算姿态角的算法。基于多次测量均值效应原理，介绍推导了根据刚体转动的方向余弦矩阵形式、四元数形式微分方程的数值积分结果，尽量多使用这两种方法中的元素，确定姿态角的方法。对于方向余弦矩阵的情况，本文介绍方法的效果更明显。

［1］陆元九．惯性器件［M］．北京：中国宇航出版社，1990．LUYuan⁃jiu．Inertialdevice［M］．Beijing：China Aerospace Press，1990．

［2］秦永元．惯性导航［M］．北京：科学出版社，2006．QIN Yong⁃yuan．Inertial navigation［M］．Beijing：Science Press，2006．

［3］范奎武．用四元数描述飞行器姿态时的几个基本问题［J］．航天控制，2012，30（4）：49⁃53．FAN Kui⁃wu．The key problems of describing rigid⁃body attitude by using quaternion［J］．Aerospace Control，2012，30（4）：49⁃53．

［4］В．В．Булгаков，О．Н．Корсун．Алгоритмы повышения точностирасчётаугловориентациилетательного аппарата［J］．Tеория и Cистемы Yправления，2016（1）：159⁃170．

The Research on Method for ImProving Calculating Precision of Attitude Angle in Flight Vehicle

FAN Kui⁃wu1，ZHANG Bing2
（1．Representatives Office of Navy of CALT，Beijing 100076；2．Beijing Aerospace Automatic Control Institute，Beijing 100854）

The deficiencies of the algorithm method for attitude angle in flight vehicle are analyzed in this paper．In this algorithm method，the attitude angle of flight vehicle is calculated by integral value of rotation＆motion differential e⁃quation，through the calculating of direction cosine and quaternion．Then the improved Newton method for attitude angle in flight vehicle is introduced as well．According to the mean value effect of multi⁃measurements，the algorithm method for im⁃proving attitude angle calculating⁃precision in flight vehicle by using maximumly the above two methods is de⁃duced．Simulation result shows the good effect of this method．

flight vehicle；attitude angle；quaternion；direction cosine；precision

U666．1

A

1674⁃5558（2016）01⁃01330

10．3969／j．issn．1674⁃5558．2016．06．007

2016⁃10⁃18

范奎武，男，博士后，研究方向为飞行器总体设计及导航、制导与控制。