PdSin（n＝1～15）团簇电子结构与光谱性质的理论研究

张　宇，王　翀，张　帅，李根全

（南阳师范学院物理与电子工程学院，南阳473061）

PdSin（n＝1～15）团簇电子结构与光谱性质的理论研究

张宇，王翀，张帅，李根全

（南阳师范学院物理与电子工程学院，南阳473061）

在卡里普索（CALYPSO）结构预测的基础上，采用密度泛函理论（DFT）B3LYP方法，优化得到PdSin（n＝1～15）团簇的基态结构，对其电子性质、红外光谱和拉曼光谱进行了讨论.结果表明，PdSin（n＝1～15）团簇的基态构型随n值的增大由平面结构向立体结构演化；当n≤4时，PdSin团簇的红外与拉曼活性在450～500 cm－1范围内表现较好，当n≥5时，PdSin团簇的红外与拉曼活性在50～500 cm－1范围内表现较好.

PdSin团簇；密度泛函理论；几何结构；电子性质；光谱学

由于过渡金属（Transition Metal，TM）原子掺杂硅团簇具有结构多样性并趋向构建闭壳电子结构的特性，在最近几十年备受关注.TMSin团簇具有与纯Sin团簇不同的物理化学性质，有助于合成新型硅基半导体材料，在微电子与材料科学方面应用广泛.Ohara等［1］采用质谱法和光电子能谱法研究了过渡金属Ti，Hf，Mo和W掺杂Si团簇的几何和电子结构，发现当n≥15时过渡金属Ti，Hf，Mo开始嵌入Si笼；Koyasu等［2］利用质谱分析、阴离子光电扫描和对H2O的吸附反应等方法研究了过渡金属Sc， Y，Lu，Ti，Zr，Hf，V，Nb，Ta掺杂Si团簇的结构和电子性质，因为和形成了闭壳电子结构和笼形几何结构，因而更加稳定且易于生成；Miyazaki等［3］对过渡金属W， Re，Ta，Nb掺杂Sin团簇（n＝12，14，16）进行了密度泛函理论研究，计算了其化学势和化学硬度，结果表明，掺杂提高了纯Si团簇的化学活性；Ren等［4］研究了RhSin（n＝1～6）团簇，发现RhSin的基态构型与Sin＋1构型基本一致.

钯（Pd）作为一种重要的过渡金属元素，对氢具有很好的亲和力，具有渗氢并使其纯化的特征，是工业生产中重要的催化材料，已广泛应用于各种化学反应，如氢化、脱氢反应、石油和汽车尾气的裂解等［5，6］.最新研究发现Pd纳米粒子具有铁磁性，可用于磁存储材料［7］.然而，关于PdSin团簇的研究报道很少，仅有孙建敏等［8］利用相对论密度泛函理论研究了PdSin团簇的几何结构与电磁性质，并进行了Y，Pd，La，Yb，Lu掺杂Si团簇之间的比较，但未讨论PdSin基态结构的演变规律及光谱性质.本文在卡里普索（CALYPSO）结构预测的基础上，对PdSin（n＝1～15）团簇的预测构型进行优化计算，确定了最低能量结构，分析了PdSin团簇的基态构型变化规律、电子和光谱性质，以期为硅基半导体材料的研究设计提供可靠的理论依据.

1 计算方法

CALYPSO是基于粒子群优化算法（Particle swarm optimization）的一种结构预测方法，该方法可以在只了解结构化学组分的情况下，采用随机结构产生、相似结构判断及结构演化等一系列技术手段预测研究体系的稳态结构，在团簇结构的预测研究方面应用广泛［9～11］.本文首先使用CALYPSO对PdSin（n＝2～15）团簇的可能结构进行了几何搜索，使用点群对称性限制随机产生的第一代初始结构，然后采用局域结构优化和粒子群优化操作产生预测结构.PdSin（n＝2～15）团簇中不同n值约对应20种预测结构，同时考虑约10种随机结构也作为预测结构.在预测出的结构基础上使用Gaussian 09程序包［12］，采用杂化泛函B3LYP对获得的预测结构进行了进一步的优化与频率计算.计算中能量收敛精度优于10－6a.u，未限制结构的对称性，同时考虑不同的自旋多重态（1，3，5），将得到频率为正的最低能量结构作为基态团簇.考虑到Pd是重金属元素，相对论效应和电子相关效应明显，故对Pd原子采用包含相对论效应的有效核势（ECP）基组LanL2DZ以降低运算量，对Si原子采用全电子6⁃311＋G（d）基组，因此本文采用混合基组GENECP［对Pd和Si分别采用LANL2DZ和6⁃311＋G（d）基组］进行计算.为了确保所选择计算方法的可靠性，使用相同条件计算了二聚体Si2和Pd2的键长、振动频率与PdSi的电离势，得到的结果分别为0.2167 nm，540.37 cm－1；0.2512 nm，205.3 cm－1和7.53 eV，与实验结果［0.2246 nm，510.98 cm－1［13］；0.248 nm，（210±10）cm－1［14，15］；（8.4±0.5）eV［16］］基本一致.此外，计算得到PdSi的键长（0.213 nm）、振动频率（465.89 cm－1）与Wu等［17］计算得到的结果（0.212 nm，473 cm－1）很接近.表明本文选用的计算方法对于PdSin团簇是适用的.

2 结果与讨论

2.1 团簇的几何结构

采用上述方法计算得到PdSin（n＝1～15）团簇的多个稳定结构，为方便讨论，仅给出团簇的基态结构，其构型随团簇尺寸依次命名为na，n代表Si原子的个数.具体结构如图1所示.

Fig．1 Lowest energy structures of PdSin（n＝1—15）clusters

对于PdSi二聚体，基态为自旋单重态1Σ，具有C∞v对称性，Pd—Si键键长为0.21 nm，平均结合能为2.43 eV.PdSi2的基态为自旋三重态3B1，具有C2v对称性的等腰三角形，Si—Pd键长为0.23 nm（腰），Si—Si键长为0.28 nm（底边），可看作由一个Si原子戴帽于PdSi二聚体而生成.从n＝3开始，除n＝12，15外，PdSin团簇的基态均为自旋单重态，最低能量构型开始由平面结构转变为立体结构. PdSi3的最稳定构型为立体蝶形（Cs，1A′），可看作是在PdSi2的基态结构上戴帽一个Si原子而得到.一个Pd原子戴帽于3a结构可得到畸变的四角锥4a，对称性为Cs，电子态为1A′.PdSi5的基态结构5a可看作是在4a的基态结构上戴帽一个Pd原子得到，对称性为C1.PdSi6的基态结构6a为对称性为C1的三角双锥，Pd为双锥的一个顶点，另一个Si原子戴帽在对面的锥面上.PdSi7的基态结构7a是在对称性为Cs的Si类船型结构上戴帽一个Pd原子得到.PdSi8的最低能量结构8a具有C1对称性，可看作在基态结构7a的基础上带帽一个Si原子得到. PdSi9的最稳定构型9a为具有C1对称性的变形五棱柱，电子态为1A.PdSi10的基态结构10a为9a构型戴帽一个Si原子，对称性为C1，电子态为1A.从n＝11开始，Pd原子的位置从团簇表面陷入到Si笼内部，团簇结构出现较大变化；PdSi11的基态结构11a可看作是一个不规则的五棱柱戴帽一个Si原子，而Pd原子处于五棱柱的中心，对称性为C1，电子态为1A；图2给出了所有基态结构11a的Pd—Si键键长，平均键长为0.26 nm，内笼直径约为0.49 nm.PdSi12的基态结构12a是一个六棱柱，Pd原子处于六棱柱中心.PdSi13的基态结构13a为自旋单重态C1，可看作是基态结构12a戴帽一个Si原子构成.PdSi14和PdSi15的基态结构均为C1对称性，Pd原子处于Si笼中心的结构.

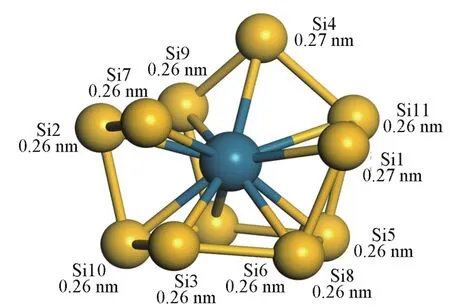
Fig．2 Lowest energy structures and bond length of each Pd—Si of PdSi11

综上，Pd原子掺杂进纯Si团簇后，随着Si原子数目不断增多，位置由戴帽的顶点移动到团簇表面，基态结构相应地从平面结构转化为立体结构，当n≥11时，Pd完全陷入Si笼中心，演化过程与过渡金属团簇TMSin（TM＝Ti，Zr，Hf；n＝8～16）［18］类似，形成笼形结构所需Si原子数量不同可能与过渡金属原子的半径有关；PdSin团簇基态构型基本上是在PdSin－1构型上戴帽一个Pd原子或Si原子形成.

2.2 团簇的稳定性

为分析研究PdSin（n＝1～15）团簇的稳定性，计算了PdSin团簇最低能量结构的结合能（Eb）、二阶能量差分（Δ2E）、离解能（D）与能隙（Egap）：

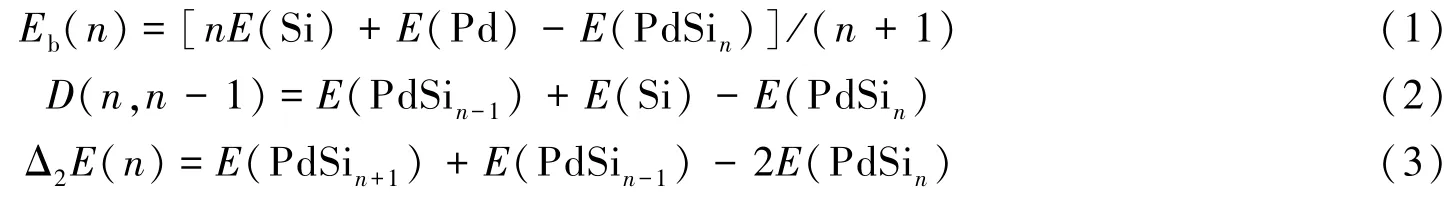
式中：E（Si）和E（Pd）分别为Si和Pd的单原子基态的总能量；能量E（Sin），E（PdSin），E（PdSin－1）与E（PdSin＋1）分别为对应团簇基态的总能量.

图3给出PdSin团簇的Eb，Δ2E，D与Egap随团簇尺寸变化的趋势.由图3（A）可见，PdSin团簇的Eb随n值的增大而增加，当n＝1～4时，PdSin团簇的Eb增幅迅速；当n＝5～7时，Eb增大速度有所减缓；当n≥8时，Eb的增加趋于平稳，变化不大，说明随着Si原子的增加，n值变化对团簇的性质影响趋于缓和.与Sin＋1团簇的结合能相比，掺杂团簇的Eb均大于Sin＋1团簇［19］，二者之差在n＝12处达到最大值，约为0.52 eV，说明过渡金属元素Pd的掺入增强了纯Si团簇的稳定性，这与CoSin和NiSin团簇的表现一致［20，21］.

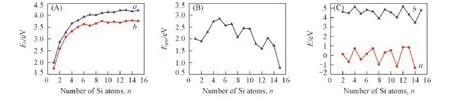
Fig．3 Size dependence of the averaged binding energy（Eb）of PbSin（n＝1—15）（a）and Sin＋1（b）（A），HOMO⁃LUMO energy gap（Egap，B），second⁃order energy difference（Δ2E，a）and fragmentation energy（D，b）of the lowest energy structures of PdSin（n＝1—15）clusters（C）

电子从最高占据轨道（HOMO）向最低未占据轨道（LUMO）跃迁的能力表现为能隙，值越大则电子跃迁越困难，因而能隙常用来分析团簇的稳定性［22］.图3（B）显示PdSin团簇随尺寸n的增加能隙Egap出现明显的振荡现象.当n＝5，7，9，13时，Egap出现峰值，说明相应尺寸PdSin团簇的化学稳定性比邻近团簇高，相对而言难于进行化学反应.

由团簇物理学可知，团簇的稳定性与Δ2E和D关系密切，Δ2E值越大，D越大，则团簇越稳定.从图3（C）可见，D和Δ2E随团簇尺寸n变化的规律基本一致，均呈现波动变化趋势.当n＝4，7，10，12时，Δ2E出现峰值，这说明对应尺寸PdSin团簇相对较稳定；当n＝4，6，9，12时，D出现峰值，表明对应尺寸PdSin团簇较为稳定.综上，PdSi4与PdSi12具有较高的D和Δ2E，稳定性较强.

2.3 团簇的电荷转移

表1列出了PdSin基态团簇的自然布居（Natural population）及自然电子构型（Natural electron confi⁃guration）数据.由表1可见，Pd原子的4d轨道失去0.39～0.54 e，5s轨道和5p轨道分别得到0.35～0.95和0.02～2.0 e，且当n≥11时，电荷的转移数量急剧增加，这可能是电荷在陷入Si笼中心的Pd原子与周围的Si原子之间进行了充分的转移而导致的.进一步分析可得，团簇中电荷主要是从Pd原子的4d轨道和Si原子的3s轨道向Pd原子的5s和5p轨道转移，在Pd⁃Si原子间发生了混合的spd杂化.这种原子间产生的相互作用提高了PdSin团簇的稳定性，与Eb的分析完全一致.

Table 1 Natural charge population（NCP）and natural electron configuration（NEC）of Pd atom and Si atoms in the lowest⁃energy PdSin（n＝1—15）clusters

2.4 团簇的红外光谱与拉曼光谱

分子振动光谱包括红外光谱和拉曼光谱，团簇内部原子间相对振动产生的偶极矩变化反映为红外光谱，在相应波数处产生吸收峰，且变化越大产生的红外吸收峰越强；而由于原子的相对振动引起的团簇极化率变化反映为拉曼光谱［23～25］.

图4给出了PdSin（n＝2～6）团簇的红外光谱及拉曼光谱.可见，PdSi2团簇的红外光谱和拉曼光谱均有2个较强峰，最强峰都位于477.03 cm－1处，振动模式为Si1和Si2原子的伸缩振动.红外光谱次强峰位于282.01 cm－1处，振动模式为Si1和Si2原子的伸缩振动和Pd原子垂直于Si1—Si2轴线的上下运动；拉曼光谱次强峰位于247.04 cm－1处，振动模式为Pd—Si1和Pd—Si2的伸缩振动.PdSi3团簇的红外光谱峰值位于470.30 cm－1处，振动模式为Si原子之间的摇摆振动；拉曼光谱有3个强振动峰，分别位于481.48，169.54和100.59 cm－1处，对应的振动模式为3个Si原子的呼吸振动、Pd—Si3的伸缩振动和Si1—Si2之间的伸缩振动.PdSi4团簇的2个较强的红外振动峰位于波数472.05和307.86 cm－1处，振动模式为Pd—Si2的摇摆振动和Pd—Si3的伸缩振动；拉曼光谱的强振动峰位于450.46 cm－1处，为Si与Pd原子之间的呼吸振动.PdSi5团簇的红外光谱和拉曼光谱有多个较强峰分布在135～450 cm－1范围内，最强峰位于380.45 cm－1处，振动模式为Si1—Si3绕Pd—Si4轴线的摇摆振动；拉曼光谱也有多个峰值，445.40 cm－1处的强振动峰模式为Si原子的呼吸振动.PdSi6团簇的红外光谱和拉曼光谱在135～470 cm－1范围内有多个峰值分布，振动模式主要为Si原子之间的伸缩振动和呼吸振动.

Fig．4 Infrared（A—E）and Raman spectra（A1—E1）of PdSin（n＝2—6）clusters（A，A1）PdSi2；（B，B1）PdSi3；（C，C1）PdSi4；（D，D1）PdSi5；（E，E1）PdSi6.

图5给出了PdSin（n＝7～11）团簇的红外光谱及拉曼光谱.由图5可见，PdSi7团簇的最强峰位于462.31 cm－1处，振动模式主要为Si2，Si3和Pd原子之间的呼吸振动；位于339.04 cm－1处的拉曼光谱最强峰和位于400.21 cm－1处的次强峰振动模式主要是Si原子间的呼吸振动.PdSi8团簇的红外光谱最强峰位于498.20 cm－1处，振动模式是Si原子之间的摇摆振动；拉曼光谱有多个振动峰值，对应的振动模式为Si原子之间的呼吸振动和Pd—Si，Si—Si之间的伸缩振动.PdSi9团簇最强的红外振动峰位于438.87 cm－1处，振动模式为Si1，Si2，Si4，Si8之间的呼吸振动和Si5，Si6，Si7，Si9的伸缩振动；拉曼光谱中有2个强振动峰，400.94 cm－1处振动模式为Si原子之间的呼吸振动，347.29 cm－1处振动模式为Pd—Si和Si—Si之间的伸缩振动.PdSi10团簇的红外光谱有多个较强峰，最强峰位于408.20 cm－1处，振动模式是Si原子之间的伸缩振动；拉曼光谱最强振动峰位于311.36 cm－1处，对应的振动模式是Si原子之间的呼吸振动.PdSi11团簇的红外光谱最强峰位于202.77 cm－1处，次强峰位于222.15 cm－1处，振动模式都是Si原子和Pd原子的伸缩振动；拉曼光谱最强峰位于361.54 cm－1处，振动模式也是Si原子和Pd原子的伸缩振动.

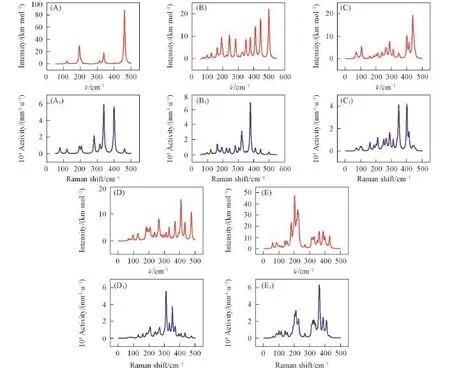
Fig．5 Infrared（A—E）and Raman spectra（A1—E1）of PdSin（n＝7—11）clusters（A，A1）PdSi7；（B，B1）PdSi8；（C，C1）PdSi9；（D，D1）PdSi10；（E，E1）PdSi11.

Fig．6 Infrared（A—D）and Raman spectra（A1—D1）of PdSin（n＝12—15）clusters（A，A1）PdSi12；（B，B1）PdSi13；（C，C1）PdSi14；（D，D1）PdSi15.

图6给出了PdSin（n＝12～15）团簇的红外光谱及拉曼光谱.可见，PdSi12团簇的红外光谱中有3个较强的振动峰，最强峰位于223.63 cm－1处，振动模式为Si的摇摆振动；次强峰位于217.91 cm－1处，振动模式为Si原子间的呼吸振动；第3强峰位于375.66 cm－1处，振动模式为Si原子之间的伸缩振动；拉曼光谱有4个强振动峰，最强峰和次强峰分别位于391.53和297.21 cm－1处，振动模式是Si原子以Pd原子为中心的呼吸振动；第3强峰位于147.70 cm－1处，振动模式为Si5—Si12，Si7—Si11原子之间的摇摆振动；第4强峰位于236.72 cm－1处，振动模式为Si5—Si12和Si7—Si11原子之间的伸缩振动，其它强峰的拉曼活性与最强峰非常接近.PdSi13团簇的红外光谱最强峰位于205.84 cm－1处，次强峰位于381.11 cm－1处，第3强峰位于433.00 cm－1处，振动模式主要为Si原子的摇摆振动，其它强峰的光谱强度与最强峰非常近似；拉曼光谱在整个频率范围存在多个峰值，振动模式多为Si原子的伸缩振动.PdSi14团簇的红外光谱峰值较多，振动模式主要为Si原子的伸缩振动；拉曼光谱最强峰位于299.54 cm－1处，对应的振动模式为Si原子关于Pd的呼吸振动.PdSi15团簇的红外光谱最强峰位于102.95 cm－1处，振动模式为Si原子之间的摇摆振动；拉曼光谱最强振动峰位于299.70 cm－1处，对应的振动模式为Si原子之间的伸缩振动.

综上可见，当n≤4时，PdSin团簇的红外活性与拉曼活性在450～500 cm－1范围内表现较好，在其它频段峰值较少.当n≥5时，PdSin团簇的红外活性与拉曼活性在50～500 cm－1范围内均有峰值分布，因而在整个频段内都表现得较好.当n＝5，6时，Sin＋1团簇红外光谱实验值各具有一个峰值［26］，与PdSin团簇有很大不同；当n＝9时，Sin＋1团簇［26］与PdSin团簇红外光谱分布范围类似，但峰值位置有所不同.当n＝1～15时，SinY－团簇红外光谱和拉曼光谱理论计算值［27］与PdSin团簇分布范围近似，但峰值个数和所在波数不一致.PdSin团簇红外光谱最强峰的振动主要为摇摆和伸缩振动，出现几率较平均，拉曼光谱最强振动峰大部分为Si原子的呼吸振动，这可能是因为Si⁃Pd原子之间产生了较强的相互作用，PdSin团簇的偶极矩和极化率产生了较大变化的结果；当n值不同时，红外活性变化范围较大，这是由于不同的振动模式对原子的电荷分布造成的影响不同，使偶极矩的变化不同所导致；当n＝12时，PdSi12产生了多个较强的振动峰，可能是PdSi12具有较强的稳定性.

3 结 论

采用CALYPSO结构预测方法和密度泛函理论（DFT）在B3LYP水平上研究了PdSin（n＝1～15）团簇的几何结构、稳定性和光谱性质.结果表明，当n＝1，2时，PdSin团簇基态构型为平面结构；当n≥3时，立体结构的基态构型开始形成；当n≥11时，Pd陷入Sin中心，形成笼状结构.PdSin团簇基态构型可认为是在PdSin－1构型基础上戴帽形成的；在PdSin团簇中，原子间的成键相互作用随n值的增大而增强，电子结构随Si原子的增加越来越稳定，结构也更加紧凑，当n≤4时，PdSin团簇的红外活性与拉曼活性在450～500 cm－1范围内表现较好，在其它频段峰值较少；当n≥5时，PdSin团簇的红外活性与拉曼活性在50～500 cm－1范围内均有峰值分布，在整个频段内表现较好，拉曼光谱最强峰的振动大部分为Si原子的呼吸振动.

［1］ Ohara M.，Koyasu K.，Nakajima A.，Kaya K.，Chem．Phys．Lett．，2003，371（3），490—497

［2］ Koyasu K.，Atobe J.，Akutsu M.，Mitsui M.，Nakajima A.，J．Phys．Chem．A，2007，111（1），42—49

［3］ Miyazaki T.，Hiura H.，Kanayama T.，Eur．Phys．J．D，2003，24（1），241—244

［4］ Ren Z.Y.，Hou R.，Guo P.，Gao J.K.，Du G.H.，Wen Z.Y.，Chin．Phys．B，2008，17（6），2116—2123

［5］ Ni M.，Zeng Z.，J．Mol．Struct．：Theochem．，2009，910（1），14—19

［6］ Li J.N.，Pu M.，Ma C.C.，Tian Y.，He J.，Evans D.G.，J．Mol．Catal A：Chem．，2012，359，14—20

［7］ Douglass D.C.，Bucher J.P.，Bloomfield L.A.，Phys．Rev．B，1992，45（11），6341—6344

［8］ Sun J.M.，Zhao G.F.，Bai Y.Z.，Wang Y.X.，J．At．Mol．Phys．，2012，29（1），67—75（孙建敏，赵高峰，白燕枝，王渊旭.原子与分子物理学报，2012，29（1），67—75）

［9］ Wang Y.，Lv J.，Zhu L.，Ma Y.，Phys．Rev．B，2010，82（9），7174—7182

［10］ Wang Y.，Lv J.，Zhu L.，Ma Y.，Comput．Phys．Commun．，2012，183（10），2063—2070

［11］ Wang Y.，Miao M.S.，Lv J.，Zhu L.，Yin K.，Liu H.，Ma Y.，J．Chem．Phys．，2012，137（22），3896—3903

［12］ Frisch M.J.，Trucks G.W.，Schlegel H.B.，Scuseria G.E.，Robb M.A.，Cheeseman J.R.，Zakrzewski V.G.，Montgomery J.A.，Strat⁃mann R.E.，Burant J.C.，Dapprich S.，Millam J.M.，Daniels A.D.，Kudin K.N.，Strain M.C.，Farkas O.，Tomasi J.，Baron V.，Cos⁃si M.，Cammi R.，Mennucci B.，Pomelli C.，Adamo C.，Clifford S.，Ochterski J.，Petersson G.A.，Ayala P.Y.，Cui Q.，Morokuma K.，Malick D.K.，Rabuck A.D.，Raghava⁃chari K.，Foresman J.B.，Cioslowski J.，Ortiz J.V.，Stefanov B.B.，Liu G.，Liashenko A.，Piskorz P.，Komaromi I.，Gomperts R.，Martin R.L.，Fox D.J.，Keith T.，Al⁃Laham M.A.，Peng C.Y.，Nanayakkara A.，Gonzalez G.，Challacombe M.，Gill P.M.W.，Johnson B.，Chen W.，Wong M.W.，Andres J.L.，Gonzalez C.，HeadGordon M.，Replogle E.S.，Pople J.A.，Gaussian 09，Revision C．01，Gaussian Inc.，Wallingford CT，2009

［13］ Huber K.P.，Herzberg G.，Van N.Y.，Nostrand／Reinhold，1979，212—214

［14］ Ho J.，Ervin K.M.，Polak M.L.，Gilles M.K.，Lineberger W.C.，J．Chem．Phys．，1991，95（7），4845—4853

［15］ Ho J.，Polak M.L.，Ervin K.M.，Lineberger W.C.，J．Chem．Phys．，1993，99（11），8542—8551

［16］ Auwera⁃Mahieu A.V.，Peeters R.，Mcintyre N.S.，Drowart J.，Trans．Faraday Soc．，1970，66，809—816

［17］ Wu Z.J.，Su Z.M.，J．Chem．Phys．，2006，124（18），471—484

［18］ Hossain D.，Pittman C.U.，Gwaltney S.R.，Chem．Phys．Lett．，2008，451（1），93—97

［19］ Qin W.，Lu W.C.，Zhao L.Z.，Zang Q.J.，Wang C.Z.，Ho K.M.，J．Phys．Condens．Matter．，2009，21（45），1484—1489

［20］ Wang J.，Zhao J.，Ma L.，Wang B.，Wang G.，Phys．Lett．A，2007，367（4），335—344

［21］ Li J.R.，Yao C.H.，Mu Y.W.，Wan J.G.，Han M.，J．Mol．Struct．：Theochem．，2009，916（1），139—146

［22］ Xia X.X.，Hermann A.，Kuang X.Y.，Jin Y.Y.，Lu C.，Xing X.D.，J．Phys．Chem．C，2015，120（1），677—684

［23］ Gong J.，Cao H.Y.，Li S.M.，Tang Q.，Yang Y.J.，Zheng X.F.，Chem．J．Chinese Universities，2014，35（6），1267—1276（宫健，曹洪玉，李慎敏，唐乾，杨彦杰，郑学仿.高等学校化学学报，2014，35（6），1267—1276）

［24］ Jin Y.，Maroulis G.，Kuang X.Y.，Ding L.P.，Lu C.，Wang J.J.，Lv J.，Zhang C.Z.，Ju M.，Phys．Chem．Chem．Phys.，2015，17（20），13590—13597

［25］ Ding L.P.，Zhang F.H.，Zhu Y.S.，Lu C.，Kuang X.Y.，Lv J.，Shao P.，Sci．Rep．，2015，5，15951

［26］ Fielicke A.，Lyon J.T.，Haertelt M.，Meijer G.，Claes P.，Haeck J.D.，Lievens P.，J．Chem．Phys．，2009，131（17），2891—2899

［27］ Jaiswal S.，Babar V.P.，Kumar V.，Phys．Rev．，2013，88（8），2639—2648

（Ed.：Y，Z，S）

†Supported by the National Natural Science Foundation of China（No.11304167），the Postdoctoral Science Foundation of China（Nos. 20110491317，2014T70280）and the Program for Science＆Technology Innovation Talents in Universities of Henan Province，China（No. 15HASTIT020）.

Density Functional Theory Study of the Structural and Spectrum Properties for PdSin（n＝1—15）Clusters†

ZHANG Yu，WANG Chong，ZHANG Shuai，LI Genquan∗
（Department of Physics＆Electronic Engineering，Nanyang Normal University，Nanyang 473061，China）

The possible geometrical structure of the PdSin（n＝1—15）clusters were optimized with density⁃functional theory（DFT）approach at B3LYP level，based on the crystal structure analysis by particle swarm optimization（CALYPSO）.The electronic properties，infrared and Raman spectrum were also studied.The cal⁃culated results indicate that the most stable structures of PdSinclusters develop from planar to three⁃dimen⁃sional structure；when n≤4，vibrational frequencies are in a range of 450—500 cm－1；when n≥5，vibrational frequencies are in a range of 50—500 cm－1，the strong peak modes are found almost to be an breathing vibra⁃tion of the Si atoms.

PdSincluster；Density functional theory；Geometrical structure；Electronic property；Spec⁃troscopy

O641

A

10.7503／cjcu20160349

2016⁃05⁃18.网络出版日期：2016⁃11⁃21.

国家自然科学基金（批准号：11304167）、中国博士后科学基金（批准号：20110491317，2014T70280）和河南省高校创新人才支持计划项目（批准号：15HASTIT020）资助.

联系人简介：李根全，男，博士，教授，主要从事团簇电子结构研究.E⁃mail：nynulgq＠21cn.com