利用近场Gordon积分近似的矩量法-物理光学混合方法

孔蓓蓓 盛新庆

(北京理工大学信息与电子学院电磁仿真中心,北京 100081)



利用近场Gordon积分近似的矩量法-物理光学混合方法

孔蓓蓓 盛新庆

(北京理工大学信息与电子学院电磁仿真中心,北京 100081)

针对电大金属目标的电磁计算,提出了一种新的矩量法-物理光学(Method of Moment-Physical Optics,MoM-PO)混合方法,以解决传统的MoM-PO混合法中PO区域和MoM区域耦合项的计算时间过长问题.用Gordon积分计算目标的PO区域对MoM区域的作用,并加入近场近似处理.该方法避免了传统的MoM-PO混合法中耦合项积分方程的计算,加大PO区域的剖分面元的大小,能够有效地降低矩阵规模和未知数个数,因而降低了内存,减少了计算时间.数值算例结果表明,近场Gordon积分近似的MoM-PO混合方法能够有效地减少耦合项的计算时间,并能达到理想的精度.

MoM;PO;混合方法;Gordon积分

DOI 10.13443/j.cjors.2015110603

引 言

计算电大导体目标的电磁散射是计算电磁学中一个重要的和具有挑战性的问题[1].矩量法(Method of Moment,MoM)由于其精确性和高效性,成为计算电磁学的主要方法之一,在计算三维目标的散射问题上得到了广泛应用.用矩量法求解表面积分方程时,需要采用适当的基函数(如RWG(Rao-Wilton-Glisson)基函数[2])对等效源进行离散,为了达到理想的精度,对三维目标的剖分通常采用较小的网格.随着目标电尺寸的增大,矩量法的计算成本大大增加,无法满足计算需求.

物理光学(Physical Optics,PO)方法[3]非常适合求解电大问题,然而,对于目标中较为复杂和细小的部分,物理光学法不能准确地近似表面电流,为此通常采用与矩量法相结合的方法[4-9].尤其对于天线的辐射问题,MoM-PO混合法十分有效.此外,由于PO方法对于目标阴影区无法准确地近似,对曲率较小的电大目标的散射,也可以采用MoM-PO混合法.MoM-PO混合法将目标分为PO区域和MoM区域,PO区域的等效电流用PO电流近似,MoM区域的等效电流仍然采用离散积分方程、求解矩阵的方法进行计算.但是,还需要计算PO区域的电流对MoM区域的作用,而这部分仍然需要较长的时间[10],因为两个区域的基函数之间的耦合都需要进行计算.

为了减少耦合项的计算时间,本文提出了一种利用近场Gordon积分近似的MoM-PO混合方法.PO区域对MoM区域的作用直接通过求解PO电流在MoM区域的散射场得到,散射场的求解采用Gordon积分方法[11],同时加入近场近似[12]以减少近场散射场的相位误差.由于该方法不需要用基函数表示PO电流,对PO区域可以采用较大的面元进行剖分,计算耦合项时也不需要求积分方程,从而大大减少了耦合项的计算时间.

1 利用近场Gordon积分近似的MoM-PO方法

1.1 传统的MoM-PO混合法

对于一个平面波入射下的完美电导体(Perfect Electric Conductor,PEC)目标的散射问题,入射场用(Ei,Hi)来表示,以电场积分方程为例,可以建立如下方程[13]:

(1)

L算子定义为

(2)

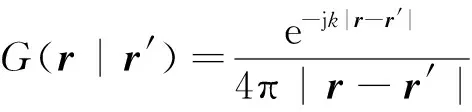
(3)

r代表场点位置,r′代表源点位置.

用RWG基函数对面积分方程(1)进行离散,gi为RWG矢量基函数,并采用伽辽金匹配,可得到下面的离散方程:

(4)

将式(4)简写为[Pij]{J}={bi},其中J为待求未知数.传统的MoM-PO混合法将积分区域分为两部分:PO区域和MoM区域.PO区域为目标的光照区,该区域的电流可以近似地表示为

(5)

NPO为PO区域未知数的个数．PO区域的J可由式(5)得到,从而,待求未知数仅为MoM区域的未知数,求解的离散方程为

(6)

(7)

1.2 利用近场Gordon积分近似的MoM-PO方法

MoM-PO混合法使未知数的个数和矩阵规模都得到了缩减,降低了内存并减少了计算时间.然而,随着计算目标的增大,PO区域与MoM区域的耦合项b′的计算时间也大大增加.由式(7)可以看出,b′的计算时间主要受PO区域离散未知数的个数NPO以及每一个离散位置对MoM区域的作用(即积分项PijJj)的计算时间影响.为了减少耦合项的计算时间,我们提出了利用Gordon积分和近场近似的MoM-PO混合方法.

(8)

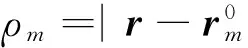
(9)

图1 三角面元的符号

耦合项b′为PO区域的等效电流JPO在MoM区域上的散射场与试函数的内积:

b′=∫gi·Esds.

(10)

与式(7)相比,式(10)不需要计算积分方程,从而不需要用基函数表示PO电流,对PO区域的剖分可以选择较大的面元,大大减少了计算时间.

另外,我们将多层快速多极子技术(Multilevel Fast Multipole Algorithm,MLFMA)应用于MoM中,加速对MoM区域矩阵填充和未知数的求解,对于计算电大尺寸的目标,可以节约计算时间.在接下来的数值算例中,混合法的MoM区域未知数的计算都采用MLFMA技术进行加速.

2 数值算例

在本节中,我们分别用MLFMA、传统混合法以及本文中提出的近场Gordon积分近似的混合方法计算了两个算例.根据入射场的入射方向,将目标的光照区作为PO区域,阴影区作为MoM区域.对于近场Gordon积分近似的混合方法,我们采用平均边长为0.5λ的三角面元对PO区域进行剖分,MoM区域的剖分大小为0.1λ,两个区域之间采用共形网格.MLFMA和传统混合法均采用边长为0.1λ的网格剖分.

首先计算了一个底面积为8λ×8λ,高为5λ的PEC立方体.平面波沿着-Z轴入射,VV极化下的双站RCS计算结果如图2所示.表1统计了不同方法计算的未知数个数以及耦合项的计算时间,为了比较两种混合法的计算精度,引入RCS的均方根误差:

(11)

式中:σM代表MLFMA的计算结果,作为精度比较的参考值;σH代表混合法的计算结果;N代表观察角度的个数.从仿真结果可以看出,近场Gordon积分近似的混合方法计算的RCS结果能够较为准确地描绘RCS的变化趋势,与传统的混合法相比,耦合项的计算时间大大减少,减少了约99%.这是由于在计算耦合项的过程中,我们的方法不需要计算积分方程,每个亮区面元的散射场可以由面元的顶点位置解析计算出来,从而节省了时间.加大亮区面元的剖分,可以大大减少亮区面元散射场计算个数,使耦合项计算时间减少.另外,由于两个区域之间采用共形网格,使得MoM区域的未知数个数有所下降.

(a) 模型

(b) 双站RCS图2 大小为8λ×8λ×5λ的立方体模型及其RCS仿真

未知数个数耦合项计算时间/sεRMS/dB近场Gordon近似混合法414531374.7393传统混合法77104150252.7498

由于本文所提方法不仅考虑了亮区电流的等效,还在计算耦合项时采用了远场散射场的计算方法,比起传统的用RWG将PO电流用基函数表示的方法误差有所增大,对于图2中的算例,我们的方法误差上升了2 dB.

同样计算了一个半径为3λ的PEC半球,平面波垂直于半球平面入射.计算结果如图3和表2所示,与传统方法相比,MoM区域未知数个数几乎相同,耦合项的计算时间明显减少,εRMS上升了2.6 dB.

(a) 模型

(b) 双站RCS图3 半径为3λ的半球模型及其RCS仿真

未知数个数耦合项计算时间/sεRMS/dB近场Gordon近似混合法201805764.5167传统混合法2030017091.9029

3 结 论

本文提出了一种新的MoM-PO混合方法,用Gordon积分计算散射体亮区对暗区的作用,并加入近场近似处理.该方法避免了耦合项计算过程中积分方程的计算,因而可以在PO区域采用较大的面元进行剖分,有效地降低了耦合项的计算时间.从仿真结果来看,近场Gordon积分近似的MoM-PO混合方法能够准确地计算目标的散射,与传统的混合法相比,误差增加范围不超过3 dB.

[1] 潘小敏, 盛新庆. 电特大复杂目标电磁特性的高效精确并行计算[J].电波科学学报, 2008, 23(5): 888-893.

PAN X M, SHENG X Q. Efficient and accurate parallel computation of electromagnetic scattering by extremely large targets [J]. Chinese journal of radio science, 2008, 23(5): 888-893. (in Chinese)

[2] RAO S M, WILTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE transactions on antennas and propagation, 1982, 30(3): 409-412.

[3] 陈博韬, 雷振亚, 谢拥军,等. 基于改进物理光学法的电大目标双站RCS的预估[J]. 电波科学学报, 2010, 25(5): 960-965.

CHEN B T, LEI Z Y, XIE Y J, et al. Bistatic RCS Prediction with improved PO method for electrically large targets[J]. Chinese journal of radio science, 2010, 25(5): 960-965. (in Chinese)

[4] Medgyesi-Mitschang L, WANG D S. Hybrid solutions for scattering from perfectly conducting bodies of revolution[J]. IEEE transactions on antennas and propagation, 1983, 31(4): 570-583.

[5] JAKOBUS U, LANDSTORFER F M. Improved PO-MM hybrid formulation for scattering from three-dimensional perfectly conducting bodies of arbitrary shape[J]. IEEE transactions on antennas and propagation, 1995, 43(2): 162-169.

[6] JAKOBUS U, LANDSTORFER F M. Improvement of the PO-MoM hybrid method by accounting for effects of perfectly conducting wedges[J]. IEEE transactions on antennas and propagation, 1995, 43(10): 1123-1129.

[7] WEI X C, LI E P. Wide-band EMC analysis of on-platform antennas using impedance-matrix interpolation with the moment method-physical optics method[J]. IEEE transactions on electromagnetic compatibility, 2003, 45(3): 552-556.

[8] CHEN M, ZHANG Y, ZHAO X W, et al. Analysis of antenna around NURBS surface with hybrid MoM-PO technique[J]. IEEE transactions on antennas and propagation, 2007, 55(2): 407-413.

[9] 龚主前, 朱国强, 秦家银.MM-PO混合法中一致性劈面绕射电流研究[J].电波科学学报, 2008, 23(3): 576-579.

GONG Z Q, ZHU G Q, QIN J Y. Uniform expressions for the diffracted currents on the wedge surface for the MM-PO technique[J]. Chinese journal of radio science, 2008, 23(3): 576-579. (in Chinese)

[10]LIU Z L, WANG C F. Efficient iterative Meth-od of moments-physical optics hybrid technique for electrically large objects[J]. IEEE transactions on antennas and propagation, 2012, 60(7): 3520-3525.

[11]GORDON W B. Far field approximations to the kirchhoff-helmholtz representation of scattered fields[J]. IEEE transactions on antennas and propagation, 1975, 23(7): 590-592.

[12]LEGAULT S R. Refining Physical Optics for Near-field Computations[J]. Electronics Letters, 2004,40(1)：71-72.

[13]盛新庆. 计算电磁学要论[M]. 北京: 科学出版社, 2004,16-72.

孔蓓蓓 (1990-),女,甘肃人,北京理工大学博士研究生,研究方向为电磁场与微波技术.

盛新庆 (1968-),男,安徽人,北京理工大学教授,博士生导师,2001年度中国科学院“百人计划”入选者.2004年度教育部长江学者特聘教授.主要从事计算电磁学、目标电磁特性与探测技术、隐身目标分析与设计、天线分析与设计、电磁环境预测技术等方面的研究.

Efficient hybrid MoM-PO technique with near-field Gordon integral

KONG Beibei SHENG Xinqing

(CenterforElectromagneticSimulation,SchoolofInformationandElectronics,BeijingInstituteofTechnology,Beijing100081,China)

For the electromagnetic calculation of electrically large conducting object, a new hybrid method of moments-physical optics(MoM-PO) technique is presented to overcome the time-consuming in calculating the coupling term of PO region and MoM region with the increase of the target size by using the conventional hybrid MoM-PO method. The near-field scattering is calculated by Gordon integral to avoid the calculation of the integral equation of the coupling term of the conventional method and to increase the mesh size of PO region, which provides the possibility to reduce the computational time and computer memory. The results of numerical examples indicate the effectiveness of the new method. Compared with the traditional hybrid MoM-PO method, the computational time of the coupling term is reduced. Meanwhile, appropriate accuracy can be achieved.

MoM; PO; hybrid method; gordon integral

10.13443/j.cjors.2015110603

2015-11-06

国家自然科学基金(61371002)； 111引智计划(B14010)

O441.4

A

1008-9268(2016)04-0786-05

孔蓓蓓, 盛新庆. 利用近场Gordon积分近似的矩量法-物理光学混合方法[J]. 电波科学学报，2016,31(4):786-790.

KONG B B, SHENG X Q. Efficient hybrid MoM-PO technique with near-field Gordon integral[J]. Chinese journal of radio science，2016,31(4):786-790. (in Chinese). DOI: 10.13443/j.cjors.2015110603

联系人： 孔蓓蓓 E-mail: kongbeibei@bit.edu.cn