动平台下导航卫星多目标自跟踪方法研究

魏海涛，杨俊武，蔚保国，尹继凯

(1.卫星导航系统与装备技术国家重点实验室,河北 石家庄 050081；2.河北省卫星导航技术与装备工程技术研究中心，河北 石家庄 050081；3.西安卫星测控中心，陕西 西安 710043)



动平台下导航卫星多目标自跟踪方法研究

魏海涛1，2，杨俊武3，蔚保国1，2，尹继凯1，2

(1.卫星导航系统与装备技术国家重点实验室,河北 石家庄 050081；2.河北省卫星导航技术与装备工程技术研究中心，河北 石家庄 050081；3.西安卫星测控中心，陕西 西安 710043)

针对动平台下阵列天线对导航卫星自跟踪测角的问题，提出了一种采用导航信号解扩与阵列空间谱估计相结合的方法。通过信号解扩提高阵列接收的信噪比，通过MUSIC、ESPRIT和Mininorm等算法保证DOA估计的性能。仿真结果表明，3种算法的精度均能够达到0.1°，比较分析了不同算法的计算复杂度，提出了降低计算复杂度的方法。

卫星导航；阵列天线；空间谱；自跟踪

0 引言

在动平台下对卫星、航天器等目标的跟踪通常有2种方式：程序跟踪方式和自跟踪方式[1]，程序跟踪根据平台自身的姿态信息、运动参数和跟踪目标的运动参数等信息计算动平台跟踪天线指向的方位和俯仰参数；自跟踪方式通过对卫星、航天器等目标发射的信号进行处理，得到目标与动平台跟踪天线指向的方位和俯仰参数,从而产生高质量的波束[2]。通常，导航卫星的轨道参数可从导航电文中获得[3]，当动平台姿态、运动参数信息可准确获得时，动平台的卫星导航接收机可采用程序跟踪方式，产生精确的目标波束，实现高精度测量；当动平台姿态、运动参数信息无法准确获得时，需要对卫星目标进行测角和自跟踪，完成对导航卫星的跟踪和测量[4]。

当动平台卫星导航接收机采用阵列天线时，通常可采用最小均方算法[5]、递归最小二乘算法[6]等自适应抗干扰算法，自适应抗干扰算法主要针对干扰条件下的导航信号接收，以信干比为评估准则[7]，无法精确获得导航卫星的空间角度信息。本文采用阵列信号处理理论中的空间谱估计技术，通过解扩处理获得较高的信噪比，实现高精度的波达方向(Direction of Arrival)估计，在动平台下获得多颗导航卫星的空间角度信息[8]，能够对导航卫星进行精确波束形成[9]，从而实现动平台下导航卫星多目标的自跟踪。

1 数学模型

1.1 卫星导航信号模型

以GPS为例，假设在阵列天线的远场存在P个GPS卫星，所有到达阵列的波前均可以近似为平面波，信号满足窄带条件，即阵列天线接收到信号的幅度和相位于某个时刻在整个阵列孔径上的变化是可以忽略不计的，阵元间的波前传播可以近似为简单的相移。则第i颗GPS导航卫星的信号可以表示为：

xi(t)=bi(t)ci(t)ej(2πf0t)。

式中，bi(t)为导航电文数据符号；ci(t)为导航卫星对应的伪码序列；f0为信号的载波频率。

对于由M个接收天线组成的阵列，其k时刻的接收的卫星i的信号可以表示为：

xi(k)=a(θi)bi(k)ci(k)ejφi+ni(k)。

式中，a(θi) 和φi分别为卫星i的方向矢量和相位偏移；bi(k)为GPS电文数据符号(包括星历信息等)，ni(k)为独立同分布的加性高斯白噪声；ci为第i颗卫星的伪随机序列码，定义如下:

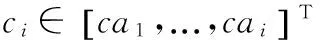
式中，cai是每颗卫星唯一对应的C/A码序列。

1.2 信号处理模型

对于GPS信号，C/A码长度为1 023的Gold码，伪码周期为1 ms，在一个GPS数据符号内重复20次，其扩频处理增益可以达到43 dB。

将期望卫星i的扩频码ci(t-τi)对阵列的接收信号向量x(t)进行滤波(解扩)，处理后信号的第n个比特为：

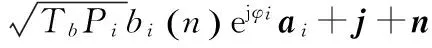
式中,θi、τi和Pi分别为第i颗卫星信号到达接收天线阵列的波达方向、时延和增益，那么，解扩信号yi的协方差矩阵为:

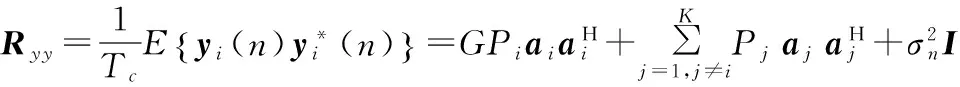
式中，G=Tb/Tc为扩频增益；Tb为比特间隔；Tc为码片间隔；Pj为不同扩频码间产生的干扰功率。

可见，解扩后使得信号功率变为原来的G倍，相对于干扰功率Pj(j≠i)有明显增加，则期望卫星i的等效方向向量ai是与解扩后信号协方差矩阵Ryy的最大特征值相对应的特征向量，从而解决了直接利用阵列接收信号向量协方差矩阵Rxx的特征值分解无法确定ai的问题。

2 多目标测角方法

2.1 解扩后MUSIC算法

多重信号分类法(MUSIC)于1968年首先由Schmidit首先提出[10]，是利用接收数据的协方差矩阵分离出信号子空间和噪声子空间，利用信号方向向量与噪声子空间的正交性来构成空间扫描谱，实现信号的DOA估计。

首先，对接收的GPS信号进行解扩处理，并计算信号的协方差矩阵：

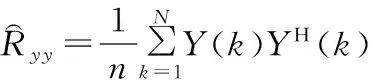
最后，计算P(θ)，并搜索谱峰，判定信号的DOA参数。

2.2 解扩后ESPRIT算法

旋转不变子空间算法(ESPRIT)由Roy R.和Kailath T.在1989年提出[11]，该算法充分利用相邻2个子阵之间存在的子阵间的旋转不变性。ESPRIT算法也是一种基于子空间的算法，具有闭式解，不需要谱峰搜索，运算量相对较小，但对阵列结构也有严格要求，即阵列要满足所谓的平移不变性。

对于2个几何结构完全相同且间距已知的子阵，接收数据分别为：

式中，φn(n=1,2,…,N)表示第n个信号在2个子阵上的相位差，Φ称为旋转因子：

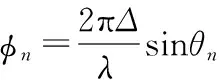
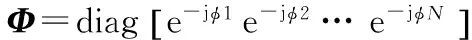
可见，只要得到Φ的值，即可以求出信号的DOA，将2个子阵数据合并得：

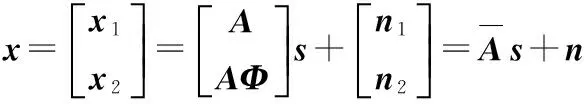
由上式可求得数据协方差矩阵R，特征分解后得到信号子空间US和噪声子空间UN，根据信号子空间性质可知，存在可逆矩阵T，使得

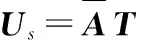
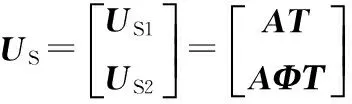
由上式可得，US1及US2满足关系：

US2=US1T-1ΦT=US1Ψ。

式中，Ψ=Τ-1ΦΤ，可以看出，Ψ和Φ为相似矩阵，对Ψ进行特征分解得到N个特征值，即可得到信号DOA。

2.3 解扩后Mininorm算法

由Kumaresan and Tufts提出的最小范数算法(Mininorm)[12]也是一类DOA估计方法，最小范数矢量是位于噪声子空间的向量，其中第一个元素为1，可以写为：

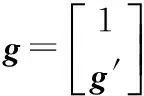
DOA估计其峰值:

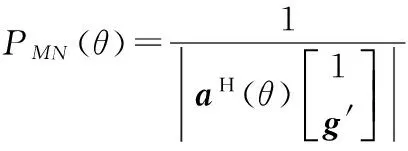
为了确定最小范数矢量g，Qs是信号子空间，其列构成信号子空间的基。Qs写作:

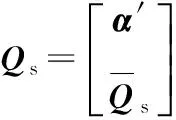
由于g位于噪声子空间,正交与Qs，α包含所有信号特征矢量的第一个元素,所以有

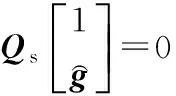
可得

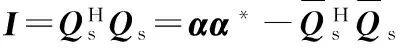
利用最小范数可获得:

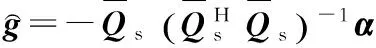
因此有

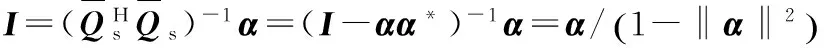
g可写为:

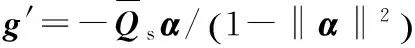
一旦g计算出来,即可获得信号的DOA估计。

3 多目标测角方法比较

3.1 测角性能分析

仿真条件：采用8阵元半波长等间距的均匀线阵，二维阵列与线阵原理相同，射频频率1.57 GHz，中频频率10 MHz，采样频率25 MHz，GPS单数据比特内20次C/A码重复周期，码速率为1.023 Mcps，4颗GPS卫星分别位于-40°、-28°、8°和46°(法线方向为0°)。在100次蒙特卡罗仿真结果如下：

不同信噪比条件下MUSIC算法、ESPRIT算法和Mininorm算法的性能如图1所示，从图1中可看出，测角性能与信噪比相关，在低SNR情况下，MUSIC算法和ESPRIT算法性能较好，Mininorm算法的测角性能较差。阵元数量与测角性能的关系如图2所示，从图2中可以看出，6阵元以上，MUSIC算法、Mininorm算法与ESPRIT方法的测角精度均可达到0.1°以内。

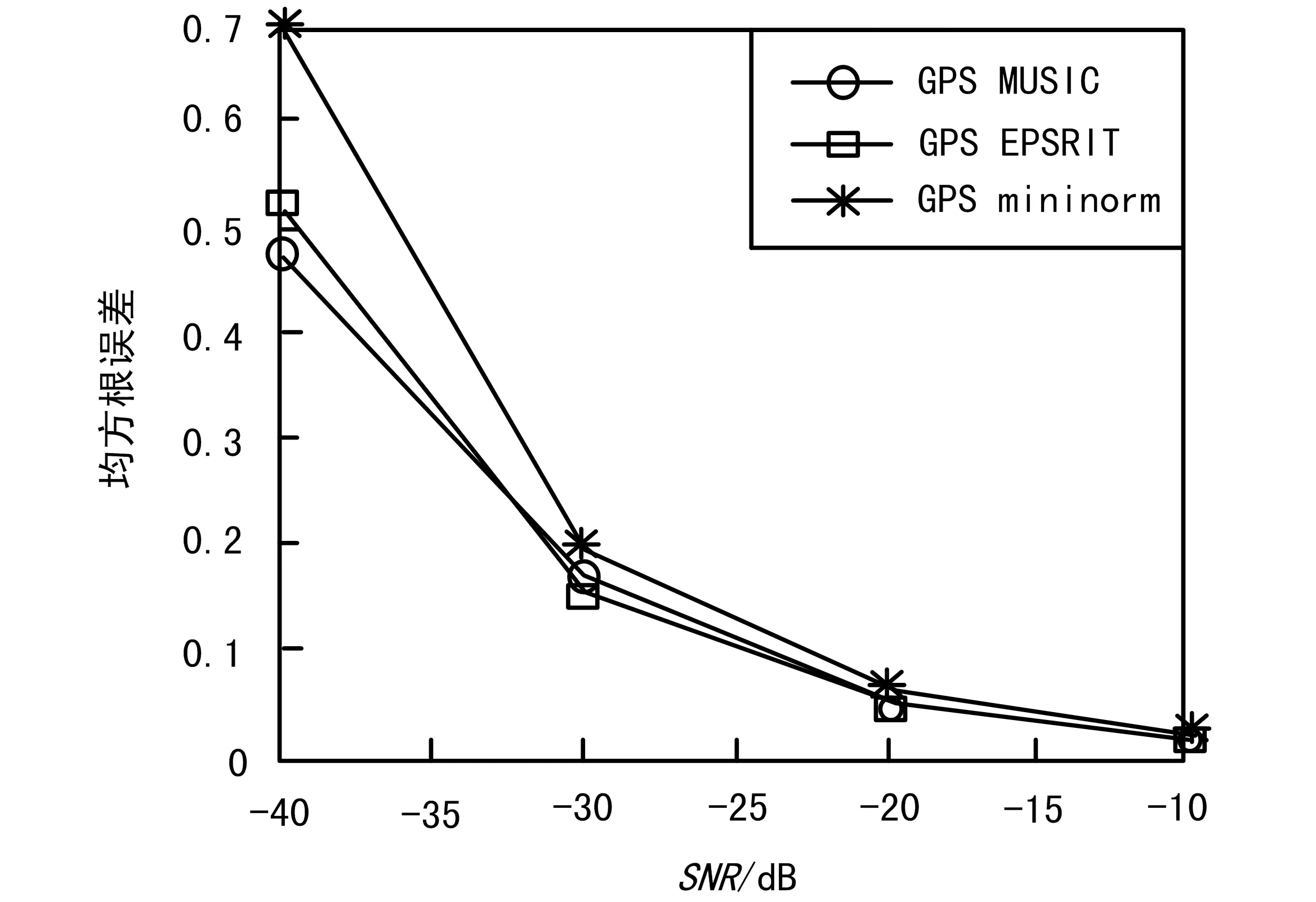
图1 不同信噪比测角性能比较

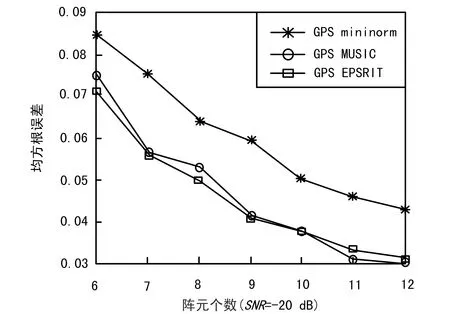
图2 不同阵元个数测角性能比较

3.2 计算复杂度分析

信源数为r,阵元数为M，快拍数为N，ESPRIT方法需要估计维数是M的协方差矩阵并对其做特征值分解，所要求的运算次数为O(M2N)+O(M2);MUSIC方法同样需要估计维数是M的协方差矩阵并对其作特征值分解，所要求的运算次数为O(M2N)+O(M3)。此外，一维搜索所需的计算量与搜索步长有关，其谱函数需计算L次。例如，空域搜索范围为(-60°～60°)时，搜索步长取0.1°，那么L=1 200次。单次谱函数计算量为O(MN)，则总的一维搜索的计算量为O(LMr)；Mininorm算法比MUSIC算法的复杂度稍高。通常，在工程应用中一般采用多级维纳滤波器(MSWF)的递推算法简化子空间分解，从而降低计算复杂度。

4 结束语

针对动平台下对导航卫星自跟踪测角的问题进行了研究，提出了采用基于阵列天线的信号解扩和空间谱估计算法进行DOA估计的方法，该方法避免了获取动平台的姿态信息，能够自主的获取导航卫星与GPS天线的相对位置信息，从而进一步开展波束形成操作，以提高系统的抗干扰、抗多径等。在实际工程应用中，阵列存在一定的幅相误差，其性能也会受到影响，因此，进一步研究阵列误差的自校准是后续的研究重点。

[1] 姚 勇.低轨卫星自跟踪技术分析[J].无线电工程,2011,41(10):17-20.

[2] 郑在齐.用于船上卫星定位稳定跟踪模型及其动态性能分析[J].现代防御技术,1993(5):15-38.

[3] HEGARTYC J,KAPLAN E D.GPS原理与应用[M].北京：电子工业出版社,2007：37-67.

[4] 李瑞榜.扩频信号跟踪测角技术研究[J].无线电工程，2004，34(1):31-49.

[5] 尚晓辉,宋晓辉,张 玉.阵列抗干扰射频接收机设计[J].无线电工程,2015,45(5):43-45.

[6] 唐 恬,姜 军,张 平.一种新的天线阵列盲自适应波束形成算法[J].无线电工程,2006,36(3):23-25.

[7] 陈 强.卫星导航接收机的抗干扰天线设计[J].无线电工程,2011,41(10):33-36.

[8] 李 淳.天基电子侦测中的阵列信号处理技术[J].无线电通信技术,2009,35(6):37-39.

[9] 尹继凯.二维阵列天线方向图综合算法研究[J].无线电通信技术,2002,28(5):21-23.

[10] SCHMIDT R O.Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Trans.Antennas Propagate,1986(34):276-280.

[11] ROY R，PAULRAJ A，KAILATH T.ESPRIT-a Subspace Rotation Approach to Estimation of Parameters of Cissoids in Noise[J].IEEE ASSP，1989，34(5):1 340-1 342.

[12] KUMARESAN R,TUFTS D W.Estimating the Angles of Arrival of Multiple Plane Waves[J].IEEE Trans,1983,19(1):134-139.

魏海涛 男，(1979—)，高级工程师。主要研究方向：卫星导航、阵列天线。

蔚保国 男，(1966—)，研究员。主要研究方向：卫星导航、阵列天线、信号处理。

Auto-tracking Method for Navigation Satellites on Moving Station

WEI Hai-tao1，2,YANG Jun-wu3,YU Bao-guo1，2,YIN Ji-kai1，2

(1.StateKeyLaboratoryofSatelliteNavigationSystemandEquipmentTechnology,ShijiazhuangHebei050081,China; 2.HebeiSatelliteNavigationTechnologyandEquipmentEngineeringTechnologyResearchCentre,ShijiazhuangHebei050081,China; 3.Xi’anSatelliteControlCenter,Xi’anShaanxi710043,China)

In view of the problem of auto-tracking of navigation satellites using an array antenna on moving station,a method based on signal de-spreading and array spatial spectrum estimation is proposed,which can improve the signal noise ratio and the precision of direction of arrival using algorithms of MUSIC,ESPRIT and Mininorm.The performance of the algorithms is simulated,and the precision can reach 0.1°.The computational complexity of different algorithms is analyzed,and the method for reducing computational complexity is presented.

satellite navigation;array antenna;spatial spectrum;auto-tracking

10.3969/j.issn.1003-3106.2016.12.10

魏海涛，杨俊武，蔚保国，等.动平台下导航卫星多目标自跟踪方法研究[J].无线电工程,2016,46(12):39-42.

2016-09-07

河北省“三三三人才”培养基金资助项目(A201400116)。

TN911

A

1003-3106(2016)12-0039-04