主瓣干扰下单脉冲测角技术研究
2016-12-14张同会秦轶炜
张同会,秦轶炜
(上海航天电子技术研究所,上海 201109)
主瓣干扰下单脉冲测角技术研究
张同会,秦轶炜
(上海航天电子技术研究所,上海 201109)
针对二维数字阵列雷达在主瓣干扰下的测角问题,给出了四通道单脉冲测角方法。相对传统数字阵列雷达的三通道测角方法,增加一个双差通道,应用主瓣干扰对消技术,在方位和俯仰方向上分别形成和差波束,然后利用单脉冲技术测角。形成的和差波束在干扰方向形成零陷,同时保持原来的单脉冲比。仿真结果显示,该技术可以在抑制主瓣干扰的同时保持较高的测角精度,且测角精度与信噪比、目标和干扰方向有关。
数字阵列雷达;双差通道;主瓣对消;单脉冲;测角精度
0 引言
现代电子战技术和装备的发展方向是宽频带、大功率、高精度,同时自适应管理水平、一体化程度不断提高,协同作战能力不断增强[1]。事实上,电磁干扰对雷达的软杀伤威胁已经改变了传统的雷达设计观念,雷达在复杂电磁干扰环境下的生存能力已经成为决定战争双方胜负的关键因素[2]。
根据干扰从雷达天线进入的方向可以分为主瓣干扰和副瓣干扰。对于抑制副瓣干扰,传统的低副瓣天线技术[3]、旁瓣相消[4]、旁瓣匿影[5]以及近年来提出的自适应波束形成技术(ADBF)[6]都有很好的应用效果,在抑制干扰的同时可以进行目标检测和角度估计。对于主瓣干扰,ADBF虽然可以抑制干扰,但会使波束主瓣严重变形,无法对目标进行测角[6]。
基于阻塞矩阵的方法[6]和盲源分离的方法[7]可以有效抑制主瓣干扰,但是这2种算法中均涉及大量矩阵运算和矩阵分解操作,不利于硬件实时处理。文献[8]介绍了一种四通道雷达抗干扰方法,但要求主瓣必须对准干扰源。文献[9-10]分别介绍了阵元级和子阵级下应用四通道主瓣对消的单脉冲测角方法,对主瓣内的干扰均可以抑制,且运算简单,但均未对测角精度进行讨论。本文介绍了应用主瓣对消的单脉冲测角技术,并通过仿真分析了影响其测角精度的因素。
1 二维数字阵列雷达信号模型
天线阵面示意图如图1所示,设平面阵列放置于xoy平面,由M×N个天线单元组成组成,M为行数,N为列数,在x和y方向的阵元间距均为d,θ和φ分别表示俯仰角和方位角。
假设以(0,0)处的阵元为参考阵元,则阵面的第m行、第n列阵元与(0,0)阵元之间的空间相位差为:
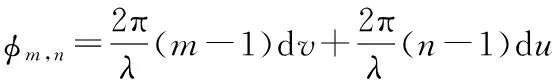
(1)
式中,u=cosθsinφ;v=sin(θ)。由此得阵列的二维导向矢量为:
a(u,v)=[1,…,exp(jφm,n),…,exp(jφM,N)]T。
(2)
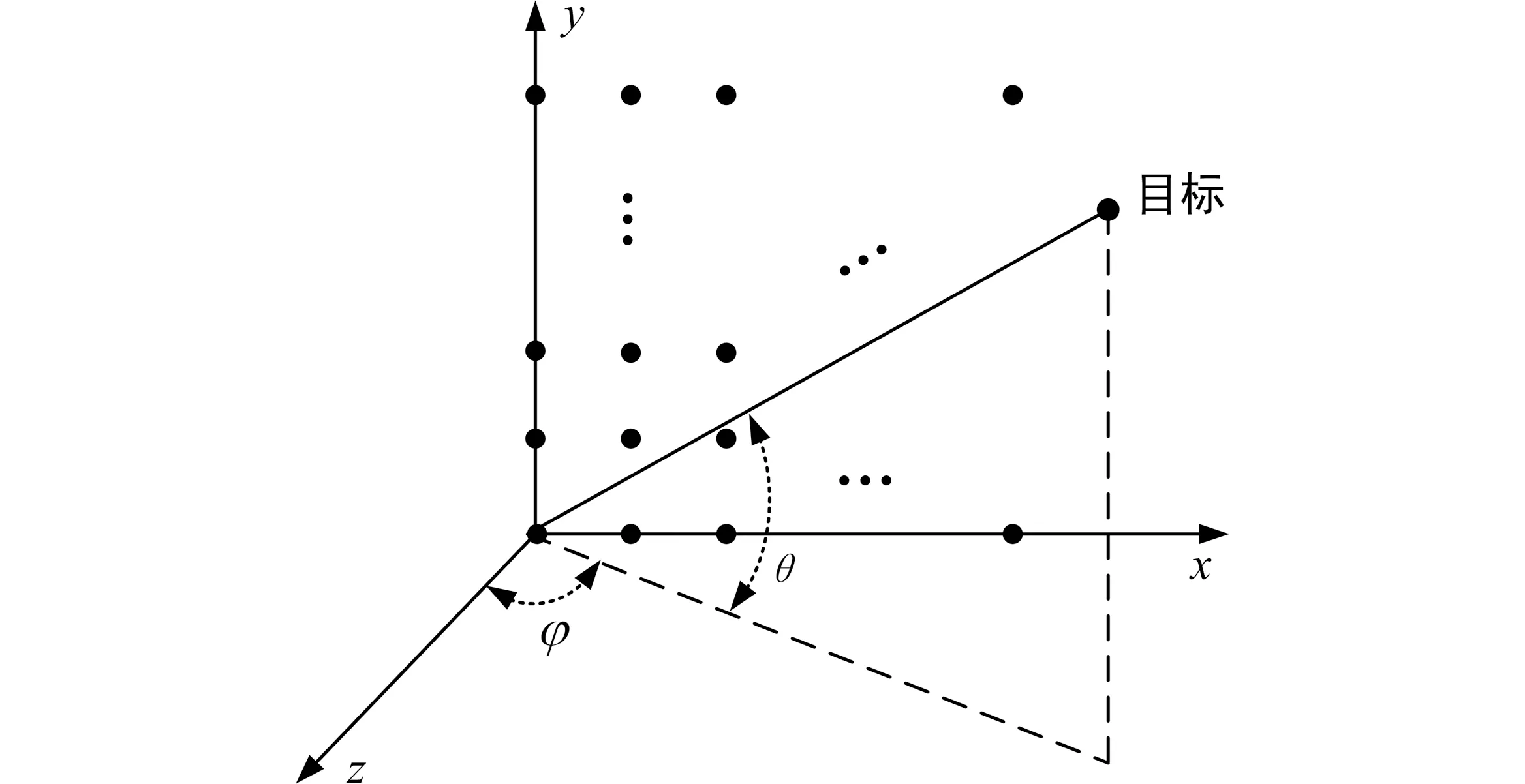
图1 天线阵面示意
假设空间存在互K个相统计独立的远场窄带源sk(t),其中k=1,…,K。其导向矢量分别为ak,并存在与信号不相关的M×N个加性高斯白噪声,用N(t)表示,则阵列在t时刻接收的信号矩阵为:
X(t)=As(t)+N(t)。
(3)
式中,
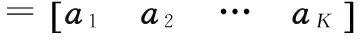
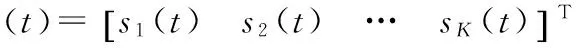
假设权值矢量w=[1,…,wm,n,…,wM,N]T,其中wm,n表示对阵面的第m行、第n列阵元加权,通过对X(t)加权,可以得到输出:
y(t)=wHX(t)。
(4)
2 基于窗函数的单脉冲测角系统
单脉冲测角需要同时形成和差波束,通过使阵列左右两边单元的相位同相相加得到和波束,反向相加得到差波束。二维数字阵列雷达为了测目标俯仰角和方位角需要3个通道:和通道、方位差通道和俯仰差通道,通道加权示意图如图2所示。
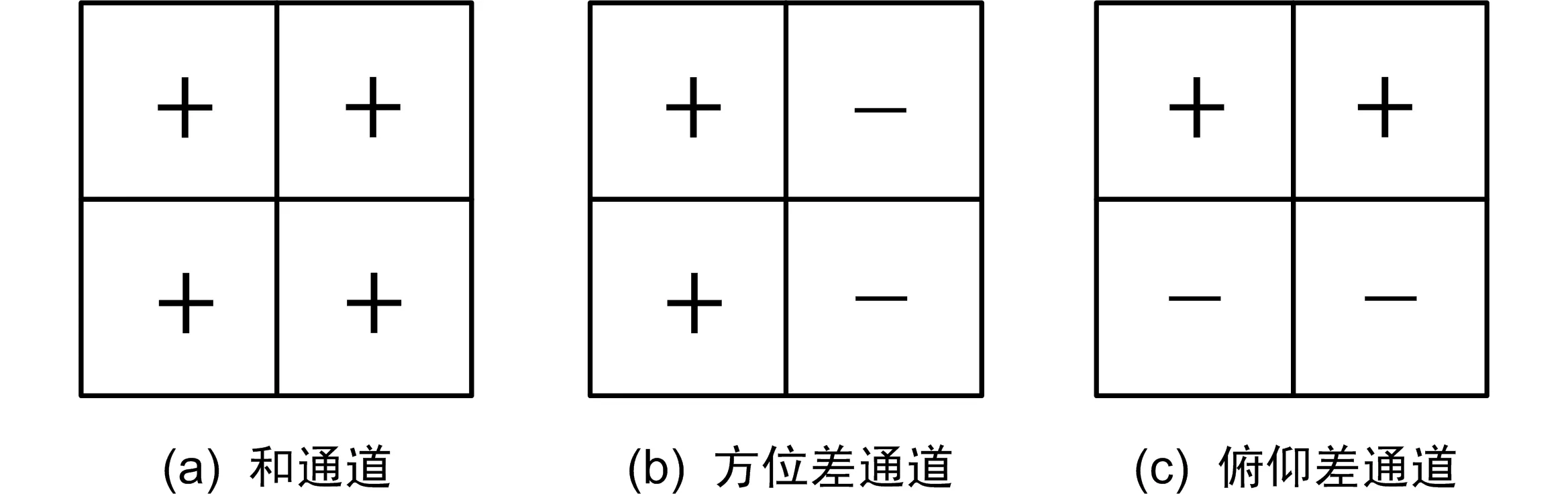
图2 通道加权示意
yΣ(t)=wHΣX(t),
(5)
yΔa(t)=wHΔaX(t),
(6)
yΔe(t)=wHΔeX(t)。
(7)
式中,[·]H表示共轭转置。然后提取归一化角误差信号[11]:
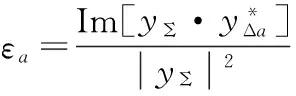
(8)
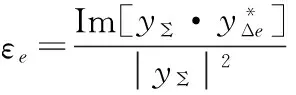
(9)
在波束指向两侧较小的角度范围内,可以通过角误差信号估计目标的角度为:
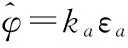
(10)
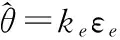
(11)
式中,ka和ke为比例系数。
3 主瓣对消原理
主瓣对消(MLC)是通过一套加权值消除一个方向上的主瓣干扰。权值的选取以最小功率输出为准则。
由于和通道与方位(俯仰)差通道对消干扰后只形成一个通道数据,因此无法利用单脉冲方法测量目标方位(俯仰)角。为了继续保持单脉冲测角性能,增加一个双差通道,其阵元的加权如图3所示,权值矢量为wΔΔ。
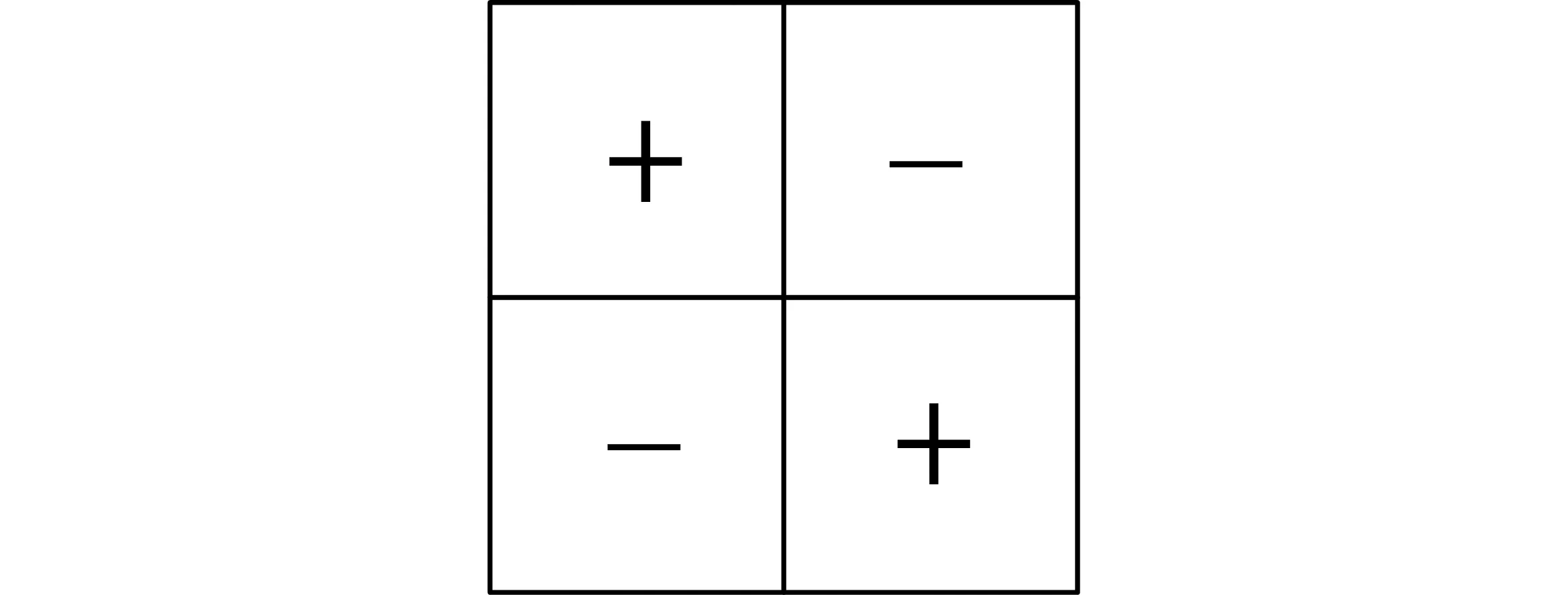
图3 双差通道加权示意
其通道输出为:
yΔΔ(t)=wHΔΔX(t)。
(12)
以对消主瓣的方位干扰,形成一个俯仰和通道和新的俯仰差通道为例。
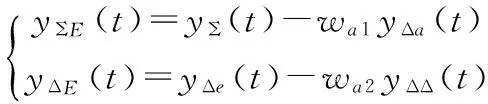
(13)
以yΣE(t)对消后输出功率最小分析最优权值的选取:
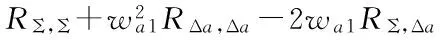
(14)
为了对消主瓣的俯仰干扰,形成一个方位和通道和新的方位差通道。
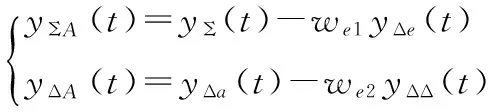
(15)
4 主瓣对消下的测角性能分析
对于平面阵方向图,合成阵列方向图等于合成行方向图与合成列方向图的乘积,即
f(u,v)=fa(u)fe(v)。
(16)
于是和通道、方位差通道、俯仰差通道和双差通道的阵列方向图为:
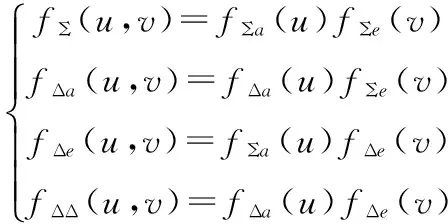
(17)
消除主瓣方位干扰后,得到的俯仰和、差方向图为:
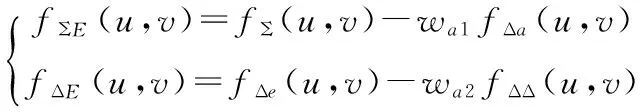
(18)
在强干扰环境下,干扰功率远大于目标回波和噪声的功率,因此,
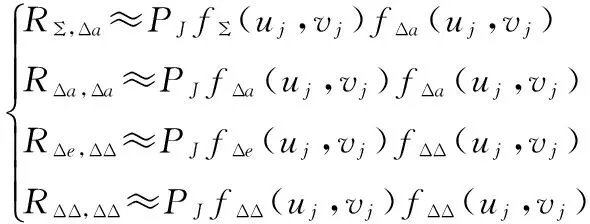
(19)
于是通道加权值可以表示为:
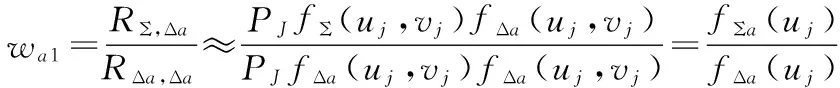
(20)
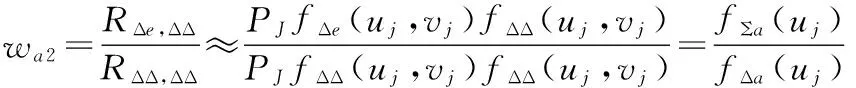
(21)
由此可见,wa1和wa2近似相等,实际采样计算时取
wa=(wa1+wa2)/2。
(22)
则对消干扰后的俯仰和、差方向图为:
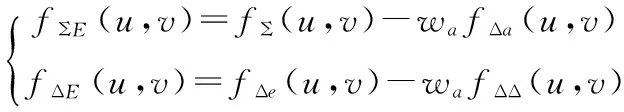
(23)
由式(17)和式(21)可得俯仰方向单脉冲比为:
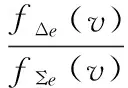
(24)
由式(24)可以看出,通过加权消除主瓣干扰后俯仰方向上仍然保持着原来的单脉冲比。在俯仰方向上消除主瓣干扰,方位方向单脉冲比有相同的结论。
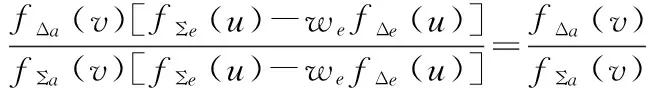
由以上分析可知,在主瓣干扰条件下,通过四通道主瓣对消技术可以在抑制干扰的同时继续保持单脉冲测角的性能。
5 仿真结果及分析
假设二维平面阵的大小为40×52,放置在xoy平面上,在沿y方向有40行,沿x方向有52列。目标所在方向为(φD,θD)=(0.1°,0.2°),干扰所在方向为(φJ,θJ)=(-0.5°,-0.5°),信号形式采用线性调频信号,带宽4 MHz,脉冲宽度30 μs,信噪比SNR=0 dB,干扰为高斯噪声,干噪比JNR=50 dB。
对消后波束方向如图4所示。
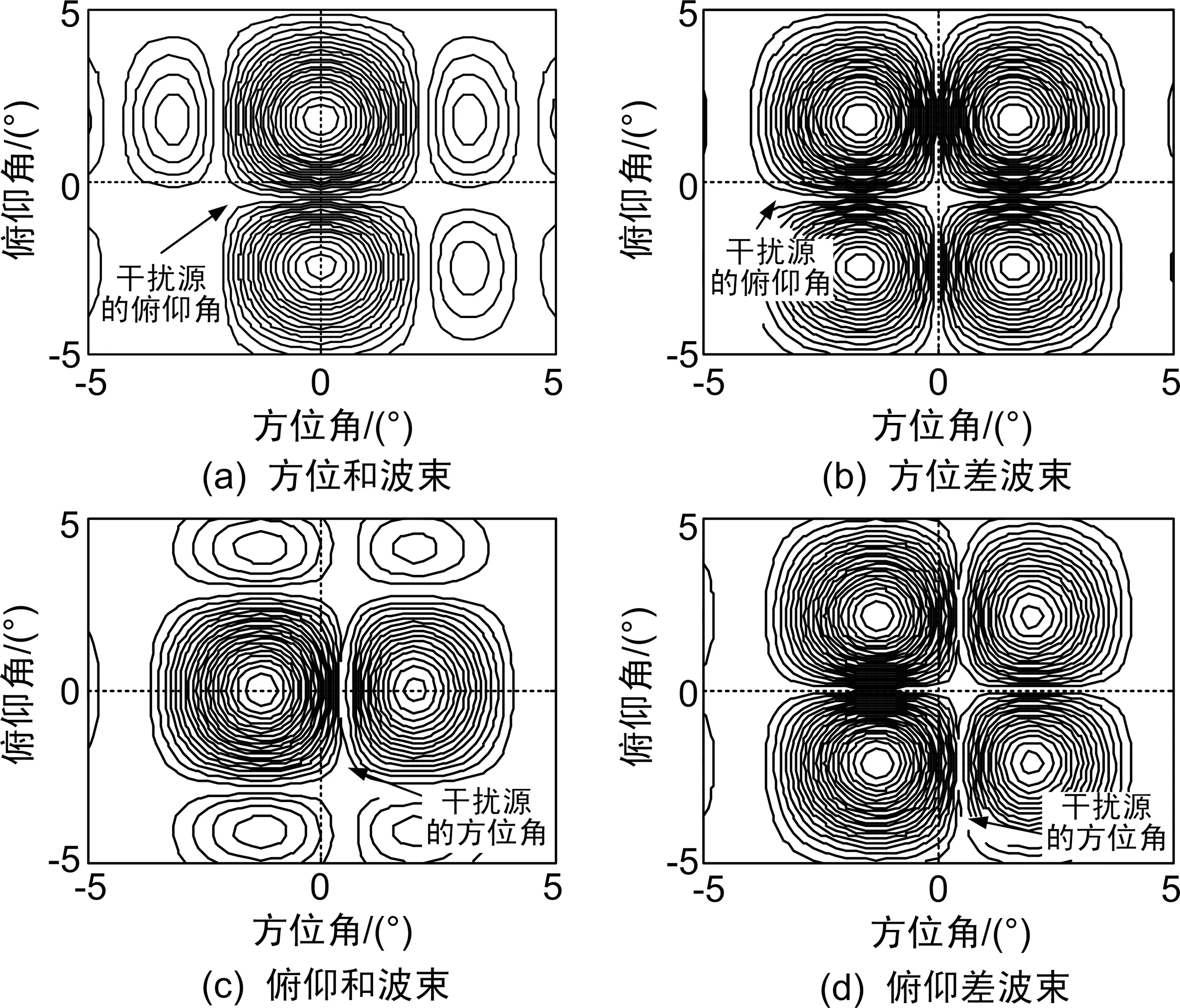
图4 对消后波束方向图
从图4可以看出,在主瓣对消俯仰干扰后,方位和波束、方位差波束在干扰所在的俯仰方向上形成了零陷;主瓣对消方位干扰后,俯仰和波束、俯仰差波束在干扰所在的方位方向上形成了零陷。
主瓣对消前后单脉冲比曲线图如图5所示。
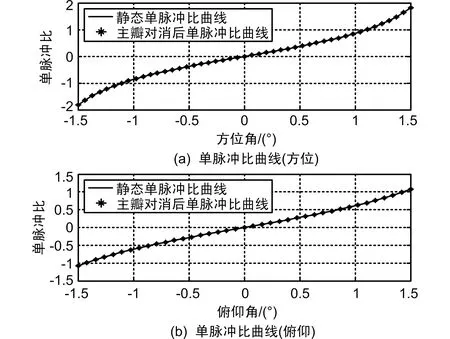
图5 主瓣对消前后单脉冲比曲线
从图5中可以看出,主瓣对消后俯仰方向和方位方向的单脉冲比曲线均与静态单脉冲比曲线一致。因此,采用主瓣对消技术,在对消干扰的同时仍然可以保持单脉冲测角技术的精度。
主瓣对消前后的脉压结果如图6和图7所示。
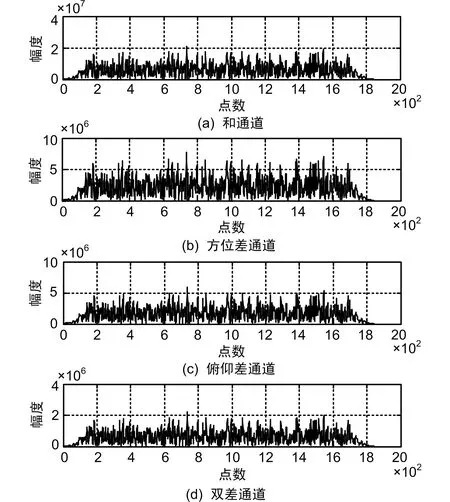
图6 主瓣干扰对消前脉压结果
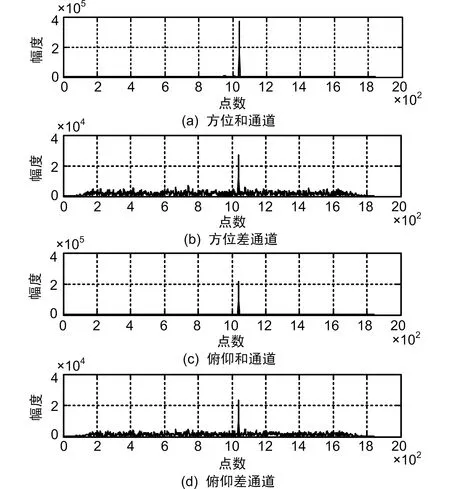
图7 主瓣干扰对消后脉压结果
在主瓣对消前信号完全淹没在干扰里,无法对目标进行检测和角度测量,主瓣对消后各个通道中的目标信号明显凸显出来。为了分析不同信噪比下的主瓣干扰对消下的测角精度,在不同信噪比下分别进行200次Monte Carlo实验做统计分析。
不同信噪比下的测角误差曲线图如图8所示。从图8中可以看出,应用主瓣干扰对消技术,在能满足一定的信噪比时,测角精度随信噪比的增加而提高,这和无干扰条件下的单脉冲测角精度结论一致[12-13]。
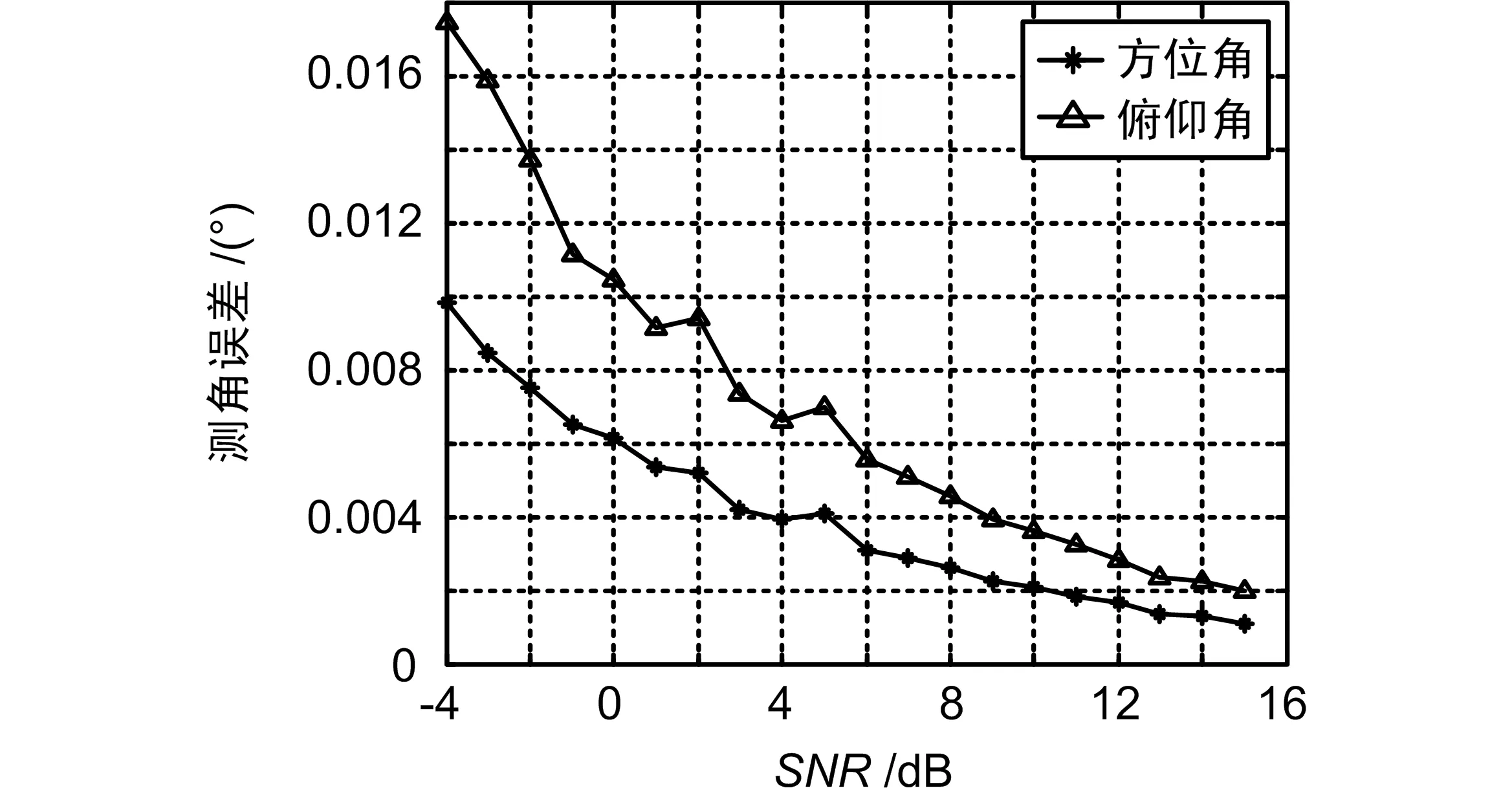
图8 不同信噪比下的测角误差
当目标在主瓣轴向方向时,主瓣干扰所在方向对测角精度的影响如图9所示。从图9中可以看出,干扰方向与目标方向相差越大,测角精度越高。这是因为当干扰方向与目标方向接近时,干扰零陷使阵列天线在目标方向的增益降低,接收信噪比下降导致的。
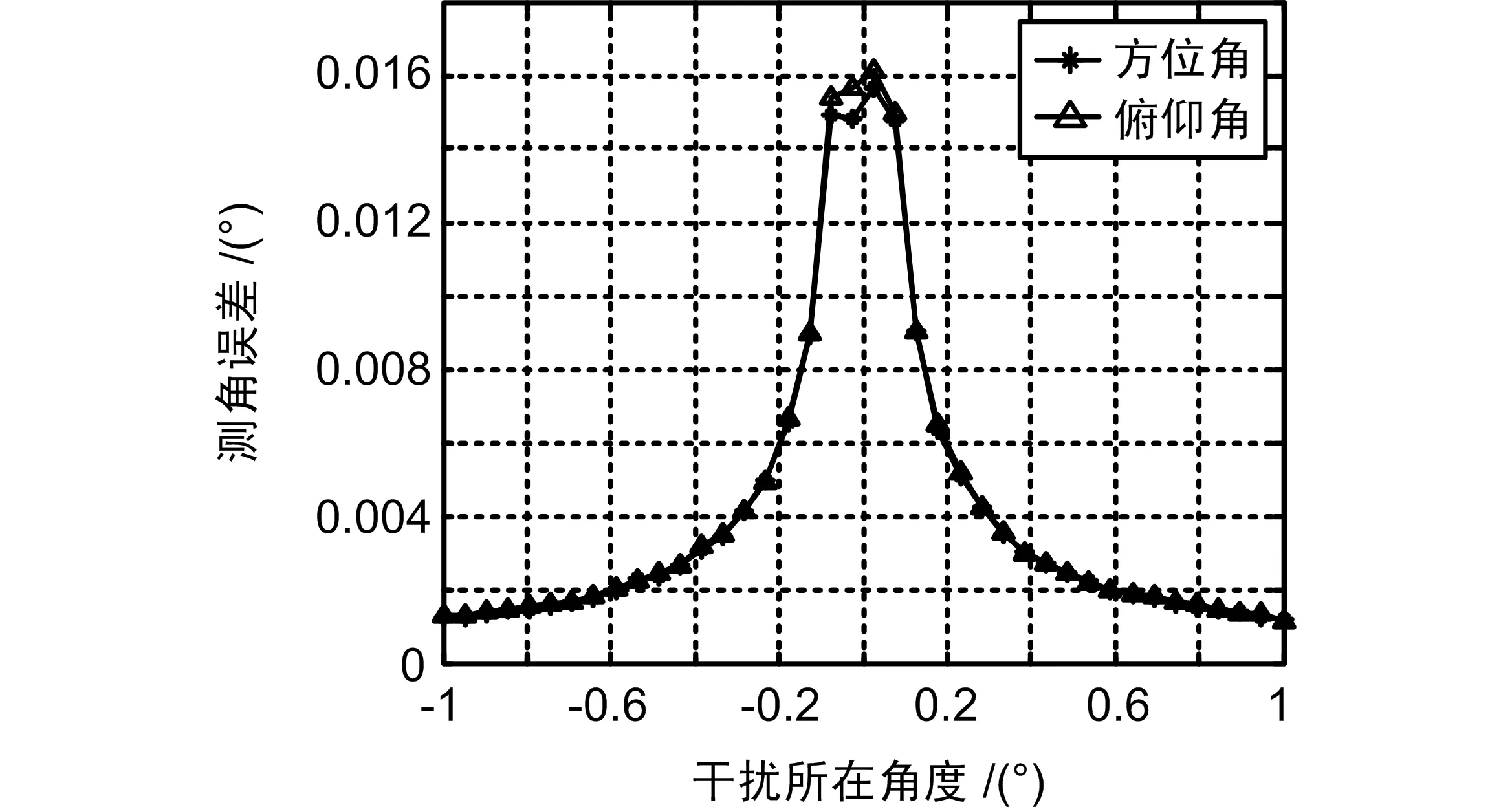
图9 干扰所在方向对测角精度的影响
6 结束语
本文介绍了一种针对二维数字阵列雷达在抑制主瓣干扰的同时保持单脉冲测角性能的方法,并分析了信噪比和干扰方向对测角精度的影响。仿真结果显示,在存在主瓣干扰的条件下,主瓣对消技术可以有效抑制干扰,且信噪比越大,干扰与目标方向差别越大,测角精度越高。本文对主瓣干扰条件下二维数字阵列雷达单脉冲测角系统设计具有借鉴作用。
[1] 王晓铭,王 玫.防空导弹武器抗干扰试验技术[J].上海航天,2013,2(30):34-38.
[2] 朱华邦,杜 鹃.雷达抗干扰技术的新特点及发展方向[J].飞航导弹,2004(5):52-54.
[3] 刘双青,蔡新举,占 超.雷达抗干扰技术现状及发展趋势[J].舰船电子工程,2013,8(230):7-14.
[4] 胡可欣,胡爱明.自适应旁瓣对消在雷达中的应用[J].火控雷达技术,2006,6(35):42-45.
[5] 胡可欣,胡爱明.旁瓣消隐技术在雷达中的应用[D].成都:电子技术学术,2006:315-317.
[6] 苏保伟,王永良,李荣峰,等.阻塞矩阵方法对消主瓣干扰[J].系统工程与电子技术,2005,11(27):1 830-1 832.
[7] 王建明,伍光新,周伟光.盲源分离在雷达抗主瓣干扰中的应用研究[J].现代雷达,2010,10(32):46-49.
[8] 徐安祺,赵婵娟,何 劲.四通道单脉冲测角抗主瓣干扰技术研究[J].无线电工程,2016,46(2):41-43.
[9] YU K B,MURROW D J.Adaptive Digital Beamforming for Preserving Monopulse Target Angle Estimation Accuracy in Jamming[C]∥Sensor Array and Multichannel Signal Processing Workshop.Proceedings of the 2000 IEEE.IEEE,2000:454-458.
[10] 胡 航,张 皓.子阵级自适应单脉冲的四通道主瓣干扰抑制[J].电波科学学报,2009,24(5),820-825.
[11] 陈伯孝.现代雷达系统分析与设计[M].西安:西安电子科技大学出版社,2012.
[12] SHARENSON S.Angle Estimation Accuracy with A Monopulse Radar in The Search Mode[J].Aerospace and Navigational Electronics,1962 (3):175-179.
[13] 方棉佳,吕 涛.单脉冲和差波束测角的精度研究[J].雷达科学与技术,2013,12(6):645-649.
张同会 男,(1992—),硕士研究生。主要研究方向:信号与信息处理。
秦轶炜 男,(1982—),高级工程师。主要研究方向:信号与信息处理。
A Method of Angle Estimation with Monopulse under Mainlobe Jamming
ZHANG Tong-hui,QIN Yi-wei
(ShanghaiAerospaceElectronicTechnologyInstitute,Shanghai201109,China)
This paper is concerned with angle estimation under mainlobe jamming using monopulse method for two-dimension digital array radar.Sum beam and difference beam are formed for azimuth and elevation respectively,using Mainlobe Cancellation (MLC) technique by adding a double-difference channel.The mainlobe jamming is suppressed by nulling the sum and difference beam while preserving the monopulse ratio.The simulation results show that it has a high accuracy of angle estimation under mainlobe jamming.What’s more,the accuracy is related to the SNR and the directions of the target and the jamming.
digital array radar;double-difference channel;MLC;monopulse;accuracy of angle estimation
10.3969/j.issn.1003-3106.2016.12.07
张同会,秦轶炜.主瓣干扰下单脉冲测角技术研究[J].无线电工程,2016,46(12):26-30.
2016-08-29
国家国际科技合作专项基金资助项目(2012DFB10200)。
TN973.3
A
1003-3106(2016)12-0026-05
