上邻及弱上邻

王娣，卢 涛

（淮北师范大学数学科学学院，安徽 淮北 235000）

上邻及弱上邻

王娣，卢 涛

（淮北师范大学数学科学学院，安徽 淮北 235000）

首先给出了弱完全交既约元、余dcpo及way-up的概念；然后结合way-up关系和新的辅助关系定义了弱上邻的概念；最后,借助弱完全交既约元讨论了上邻及弱上邻在交半格、完备格及余dcpo不同背景下的性质.

way-up；弱完全交既约元；余dcpo；弱上邻；插入关系

既约元是格论中的一种特殊元素，具有一些很好的性质，在格论中占有重要的地位.Crawley等首先提出了完备格中完全并既约元的概念[1].文献[2]定义了一种新的并既约元：连续并既约元，并讨论了它的一些基本性质.文献[3]在完全并既约元和连续并既约元的基础上引入了弱完全并既约元的概念，讨论了各种既约元、素元和紧元的关系.文献[4]详细地给出了way-below、辅助关系的概念及其相关性质，其中包括way-below的插入性质.文献[5]和文献[2]引入了新的辅助关系:上邻和下邻.文献[6]提出了弱下邻的概念.受以上文献启发，本研究对偶地给出了弱完全交既约元、余dcpo及way-up的概念，并结合way-up关系和新的辅助关系定义了弱上邻的概念，然后借助弱完全交既约元讨论了上邻及弱上邻在交半格、完备格及余dcpo不同背景下的性质.

1 预备知识

定义1[5]设P为偏序集，对任意a、b∈P，如果a＜b，且对任意x∈P，a＜x＜b不成立，则称b是a的上邻，记作b≻a.

定义2[7]设L为交半格，对任意x、y、z∈L，如果z=x∧y蕴含x=z或y=z，则称z为L的交既约元.记M（L）={z∈L|z为交既约元}.

定义3[4]设L为完备格，a∈L，如果对于任意S⊆L，由a=∧S可推出a∈S，则称a为L的完全交既约元.记Q（L）={a∈L|a为完全交既约元}.

定义4[7]设L是偏序集，对于a∈L与S⊆L，规定

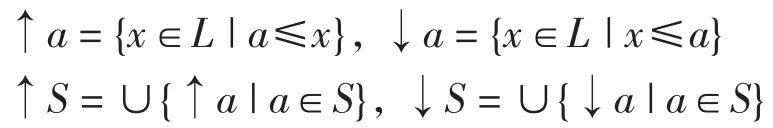
当S=↑S时，称S为上集；当S=↓S时，称S为下集.

定义5[7]设L为偏序集，F是L的非空子集，若F是余定向的上集，则称F为偏序集L的滤子.偏序集L的全体滤子组成的集合记作Fil（L）.

定义6 设L为余定向完备偏序集（以下简记为余dcpo)，a∈L，如果对于任意F∈Fil（L），由a=∧F可推出a∈F，则称a为L的弱完全交既约元.记RQ（L）= {a∈L|a为弱完全交既约元}.

由定义4可知1∉RQ（L），且在完备格中，完全

交既约元是弱完全交既约元.

定义7 设L为偏序集，x、y∈L，对任意余定向集M⊆L，当∧M存在，且y≥∧M时，存在m∈M，使得x≥m，则称x way-up于y，记作x≫y.当x≫x时，称x是L的余紧元.记K（L）={x∈L|x≫x}为L的所有余紧元.

注1 在偏序集L中，x≫y一定有x≥y，反之不然，见图1.

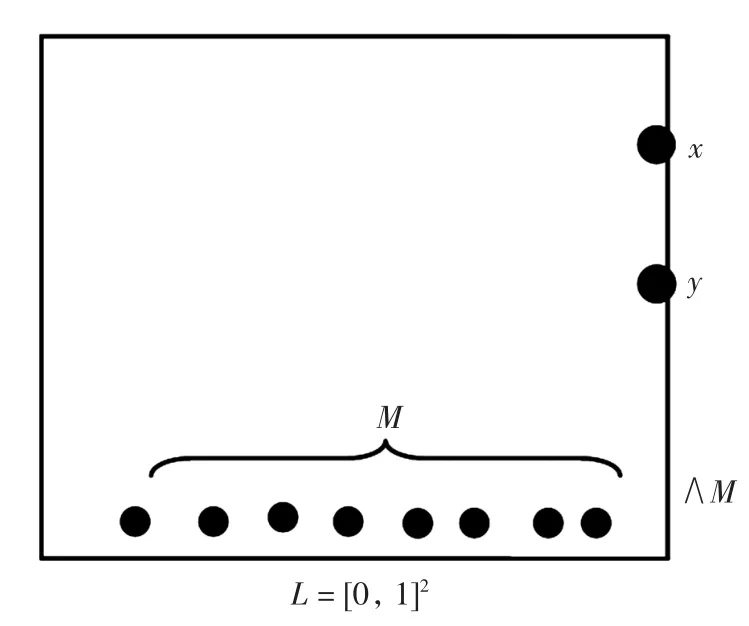
图1 x≥y，而x≫y不成立Fig.1 x≥y but not x≫y

引理1 设L是偏序集，对任意x、y、z、w∈L，“≻”为L上的辅助关系，则下列结论成立

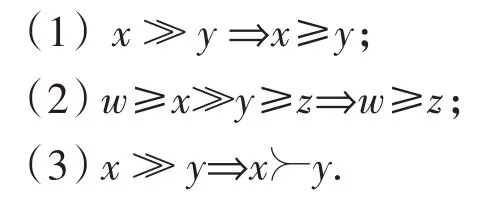
证明 （1）由于x≫y，任取余定向集M⊆L，如果∧M存在，且y≥∧M，存在m∈M，使得x≥m，故可取y=m，则有x≥y.

（2）由于x≫y，任取余定向集M⊆L，当∧M存在，且y≥∧M时，存在m∈M，使得x≥m，又w≥x≫y≥z，从而w≥x≥m，且由（1）可知w≥x≥y≥z，故可取y=m，当z≥∧M时，存在m∈M，使得w≥m，从而w≫z，再由（1）可得w≥z.

（3）假设命题不成立，则存在a∈L，使得x>a>y成立.又由（1）知x≥y，从而与x>a>y矛盾，故假设不成立，命题得证.

引理2 设L是交半格，对任意x、y、z∈L，若x∧y≫z，则x≫z且y≫z，从而有：若x∧y≻z，则x≻z且y≻z.

证明 假设当x∧y≻z时，x≻z或y≻z不成立，则由定义，存在a∈L，使得x>a>z或y>a>z.不妨设x>a>z成立，则x∧y≥a∧y≥z，这与x∧y≻z矛盾，从而假设不成立，命题得证.

2 主要结果

定义8 设L为偏序集，a、b∈L，≻为L上的辅助关系，若a≻b，且对任意x∈L，a≻x≻b不成立，则称a为b的弱上邻，记作a′≻b.

注2′≻实际上是不满足插入性质的辅助关系的特殊情况，规定a′≻b时，有a≥b.

定理1 设L是交半格，对任意x、y、z∈L，若x′≻z，y′≻z，则x∧y′≻z.

证明 假设x∧y不是z的弱上邻，则存在a∈L，使得x∧y≻a≻z成立.于是x≻a≻z，y≻a≻z，这与x′≻z，y′≻z矛盾，从而x∧y′≻z.

定义9 设L为完备格，对任意x∈L，若x′≻x，则称x为′≻-余紧元.记K′（L）为L的全体′≻-余紧元组成的集合，即K′（L）={x∈L|x′≻x}.

定理2 设L为格，对任意x、y∈L，若存在a∈L，使得x≻a，y≻a，则x‖y（x与y不可比较）.

证明 若x≻a，y≻a，则对任意x，有y>x>a不成立，对任意y，有x>y>a不成立，从而x‖y.

定理3 设L为交半格，对于x、y∈L，x≠y，x、y至少有一个是余紧元，若存在a∈L，使得x≻a，y≻a，则x‖y.

证明 由条件，不妨设y∈K′（L）.

（1）若x>y，则x>y≫y≥y≻a，进而有x≫y≻a，即x≻y≻a，矛盾.

（2）若y>x，则y>y≫y≥x≻a，从而有y≫x≻a，即y≻x≻a，矛盾.

综上可得x‖y.

定理4 设为L格，a∈M（L），则a至多有一个上邻.

证明 设a∈M（L），若a有2个上邻x、y，且x≠y，则由定理2得x∧y=a，而x>a，y>a，这与a∈M（L）矛盾.所以a至多有一个上邻.

定理5 设L为余dcpo，a∈M（L），则a至多有一个弱上邻.

证明 设x′≻a，y′≻a，则x≻a，y≻a且x∧y= a.因为a∈M（L），故有x=a或y=a.不妨设x=a，则y′≻x′≻a，于是y≻x≻a.由弱上邻的定义，有y≻x≻a，与x′≻a，y′≻a，矛盾，从而a至多有一个弱上邻.

定理6 设L为余dcpo，对任意a∈L，若a∈RQ（L），则a至少有一个弱上邻.

证明 设a∈RQ（L），则a≠0，且B={b∈L| b≻a}-{a}≠.因为L为余dcpo，则B也为余dcpo，进而∧B存在，∧B≥a.

（1）若∧B=a，对任意x∈B，及a∈RQ（L），则B不是余定向集，于是对任意b∈B，存在x、y∈B，使得x与b无关，且b≻a，y与b无关，且b≻a，则x、y中至少有一个是B中的极小元，即x、y中至少有一个是a的弱上邻.

（2）若∧B>a，不妨设∧B=b>a，设x∈L，使得b≻x≻a，则x∈B，从而x≥∧B=b，与x>b矛盾.故b是a的弱上邻.

综上，a至少有一个弱上邻.

推论 设L为余dcpo，若a∈RQ（L），则a有唯一弱上邻.

证明 先证存在性.由定理6知，对任意a∈L，若a∈RQ（L），则a至少有一个弱上邻.

再证唯一性.因为a∈RQ（L），从而a∈M（L），由定理5知此时a至多有一个弱上邻.故由存在性知a有且仅有一个弱上邻.

定理7 设L是完备链，则对任意a∈L，a没有弱上邻.

证明 设x∈L且x′≻a，则x≥a.由于L是完备链，故x≫a，于是存在y∈L，使得x≻y≻a，矛盾.从而命题成立.

3 结语

本研究在引入了弱上邻概念的基础上，探讨了弱上邻在交半格、完备格及余dcpo不同背景下的性质，并研究了上邻与弱上邻之间的本质特征.但关于上邻与弱上邻之间的联系及它们之间的等价刻画还未做深入研究，这将是今后该方面研究的一个方向.

[1]CRAWLEY P，DILWORTH R P.Algebraic Theory of Lattic[M].Englewood：Prentice Hall，1973.

[2]王学平，屈小兵.连续并既约元及其在刻画Fuzzy关系方程解集中的应用[J].数学学报，2006，49（5）：1171-1180. WANG X P，QU X B.Continuous join-irreducible elements and their applications to describing the solution set of fuzzy relational equations [J].Acta Mathematica Sinica，2006，49（5）：1171-1180（in Chinese）.

[3]姜广浩，韩贵文，蔡锦.弱完全并既约元及其应用[J].模糊系统与数学，2012，26（2）：160-164. JIANGGH，HANGW，CAIJ.Weakcompletejoin-irreducibleelements and some applications[J].Fuzzy Systems and Mathematics，2012，26（2）：160-164（in Chinese）.

[4]BIRKHOFF G.Lattic Theory[M].3rd ed.New York：Amer Math Soc Colloq Public，1979.

[5]GIERZ G，KEIMEL K，SCOTT D S，et al.Continuous Lattices and Domains[M].Cambrige：Cambridge University Press，2003.

[6]马晶晶，卢涛，杜银玲，等.弱下邻及其性质[J].淮北师范大学学报：自然科学版，2013，34（3）：4-5. MA J J，LU T，DU Y L，et al.Weak adjoin and its properties in different conditions[J].Journal of Huaibei Normal University：Natural Science，2013，34（3）：4-5（in Chinese）.

[7]郑崇友，樊磊，崔宏斌.Frame与连续格[M].北京：首都师范大学出版社，2000. ZHENG C Y，FAN L，CUI H B.Frame and Continuous Lattices[M]. Beijing：Capital Normal University Press，2000（in Chinese）.

（责任编校 马新光）

Adjacent and weak adjacent

WANG Di，LU Tao
（School of Mathematical Science，Huaibei Normal University，Huaibei 235000，Anhui Province，China）

The concepts of weak complete intersection irreducible elements,co-dcpo and way-up are introduced.Then the concept of weak adjacent is given based on way-up and new auxiliary relation.Finally，the properties of adjacent and weak adjacent are discussed by using weak complete irreducible elements in semilattices，complete lattices and co-dcpo.

way-up；weak complete intersection irreducible elements；co-dcpo；weak adjacent；interpolation property

O153

A

1671-1114（2016）05-0017-03

2016-03-30

国家自然科学基金资助项目（11171156）；安徽省高校自然科学研究重点资助项目（KJ2015A064）.

王 娣（1991—），女，硕士研究生.

卢 涛（1974—），男，副教授,主要从事拓扑学和范畴论方面的研究.