水对岩质边坡倾倒变形影响的DDA模拟

张国新，雷峥琦，程 恒

（流域水循环模拟与调控国家重点实验室 中国水利水电科学研究院，北京 100038）

水对岩质边坡倾倒变形影响的DDA模拟

张国新，雷峥琦，程 恒

（流域水循环模拟与调控国家重点实验室 中国水利水电科学研究院，北京 100038）

大量工程实例表明，水位变动与水库库岸岩质边坡的变形失稳有紧密联系。本文基于非连续介质力学的DDA（Discontinous Deformation Analysis）方法，采用经典的Goodman倾倒模型，对边坡进行倾倒变形及失稳过程模拟，分析了岩质边坡倾倒变形的机理、影响因素，变形稳定和整体失稳的控制条件。在此基础上，考虑水的浮托力和渗透力的作用，模拟了水对岩质边坡倾倒变形的触发作用以及水位变动对变形的影响，分析了水对岩质边坡安全系数的影响。模拟结果显示，发生倾倒变形的安全系数远小于整体稳定安全系数；坡脚的稳定性对边坡的整体稳定起控制作用，坡脚的滑移是边坡发生倾倒变形的必要条件；水的作用降低了坡脚的稳定性，一定条件下是边坡进一步发生倾倒变形的触发因素。

岩质边坡；倾倒变形；水的作用；DDA方法

1 研究背景

地质灾害防治是水库大坝建成后的一个重要任务。国内外不乏水库蓄水后库岸发生滑坡造成灾害的例子。如建于意大利威尼斯省的瓦伊昂水库建成蓄水至正常水位3年后发生大滑坡，体积达2.4亿m3的巨型滑坡体滑入水库，引起超出坝顶高程100 m的巨浪，造成近2 600人死亡的惨痛灾难［1］。美国的大古力水电站建成后的头10年发生了近500次的库岸滑坡［2］。1961年我国湖南的拓溪水库蓄水初期近坝库区右岸塘岩光村165万m3大滑坡，引起的涌浪翻过坝顶，造成重大损失，死亡40人［3］。2003年7月三峡水库开始蓄水一个月后湖北秭归县沙镇溪镇千将坪村1 500万m3山体突然下滑，造成14人死亡、10人失踪，带来巨大经济损失。2007年水位自156m调节至151m后重庆万州发生滑坡6处，2008年175m蓄水试验以来，重庆段共发生滑坡150多处，直接经济损失超过5亿元［4］。

此外，有的滑坡体虽然尚未形成滑坡破坏，但在蓄水后启动滑动变形，长期处于蠕动变形状态，该变形与水位变化密切相关，存在发生大型滑坡灾害的风险。如清江隔河岩水库茅坪滑坡体，总体积2 350万m3，1993年4月水库蓄水后开始变形，截止2004年累计水平变形2 747.1mm，垂直位移548.4mm［5-6］。黄河某大型水电站蓄水后右岸边坡总体积达数千万立方米的滑坡体开始向河床蠕动变形，截至目前累计变形已达30多米，实属世界罕见［7］。

降雨和水库蓄水所引起的地下水位抬升是诱发滑坡的主要原因［8］。国内外很多学者研究了水对岸坡稳定的作用机理［9］，其影响主要体现在水作为浮托渗透力的作用和对岩体力学参数的影响两个方面。日本土木学会的调查结果显示，在水位上升和下降阶段，滑坡发生的比例分别为60%和40%［10］。在水位上升及稳定阶段，地下水对滑坡体产生浮托作用，从而减小了土体或岩体构造面的有效压应力，而在水位下降阶段，水主要以渗透力的方式增大滑坡体的下滑力。水对力学参数的影响是指，土体或岩体在水的浸泡之下发生软化，抗剪强度降低。这两种作用都会降低岸坡的稳定安全系数，诱发滑动变形，极端情况下导致滑坡破坏发生。

传统的边坡稳定性分析方法是极限平衡法［11］。土质边坡稳定分析以极限分析法为主，陈祖煜等做了大量深入的研究工作，开发了二维、三维稳定分析程序［12］。土体的极限分析方法中，以考虑水作用之后的有效应力作为条块之间的相互作用力进行计算。然而在进行岩石的极限分析时，考虑水作用的难度较大。熊将等［13］通过在块体的底面和侧面考虑水的浮托力，对岩质边坡稳定计算的Sarma法进行了改进，并应用于库岸边坡的稳定计算。有限元类的数值方法可以将水的作用作为渗透力在计算中予以考虑，但对于主要受结构面影响的岩质边坡稳定计算，有限元等连续类方法难以给出理想的结果。

石根华提出的非连续变形分析［14］以被天然节理裂隙切割的任意块体为基本单元，以单元的刚体位移和变形为未知量，考虑块体间的相互作用，通过最小势能原理建立方程，采用隐式解法求解。张国新等［15］对石根华的DDA程序进行了二次开发，增加了渗流-变形耦合功能，以界面渗透力的方式考虑水的作用。本文基于经典的Goodman倾倒模型，采用扩展的DDA方法模拟研究了水位变动对块体间有效应力、单个块体安全度及边坡整体稳定性的影响，进而揭示了考虑水作用的倾倒变形机理及失稳滑动机理。

2 基于DDA的渗流-变形耦合

2.1 裂隙渗流模拟 裂隙水以水头压力的方式作用于岩体，引起含裂隙岩体的变形，岩体变形后，结构面的几何参数发生变化，又反过来影响水在裂隙中的流动。因此，裂隙水的运动和裂隙岩体的变形是一种耦合作用。

完整岩石的渗透系数非常小，水主要通过岩石中的裂隙流动。因此本文采用离散裂隙网络模型模拟裂隙岩体的渗流，忽略岩块的透水性。首先将实际勘测的节理、裂隙等结构面进行任意切割，得到岩体裂隙网络，然后用逐个检查删除法或拓扑分析方法，删除水力不连通的裂隙单元，将裂隙网络变为渗流网络［16］，最后在渗流网络上施加边界条件，通过水力学有限元分析，求得各结点处的水头。

本文假定沿裂隙的平均渗流流速满足广义达西定律，其表达式为：

式中：i为水力梯度；K为裂隙中的水力传导系数；α为与水力分区有关的经验系数，根据Louis的试验［17］，K和α可以由表1中的公式求得。

表1 不同分区的水力传导系数K和经验系数α的取值

因此，通过任一裂隙单元的流量即为：

式中：Δh为裂隙两端点的水头差，b为裂隙开度，l为裂隙长度。

由表1可以看出，当裂隙内渗流流态为层流时，该式即为著名的渗流立方定律，此时系数p与水头差无关，当流态为紊流时p与Δh相关。

对于整个裂隙网络，根据式（2）可以得出以节点水头为未知量的整体方程：

裂隙的变形对岩体渗流场会产生重大影响，其主要表现为裂隙隙宽b的改变。本文中裂隙隙宽的计算基于以下假定［13］：

（1）裂隙闭合后，仍存在机械隙宽δ1及过流面积系数S。机械隙宽δ1为缝面法向压力的函数：

式中：σn为缝面的法向压力，压为正，δ0为当缝面法向压力为零时的隙宽，n为系数。δ0和n均由实验确定。虽然过流面积系数S也与法向压力有关，随法向压力的增大而减少。但现有实验结果表明，即使在很高的法向压力下，裂隙的接触面积仍不超过总面积的15%，故本文假定S为一常数。

（2）当裂隙张开后，总的平均隙宽b为法向应力为零时的残余隙宽δ0与裂缝张开宽度δ2的加权平均，即b=Sδ0+δ2。

2.2 基于DDA的变形分析 非连续变形分析DDA的主要研究对象是被节理、裂隙、断层等构造切割而成的块体系统。每一个块体即一个单元，单元的形状可以任意，单元的几何形心为分析的代表点（如图1），以形心的刚体位移（包括线位移和角位移）、单元的线应变和切应变为基本未知量（见式（5）），单元内任一点的位移可通过插值函数（见式（6））求得。

式中：u0、v0、r0分别为单元形心的线位移和角位移；εx、εy、γxy分别为单元的线应变和切应变；u、 v为单元内任一点的位移；为插值函数。

当单元之间相互接触时，在接触点设置弹簧以保证接触点的位移协调。综合考虑变形能、动能、弹簧接触能等外力功能以及块体系统的总能量，采用最小势能原理可构造出块体系统的整体平衡方程：

求解式（7）得出各时刻块体形心的位移和应变，进而可求出全部的位移场、应力场、接触弹簧的变形及接触力。

原有的DDA程序中，未考虑水压荷载，本文基于能量原理推导考虑裂隙渗流时的平衡方程。如图2所示，设单元i的第k条边上作用有线性分布的水头荷载，其两端的水头值分别为hk，hk+1。此时，两端压力在x、y方向的分力分别为：

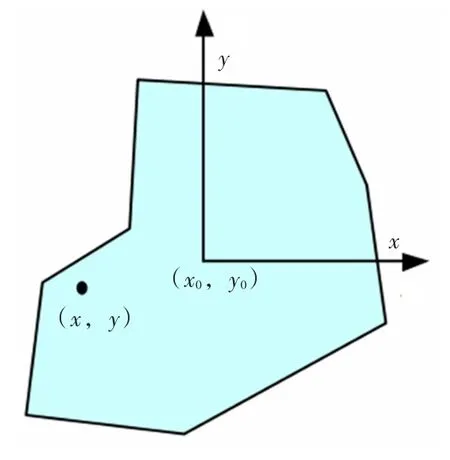
图1 DDA的单元定义

图2 DDA单元上的水荷载

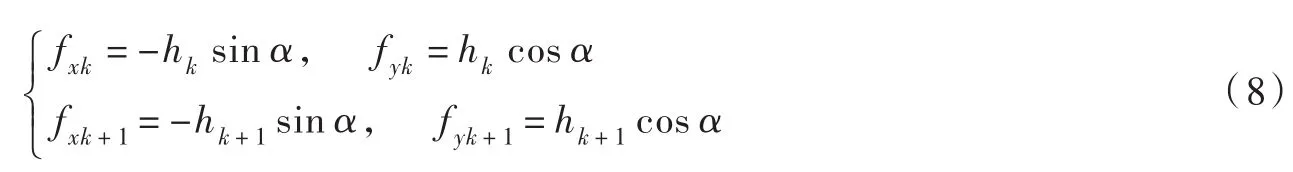
则水压力在单元i上作的功为：

式中，lk为第k条边的长度，［E］、［G］分别为：

由水头压力引起的单元i的节点荷载为：

用式（10）、式（11）求出水压荷载并代入式（7），就得到了考虑裂隙渗流的DDA瞬时平衡方程。为了便于计算，在保证计算精度的前提下，本文采用了渗流与变形的弱耦合模型［18］，即每个计算时步求得的裂隙开度为下一时步进行渗流分析的输入参数，同一时步内不再进行渗流-变形的迭代计算。计算流程见图3：

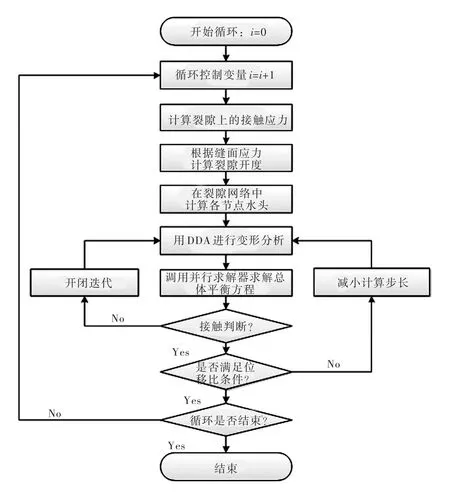
图3 考虑裂隙渗流的DDA模拟流程图

3 岩质边坡倾倒变形机理分析

Goodman等［19］根据刚体极限平衡原理提出了不计接触面黏聚力的倾倒失稳分析方法（简称G-B法），该方法可以分析被顺坡和陡倾逆坡构造面切割而成的边坡的倾倒破坏，并能求出各块体的失稳状态。孙东亚等［20］和何传永等［21］等将DDA方法应用于岩质边坡的倾倒变形分析，并与G-B法进行比较，验证了DDA的有效性。因此本文不再对DDA的有效性进行论证。

本节利用文献［19］中介绍的模型，采用DDA方法模拟岩质边坡的倾倒变形，进一步揭示其机理和启动条件（见图4）。如图4所示，模型长215m，高125m，被分割成16个块体，沿坡脚向上依次编为1至16号，底滑面的坡度为30°，在坡脚和坡顶分别设置观测点A、B。分析中采用的基本参数为：重度2.5t/m3，泊松比0.25，块体间接触面的黏聚力取0，陡倾坡内的构造面摩擦角固定为25°，设顺坡向构造面的摩擦角为φ，计算当φ取不同值时，边坡块体的变形特性及失稳模式。计算中关注如下几个问题：（1）取不同φ角时，边坡的变形过程和失稳模式；（2）使边坡整体保持稳定的临界稳定摩擦角；（3）使边坡整体不发生倾倒变形的临界摩擦角。

图4 DDA计算模型

3.1 无倾倒变形时的受力分析 将顺坡构造面的摩擦角φ取一个较大值，即不允许块体沿坡发生滑动，计算得到的块体及各接触面的受力见图5及表2。

图5 不允许顺坡滑动时的应力分布

由图5及表2可见，在自重作用下，上部块体对下部块体施加挤压作用。沿边坡从上到下，块体底部的法向应力与块高成正比，呈中部大，两端小的分布。顺坡向剪应力则呈中下部大，上部小的分布，由16号块底面的0.06MPa逐步增大到8号块的0.34MPa，随后又减小至3号块的0.25MPa，最后又增大至1号块底面的0.35 MPa。块体与块体之间通过顶、底部接触点传力，16—14号块体之间的作用力为张拉作用，12—1号块之间为挤压作用。块体间的挤压应力由上向下逐步增大，由14—13号块之间的0.04 MPa增大到2—1号块体之间的1.52 MPa。

由图5看出，虽然各块体没有沿坡向的滑移，但14-13号块之间出现了张开变形，边坡上部表现出小量的倾倒变形特征。该变形来自于1—13号块之间挤压变形的累积，在底部块体不出现下滑的条件下，这种倾倒变形很小，本文算例仅为0.8m。

取不同的顺坡向构造面摩擦角进行计算，表3为各块体底面的抗滑稳定安全系数。由表3可见，16—14号块体不受倾倒变形的影响，为自平衡块体，安全系数相等。从13号块体沿坡面向下，块体的安全系数逐渐降低，1号块体的安全系数最低，仅为2号块的1/2，所以算例中的典型边坡很容易因下部块体的滑移引起整体倾倒变形。

3.2 不同摩擦角时的变形模式及稳定性 允许块体滑动，顺坡向构造面取不同的摩擦角，用DDA计算相应的倾倒变形模式及变形量。图6为不同φ角时的最终变形示意图，表4给出了不同φ值时各块体的位移和变形模式。根据计算结果，当φ角小于61°时，1号块发生滑动，为上部各块的变形提供空间，边坡开始出现倾倒变形，各块的变形模式和变形量取决于φ角。自下往上各块的变形模式分别为滑动、滑动加倾倒、倾倒和稳定。随着φ角降低，下部滑动块增多，滑动加倾倒的块数增多。当φ大于30°时，14—16号块体始终保持稳定，不同块体的变形值与φ角相关，φ角越小，变形越大。当φ大于36°时变形由下向上逐步变大，即下部的滑移变形被上部块体的倾倒变形放大，放大倍数取决于块体的高度和φ角。当φ在30°～36°之间时，由于下部为滑动及滑动加倾倒而上部只有倾倒，下部变形大于上部。当φ小于30°，即φ小于坡脚时，上下部处于同步变形状态，呈失稳型主动下滑及倾倒变形。综上所述，当φ角小于坡角时将发生整体失稳；当φ角大于坡角时，边坡可能发生倾倒变形，但整体最终能保持稳定，这也是某些较大规模的倾倒变形岩质边坡仍能发生失稳的原因。

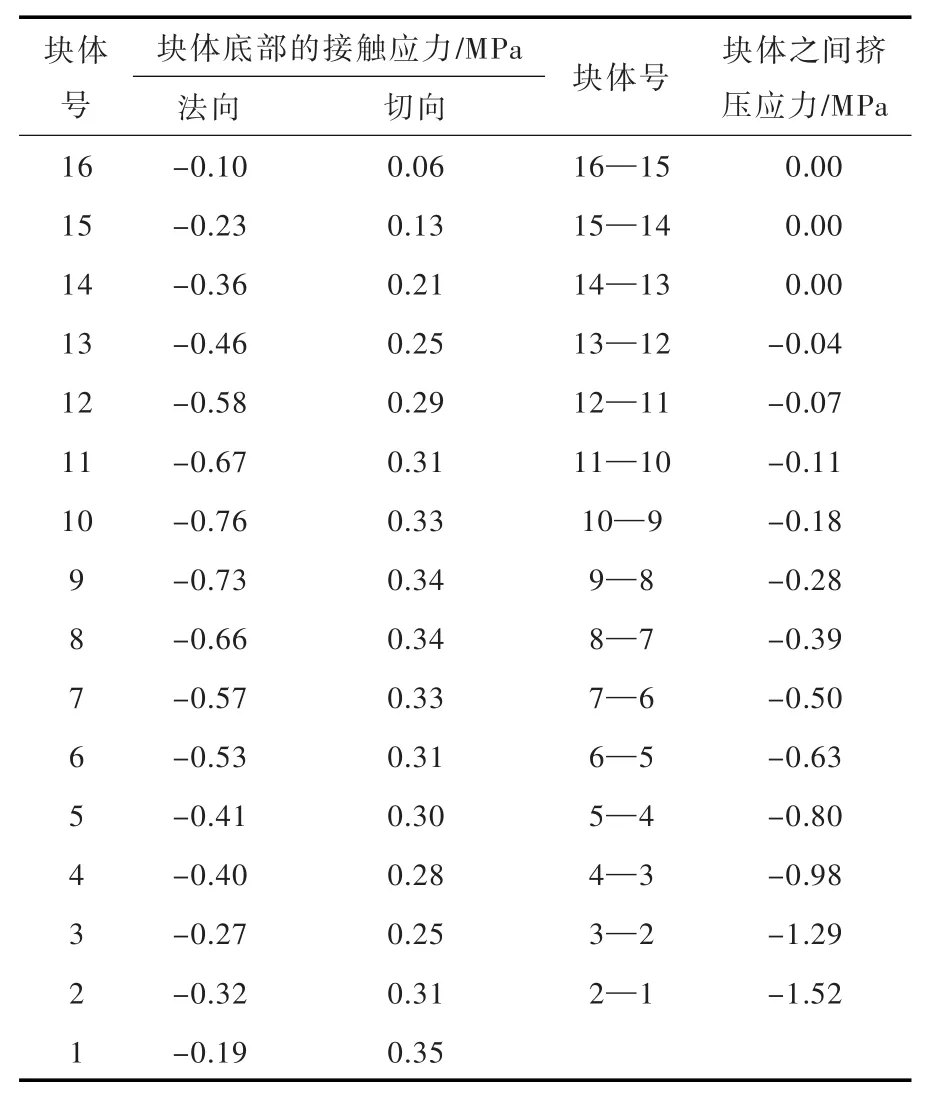
表2 不允许顺坡滑动时的块体间作用力

表3 不同摩擦角时各块体底滑面安全系数

图6 不同摩擦角时的倾倒模式

模拟结果表明，岩质边坡的倾倒变形来自于下部块体的滑移和块体自身变形的累积。当边坡下部构造面强度足够高时，块体不发生滑移，边坡少量的倾倒变形主要来自于各块体自身变形的累积，而较大的倾倒变形量必然伴随有下部块体的滑移。又由于受到自上向下的挤压作用，边坡下部块体底面的剪应力很大，一旦超过构造面的抗剪强度，很容易引发大的倾倒变形。此外，边坡的整体稳定性取决于沿边坡的极限承载能力。

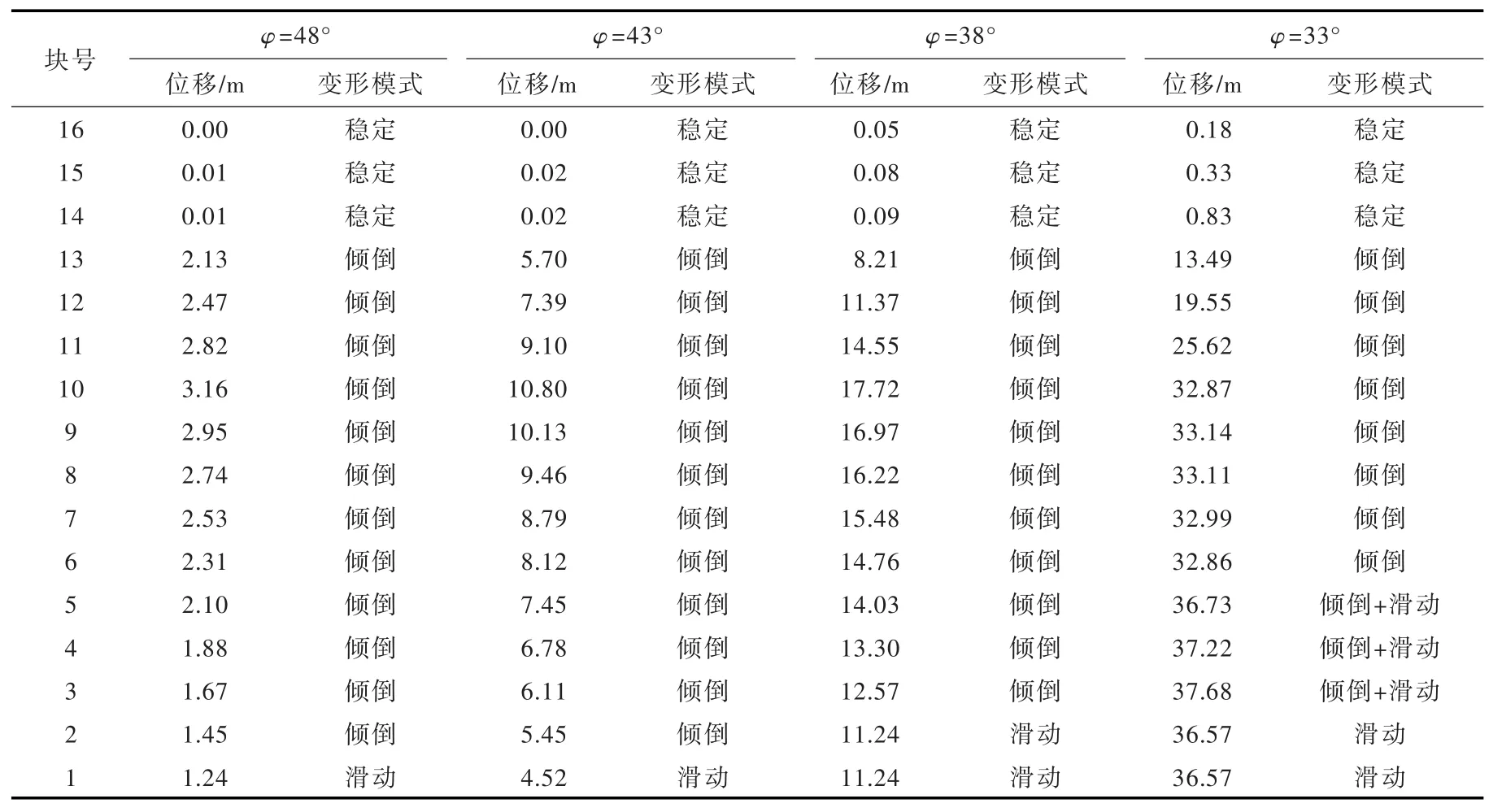
表4 不同φ角时各块体的位移和变形模式

4 水对岩质边坡倾倒变形与稳定的影响

水位变动往往是边坡变形和失稳的诱因。水的作用表现为两个方面：（1）以面力和渗流荷载的形式作用于边坡，使边坡岩体的受力条件发生变化；（2）长期浸泡使岩体的力学性质发生变化。水的作用会使已经处于变形稳定状态的边坡重新启动变形，或使本已处于稳定临界状态的边坡失稳。本节采用同上节相同的模型，用扩展的DDA程序，考虑裂隙岩体中渗流与变形的耦合作用，研究水对边坡倾倒变形和稳定的影响。

4.1 水对块体抗滑稳定安全系数的影响 取足够大的顺坡向摩擦角，在自重作用下计算稳定后，抬升水位至45.41 m，使1号块体被水淹没，用DDA方法求出各块体底面的法向与切向接触力。重复以上步骤，求出不同摩擦角时各块体的安全系数（见表5）。对比表3和表5可以看出：（1）水位抬升后，泡水块体底面的法向和切向应力均有所减小，但法向应力减小比例大于剪应力。（2）水位抬升后，16—3号块体底面的安全系数没有变化，1—2号块体的安全系数有所降低，1号块安全系数降低幅度为11%。（3）1号块发生滑动进而引起边坡倾倒变形的临界摩擦角由未泡水时的61.8°增大为64.5°。

4.2 水对边坡变形与稳定的影响 取不同的φ角，在自重作用下计算稳定后抬升水位至56.41m，模拟各块体的变形，A、B两个观测点的位移时程曲线见图7。

对于1号滑块，当底滑面的内摩擦角φ大于65°时水位抬升不会引起新的变形，当φ小于65°时水位抬升后会出现下滑，滑移量随φ角的减小而增大。当φ角等于50°时滑移量为1.34m，φ角等于42°时可达6.63m。坡顶处B点的变形规律与A类似，变形量随φ角的减小而增大。当边坡下部滑移较小时，B点处变形大于A点，即边坡上部对下部变形有放大作用。例如φ角为50°、45°时，B、A点处变形量的比值分别为2.91、4.55。

4.3 水位变动对边坡变形与稳定的影响 同上节，取不同的φ角，当自重作用下变形稳定后分级抬升水位至56.41、59.41和62.41m，观测点A、B的位移时程曲线如图8所示。

由图8可知，每次抬升水位都会触发新的变形，使下部块发生滑移，上部块发生倾倒。每次提高水位的基本变形规律与第一次相同，当φ角较大时上部变形大于下部，而φ角较小时，下部变形大于上部。

表5 水位抬升至45.41m时的接触力及安全系数

图7 水位抬升前后观测点的位移时程曲线

图8 分级抬升水位时观测点的位移时程曲线

4.4 水对倾倒变形影响的机理分析 天然边坡经受长年累月的自然作用，经历了充分的变形和调整，历史上在各种极端条件的作用下，目前大多处于临界稳定状态，通常状况下有一定的稳定安全度。当这些边坡遭遇工程措施，如开挖、水位变动等扰动，可能会打破原有的稳定状态，导致变形再次启动，甚至发生失稳。

水库建成蓄水后，库区中原本位于水面以上的部分库岸将被库水淹没，削落带范围内的库岸则需经受水位的周期性变化。岩质边坡常含有大量的节理裂隙等构造，透水性较好，因此水下的岩体要受到水的浮力作用。前述计算模型中的1号块体淹没前后受力如图9所示，图中：G为重力，N、T为遇水前沿滑裂面的法向、切向力，P为2号块对1号块的作用力，N′、T′、P′为考虑水作用后的法向、切向力及2号块对1号块的作用力。渗流产生的浮托力会减小滑面上的法向力和切向力，对于倾角α小于45°的顺坡构造，水的浮托力引起的法向应力减小量大于剪应力减小量。此外，1号岩块所受剪力主要来自上部岩块的挤压作用，因此浮托力引起的1号块体底滑面法向力减小比例远大于切向力，从而降低了水下滑块的安全系数，引起下部块体滑移为上部岩块的倾倒变形提供空间，最终引发边坡的整体倾倒变形甚至失稳破坏。

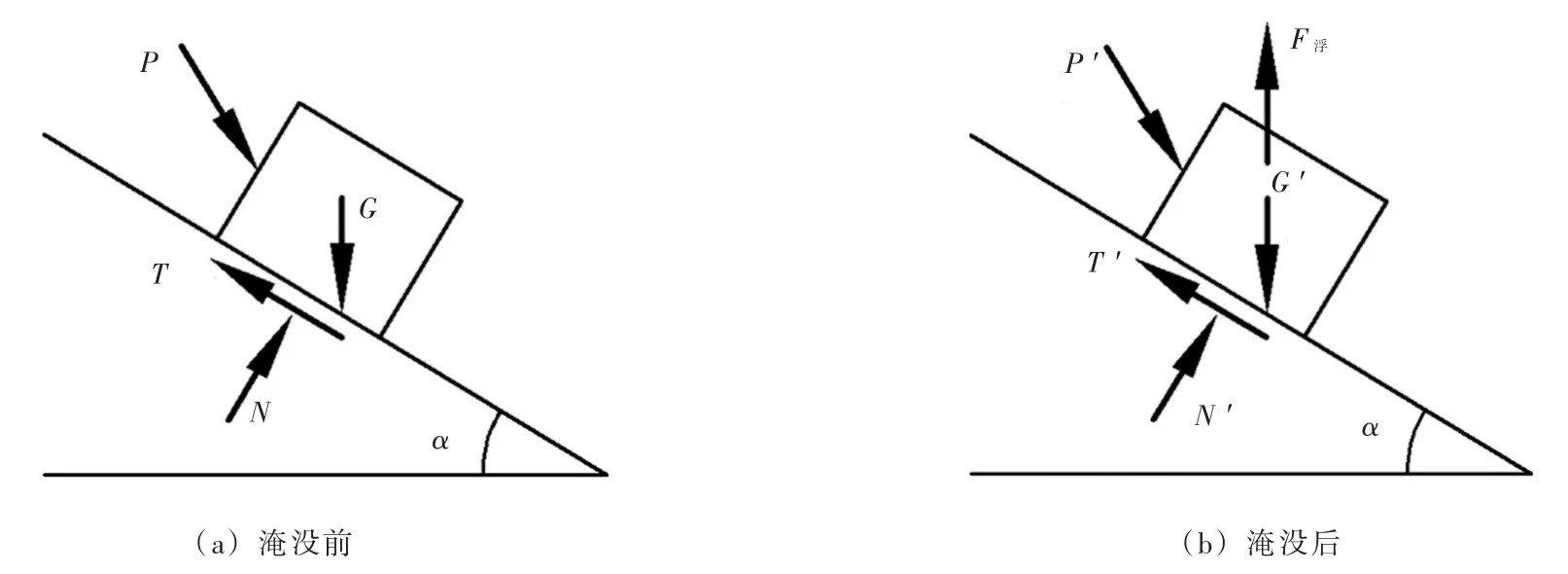
图9 1号岩块的受力分析

5 结论

本文利用Goodman-Bray的经典倾倒变形分析模型，考虑裂隙岩体的渗流-变形耦合作用，以数值模拟方式研究了岩质边坡倾倒变形的机理、启动条件和整体稳定条件。在此基础上，进一步研究了水位变动对岩质边坡倾倒变形的触发作用。通过以上模拟分析，得出以下几点结论：（1）在发生倾倒变形的岩质边坡中，上部岩体的倾倒变形来自于下部岩体的挤压或滑动变形，下部岩块的滑动为上部岩体的变形提供了空间，是上部岩体发生倾倒变形的必要条件之一；（2）倾倒变形带来的自上而下的挤压作用使下部岩块的抗滑稳定安全系数远小于上部，因此下部岩块发生滑动并带动上部岩块发生倾倒变形的临界摩擦角远大于滑面的倾角；（3）当岩体顺坡向构造面的摩擦角大于滑面倾角时，即使边坡发生倾倒变形，在下部岩块下滑一定距离后，上部岩体向下挤作用逐步释放减小，边坡最终仍能保持稳定。一般情况下倾倒变形的变形量自下而上逐渐放大，至边坡坡度变化的顶部达到最大，变形放大的倍数取决于块体高度和构造面的摩擦角；（4）对于发生倾倒变形并达到稳定状态的岩质边坡，坡脚受到扰动往往会诱发倾倒变形重新启动，这些扰动包括开挖及蓄水引起的水位抬升等；（5）当水淹没坡脚，下部块体浸入水中，水的浮力作用会减小块体与滑动面之间的法向力和剪切力，但对法向力的减小比例要远大于剪切力，因此会降低下部块体的抗滑稳定安全系数，使原处于变形临界状态的边坡开始倾倒变形；（6）分期蓄水时，每次抬升水位都会触发新的倾倒变形，但只要边坡能满足整体极限平衡条件，变形最终都能收敛。

［1］ 钟立勋.意大利瓦伊昂水库滑坡事件的启示［J］.中国地质灾害与防治学报，1994，5（2）：77-84.

［2］ 蔡耀军，崔政权，R.Cojean.水库诱发岸坡变形失稳的机理［C］//第六次全国岩石力学与工程学会大会论文集.北京：中国科学技术出版社，2000.

［3］ 肖诗荣，刘德富，胡志宇.世界三大典型水库型顺层岩质滑坡工程地质比较研究［J］.工程地质学报，2010，18（1）：52-59.

［4］ 乔建平.长江三峡库区蓄水后滑坡危险性预测研究［M］.北京：科学出版社，2012.

［5］ 严福章，王思敬，徐瑞春.清江隔河岩水库蓄水后茅坪滑坡的变形机理及其发展趋势研究［J］.工程地质学报，2003，11（1）：15-24.

［6］ 李守定，李晓，刘艳辉.清江茅坪滑坡形成演化研究［J］.岩石力学与工程学报，2006，25（2）：377-384.

［7］ 张海平.黄河拉西瓦水电站果卜岸坡稳定性预测及失稳预报研究［D］.成都：成都理工大学，2011.

［8］ 王宇，李晓，等.降雨作用下滑坡渐进破坏动态演化研究［J］.水利学报，2013，44（4）：416-425.

［9］ 黄润秋.20世纪以来中国的大型滑坡及其发生机制［J］.岩石力学与工程学报，2007，26（3）：433-454.

［10］ 日本土木学会.岩盤斜面の調査と対策［M］.丸善（株）発売，1999.

［11］ 王吉亮，李会中，等 .乌东德水电站右岸引水洞进口边坡稳定性研究［J］.水利学报，2012，43（11）：1271-1278.

［12］ 陈祖煜，等.土质边坡稳定分析［M］.北京：中国水利水电出版社，2003.

［13］ 熊将，王涛，盛谦.库区边坡稳定性计算的改进Sarma法［J］.岩土力学，2006，27（2）：323-326.

［14］ 石根华.数值流行法与非连续变形分析［M］.裴觉民，译.北京：清华大学出版社，1997.

［15］ 张国新，武晓峰.裂隙渗流对岩石边坡稳定的影响-渗流、变形耦合作用的DDA法［J］.岩石力学与工程学报，2003，22（8）：1269-1275.

［16］ 张有天.岩石水力学与工程［M］.北京：中国水利水电出版社，2005.

［17］ Louis C A.A study of groundwater flow in jointed rock and its influence on the stability of rock mass［J］.Rock Mechanics Research Report，1969（10）：10-15.

［18］ ZHANG GuoXin，Li Xu，Li HaiFeng.Simulation of hydraulic fracture utilizing numerical manifold method［J］. Technological Sciences，2015，58（9）：1542-1557.

［19］ Goodman R E，Brayjw.Toppling of Rock Slopes［C］.Proceeding of the Specialty Conference on Rock Engineering for Foundations and Slopes.Colorado，1976：201-234.

［20］ 孙东亚，彭一江，王兴珍.DDA数值方法在岩质边坡倾倒破坏分析中的应用［J］.岩石力学与工程学报，2002，21（1）：39-42.

［21］ 何传永，孙平，吴永平，等.用DDA方法验证倾倒边坡变形的制动机制［J］.中国水利水电科学研究院学报，2013，11（2）：107-111.

DDA simulation of impact of water on toppling deform ation of rock slope

ZHANG Guoxin，LEI Zhengqi，CHENG Heng
（State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin，China Institute of Water Resources and Hydro power Research，Beijing 100038，China）

A large number of engineering examples show that water storing and changes in water level are closely related to the failure of rock slopes in a reservoir.Based on DDA method of the non-continuum mechanics，the failure process is simulated.Mechanism，influences and instability of toppling deformation of the rock slope are analyzed.On this basis，considering the uplift and penetration of water，the trigger effect of water on toppling deformation is simulated.The simulation obviously proves the relationship between water changes and deformation.The water could influence the safety factor along the sliding surface.The result shows that the safety factor of topp ling deformation is much lower than that of stability.The stability of the slope toe is the key factor to the stability of the whole rock slope.The slip of the slope toe is necessary condition of the slope failure.Water effect reduced the stability of the slope toe.It is the trigger factor for the topp ling deformation under a certain condition.

rock slope；toppling deformation；water effect；DDA method

TV413.6

A

10.13244/j.cnki.jiwhr.2016.03.001

1672-3031（2016）03-0161-10

（责任编辑：李 琳）

2016-01-13

国家自然科学基金面上项目（51579252）；国家自然科学基金重点基金项目（51439005）；流域水循环模拟与调控国家重点实验室自主研究课题（2015TS05）

张国新（1960-），男，山东临朐人，博士，教授级高级工程师，主要从事结构应力分析及数值方法研究。E-mail：gx-zhang@iwhr.com