基于HyperWorks软件的单轨道岔梁结构优化方案

谭 珊 王智祥

(1.长江大学工程技术学院，434020,荆州; 2.重庆交通大学机电与汽车工程学院，400074,重庆∥第一作者,助教)



基于HyperWorks软件的单轨道岔梁结构优化方案

谭 珊1王智祥2

(1.长江大学工程技术学院，434020,荆州; 2.重庆交通大学机电与汽车工程学院，400074,重庆∥第一作者,助教)

以重庆轨道集团委托川东船厂制造的单轨道岔梁为例,利用有限元分析软件HyperWorks对道岔梁的结构进行了静强度分析。静强度分析的结果表明,梁体强度完全满足使用要求,但材料存大较大的浪费。在保证承载力及必要安全裕度的前提下,利用HyperWorks软件中的OptiStruct模块对道岔梁进行了拓扑优化和进一步的尺寸优化。优化后,梁体质量降低了18.4%,优化效果明显。

单轨; 道岔梁; 数学模型; 拓扑优化; 尺寸优化

First-author′s address College of Technology & Engineering, Yangtze University,434020,Jingzhou,China

道岔是轨道交通系统中非常重要的组成部分。道岔的基本型式有单开、对开、三开和五开道岔等,本研究涉及的道岔为五开道岔。重庆轨道交通集团委托川东造船厂生产的单轨交通道岔梁,是由钢板焊接而成的箱形结构件,通过对道岔梁进行静强度分析发现,梁体强度完全满足承载力要求,但材料却存在极大的浪费。在保证梁的承载力及必要安全裕度的前提下,本文在静强度分析的基础上,利用有限元分析软件HyperWorks的优化功能对道岔梁进行了结构优化设计,降低了结构质量,减少了工作量,节约了制造成本。

1 道岔梁的静强度分析

1.1 有限元模型的建立

该道岔梁总长30 m,共分成5个梁段,每段6 m,安装在两条线路的特定位置。通过每个梁段下部的台车来移动道岔梁至一定角度,达到列车变更轨道的目的。3#道岔梁是由204块钢板焊接而成,为箱形截面,由顶板、底板、横隔板、腹板、导向和稳定面板,以及一些横向、纵向支撑构件组成。箱梁计算跨径6 m,梁高1.42 m、宽0.85 m,顶板厚14 mm,底板厚16 mm,腹板厚10 mm,导向和稳定面板厚12 mm。每跨道岔梁内设7道横隔板,横隔板间距均为0.7 m。除梁段间起联接作用的部件为合金材料外,梁的主体全部使用Q235-B材料。

本模型网格单元采用四结点壳单元进行划分,单元尺寸为25 mm,共建立了81 593个单元,80 456个节点。弹性模量E=2.1×105N/mm2,剪切模量G=8.1×104MPa,泊松比ν=0.3。道岔梁的三维有限元模型见图1。

1.2 载荷及边界条件

1.2.1 载荷条件

根据列车的实际受力情况,考虑如下几种荷载:

(1) 恒荷载。道岔梁质量M=4.225 t。

(2) 列车竖向静力荷载。取列车单轴标准荷载P1=110 kN,由于列车荷载属于活荷载,计算时考虑动力冲击影响。根据《跨坐式单轨交通设计规范》,动力冲击系数取为1+μ=1.36。故列车静力荷载为P2=1.36P1=149.6 kN。

(3) 列车横向荷载。列车在转线时,道岔梁不可能保持绝对的平直,列车存在横摆现象,所以列车在行驶过程中车体对道岔梁还具有垂直行驶方向的横向作用力,且其直接作用在轮胎与轨道梁的接触点上。根据《跨坐式单轨交通设计规范》,列车横向载荷N=P1×0.25=27.5 kN。

(5) 列车制动力及牵引力。轨道列车的制动力P3按列车单轴标准荷载的25%计算,P3=P1×25%=27.5 kN。

即考虑的荷载组合为:恒载+列车竖向静力荷载+列车横向荷载+风载荷+列车制动力。

1.2.2 边界条件

根据道岔梁的实际安装位置,将约束设定在道岔梁左右两端截面上,共约束了X、Y、Z三个方向的平动自由度和绕X、Y方向的转动自由度,仅放开绕Z轴方向的转动自由度。

1.3 静强度分析结果

通过计算，得到梁体的静强度分析结果如表1所示。

表1 静强度分析结果

3#梁的最大应力σmax=68.37 MPa,考虑安全系数q(q取1.5),则σmax×q=102.56 MPa,小于材料屈服应力235 MPa,也小于轴向允许应力135 MPa。其最大位移为0.425 5 mm,变形量非常小,小于《跨坐式单轨交通设计规范》中7.1.8条规定的最大位移容许值l/800=7.5 mm(式中l为道岔梁的跨度)。因此，3#梁梁体的强度和刚度完全满足使用要求,结构存在比较大的优化余地。

2 基于OptiStruct的结构优化设计

2.1 拓扑优化

2.1.1 拓扑优化的数学模型

道岔梁不仅直接承受车辆的载荷,在车辆转向时还需要与轨道梁进行良好对接,考虑到道岔梁实际运行过程中的实用性和合理性,设计区域定义为梁体内部横隔板及内部横向、纵向构件,其余区域包括顶板、底板、腹板、导向和稳定面板为非设计区域。在本项目中,设计变量为设计域内每个单元的相对密度,以体积分数不大于0.3为约束条件,目标函数为结构整体的柔度最小化。本次道岔梁结构拓扑优化的数学模型为:

求X={x1,x2,…,xn}T

式中：

xi——设计变量,即每个微单元的相对密度，i=1，2，…，n;

C——结构的柔度,即应变能;

F——载荷矢量;

U——位移矢量;

k——材料百分比;

V——优化后材料的体积;

V0——设计区域体积;

K——整体刚度矩阵。

2.1.2 拓扑优化的计算

在拓扑优化参数设置完毕后,将数据提交到OptiStruct模块中进行计算。经过10次迭代后,计算过程终止。优化后的单元密度云图如图2所示。

图2 设计区域密度云图

针对拓扑优化的结果,分别对各部件优化结果进行详细分析。梁体内部横隔板密度靠近1的区域非常大,越靠近梁体中部,密度为1的区域越多,说明横隔板为内部重要受力构件,大部分需要保留。内部横向构件中有部分密度接近1,但也有相当一部分密度为0,并不参与受力变形,属于可以去掉的部分。纵向构件大部分区域密度为0,只有极少数靠近中部区域密度为1,说明纵向构件可删除的材料非常多,有比较大的优化余地。

2.1.3 拓扑优化设计方案

横隔板的形状和分布位置不做改变,与优化前相同;横向构件共36块,只保留靠近中部的部分构件,与下板相接的横向构件全部去除,共删除构件24块;纵向构件共4块板,下部2块全部去除,只保留上部2块,且其长度由原来的6 000mm缩短到

1 400mm。具体的拓扑优化方案如图3所示。优化后的应力和位移云图如图4所示，其参数对比如表2所示。

图3 优化方案示意图

图4 优化后的应力和位移云图

项目最大应力值/MPa最大位移值/mm质量/t优化前68.30.4264.703优化后66.50.4354.229

由表2可见，优化后结构的最大应力为66.5 MPa,最大位移为0.435 mm,梁质量减轻了0.474 t,下降比例为10.07%,优化效果明显,且最大应力值较优化前有略微下降、分布合理。

2.2 拓扑优化基础上的再优化

2.2.1 隔板的再设计

拓扑优化方案是在原结构的基础上删除了部分内部构件,而内部的横隔板未做改变。为了找到横隔板的最佳材料分布,重新建立了横隔板的优化模型。定义体积分数和柔度作为响应函数,约束体积分数不超过0.5,目标函数为结构整体的柔度最小。通过拓扑优化计算得到了横隔板的优化方案,如图5所示。

2.2.2 尺寸优化

为进一步降低结构质量,在拓扑优化方案和隔板再设计的基础上，对结构做进一步的尺寸优化。

图5 横隔板优化方案

2.2.2.1 设计变量

综合考虑道岔梁的结构形式,选取梁体顶板、底板、腹板、横隔板、导向和稳定面板、横向构件、纵向构件的厚度作为优化设计变量,共7个设计变量。受压板件的局部稳定性与板厚密切相关,因此将设计变量与壳单元的厚度属性相关联,以此来确保受压板件的局部稳定性。道岔梁中部横剖面图如图6所示。

将优化变量写成矩阵形式:

X= [x1,x2,x3,x4,x5,x6,x7]=

[b1,b2,b3,b4,b5,b6,b7]

式中:

b1——顶板厚度;

b2——底板厚度;

b3——腹板厚度;

b4——横隔板厚度;

b5——导向和稳定面板的厚度;

b6——内部横向构件厚度;

b7——内部纵向构件厚度。

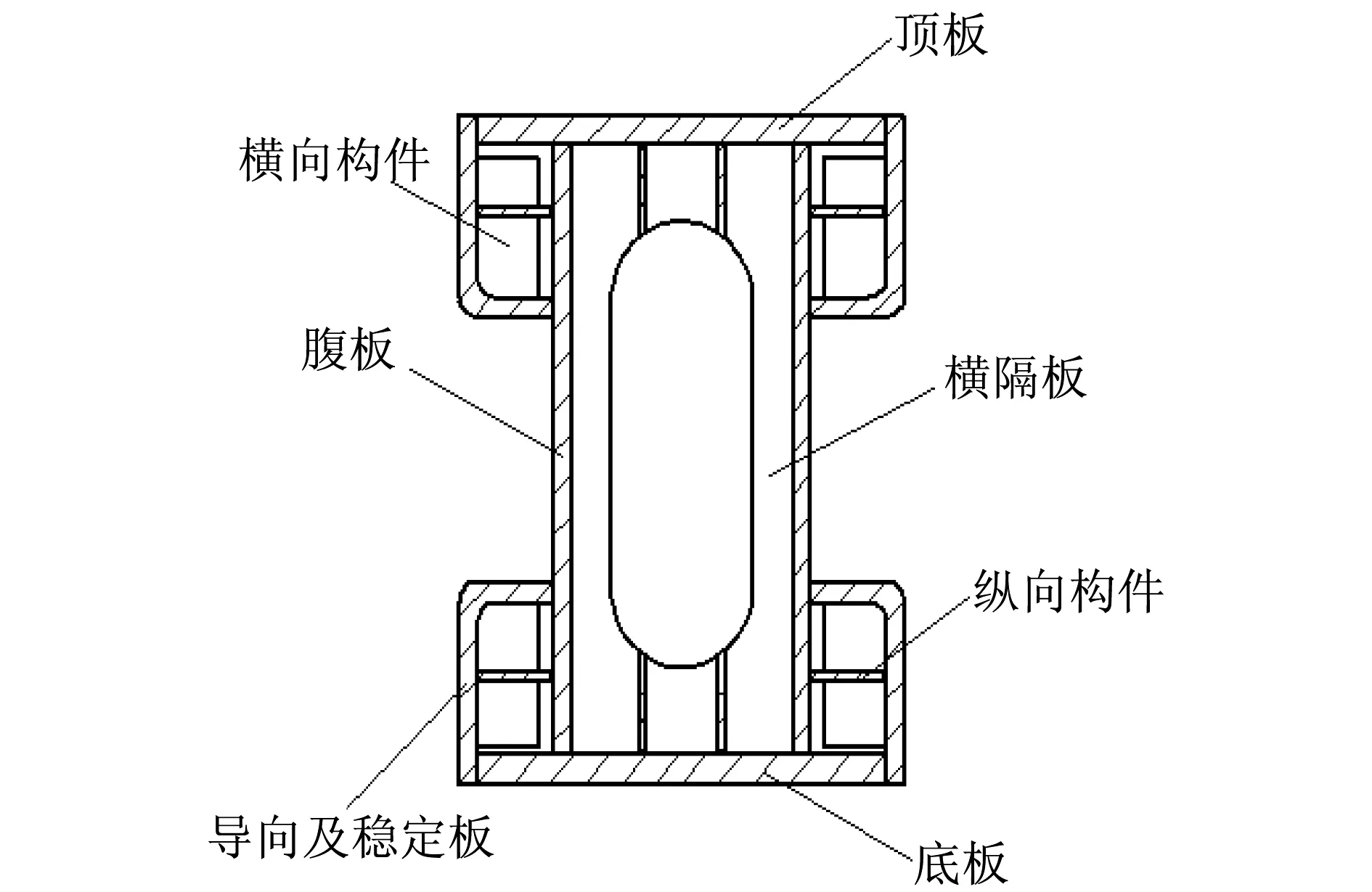
图6 道岔梁中部横截面图

根据重庆市轨道交通集团的要求,为满足施工安全及工艺要求,板厚的变化值不得大于板厚的20%,即小于等于2 mm(即10 mm×20%),则设计变量及取值范围如表3。

表3 设计变量及取值

2.2.2.2 约束条件

应力约束条件:最大应力与优化前相当,不能超过70 MPa,即σmax≤70 MPa。

位移约束条件:为保证安全,要求在工作状态下梁的总位移不能超过设计值,根据《钢结构设计规范》的规定,限定道岔梁的最大位移不能超过3 mm。2.2.2.3 目标函数

目标函数为结构质量最轻,即：M=6 000ρ1×(850x1+850x2+2 780x3+436.3x4+2 404x5+382.75x6+586x7)为最小(式中ρ1为材料密度)。

道岔梁尺寸优化的数学模型为:

求X={x1,x2,x3,x4,x5,x6,x7}T

式中：

xi——每块板的厚度，i=1，2，…，7；

M——道岔梁的总质量；

σmax——最大正应力；

dmax——梁总体最大位移。

2.2.2.4 尺寸优化计算结果

经过3次迭代后,计算过程结束,得到的尺寸优化结果见表4,应力、位移云图如图7、图8所示。尺寸优化前后的参数如表5所示。

表4 尺寸优化结果

在拓扑优化基础上做进一步尺寸优化后,结构质量下降至3.83 t,最大应力为70 MPa,最大位移为0.567 mm,在合理范围之内,满足道岔梁强度、刚度及稳定性要求；通过验算,各板件的局部稳定性也满足要求,说明此次优化方案可行有效。与优化前数据对比发现,尺寸优化后梁体质量再次减轻了0.283 t,加上拓扑优化和隔板再设计减轻的质量,道岔梁的质量共下降了0.867 t,总下降比例为18.4%,优化效果显著。

3 结论

(1) 通过对道岔梁进行静强度分析,得到了道岔梁的受力和变形情况,承载力完全符合要求。

(2) 通过拓扑优化和进一步的尺寸优化,得出了最佳的优化方案。共删除了24块横向构件、2块纵向构件,并对横隔板进行了重新设计,共减少焊缝33条(长约30 m),有效减少了焊接工作量。结构质量共减轻了0.867 t,下降比例达18.4%,优化效果显著。

图7 尺寸优化前后应力云图

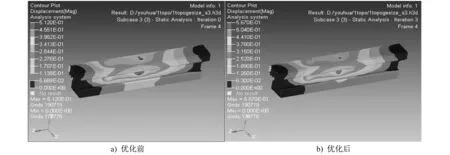
图8 尺寸优化前后位移云图

类别最大应力值/MPa最大位移值/mm质量/t优化前69.380.5124.113优化后70.000.5673.830

(3) 为进一步减轻质量,可考虑改变梁体内部的结构形式,由原来的板架结构改为桁架结构。桁架结构可充分利用材料的强度,在跨度较大的情况下比实腹梁更能节约材料,且可以增加刚度、减轻自重。

(4) 本文只考虑了道岔梁的强度、刚度及稳定性，未考虑疲劳强度。由于条件限制,只通过有限元软件进行了仿真分析,在今后的研究工作中,可以通过试验来验证结构的疲劳性和可靠性。

[1] 中华人民共和国建设部，中华人民共和国国家质量监督检验检疫总局.钢结构设计规范：GB 50017—2003[S].北京：中国计划出版社，2003.

[2] 王能.工程轨道车转向架结构优化研究[D].大连:大连交通大学交通运输工程学院,2012.

[3] 洪清泉,赵康,张攀.Opti Struct & Hyper Study理论基础与工程应用[M].北京:机械工业出版社,2012,12.

[4] 荣见华,姜节胜,颜东煌.多约束的桥梁结构拓扑优化[J].工程力学,2002,19(4):160.

[5] 王智祥,谭珊.应用ANSYS的轻轨道岔梁有限元分析[J].重庆理工大学学报,2013,27(7):37.

[6] 中华人民共和国住房和城乡建设部.跨坐式单轨交通设计规范:GB 50458—2008[S].北京：中国建筑工业出版社，2008.

Optimization of Monorail Turnout Beam Structure Based on HyperWorks

TAN Shan, WANG Zhixiang

Taking the monorail turnout beam made by the Eastern Chongqing Shipbuilding Industry as an example, the static strength of the beam turnout structure is analyzed by using finit element software HyperWorks. The results show that the beam intensity could fully meet the requirements of bearing capacity, but there is relatively large waste of materials. So the OptiStruct module in HyperWorks is used to make topology optimization and size optimization in the premise that the bearing capacity and the necessary safety margin of the beam are ensured. After the optimization, the beam weight is decreased by 18.4% with very obvious effect.

monorail; turnout beam; mathematical model; topology optimization; size optimization

U 232.2

10.16037/j.1007-869x.2016.04.014

2014-04-15)