一种新的四进制差分空间调制方法

高 强,范丽敏,韩东升

(华北电力大学电子与通信工程系,河北保定 071003)

一种新的四进制差分空间调制方法

高 强,范丽敏,韩东升

(华北电力大学电子与通信工程系,河北保定 071003)

在SM(空间调制)系统中,基于差分编码思想对4根发射天线情况提出了一种新的DSM(差分空间调制)方案。在接收端解调时采用差分直接检测法,即根据前后相邻两时刻的接收信号差进行解调。该方法只需测定初始的信道参数,后续接收端与发送端均不需要知道信道状态信息,通信过程中可以抵抗信道参数变化。对DSM方案进行了性能仿真,结果表明,该四进制DSM方案能够实现通信,并且具有较好的抗信道参数变化性能。

空间调制;差分编码;多输入多输出;差分检测

0 引 言

SM(空间调制)[1]技术最早由Raed Mesleh等人提出,其有效地提高了系统的频谱效率和传输性能[2],是一种极具潜力的新型多天线技术[3],也是5G移动通信系统无线传输关键技术的有力竞争者。SM大多假设接收端已知信道状态信息,在信道状态改变慢于符号传输速率时较为合理,但不适合高速移动场景。信道改变迅速时接收端若要获得精确的信道状态信息非常困难,其成本也会大大增加。DSM(差分空间调制)可在信道状态信息未知的情况下完成调制解调,适合高速移动场景。差分的概念在MIMO(多输入多输出)中已成功实现[4-8],也有学者提出将差分应用于SM[9-10],文献中具体阐述了发送端为两根或3根天线时,在PSK(相移键控)调制方式下DSM的编码传输。

本文针对发送端有4根天线的情况提出了一种新的DSM方案,在发送端结合差分编码的思想激活天线,接收端采用差分直接检测的解调方法。通过理论推导并进行了仿真研究,给出了抗噪声性能曲线。

1 差分空间调制

在SM系统中,假设发射天线有Nt根,接收天线Nr根。本文提出的DSM中,取Nt=4,Nr为任意值。在传统SM中,发送时隙只激活一根天线,定义S为每个时刻传输的Nt维列向量信号,且S中只有一个非零元素Si,i∈[1∶Nt]表示被激活的天线序号。H为Nr×Nt信道传输矩阵,n为Nr维列向量加性高斯白噪声,y为接收端在空间域上接收到的信号向量。对信道建模时有传统的时间域卷积关系和表达传输衰减量的乘积关系两种形式,在SM中,均采用乘积关系模型。根据文献[2]、[9]和[10],接收端的接收信号向量y可表示为

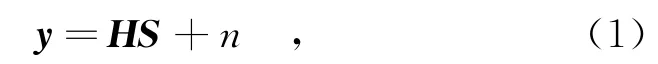
H可表示为

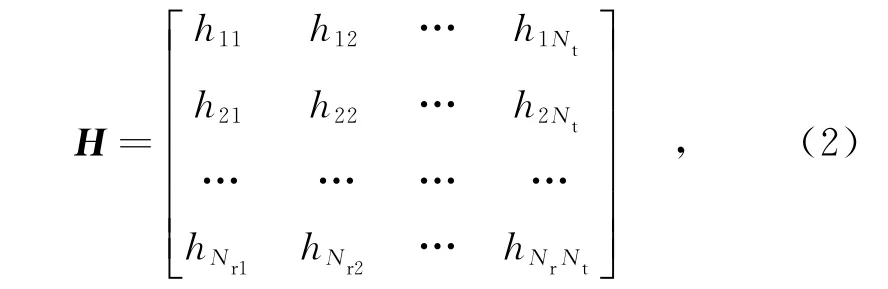
式中,hNrNt表示发射天线Nt到接收天线Nr之间的

传输信道增益,写成向量形式为

式中,hj表示从发射天线j(j∈[1∶Nt])到所有接收天线的信道增益,即

1.1 DSM编码规则

4根发射天线的DSM系统中,将4根天线两两分组,每个时刻同为一组的天线中只有一根被激活,在同一时刻被激活的两根发射天线同时工作。图1所示为差分天线的编码方式,其中,A号和B号发射天线为一组,a号和b号发射天线为另外一组。因此,同一时刻工作的天线组合为(A a)、(A b)、(B a)和(B b),分别对应图1中T4～T14种状态。天线组合方式确定后规定:当输入四进制码元为00时,当前时刻激活天线组合不变,即保持与上一时刻工作天线组合状态相同;当输入四进制码元为01时,若上一时刻激活的天线组合为T1状态,则当前时刻激活天线组合为T2状态,或者是其逆过程;若上一时刻激活的天线组合为T2状态,则当前时刻激活天线组合为T1状态,T3状态和T4状态之间跳变;当输入四进制码元为10时,激活的天线组合在T1和T3状态之间跳变、或者T2和T4状态之间跳变;当输入四进制码元为11时,激活的天线组合在T1和T4状态、T2和T3状态之间跳变。

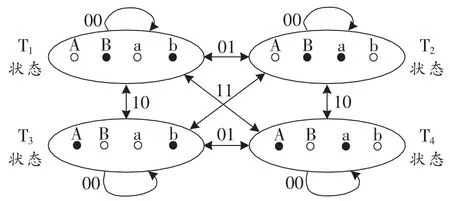
图1 天线编码方式

图1 中还具体给出了发射天线的工作状态转移图及输入不同的四进制码元时激活天线组合的跳变情况,空心圆点表示发射天线不工作,实心圆点表示该发射天线被激活。DSM即用前后相邻时刻天线组合的不同跳变来表示码元序列00、01、10或11。

1.2 DSM检测

差分直接检测法是根据DSM的特点提出的一种解调方法,其原理是根据前后两个时刻接收端收到的信号差来判断天线工作状态的跳变情况,然后恢复出激活天线组的四进制码元序列。差分直接检测与其他检测方法的最大不同是仅需要在传输开始时刻给出信道状态信息,之后可以在信道状态信息未知的情况下完成解调,这也是差分直接检测法最大的优点。

假设信道中没有噪声干扰,接收端k时刻收到的信号向量为y(k),k+1时刻收到的信号向量为y(k+1),发送端k时刻发出的信号向量为s(k),k+ 1时刻发出的信号向量为s(k+1),信道传输矩阵为H,则由式(1)可知

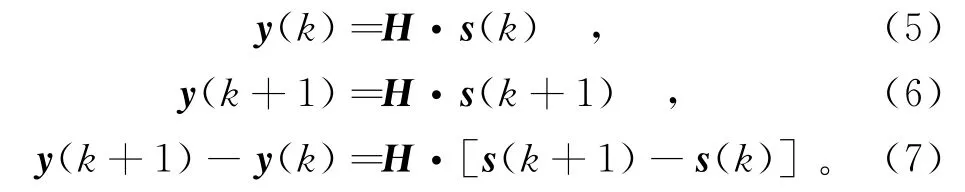
由式(7)可知,如果接收端的信道矩阵前后时刻不发生变化,则当前时刻与前一时刻收到的信号向量的差的模值只与发送信息的改变有关,即由发送信号向量决定接收信号向量,其模值大小反映了不同的状态跳变,因此能准确解调SM信息。在信道慢衰落条件下,信道矩阵变化较小,可以忽略信道参数的微小波动,认为前后时刻的信道矩阵参数近似相等,此时,仍然可以认为接收信号向量的模值变化主要是由发送信息的变化而引起,因此,也能准确解调SM信息。

若信道参数微小波动,H(k)表示k时刻的信道参数,H(k+1)表示k+1时刻的信道参数,则式(5)～式(7)可表示为

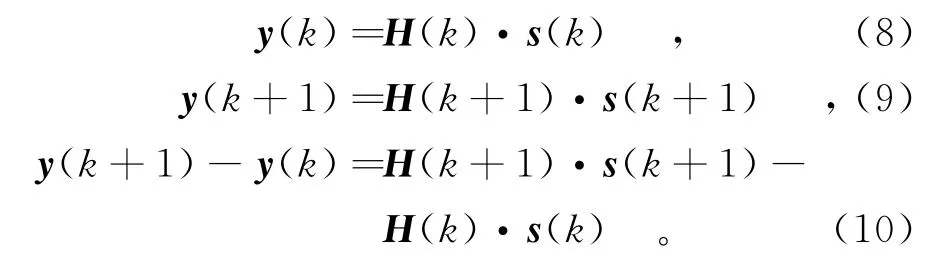
由式(3)可知,若H(k)表示为

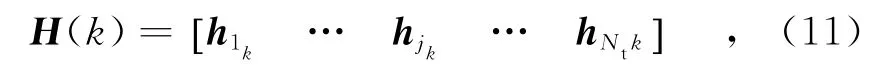
则H(k+1)可表示为

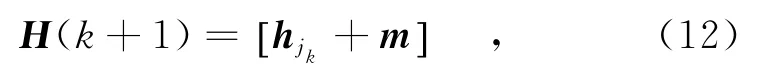
式中,j=1,2,…,Nt;m为Nr维列向量,由信道的微小变化引起。而慢衰落信道中两个相邻时刻的信道变化不会很大,几乎可以认为H(k+1)与H(k)相差不大,因此式(10)近似等于式(7)。DSM系统中,用于选择天线的四进制码元序列与前后相邻两时刻激活天线组跳变情况之间的关系如表1所示。

表1 码元与天线组跳变

由表1可知,每个四进制码元序列分别对应4种跳变情况,由于同一时刻激活两根天线,结合式(3)与式(7),可得码元与接收端的信号差如表2所示。

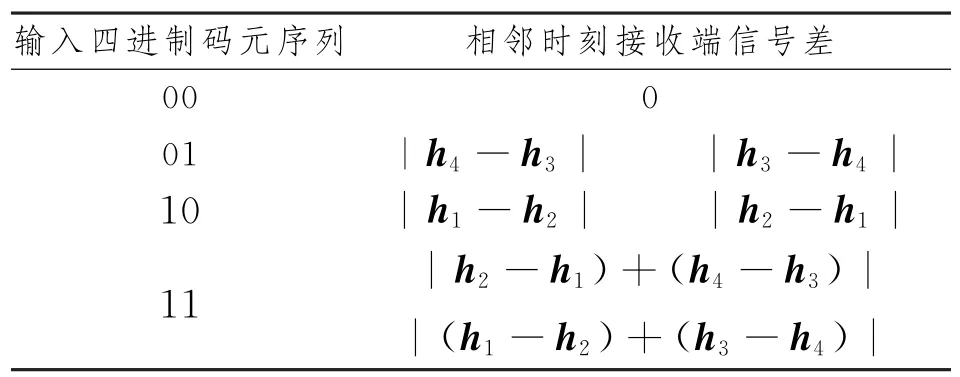
表2 码元与接收端信号差

因此,接收端解调时,在得到相邻两时刻接收信号向量差后,经过以下计算即可完成解调:

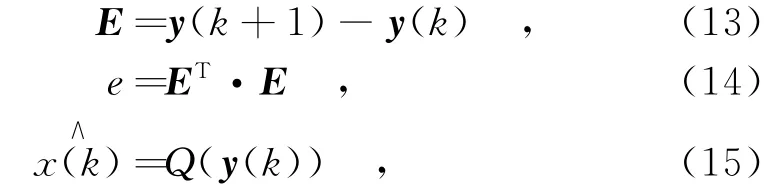
式中,E为相邻时刻接收信号向量的差向量;ET为向量E的共轭转置;e为向量E的模值;为接收端k时刻解调得到的符号。

传输开始时刻给出信道状态信息,依据信道状态信息可以分别得到表2中四进制码元序列所对应的接收端信号差。式(13)即为两个相邻时刻接收信号向量做差,得到差的列向量E,相邻时刻接收端信号差向量E经过式(14)计算后,结合表2可知,四进制码元序列01对应的两个差值是一个相同的数,同理,码元序列10对应的也是一个差值,码元序列11对应的是两个不同的差值。判断e的值并分别与表2中的差值进行比较,依据前后相邻两时刻接收信号的差值即可解调出输入的四进制码元序列。Q(·)为星座量子化函数,式(15)用于解调出调制符号,并通过SM反映射即可恢复出原始输入比特。

2 DSM系统性能分析

2.1 DSM频谱利用率

DSM系统中,发送端每个时刻发送信息的位数R(即频谱利用率)包括两个独立部分,空间域中用来选择天线跳变状态的部分和信号域里用来符号调制的部分,因此R可表示为

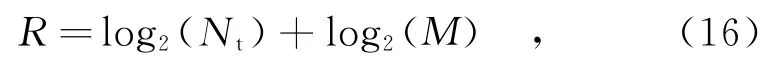
式中,M为信号调制的进制数。式(16)与文献[2]中提到的传统SM的频谱利用率相同,并未降低频谱利用率。在这方面,本文提出的天线编码方式优于文献[9]和[10],因为文献中的频谱利用率有所降低。

2.2 差分检测性能分析

差分直接检测法解调时仅仅在初始时刻需要信道状态信息,之后可在信道参数未知时完成解调,能降低信道估计的成本。由于差分直接检测法是依据前后相邻两个时刻接收信号求差进行解调,因此,在一定程度上可以对抗信道参数变化,信道参数的变化不会因为长时间积累导致变化较大进而影响解调性能。

在Nt和Nr均为4时,对SM和DSM进行仿真对比,符号调制均为BPSK(二进制相移键控)调制,信号速率为3 bit/s/Hz,由于SM是传统意义上的空间调制,发送端每个时刻只激活一根天线,因此接收端采用MRC(最大合并比)解调;DSM发送端每个时刻同时激活两根天线,接收端采用差分直接检测解调。图2所示为SM与DSM在不同信噪比时误码率的对比。

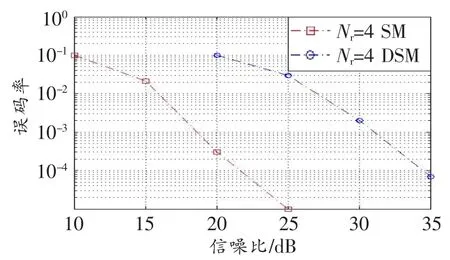
图2 两种方案的误码率对比

由图2可知,DSM的差分直接检测法比SM的MRC解调性能稍差,SM在大约22 d B时误码率为10―4,而DSM达到相同误码率需要34 dB的信噪比,但DSM仅需要知道初始时刻的信道传输矩阵,对噪声干扰的要求更高,使得接收端在没有信道状态信息时也可以完成解调,为信道质量较高的场合提供了一种新的方法。

图3所示为信道变化时的解调对比,实验环境同图2,令初始时刻SM与DSM误码率相同且均为10―4,即SM的信噪比为22 dB,DSM的信噪比为34 dB,测量该误码率下两种解调方法在信道变化随时间积累时对误码率的影响。

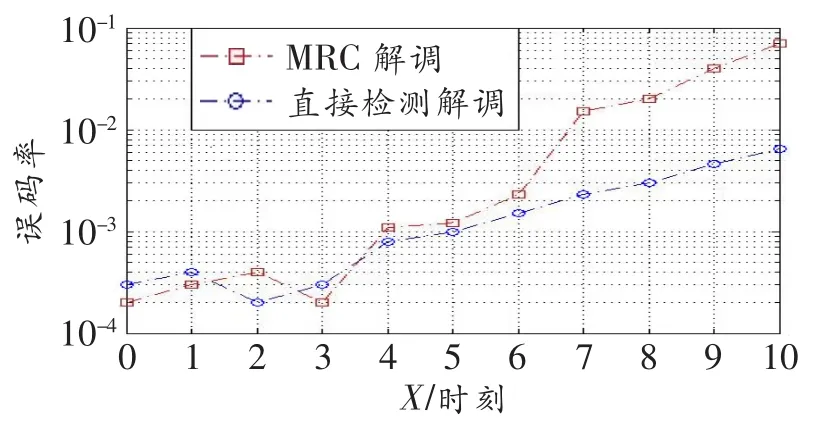
图3 信道变化时解调对比

由图3中可以看出,前3个时刻信道变化较小,

且时间积累不多,对误码率几乎没有影响。从第4个时刻开始,信道变化积累了一定时间,与初始时刻相比,信道变化较大,两种解调方法的误码率均开始上升,解调性能变差。随着第7个时刻的开始,MRC解调性能急剧下滑,差分直接检测性能虽然也变差,但仍优于MRC解调,这是因为随着信道变化积累越来越大,MRC已无法正确解调,实际中往往需要监测信道参数,并通过时时更新来解决信道变化问题。而差分直接检测法是利用前后相邻两个时刻信号差来解调,信道变化在前后相邻两个时刻不会变化太大,这种微小变化不足以引起解调性能骤变,且前后时刻做差时,信道变化也会被抵消一部分,因此在信道变化随时间延续而积累时,差分直接检测法受影响较小,性能优于MRC解调。

2.3 解调复杂度分析

以发送端和接收端天线数目均为4为例,两种算法的解调复杂度对比如表3所示。

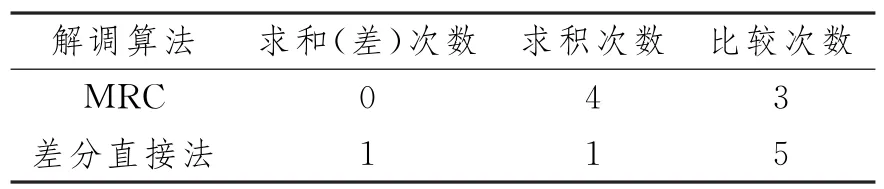
表3 解调算法复杂度对比

由表3可以看出,差分直接检测法虽然在比较次数和求和(差)次数上多于MRC解调,但求积运算次数远小于MRC,差分直接检测法并没有增大接收端解调的计算复杂度。

2.4 系统适用场景分析

结合对DSM的性能分析可知,该方案适用于信道更新频繁但信噪比高的场景,因为接收端不需要时时监测更新信道状态信息,降低了接收机的复杂度和系统成本开销。在信道质量高即噪声干扰小、信号条件较好的场景中,DSM的优势更加明显。在近距离基站与基站间传输时,该方案也是不错的选择。DSM还可应用在发送端需要自动选择天线的场景中,也为将来5G移动通信提供了一种选择。

3 结束语

本文提出了一种新的4根发射天线的DSM方案,描述了DSM传输和检测的具体实施原理。仿真研究了DSM方案的性能,给出了仿真曲线,结果表明,本文所提方案只需初始时刻的信道状态信息,之后可在信道状态参数未知的情况下完成解调,能对抗较小的慢衰落信道变化。

[1]Mesleh R,Haas H,Ahn C W,et al.Spatial modulation-OFDM[EB/OL].(2006-01-01)[2016-06-30].https://www.researchgate.net/publication/260319340_ Spatial_Modulation_-_OFDM.

[2]Mesleh R,Haas H,Ahn C W,et al.Spatial Modulation-A New Low Complexity Spectral Efficiency Enhancing Technique[C]//First International Conference on Communications and Network 2006.Shanghai,China:IEEE,2006:1―5.

[3]Jeganathan J,Ghrayeb A,Szczecinski L.Spatial modulation:optimal detection and performance analysis [J].IEEE Communications Letters,2008,12(8): 545―547.

[4]Renzo D M,Haas H,Grant P M.Spatial modulation for multiple-antenna wireless systems:a survey[J]. IEEE Communications Magazine,2011,49(12): 182―191.

[5]Tarokh V,Jafarkhani H.A differential detection scheme for transmit diversity[J].IEEE Journal on Selected Areas in Communications,2000,18(7): 1169―1174.

[6]Yu B,Yang L,Chong C.Optimized Differential GFSK Demodulator[J].IEEE Transactions on Communications,2011,59(6):1497―1501.

[7]Cho W,Yang L.Optimum Resource Allocation for Relay Networks with Differential Modulation[J]. IEEE Transactions on Communications,2008,56(4): 531―534.

[8]Huo Q,Song L,Li Y,et al.A Distributed Differential Space-Time Coding Scheme With Analog Network Coding in Two-Way Relay Networks[J].IEEE Transactions on Signal Processing,2012,60(9): 4998―5004.

[9]Bian Y,Wen M,Cheng X,et al.A differential scheme for spatial modulation[C]//GLOBECOM 2013.Piscataway,USA:IEEE,2013:3925―3930.

[10]Bian Y,Cheng X,Wen M,et al.Differential Spatial Modulation[J].IEEE Transactions on Vehicular Technology,2015,64(7):3262―3268.

A New Method of Quaternary Differential Spatial Modulation

GAO Qiang,FAN Li-min,HAN Dong-sheng
(Department of Electronic and Communication Engineering,North China Electric Power University,Baoding 071003,China)

In the spatial modulation system,a new differential spatial modulation scheme is proposed for four transmitting antennas based on differential coding.The scheme adopts the differential detection in the receiver.The differential detection is according to the difference of received signal in adjacent time,and only the initial channel parameters are required.The channel state information is not required at the transmitter and receiver sides.The change of channel parameters can be ignored in the process of communication.The simulation results show that the quaternary differential spatial modulation can not only realize communication,but also has good ability to resist the change of channel parameters.

spatial modulation;differential coding;multiple-input-multiple-output;differential detection

TN929.5

A

1005-8788(2016)06-0059-04

10.13756/j.gtxyj.2016.06.017

2016-06-30

国家自然科学基金资助项目(61302106);河北省自然科学基金资助项目(F2014502029)

高强(1960―),男,河北涿州人。教授,博士,主要研究方向为通信和信号处理。

范丽敏,硕士研究生。E-mail:1345731131@qq.com