一种短时信号精测频方法

吴 扬, 柴 恒

(中国船舶重工集团公司第723研究所，扬州 225001)



一种短时信号精测频方法

吴 扬, 柴 恒

(中国船舶重工集团公司第723研究所，扬州 225001)

脉冲信号的时宽限制了采样点的个数, 使得短时信号的频率测量精度无法提高。提出了一种短时信号精测频方法，该方法能显著提高测频精度，从而给雷达信号的分选、识别及特定发射机识别(SEI)提供了很好的稳定度。

频率测量;窗函数;短时信号;幅频特性

0 引 言

在数字信号处理中，信号经过模/数变换后由模拟信号变换为数字信号，在采样率固定的情况下，信号的持续时间越短，数字信号的采样点数就越少，根据快速傅里叶变换(FFT)定理，假设采样率为fs，信号采样点数为N，那么信号的测频精度与采样点数N成正比，也就是采样点数越多测频精度越高。但是脉冲信号的时宽限制了采样点的个数，所以必须采用改进的方法对频率进行测量，以提高短时信号的频率测量精度。

1 傅里叶变换和窗函数

傅里叶变换作为数学工具被经常使用在信号处理中，它将信号从时域变换到频域，可用以研究时域和频域间的关系。但在工程实际中并不是取无限长信号进行测算，因为一些条件的限制，只能取有限的时段进行分析，利用周期延拓处理，将所取信号在时间域上从有限时间转换成虚拟无限长，然后再对其开展傅里叶变换等数学处理。这种信号截取函数称为窗函数。

根据采样定理，采样频率无论取值多少，信号一旦被截断就会引起混叠，产生误差；另外原始信号被截断后，其频域的能量与分布会被扩展，其频谱必然会发生畸变，这种畸变现象被称为频谱泄漏。 该泄露为傅里叶变换所固有，无法避免，只能设法控制在一定范围以内。

频谱泄漏程度与窗函数的形状密切相关，会受到窗函数的主瓣和旁瓣高度差、主瓣宽度、旁瓣衰减速度这3个形状参数的影响。当这3个参数的值让所截取的信号能量主要集中在主瓣时，频谱泄漏程度就会比较低，这时频谱分析结果就会比较真实。因此不同类型的信号可以通过选择合适的截取函数(即窗函数) 来减少频谱泄漏。

窗函数主要分以下几种类型：

(1) 指数窗函数：这类窗函数采用了指数时间函数，比如高斯窗函数，当被测信号函数随时间按指数衰减时适合用此类窗函数。

(2) 幂窗函数：该类窗函数使用时间变量某种幂次的函数，例如三角形、矩形或者其它时间x(t)的高次幂，当被测信号的主瓣频率要求准确且其它精度要求不高时可用此类窗函数。

(3) 三角函数窗函数：该类窗函数采用正弦、余弦函数等三角函数组合成的复合函数，比如海明窗、汉宁窗，当被测信号为随机或未知时适合用此类窗函数[1]。

2 短时信号精测频方法

该方法首先对信号进行加窗处理，然后对加窗滞后的信号进行FFT变换，求出其幅度响应；其次，根据其幅度响应进行频率粗测量，进而确定频率测量时积分的上下限；最后根据积分的上下限对信号的频率进行精测量。本方法通过进行2次测量，能显著提高测频精度，如时宽1 μs的点频信号的测量精度能够达到误差绝对值小于10 kHz。

2.1 短时信号精测频流程

该种短时信号精确测频方法首先采用粗测频来确定精测频的积分范围，只用一次FFT运算就能显著提高短时信号的测频精度。短时信号精测频方法流程图如图1所示。

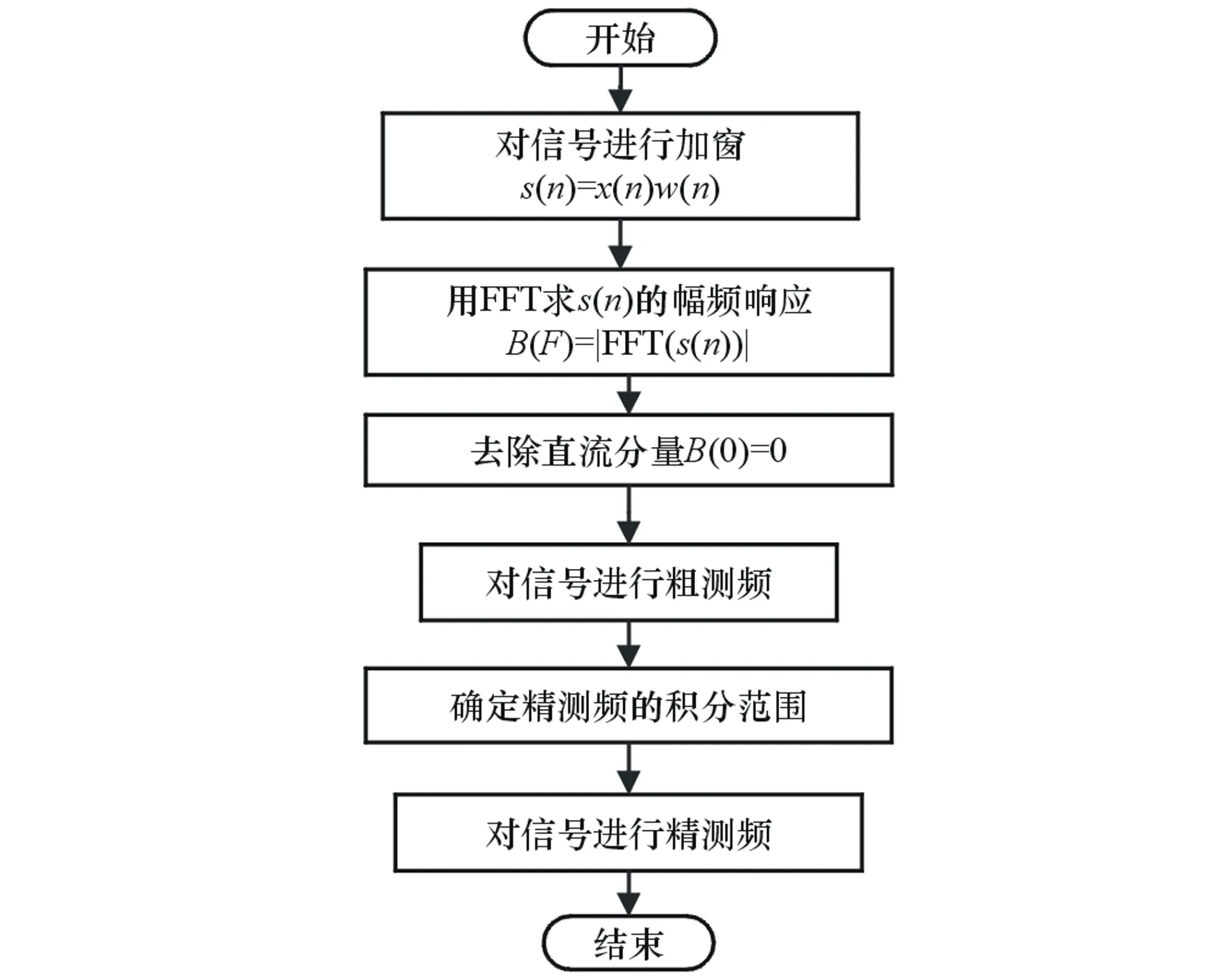
图1 短时信号精测频的方法流程图

2.2 短时信号精测频详细步骤

计算方法和窗函数的选取及积分上下限的选取按如下步骤进行：

(1) 根据信号长度计算窗的长度

在采样率fs固定、信号时宽τ固定的情况下，信号的长度符合以下公式：

N=τfs

(1)

通常情况下，信号时宽τ也是估计出来的，具体的估计方法在这里不再进行叙述。

(2) 计算窗函数

窗函数的类型有很多种，常用的窗函数有高斯窗、海明窗、汉宁窗、Blackman窗等窗函数，本文采用高斯窗进行加窗处理。高斯窗函数的模型如下式所示[2]：

(2)

高斯窗函数信号如图2所示。

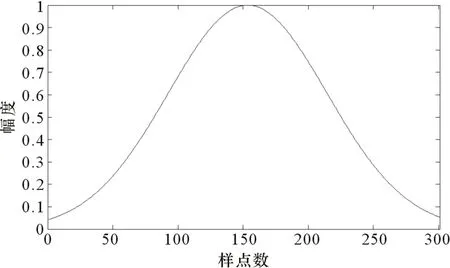
图2 高斯窗函数信号

(3) 对原始信号进行加窗处理

窗函数的长度与原始信号的长度相等，加窗处理即用原始信号与窗函数相乘：

s(n)=x(n)w(n)

(3)

图3和图4分别为加窗处理前的原始信号和加窗处理后的信号。

图3 原始信号

(4) 对加窗处理后的信号进行FFT运算[3]

获得信号频域内的特征：

(4)

(5) 求信号的幅频特性

对信号进行粗测频：

(5)

图5为信号的幅频特性图。

图5 信号幅频特性

(6) 去除幅频特性的直流分量

将直流分量B(0)直接置零，以去除其对测频的影响：

B(0)=0

(6)

根据信号频域幅度响应求信号的平均频率，采

用如下公式：

(7)

(8) 确定精测频的积分范围

(9) 对信号进行精测频[4]，求得信号的精确频率fr：

(8)

3 结束语

对于短时信号，在采样频率固定的情况下，频率的精确测量受制于信号的时宽，采用精确频率测量方法，在增加很小运算量的情况下，大大提高了短时信号的频率测量精度，在中频100 MHz、脉宽1 μs、采样率为1 GHz的情况下，测频精度的绝对误差小于10 kHz，这对于雷达信号的分选、识别及个体识别提供了很好的稳定度。

[1] 刘波,彭骁寒.数字信号处理中加窗优化处理的研究[J].计算机与数字工程,2014,42(3):471-474.

[2] 薛年喜.MATLAB在数字信号处理中的应用[M].北京:清华大学出版社,2008.

[3] 侯民胜,邹平,朱莹.FFT在现代雷达中的应用[J].电子测量技术，2009,32(4):9-11.

[4] 陈卫东,杨绍全.加窗离散傅里叶变换测频分辨率研究[J].西安电子科技大学学报，2000,27(2):157-160.

An Accurate Frequency Measurement Method for Short-time Signal

WU Yang,CHAI Heng

(The 723 Institute of CSIC,Yangzhou 225001,China)

The time width of pulse signal limits the number of sampling points,which makes the frequency measurement accuracy of short-time signal unable to be improved.This paper presents a kind of accurate frequency measurement method for short-time signal,this method can obviously improves the frequency measurement accuracy,accordingly provides good stability for the radar signal sorting,identification and specific emitter identification (SEI).

frequency measurement;window function;short-time signal;amplitude-frequency characteristic

2016-03-16

TN971.1

A

CN32-1413(2016)03-0071-03

10.16426/j.cnki.jcdzdk.2016.03.018