一种PRI变化的雷达信号无源定位方法

陈晓威，李彦志，张国毅

(空军航空大学，长春 130022)



一种PRI变化的雷达信号无源定位方法

陈晓威，李彦志，张国毅

(空军航空大学，长春 130022)

目前脉冲重复间隔(PRI)恒定的雷达信号已经越来越少，取而代之的是PRI变化的雷达信号。传统的相位差变化率定位法均假设PRI恒定，没有考虑因PRI变化引起的相位差变化率测量误差和定位误差。提出了一种利用插值法重新构造相位差数据的方法，提取了相位差变化率并进行了定位解算。仿真结果表明采用该相位差数据重构方法能够实现快速高精度的无源定位。

无源定位；插值；相位差重构；相位差变化率

0 引 言

相位差变化率定位技术是一种很有应用前景的快速高精度无源定位技术，是战术电子侦察中不可或缺的一个重要环节，对于获取敌方雷达部署情况、战场态势，确保雷达情报的完整性具有无法替代的作用。

传统的相位差变化率定位法大都假设以固定的观测间隔侦收信号。而目前脉冲重复间隔(PRI)恒定的雷达信号已经越来越少。当辐射源信号的PRI变化时，信号的观测间隔也随之变化，会导致传统的提取相位差变化率的方法失效。文献[1]采用最小二乘线性拟合提取PRI变化信号的相位差变化率，并用于相位差变化率定位法计算中。但是相位差是关于方位角的正弦函数，是非线性变化的，采用最小二乘线性拟合构造的相位差数据是线性变化的，破坏了其非线性特性，相当于人为地引入了固定偏差，使得拟合得到的斜率(相位差变化率)是恒定值。在相位差测量误差较大(σ>10°)时，拟合得到的恒定相位差变化率数值相对于其真实值可能出现发散的情况，导致了对相位差变化率的估计精度不稳定。因此这种针对PRI变化雷达信号辐射源的相位差变化率定位法鲁棒性差。本文提出利用插值法对非等观测间隔的相位差测量数据进行重构，获得等观测间隔的测量数据，再利用Kalman滤波法估计出相位差变化率进行定位解算。本算法计算量小，简单可行，能够满足快速高精度无源定位的要求。

1 建立二维相位差变化率定位模型

文中假设相位差数据已经过解模糊处理，所以利用一维单基线相位干涉仪模型测量目标辐射源到达干涉仪的相位差及其变化率参数，通过定位算法求解观测器与目标之间的径向距离，实现即时定位。一维单基线干涉仪的原理如图1所示[2]。

图1 干涉仪基线方向与信号入射角关系示意图

图1中，α表示以干涉仪基线的法线方向为基准测得的信号入射角。

以地面某一固定点作为坐标原点O，建立二维平面直角坐标系OXYZ，如图2所示[3]。

图2 载机与目标辐射源相对位置图

设OX轴的正向为正东方向，OY轴的正向为正北方向。在OXYZ坐标系下的地面未知辐射源所处位置为P(xT,yT)，机载观测器的坐标为A(x,y)，并以某一航向角以速度V作匀速等高直线飞行，与目标辐射源之间存在相对非径向运动，并且不考虑机身抖动引起的误差。观测器与未知辐射源之间的径向距离为R。设OX轴正向为参考方向，β代表载机运动方向与参考方向间的夹角，即航向角。θ代表载机与未知辐射源间的径向方向与参考方向的夹角，即辐射源的方位角。由文献[3]可得测距公式为：

(1)

式中：fT为辐射源的信号载频；α为信号的入射角；d为干涉仪基线长度；φ′为相位差变化率；c为光速。

推导出目标辐射源的位置公式为：

(2)

2 相位差及其变化率的变化规律

假设来波信号的PRI为0.001 s，理想情况下，来波信号的观测间隔等于信号的PRI，故观测间隔T=0.001 s。信号的载频fT=3 GHz，测频误差服从高斯白噪声分布且σfT=3 MHz，航向角β=0°，观测器的运动速度V=(300,0) m/s，瞬时速度扰动噪声σV=0.1 m/s，固定目标的位置为(107.15,399.88) km，观测器的运动起点为(0,0)km，观测器自身定位误差均方差为σp=10 m，相位差测量误差为高斯白噪声，设解模糊后相位差测量均方误差取σφ=0.261 8 rad，仿真时间5 s。短时间内的相位差数据仿真如图3所示。

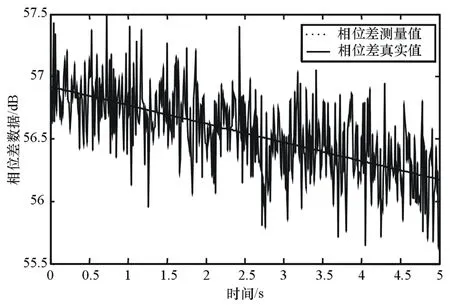
图3 相位差数据变化规律

实际侦察中，载机在较短的时间内保持匀速直线等高飞行是可能的，并且相位差真实值随时间呈近似线性变化。因此，在相位差变化率测量精度要求不高的前提下，可以近似将其认为是一个恒定的数值[4]。

3 基于插值的PRI变化信号定位法

3.1 基于分段插值的相位差重构

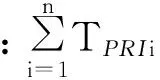
i=1,…,n,N∈Z+

(3)

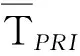
3.2 典型的插值方法

典型的一元插值法包括Lagrange插值、Newton插值、分段线性插值、三次样条插值、Hermite插值[5]。其中采用Hermite插值法时由于需要知道被插值函数的一阶导数，而相位差的一阶导数即相位差变化率，为需要求出的测量值，因此Hermite插值法不适用于本文建立的模型。本文选取Lagrange插值、Newton插值、分段线性插值、三次样条插值，比较这4种插值函数处理PRI变化信号相位差数据的能力。

3.3 算法流程描述

对PRI变化情况下的相位差数据处理以及定位解算的流程如下：

(1) 用小波降噪算法对解模糊后的相位差测量数据进行去噪处理，便于后续插值处理；

(2) 对1组PRI数值求和，除以选取的正整数N，从而得到新的PRI值，并构造出1组新的等间隔的脉冲到达时间；

(3) 利用插值法求出等间隔时刻对应的相位差数据；

(4) 将重新构造的相位差数据用Kalman滤波法提取相位差变化率，并进行定位解算。

4 仿真结果和分析

4.1 提取相位差变化率的仿真分析

假设相位差的测量误差σφ为0.174 5 rad，以PRI参差信号、PRI正弦调制信号为例，利用基于分段插值的相位差数据重构法估计出这2种信号的相位差变化率，插值函数选取为Lagrange插值、分段线性插值、三次样条插值、Newton插值，仿真条件同3.1节所述，并且对每个插值函数作1 000次Monte Carlo循环，取相位差变化率测量值的平均值作为仿真结果，仿真时间20 s。

仿真一：PRI参差信号。

设PRI参差信号为三级参差，T=0.01 s，ΔT=0.003 s，其3个PRI分别为T-ΔT、T、T+ΔT，仿真结果如图4所示。

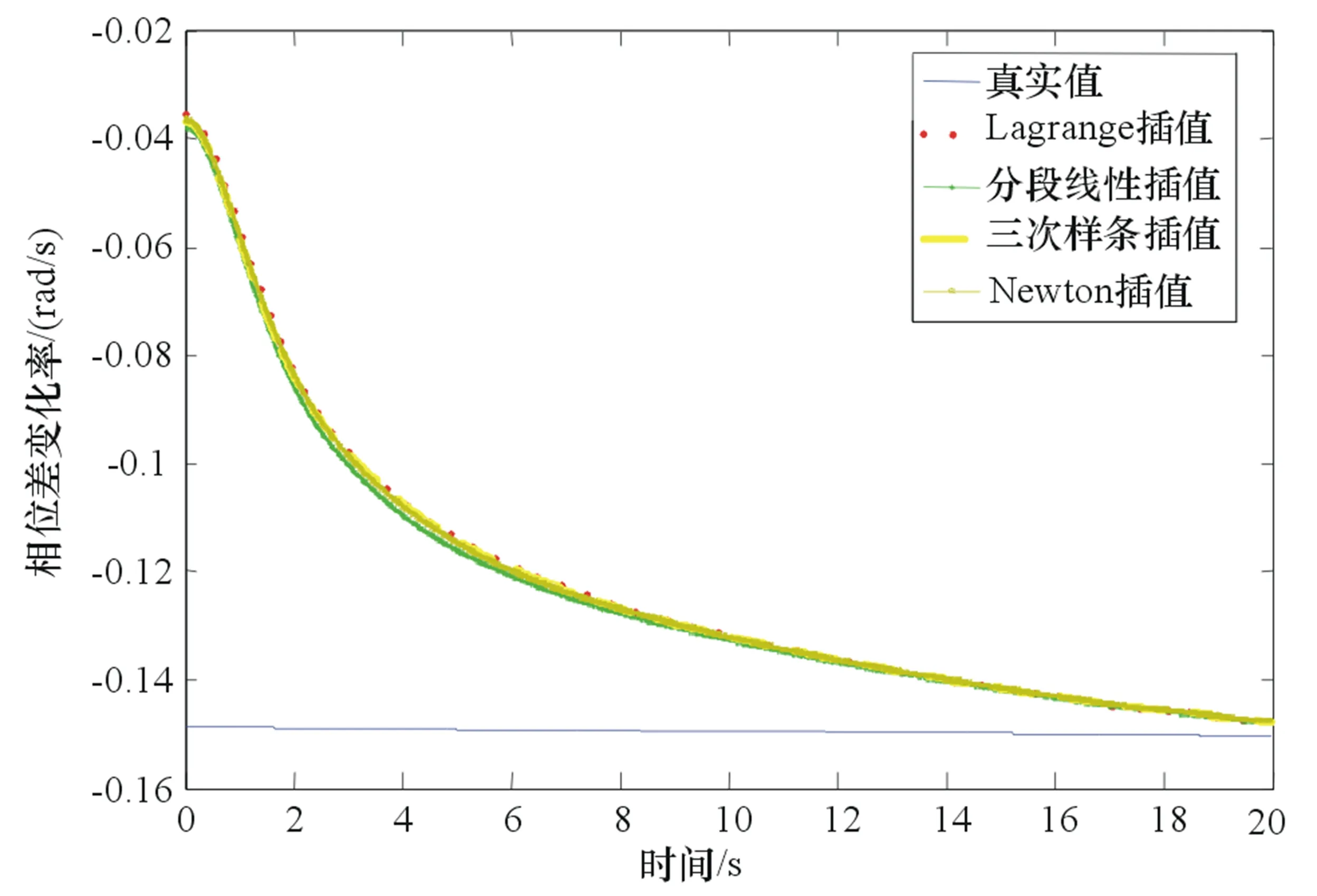
图4 PRI参差信号的相位差变化率测量结果

仿真二：PRI正弦调制信号，其PRI均值为0.01 s，调制幅度为0.3，仿真结果如图5所示。

图5 PRI正弦调制信号的相位差变化率估计结果

从图4～图5的仿真结果可以看出，对于PRI参差信号、PRI正弦调制信号，相位差变化率的测量值经过一段时间的脉冲积累后，均能逐步逼近真实值，并且这4种插值函数都能够满足相位差数据的特点，可以认为时间越长，相位差变化率的测量精度越高。对其他PRI调制样式信号的大量仿真实验发现也能得到上述结论，说明了基于分段插值的相位差重构在理论上是可以用于处理PRI变化信号的。

4.2 定位结果的仿真分析

从4.1节的仿真分析可知：基于分段插值的相位差变化率估计法比最小二乘线性拟合法在测量精度上更具有稳定性。因此，下面分别在PRI参差信号、PRI正弦调制信号的条件下，对该提取方法在定位应用中的有效性进行仿真分析和验证，相位差测量误差分别取0.174 5 rad、0.261 8 rad，对应的仿真时间分别为20 s、25 s，其余参数设置和仿真条件同前所述。1 000次Monte Carlo运算结果如图6～9所示。

图6 σφ=0.174 5 rad、仿真时间为20 s的相对定位误差

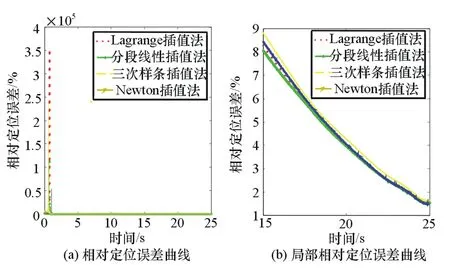
图7 σφ=0.261 8 rad、仿真时间为20 s的相对定位误差

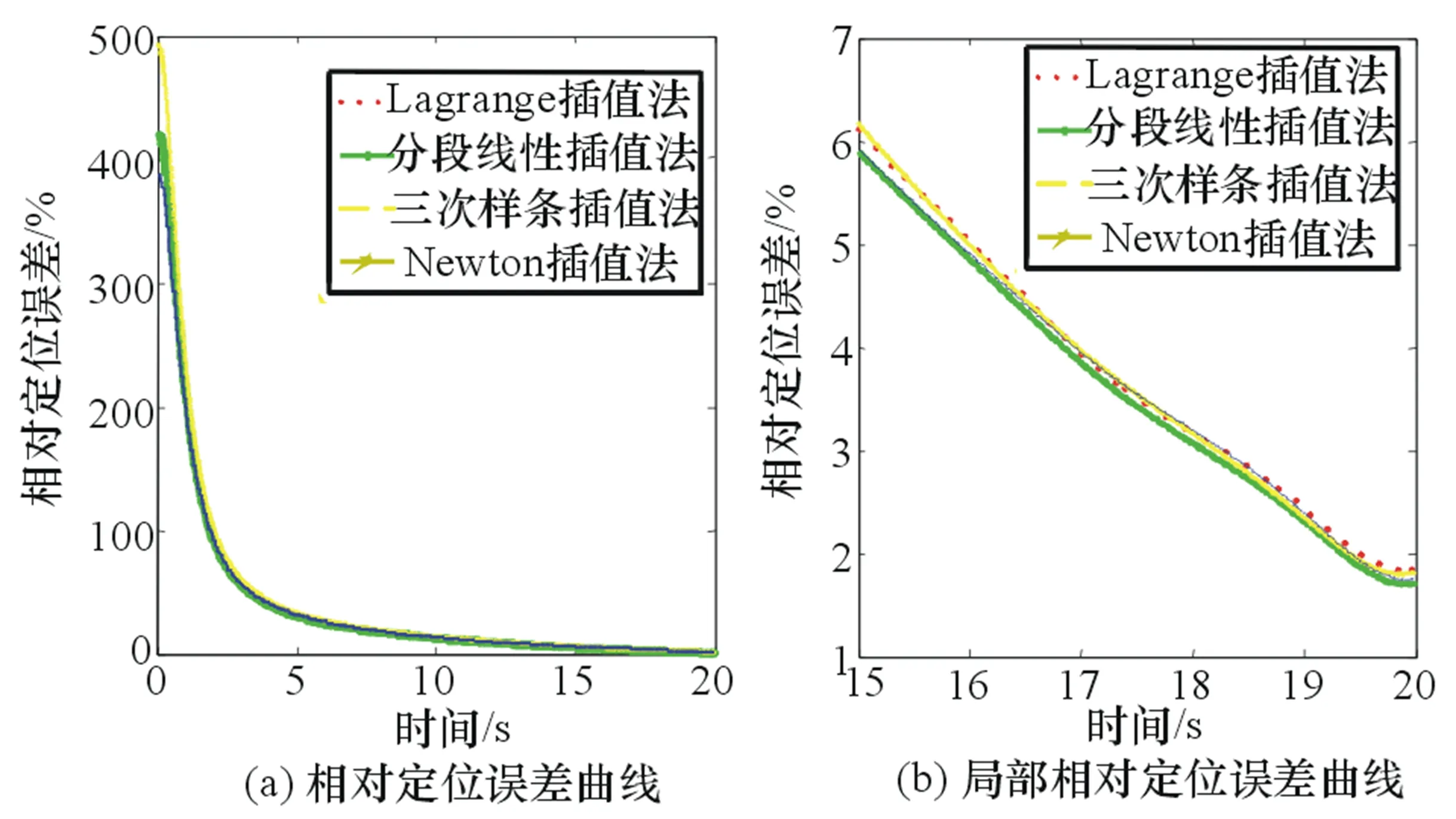
图8 σφ=0.174 5 rad、仿真时间为25 s的相对定位误差

图9 σφ=0.261 8 rad、仿真时间为25 s的相对定位误差

通过图6～图9的相对定位误差仿真结果发现，本章提出的PRI变化信号定位方法在定位收敛速度上虽然比基于最小二乘拟合的相位差变化率定位法慢，但是定位误差收敛至5%以下所需时间仍然是可以接受的。而且该定位方法鲁棒性强，没有出现定位精度发散的现象，经过一段时间的脉冲积累后能达到较高的定位精度。当σφ=0.174 5 rad时，在16 s左右能够将相对定位误差收敛至5%以下，在20 s时相对定位误差收敛至1.7%左右，达到了高精度定位。当σφ=0.261 8 rad时，定位精度收敛速度减慢。在仿真初期，定位误差相当大；但是随着脉冲的积累，定位误差迅速减小，在25 s时分别能达到1.6%和3%的相对定位误差。随着定位时间的延长，定位精度还能提高。

5 结束语

本文提出了基于分段插值的相位差数据重构方法，再利用Kalman滤波法对重构的相位差数据估计出相位差变化率测量值。最后，通过仿真验证了本文提出的相位差变化率提取方法估计精度高，适用于无源定位，且不受插值函数类型的影响。该算法简单有效，计算量小，具有较强的工程应用价值。

[1] 张国毅,宋德亮,陈枫.PRI变化雷达信号相位差变化率定位法研究[J].舰船电子对抗,2010,33(3):35- 38.

[2] 张国毅,宋德亮,王长宇.相位差变化率定位法中缺失值精确填补研究[J].吉林大学学报(信息科学版),2010,28(1):20-26.

[3] 李炳荣,曲长文,王欣欣.机载快速无源定位原理及误差分析[J].弹箭与制导学报,2005,25(4):291-293.

[4] 黄登才,丁敏.测相位差变化率无源定位技术评述[J].现代雷达,2007(8):32-34.

[5] 胡祖炽，林源渠.数值分析[M].北京：高等教育出版社，1986.

A Passive Location Method of The Radar Signal with Variational PRI

CHEN Xiao-wei,LI Yan-zhi,ZHANG Guo-yi

(Aviation University of Air Force,Changchun 130022,China)

Currently,radar signal with constant pulse repetition interval (PRI) is less and less,instead of this is radar signal with variational PRI.Traditional location method of phase difference change rate almost supposes that PRI is constant,hasn't considered the measuring error of phase difference rate and position error due to the change of PRI.This paper puts forward a kind of method to reconstruct phase difference data by means of interpolation method,abstracts the phase difference rate and performs location calculation.The simulation results show that the method to reconstruct phase difference data can quickly achieve passive location with high accuracy.

passive location;interpolation;reconstruction of phase difference;phase difference rate

2015-06-19

TN971.1

A

CN32-1413(2016)03-0011-04

10.16426/j.cnki.jcdzdk.2016.03.003