漠大线因冻胀引起的应变影响因素研究*
2020-12-28张旭顾晓婷杨燕华曹平臧雪瑞
张旭 顾晓婷 杨燕华 曹平 臧雪瑞
(长江大学石油工程学院 武汉 430100)
0 引言
冻胀是多年冻土地区地基土的常见变形。管道穿越不连续冻土区,因温度变化,土体性质发生改变,导致土体结冰体积增大,致使管道向上翘起、产生不均匀变形甚至发生弯折和泄漏。漠大线指漠河—大庆段共926 km,是我国第一条完全意义上穿越永久冻土区域的大口径长距离输油管道。其中漠河—加格达奇大杨树段,管线共计440 km,该段地理环境极其复杂,穿越包括岛状冻土的大兴安岭多年冻土区、不连续冻土和连续冻土[1]。漠大线实际运行油温全年都在0 ℃以上,属于正温输送,3 站的年平均油温在4.40~9.99 ℃,冬季和夏季记录到的最低和最高油温分别为 0.42、16.2 ℃,所以目前管道还没有发生明显的冻胀病害。但如果运行油温发生变化,管道经过多年冻土区和季节性冻土区域,加上低气温的影响,管道可能会遭受冻胀影响,对管道的安全运行造成威胁。
国外,RAJANI B等[2]率先采用有限元法对管道冻胀受力情况进行分析,介绍了一个简化的Winkler模型在模拟法国Caen管道在不同冻胀下的时变响应中的应用,并进一步证实Winkler模型也可用于分析大直径管道的差异冻胀;KIM K等[3]建立了准二维显式有限差分模型,并将偏析势(SP)概念应用于模型中,模拟分析结果与实测结果吻合较好;WEN Z等[4]针对中俄原油管线漠大线提出了一种简单的热弹塑性有限元计算模型,结果表明,管道的有效应力随冻胀变形呈线性增长;WANG Y等[5]建立了一个模拟土壤冻结过程的数值模型,并探讨土壤冻结及相关管道变形的特性对于冻土的研究。国内,吉延峻等[6]选取中俄原油管道沿途各地貌单元的典型土样进行试验,并其沿线不同地貌单元的冻胀性进行了评价;WU Y P等[7]运用模拟软件模拟分析了由冻土区差异性冻胀导致的管道应力应变变化,保证管道安全的同时,给出了土壤的最大冻胀率和相应的冻胀变形;胡宗柳等[8]对土体及管线内的温度场进行了数值模拟,研究在周期性载荷的作用下,土壤内部冻胀问题的温度分布情况;狄彦等[9]、胡渊等[10]、高东方等[11]建立了管道与土壤的相互作用和管道周围温度场模型,探讨不同管温(输运温度)工况下冷输天然气管道对管周土体冻融过程和多年冻土热稳定性的影响。
为了减少管道因冻胀地质灾害造成的损失,对管道可能发生冻胀的部位进行加强,或者采用其他减小因地质灾害给管道带来影响的措施显得尤为重要。目前我国对多年冻土区建设油气管道的工程中,仅有多年冻土工程地质勘探规范和通用的输油管道工程设计规范,在处于低温条件下及多年冻土区的油气管道工程运行、施工等安全难以保证[12]。对于埋设在冻土地带的管道缺乏合理的计算模型,在计算冻土区管道的危险截面位置时可能会导致计算结果与实际情况相差较大,威胁到管道的安全运行,造成经济损失和环境污染。因此,在研究冻胀对冻土中埋地管道的影响时,必须考虑所有影响管道应力的因素。因冻土区管道应变的设计方法的提出与运用,且管道的应变能更准确地描述出管道极限变形的状态,故研究冻土区管道因冻胀引起的应变变化十分有必要。保障管道的安全性、耐久性,需要对管道的危险截面进行合理的分析,对影响管道稳定运行的参数进行相关性分析,并对相关参数进行敏感性分析,保证管道在使用寿命周期内可以安全、有效地运行。本文用非线性数值模拟分析研究中-俄原油管线漠大线冻土区敷设的埋地管道遇到冻胀地质灾害条件下,管道的应变变化和不同参数对管道应变的影响规律,为中俄原油管道的安全运行提供理论依据。
1 管—土相互模型的建立
1.1 土体模型、管道模型参数的确立
本文需要建立的土体模型选择Drucker-Prager模型,通过查阅相关文献[13],计算模型时,管道水平方向热力影响范围与管径、埋深和介质温度成正比,对长距离大口径埋地油气管道,一般取值为30~60 m,管道垂直方向热力影响10~30 m,因此,选取40 m×10 m×60 m为土体模型尺寸。
土体竖直方向分为多年冻土层和活动土层两个部分,冻胀条件下管-土相互作用模型的土体具体参数如表1所示。

表1 土体的主要参数
本文冻土区冻胀作用下管土相互作用有限元模型,管道直径选为813 mm,壁厚设置了12.5、14.2、16 mm共3种壁厚,管道长度设置为 60 m。具体管道参数如表2。

表2 管道的主要参数
1.2 边界条件和网格设置
土体和管道边界条件如下:①对管道两端施加轴向约束;②土体的基岩底面施加完全约束[14];③与管道平行的土体两端面施加水平方向的位移约束;④与管道轴向相交的两端面,约束水平和法向的线位移以及旋转位移,不约束竖直方向的线性位移和旋转位移;⑤土体上翘可以在土体下端施加位移载荷来体现。
对管土接触区域的网格进行局部加密,以保证该区域求解结果的精度。管道和土体均采用C3D8R单元。土体网格总体划分示意见图1,管道模型网格划分见图2。

图1 土体网格总体划分示意

图2 管道模型网格划分
2 模型验证
本章采用冻胀段长度为20 m,埋深为1.8 m,壁厚为12.5 mm时的冻胀条件下的管-土相互作用有限元模型计算其应力变化,并与王勇等[15]所著文中所得到的冻胀条件下管道应力变化作对比。分别对比了管顶与管底的应力变化,见图3、图4。

(a)本章模型管顶应力
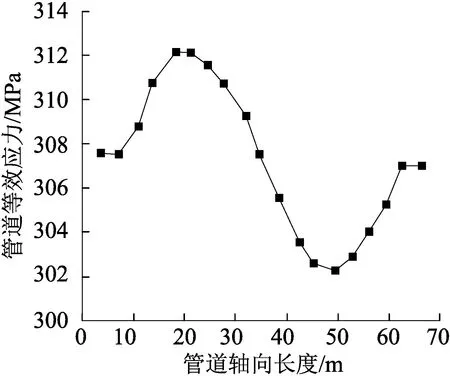
(a)对比文献模型管顶应力
从图3、图4可以看出管道顶部的应力变化均是先增大后减小再增大的趋势,而管道底部应力变化是先减小后增大再减小的趋势。本章所建模型与文献模型的管道应力变化趋势是相同的,因此本章所建管-土相互作用模型所分析的数据较为可靠。
3 管道应变的影响因素分析
通过建立管-土相互作用三维有限元模型,主要分析不同冻胀段长度、管道埋深和管道壁厚对于管道应变的影响。下面以冻胀段长度为10 m和25 m,埋深为1.8 m,壁厚为12.5 mm时的管-土模型为例。管道的最大等效应变发生在管顶和管底,在不同管道埋深和管道壁厚的情况下,因冻胀段长度不同管道的应变集中发生处也不同,见图5、图6。
图5中可以看出,管道应变集中区位于管顶和管底。通过对不同情况的模型模拟计算发现,当冻胀段长度为10 m和15 m时,管顶的应变集中现象发生在非冻胀段与过渡段的交界面,管底的应变集中现象发生在冻胀段中部区域。此时管道的最大等效应变值是位于管底的。图6该管道在管道底部有两个应变集中区域,管道总共出现了4个应变集中区域。通过对不同情况的模型进行模拟分析,管道顶部的应变集中现象发生在非冻胀段与过渡段的交界面,管道底部的应变集中现象发生在过渡段与冻胀段的交界面,而此时,管道的最大应变值位于管顶。当冻胀段长度小于20 m时,管道最大等效应变处会位于管道底部。而当冻胀段长度大于等于20 m时,管道的最大应变值位于管顶。

图5 长度为10 m时管道应变云图

图6 长度为25 m时管道应变云图
3.1 冻胀段长度对管道应变的影响
保持管道壁厚为12.5 mm不变,选取冻胀段长度为10、15、20、25、30 m共5种冻胀段长度,管道埋深分别设置为1.8、2.0、2.2 m。管道顶部的最大等效应变与冻胀段长度的关系图如图7、图8所示。

图7 最大等效应变与冻胀段长度关系(管顶)

图8 最大等效应变与冻胀段长度关系(管底)
从图7中可以看出,管顶应变最大值位于冻胀段长度为10 m处,不同管道埋深管道应变值差别小,约为0.137 7%。冻胀段长度为10~15 m时,应变减小的幅度约为1.84%;应变最大增幅约为0.22%。管道应变的减小幅度明显大于管道应变的增加幅度,在冻胀段长度为10 m时,管道受到上覆土的压力比因冻胀土体给管道的向上的径向力小,而后,冻胀段长度增加,管道受到的上覆土的压力也逐渐变大,因冻胀土壤对管道向上的径向力与管道上覆土对管道的压力逐渐相等,所以后面管顶应变会逐渐增大。
从图8中可以看出,在管道壁厚和管道埋深情况相同时,在冻胀段长度为10~20 m时,管底应变随冻胀段长度的增加而减小;在冻胀段长度为20~30 m时,管底应变冻胀段长度的增加而增大。管底应变最值分别位于冻胀段长度为10 m和20 m处,冻胀段长度为10 m时,管底应变值最大,约为1.420%;冻胀段长度为20 m时,管底应变值最小,约为0.132 1%。冻胀段长度处于10~20 m时,管底应变值减小幅度约为4.03%;冻胀段长度处于20~30 m时,增幅最大约为0.378%。管底应变减小时的应变变化幅度明显大于管底应变的增加幅度,且3种埋深的情况下,管底应变的应变值差距并不大。
图9是冻胀段长度与管道最大等效应变的关系图。总体来说管道最大等效应变是一个先减后增的趋势。冻胀段长度处于10~20 m时,管道应变随冻胀段长度的增加而减小;冻胀段长度处于20~30 m时,管道应变随冻胀段长度的增加而增大。
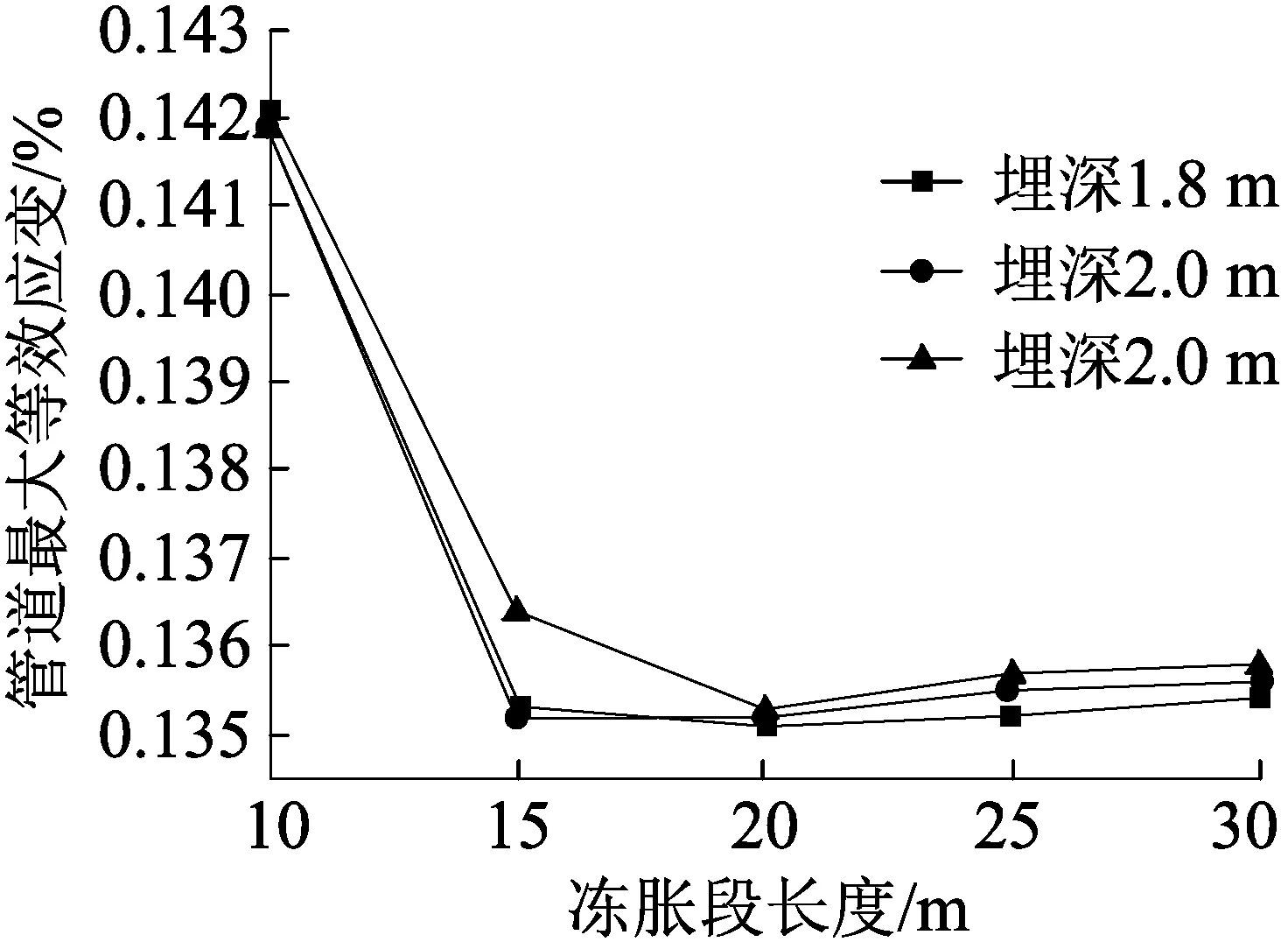
图9 管道最大等效应变与冻胀段长度关系
从图9可以看出管道应变的减小幅度明显比管道应变增加幅度大。表3是管道应变值的变化,可以看出冻胀段长度处于10~20 m时,管道最大等效应变从0.142 1%减小至0.135 3%,减小幅度为4.79%;冻胀段长度处于20~30 m时,管道最大等效应变由0.135 7%增加至0.135 8%,增加幅度为0.296%。

表3 冻胀段长度对管道应变的影响 %
3.2 管道埋深对管道最大应变的影响
保持管道壁厚为12.5 mm不变,改变冻胀段长度,分析了1.8 m、2.0 m和2.2 m 3种管道埋深情况,冻胀段长度分别设置为10 m、15 m、20 m、25 m和30 m共5种冻胀段长度。管道顶部的最大等效应变与管道埋深的关系图如图10。管道底部最大等效应变与管道埋深的关系图如图11。

图10 最大等效应变与管道埋深关系(管顶)

图11 最大等效应变与管道埋深关系图(管底)
管道顶部的最大等效应变受管道埋深的影响,因冻胀段长度的不同,情况不同。在冻胀段长度处于10~15 m时,管道顶部受到上覆土的压力随着埋深的增加而加大,逐渐超过管道受到的土壤因冻胀对其的向上的径向力,因此出现了管顶应变减小的情况;在冻胀段长度为20~30 m时,上覆土给管顶向下的压力始终比土壤给管道径向向上的冻胀力大,因此管顶应变在此时呈增长趋势,见图12。
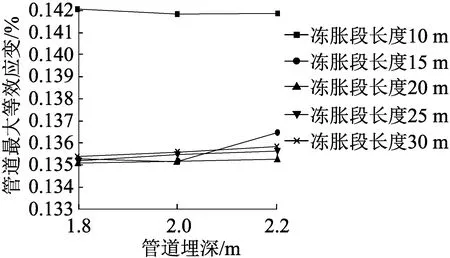
图12 管道最大等效应变与管道埋深关系
结合前文,整理得到管道最大等效应变随管道埋深的关系图如图12所示。在冻胀段长度为10 m时,管道应变随着埋深的增加先增大后不变,在冻胀段长度为15 m时,管道应变随着埋深的增加呈现先减后增的趋势,在冻胀段长度为20~30 m时,管道应变随着埋深的增加而增大,见表4。

表4 管道埋深对管道应变的影响 %
如表4所示,在埋深为1.8~2.0 m时,冻胀段长度为10 m的管道,管道最大等效应变减小幅度最大,降幅约为0.140 7%;管道应变最大增幅为0.886 7%,发生于埋深为2.0~2.2 m,冻胀段长度为20 m的管道,土体冻胀段长度使管道应变变化可达4.79%,而管道埋深对管道应变的影响最大仅有0.886 7%,因此管道埋深对管道变形的影响没有冻胀段长度对管道的影响强烈。
3.3 管道壁厚对管道最大等效应变的影响
保持管道埋深为1.8 m不变,改变管道壁厚,分析了12.5 mm、14.2 mm和16 mm 3种管道壁厚,冻胀段长度分别设置为10、15、20、25 m和30 m。管道顶部的最大等效应变与管道壁厚的关系图如图13,管道底部最大等效应变与管道壁厚的关系图如图14。
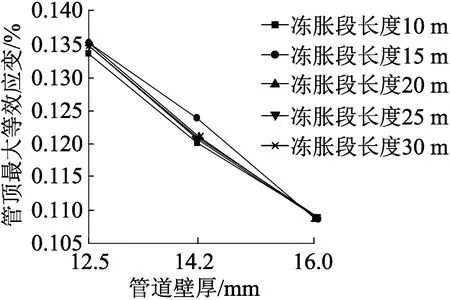
图13 最大等效应变与管道壁厚关系(管顶)
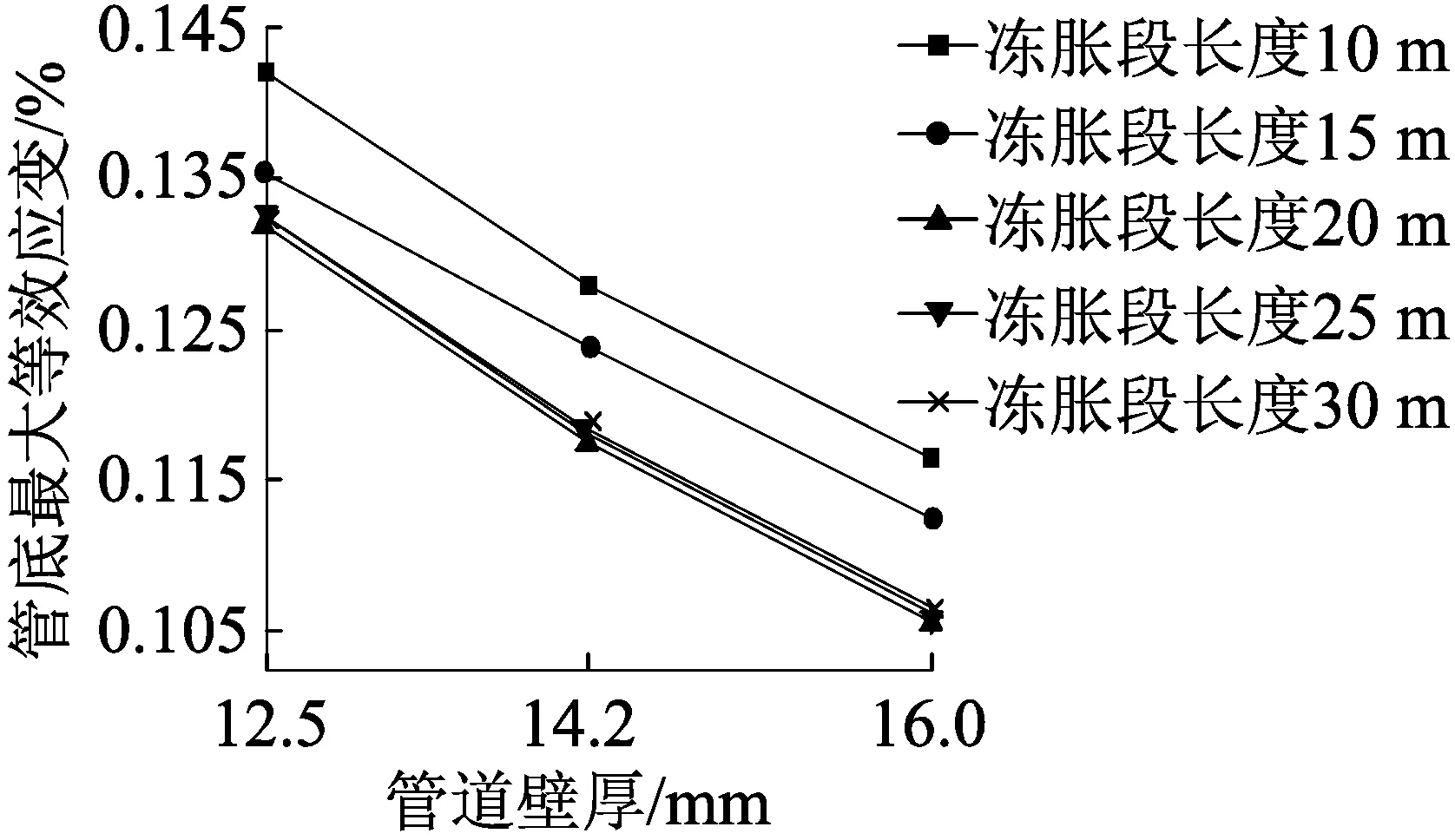
图14 最大等效应变与管道壁厚关系(管底)
从图13中可以清楚看出,管道顶部最大等效应变随管道壁厚的增加而降低,且对不同冻胀段长度,管顶最大等效应变值的大小差别不大,仅有冻胀段长度为15 m时,在管道壁厚为14.2 mm时,管顶应变值比其他情况下的应变值略大。
管底的最大等效应变随管道壁厚的变化如图14所示,与管顶应变变化的趋势一样,管底最大等效应变与管道壁厚增长成反比。与管顶应变值不同,管底应变值在冻胀段长度处于10 m和15 m时明显大于其他情况下的应变值。
综合上述管顶和管底的应变变化情况,图15所示为管道应变与管道最大等效应变的关系图。从图中可以看出,管道最大等效应变随着管道壁厚的增加而减小。这是由于在同等情况下,管道壁厚增加,管道因土体冻胀导致的变形稍稍变小,因此管道的最大等效应变与管道壁厚增加成反比。

图15 管道应变与管道最大等效应变的关系
管道应变具体参数如表5。在管道壁厚为12.5 mm,冻胀段长度为10 m时,管道应变值最大为0.142 1%。在冻胀段长度为20 m,管道壁厚为12.5~14.2 mm时,管道应变变化幅度最大,管道应变从0.135 1%减小为0.120 7%,此时应变降幅为10.83%。

表5 管道壁厚对管道应变的影响 %
4 结论与展望
本章通过建立不同的管-土相互作用三维模型,对比分析不同影响参数对管道的影响,结果表明:
(1)在管道壁厚不变的情况下,管道埋深对管道应变的影响,随冻胀段长度不同。在冻胀段长度为10 m时,管道应变随着埋深的增加先增大后不变,在冻胀段长度为15 m时,管道应变随着埋深的增加呈现先减后增的趋势,在冻胀段长度为20~30 m时,管道应变随着埋深的增加而增大。
(2)冻土区冻胀条件下,管道壁厚是对管道应变影响最大的参数,其次是冻胀段长度,管道埋深对管道应变的影响极小。通过对不同冻胀段长度、管道埋深和管道壁厚模型的分析计算,管道应变最大值一般都发生在冻胀段长度小于15 m的情况下。因此在敷设冻土区管道时,为保障管道的安全运行,应该避免小型的块状冻层区域。
