基于AMPSO算法的船舶工业喷涂机器人喷涂参数优化

马淑梅,罗 曦,李爱平,周韵文

(同济大学 机械与能源工程学院,上海 201804)



基于AMPSO算法的船舶工业喷涂机器人喷涂参数优化

马淑梅,罗 曦,李爱平,周韵文

(同济大学 机械与能源工程学院,上海 201804)

针对船舶工业喷涂机器人喷涂参数即喷涂速度、喷涂高度和喷涂轨迹间距的优化问题,提出一种基于自适应变异粒子群算法(Adaptive Mutation Particle Swarm Optimization,AMPSO)的喷涂参数优化方法,实现了喷涂质量最佳和喷涂效率最高的目标.通过分析喷涂参数与膜厚的关系,基于现有模型建立膜厚叠加分布模型,根据优化目标,以膜厚要求和机器人作业能力为约束条件得到最优喷涂参数.通过对船舶分段外表面喷涂仿真,并与标准粒子群优化算法比较,改善了传统算法早熟收敛问题,验证了算法的有效性和合理性.

喷涂机器人; 喷涂参数优化; 粒子群算法; 船舶工业

在船舶工业中喷涂机器人在不同喷涂参数下具有不同的膜厚分布模型及喷涂轨迹,喷涂参数的优化也包含这两个方面.其中,漆膜厚度分布模型用于描述覆盖范围内各点处膜厚值分布,喷涂轨迹是机器人为完成喷涂作业需要移动的路径.因此喷涂参数的选择将影响喷涂质量和效率,对生产有重要意义.

近年来对喷涂参数优化的研究中,漆膜厚度分布模型方面,ARIKAN[1]等研究了被广泛使用的漆膜厚度β分布模型,SUH[2]等人提出漆膜厚度的平面高斯分布模型但精度不高,张永贵[3]基于β模型推广得到椭圆双β分布模型等,但他们均未对喷涂轨迹进行深入研究;在喷涂轨迹规划方面,陈伟等[4]针对分片喷涂轨迹优化问题研究两片交界处喷枪路径的位置关系,李发忠等[5]推导自由曲面上漆膜累积速率函数,并通过遗传算法求解问题,邵振华等[6]研究了规则化曲面喷涂轨迹规划问题,对各不同规则化曲面的喷涂轨迹优化进行研究,但是他们未深入研究漆膜厚度分布模型.因此上述学者在喷涂参数优化方面没有综合考虑漆膜厚度分布模型和喷涂轨迹对喷涂参数的影响,且采用的遗传算法更适合优化离散问题.

针对上述问题结合船舶工业实际,本文综合考虑漆膜厚度分布模型和轨迹规划问题,研究喷涂机器人对船体分段外表面喷涂时的参数优化.基于漆膜厚度β分布模型,考虑喷涂速度、喷涂高度和喷涂轨迹间距与膜厚分布的关系建立新模型.以实际问题为约束条件,以喷涂效率和喷涂质量最佳为目的,运用AMPSO优化得到合适的喷涂参数,最终提高机器人喷涂作业的效率并改善喷涂质量.

1 漆膜叠加厚度分布模型的建立

漆膜厚度分布模型用于获取各点处膜厚值,为得到符合优化目标的喷涂参数,必须建立一个精度较高的模型用于优化参数.

1.1 改进已有膜厚分布模型

本文以β分布模型作为漆膜厚度分布模型讨论,图1为喷涂示意图,图中漆膜覆盖区域半径为r,喷嘴雾幅张角为,喷涂距离为h.漆膜厚度在x轴方向的分布遵循β分布模型,膜厚分布公式[7]如下:

(1)

式中:Q0为喷漆流量;为喷涂区域宽度;v为喷枪移动速度,β为无具体物理意义参数.

等式(1)所表示的模型更多地是用来拟合现有的漆膜厚度,而不能预测不同参数下膜厚分布情况.针对这一缺点,下文将阐述对该模型的改进.

图1 不同高度单喷嘴喷涂示意图Fig.1 Single painting stroke in different height

Q0和只与喷嘴型号有关,因此喷嘴型号不变时和h之间的关系,在图1中可以表示为.而当Q0不变时,喷涂面积随高度增加而扩大,不同高度对应点处(图1中x1和x2)膜厚关系可以表示为2, T1,T2分别表示h1,h高度时膜厚分布情况.

当喷嘴型号和h不变时,T(x)和v成反比.对同种型号喷嘴,首先选定基准喷涂速度和喷涂距离hs,测量膜厚值及此时漆膜覆盖宽度s,确定基准膜厚分布模型;再通过等式(1)和不同高度膜厚关系式,推导非基准条件下膜厚分布,使改进后的模型能预测膜厚分布.把运用改进后模型(式(2))得到的预测数据与试验数据对比,得出23个点处膜厚平均误差为5.08%,因此该模型具备可行性.

(2)

式中:T′(x),v′,h′分别是非基准状态下漆膜厚度、喷枪移动速度和喷涂距离.

1.2 建立漆膜叠加厚度分布模型

实际喷涂作业中,相邻两道漆膜存在叠加部分,该部分膜厚值对整体膜厚均匀程度有重大影响,因此需要建立叠加模型优化相邻轨迹间距.根据试验得到基准状态下hs=35 cm,s=71 cm,β=3.5,则T(x):

(3)

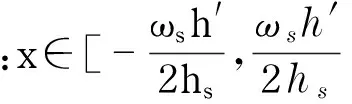
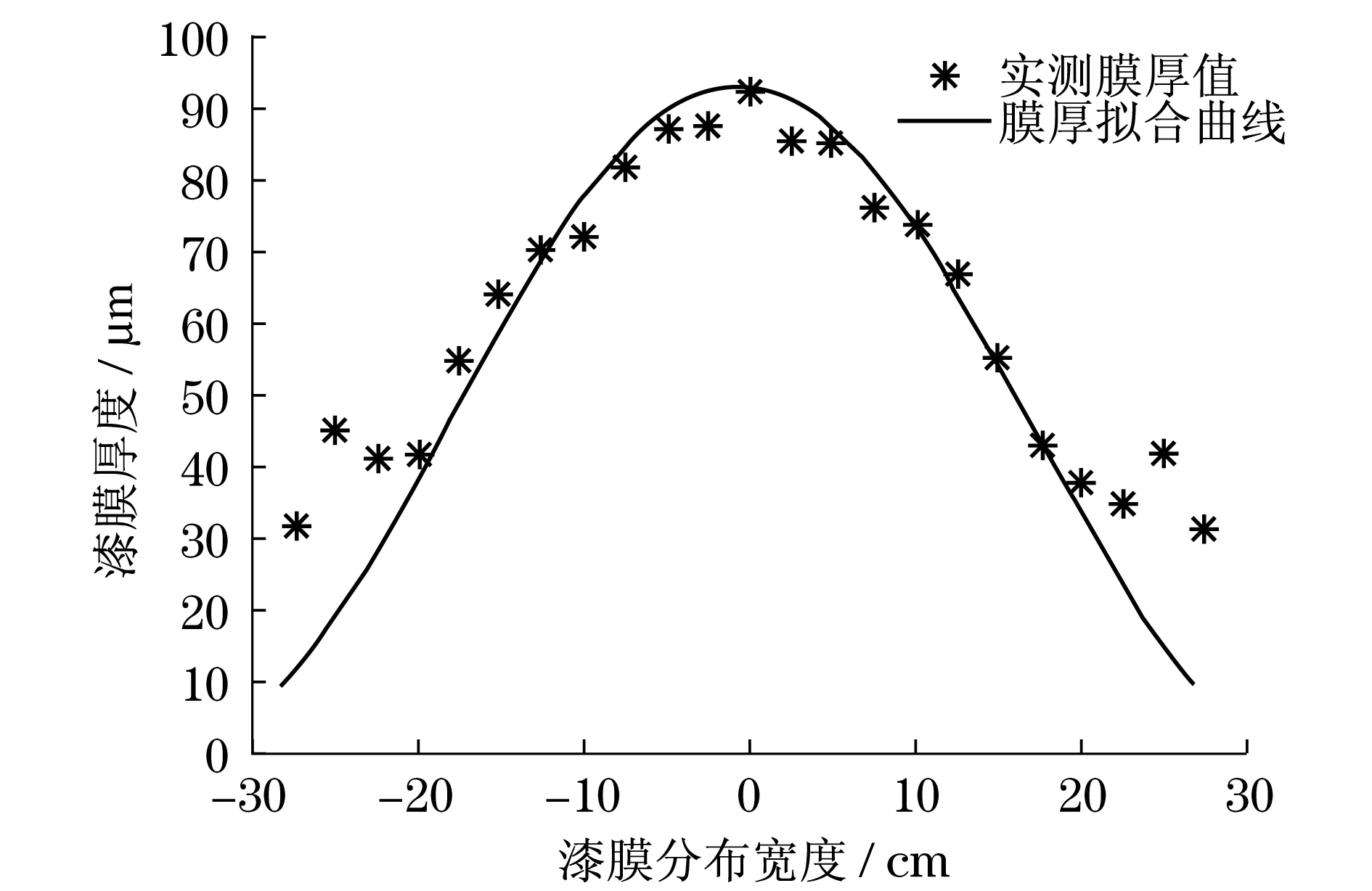
图2 基准状态下实测膜厚与拟合膜厚分布Fig.2 Experimental and fitting thickness curves in standard condition

图3 平面喷涂轨迹Fig.3 Schema of painting trajectory

图4 叠加膜厚示意图Fig.4 Overlapped thickness

通过以上分析,漆膜叠加厚度分布模型Td(x)表达式可以表示为

(4)

2 基于AMPSO算法的喷涂参数优化问题求解

根据所得漆膜叠加厚度分布模型,为了在约束条件范围内求解出符合目标函数的喷涂参数,本文采用AMPSO算法进行优化.

2.1 目标函数

(1) 喷涂质量函数

喷涂质量是指机器人作业后,整个漆膜覆盖范围内漆膜厚度的均匀程度.机器人在喷涂过程中按规划的轨迹运动,在任意相邻两道油漆之间有叠加部分,而叠加区域的宽度将影响膜厚均匀程度,因此,在设置喷涂质量函数时,选取叠加区域膜厚作为研究对象,取膜厚的方差作为评价指标fq,其表达式为

(5)

(2)喷涂效率函数

喷涂效率是指机器人完成所有喷涂任务所需要耗费的时间.在确保喷涂质量的同时,若提高喷涂效率有利于企业缩短制造周期降低成本.在长为L宽为W的待喷涂区域中,喷涂效率函数fe如下:

(6)

式中:t为喷涂时间;n为喷漆覆盖整个喷涂区域所需喷涂次数,表达式所得n值若为小数则向上圆整.

2.2 约束条件

在喷涂机器人参数优化中,约束条件主要包括漆膜厚度要求,机器人作业能力约束等.

为了满足船东对船舶防腐蚀能力的要求(Tmin),同时兼顾企业效益(Tmax),因此膜厚应满足Tmin≤T≤Tmax;根据机器人作业能力(vmax),并避免机器人频繁加减速,保证喷涂效率(vmin),因此速度约束为vmin≤v≤vmax;由于当前所使用爬壁式喷涂机器人,在机器人运动时,相邻轨迹相隔过近可能导致机器人碾压油漆,因此限定喷涂轨迹间距>min.

2.3 算法选用

粒子群算法(Particle Swarm Optimization,PSO)由Kennedy和Eberhart提出用于解决大规模优化问题,具有收敛速度快、全局寻优能力强等特点.

粒子群中每个粒子代表一个可能解,粒子具有位置和速度两个特征.粒子通过迭代寻找最优解,每次迭代时粒子通过跟踪个体极值和全局极值更新速度和位置[],更新公式如下:

(7)

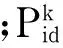
(8)

PSO运行速度快,但易陷入早熟收敛.因此引入变异操作,根据群体适应度值的方差σ2及当前最优解的大小确定当前最优粒子的变异概率Pk[9].适应度值方差σ2体现了粒子群中所有粒子的收敛程度,σ2越大表明粒子群处于随机搜索状态,反之则趋向收敛,变异概率计算公式如下:

(9)

(10)

AMPSO实际上是在PSO的基本框架中增加了随机变异算子,通过对全局极值的随机变异来提高PSO跳出局部最优解的能力,不仅有很强的全局搜索能力,而且能有效避免PSO的早熟收敛问题.

2.4问题求解流程

基于AMPSO算法的喷涂参数优化问题求解流程如图5所示:

图5 AMPSO流程图Fig.5 Flow chart for AMPSO

具体过程如下:

(1) 确定待优化参数取值区间,随机初始化粒子群中粒子的位置和速度.

(2) 根据所取的适应度函数计算初始粒子群的适应度值.

(3) 将粒子群当前位置设置为初始粒子群中最佳粒子位置.

(4) 将粒子群中所有粒子进行如下操作:①根据式(7)和(8)更新粒子的速度和位置;②若粒子适应度值好于的适应度,则设为新位置;③若粒子适应度值好于的适应度,则设为新位置.

(5) 计算群体适应度方差,并根据等式(9)计算变异概率Pk.

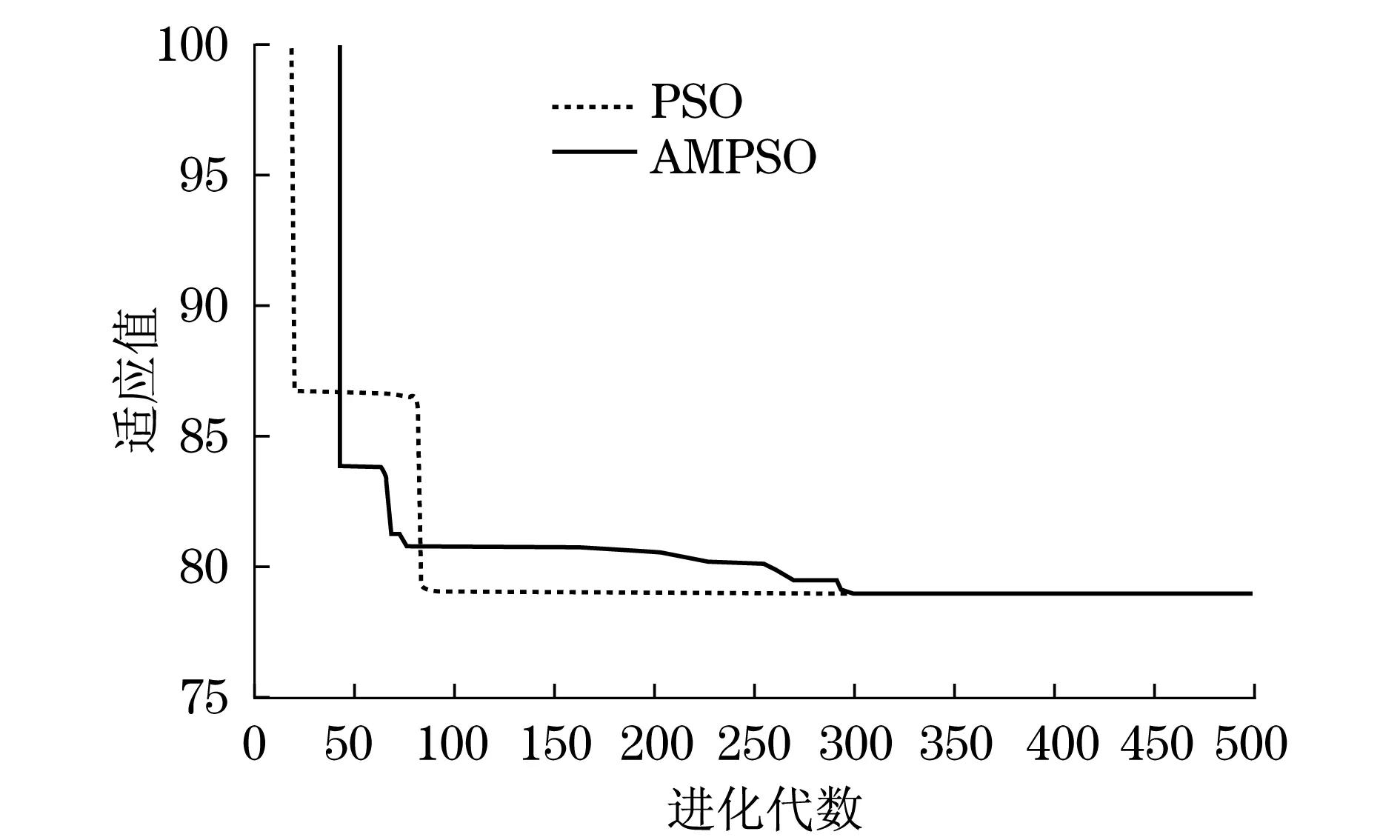
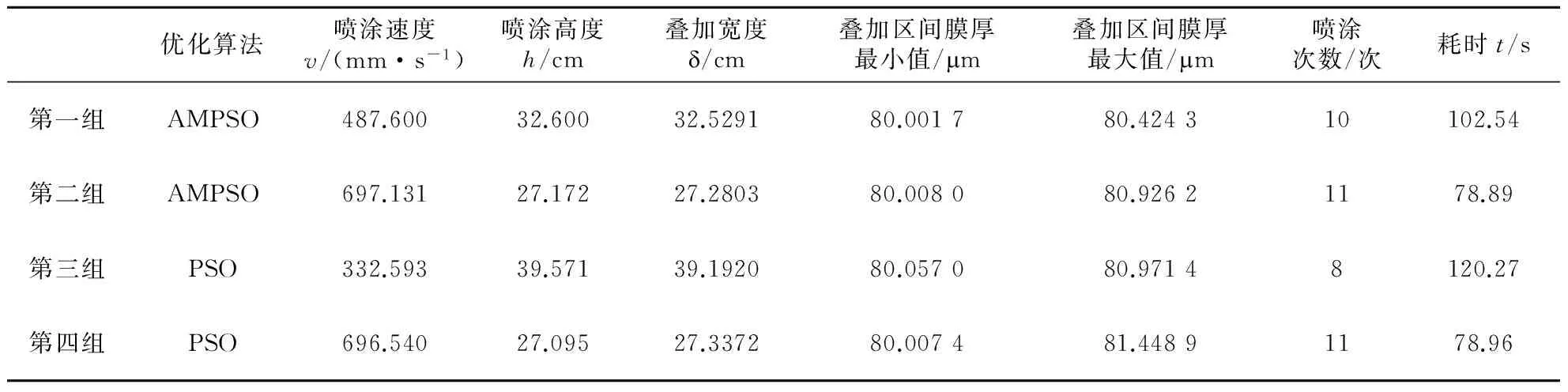
(6) 生成随机数r,若r

(7) 判断是否满足终止条件,若是,转向步骤8,否则转向步骤4.

(8) 输出,结束.

3 实例仿真及结果分析

3.1 实例仿真

本文依托“面向大型船舶的智能喷涂机器人研发及应用”等项目的实施,研究喷涂机器人在船体外表面喷涂问题.为了模拟机器人在船体分段上的喷涂作业,本文采用长5 m宽3 m的平板模拟分段,并要求85 μm>T>80 μm,>10 cm,100 mm·s-1

由前文所述,设置种群粒子数n=100,Gmax=500,wmax=0.95,wmin=0.4,c1=c2=1.494 45,Pmax=0.4,Pmin=0,粒子维度为3.经AMPSO优化分别得到两组参数:第1组v1=487.6 mm·s-1,h1=32.6 cm,1=32.529 cm;第2组v2=721.232 mmη,h2=26.7998 cm,2=26.7421 cm.两组参数对应的膜厚如图6所示.

图6 第1、2组参数喷涂膜厚示意图(两道叠加)Fig.6 Schema of thickness distribution of Set 1 and Set 2 parameters(two strokes overlapped)

作为对比,采用PSO算法对喷涂参数优化,优化得到第3组参数v3=332.593 0 mm·s-1,h3=39.570 7 cm,3=39.192 0 cm;第4组v4=683.680 6 mm·s-1,h4=27.555 0 cm,4=27.283 7 cm,算法适应度值如图7所示.

图7 算法适应度值对比Fig.7 Fitness value of PSO and AMPSO

3.2 结果分析

4组优化值的相关参数对比如表1所示:

表1所示采用4组优化参数喷涂的膜厚均能满足生产要求.比较不同优化目标,第1组和第3组参数喷涂时,在膜厚均匀性方面分别好于第2组和第4组参数;第2组和第4组参数喷涂时,喷涂次数虽有所增加,但耗时明显小于第1组和第3组参数,喷涂效率分别提高了23.06%和34.34%.

表1中AMPSO和PSO优化后喷涂参数的喷涂质量和喷涂效率两方面比较,第1组参数的膜厚均匀性和喷涂效率均好于第3组参数,第2组参数的喷涂效率略优于第4组参数,且膜厚均匀性也好于第4组参数.由图5(b)可知,在优化得到第2组和第4组参数时,PSO算法在第80代收敛,而AMPSO需要403代时才得到最优个体.因此,虽然AMPSO的运算量大于PSO,但优化结果好于PSO,从参数优化的结果比较,AMPSO好于PSO,而从运算效率来看,PSO要好于AMPSO.

表1 喷涂参数优化对比

4 结语

本文针对船舶工业喷涂机器人喷涂参数优化问题,建立可预测不同喷涂参数下膜厚分布的漆膜厚度分布模型并完善膜厚分布表达式;引入AMPSO根据船舶工业喷涂作业特点设置优化目标及约束条件,得到机器人最优喷涂参数组合,通过实例仿真验证了参数合理性;采用文中方法结合船舶工业生产实际,将得到不同型号喷嘴对应的膜厚分布公式,减少获取最优喷涂参数所需的试验次数,降低企业生产成本.

[1] ARIKAN M A S,BALKAN T.Process modeling,simulation,and paint thickness measurement for robotic spray painting[J].Journal of Robotic Systems,2000 (17): 479-494.

[2] SUH S H,WOO I K,NOH S K.Development of an automatic trajectory planning system (ATPS) for spray painting robots[C]//Proceedings of IEEE International Conference on Robotics and Automation，Piscataway:IEEE,1991:1948-1955.

[3] 张永贵.喷漆机器人若干关键技术研究[D].西安: 西安理工大学,2008.

ZHANG Yonggui.Study on some key techniques tor spray-painting robot[D].Xi′an：Xi′an University of Technology,2008.

[4] 陈伟.喷涂机器人轨迹优化关键技术研究[D].镇江: 江苏大学,2012.

CHEN Wei.Research on key techniques of robotic spraypainting trajectory optimization[D].Zhenjiang:Jiangsu University,2012.

[5] 李发忠,赵德安,姬伟,等.面向凹凸结构曲面的喷漆机器人轨迹优化研究[J].江苏科技大学学报:自然科学版,2008,22(4):64-67.

LI Fazhong,ZHAO De'an,JI Wei,et al.Trajectory optimization of spray painting robot for concavo-convex surfaces[J].Journal of Jiangsu University of Science and Technology:Natural Science,2008,22(4):64-67.

[6] 邵振华,周波,孟正大,等.针对规则化工件曲面的喷涂轨迹规划研究[J].计算机技术与发展,2015,25(3):6-10.

SHAO Zhenhua,ZHOU Bo,MENG Zhengda,et al.Research on path planning of spray paint-ing for standardized workpiece[J].Computertechnologyanddevelopment,2015,25(3):6-10.

[7] 魏士博.喷漆漆膜厚度控制算法研究及优化[D].武汉: 武汉理工大学,2013.

WEI Shibo.Painting film thickness control algorithm research and optimization[D].Wuhan:Wuhan University of Technology,2013.

[8] KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks，Piscataway:IEEE,1995: 1942-1948.

[9] 吕振肃,侯志荣.自适应变异的粒子群优化算法[J].电子学报,2004,32(3): 416-420.

LÜ Zhensu,HOU Zhirong.Particle swarm optimization with adaptive mutation [J].Acta Electronica Sinica,2004,32(3): 416-420.

Painting parametric optimization using AMPSO algorithm on ship painting robots

MA Shu-mei,LUO Xi,LI Ai-ping,ZHOU Yun-wen

(College of Mechanical Engineering,Tongji University,Shanghai 201804,China)

Optimize the painting velocity,height and trajectory pitch,an optimization approach is proposed based on adaptive mutation particle swarm optimization (AMPSO) algorithm to realize best painting quality and efficiency.Based on the film thickness distribution model (FTDM),the relationship between the parametersand film thickness is proposed.By establishing the overlapped FTDM,the film thickness and robot working capacity is treated as constraints.By simulating the robot painting process on ship outer surfaces and comparing with the traditional PSO algorithm,the validity and rationality of AMPSO are verified,whereas such weaknesses of PSO algorithm as premature convergence can be improved.

painting robot; painting parametric optimizing; PSO algorithm; shipbuilding industry

上海经信委资助项目(沪CXY-2013-25)；上海科委资助项目(14111104400).

马淑梅(1968-)，女，副教授.E-mail：mashumei@tongji.edu.cn

TP 242.2

A

1672-5581(2016)02-0125-06