基于改进的R-O模型模拟U型软钢阻尼器滞回曲线研究
2016-12-12段言彪杜红凯
韩 淼, 段言彪, 杜红凯
(北京建筑大学 土木与交通工程学院 北京节能减排关键技术协同创新中心, 北京 100044)
基于改进的R-O模型模拟U型软钢阻尼器滞回曲线研究
韩 淼, 段言彪, 杜红凯
(北京建筑大学 土木与交通工程学院 北京节能减排关键技术协同创新中心, 北京 100044)
为模拟U型软钢阻尼器荷载- 位移滞回曲线,根据软钢R-O模型应力- 应变曲线方程,推导出弹性条件下荷载- 位移曲线方程. 引入塑性变形影响参数α,给出弹塑性条件下荷载- 位移曲线方程. 根据Masing准则给出U型软钢阻尼器荷载- 位移滞回曲线方程. 进行四种U型软钢阻尼器的拟静力试验,对塑性变形影响参数α回归分析,得到基于改进R-O模型的荷载- 位移滞回曲线模拟方程. 对比模拟方程绘制的滞回曲线与试验滞回曲线,二者吻合良好.
U型软钢阻尼器; 滞回曲线; 改进的R-O模型; 骨架曲线; 塑性变形
工程结构隔震、减震及振动控制方面的研究一直备受国内外学者关注,并且取得大量研究成果,改变了传统建筑结构靠强化自身抵抗地震作用的设计理念[1-5].
软钢阻尼器因其构造简单、施工简便、造价低廉、耗能性能良好等特点被广泛关注. 国内外已研发了多种不同耗能理念及形式的阻尼装置,如:U型软钢阻尼器、开孔式加劲软钢阻尼器、双环软钢阻尼器、抛物线外形软钢阻尼器、X型软钢阻尼器、三角形软钢阻尼器[6-10]等. 它们一般安装在结构的节点、剪力墙、联结缝、或楼层之间,通过塑性变形来耗散地震动输入结构的能量,以减小结构的反应.
U型软钢阻尼器的研究多集中在加载刚度、卸载刚度、切线刚度、割线刚度、骨架曲线等方面,缺少滞回曲线方程的相关研究. 本文根据U型软钢阻尼器(如图1、图2)荷载- 位移滞回曲线饱满、没有捏拢现象的特点,运用 Ramberg和Osgood[11]提出的应力- 应变骨架曲线R-O模型及Masing准则,对其荷载- 位移滞回曲线进行理论推导及试验研究.
1 滞回曲线方程推导
1.1 R-O基本模型及Masing准则
R-O模型方程用于描述材料的应力- 应变关系,但在U型软钢阻尼器力学性能分析中,直接使用的是荷载- 位移关系. 现将R-O模型方程的应力- 应变关系方程转化成荷载- 位移关系方程.
R-O模型应力- 应变曲线是将软钢材料的应力- 应变曲线等效为光滑曲线,其骨架曲线如图3所示. 一般形式的R-O模型数学方程如下[12]:
(1)
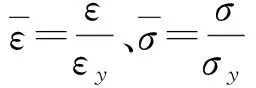
Masing准则的特点是骨架曲线和滞回曲线都是光滑的,它的一般形式是:设恢复应力的光滑骨架曲线为σ0(x),则卸载或再加载时的滞回曲线满足式(2)[13],Masing模型代表的光滑滞回曲线如图3.
(2)
以上式中:σ和ε为某一滞回曲线上的坐标;σr和εr为加载过程中卸载点的应力应变值. 若每次都在滞回曲线顶点处卸载,如图3中点1、2、3、4、5、6,则σr=σ或-σ;εr=ε或-ε.
文献[14]给出了软钢材料R-O模型无量纲形式的骨架曲线方程:
(3)
1.2 U型软钢阻尼器改进的R-O模型荷载- 位移滞回曲线方程
U型软钢阻尼器可简化为受弯钢板[15]158-163,根据其危险截面的受力特点应力分布如图4,应变简化如图5.
在弹性和弹塑性阶段都满足关系ε=κy.κ为中性界面曲率. 存在关系式ε=εe+εp,κ=κe+κp,那么有:
(4)
由式(4)可得:
(5)
将式(5)带入到式(3)得到:
(6)
(7)
(8)
由于U型软钢阻尼器加载过程中存在屈服和卷曲现象,在式(8)中引入塑性变形影响系数α,得到弹塑性条件下荷载- 位移骨架曲线方程及其无量纲形式如下:
(9)
式(9)由Masing准则得荷载- 位移滞回曲线方程:
(10)
其中,P*、Δ*分别是每次卸载处的荷载和位移,P、Δ分别是加载过程荷载和位移.
2 U型软钢阻尼器试验概况
2.1 试件设计及制作
U型软钢阻尼器的设计参数包括:钢板厚度t,宽度b,弯曲段中心线圆弧半径R,平直段长度L,阻尼器构造如图1所示. 设计弯曲段中心线圆弧半径R=100 mm,L为150 mm,200 mm,钢板厚度t取10 mm,16 mm,宽度b取80 mm,160 mm. 将设计参数组合,共有4种类型U型钢板,每种加工4个,共16个阻尼器,其尺寸组合见表1. 阻尼器采用钢板直接热弯加工而成,未进行回火处理.
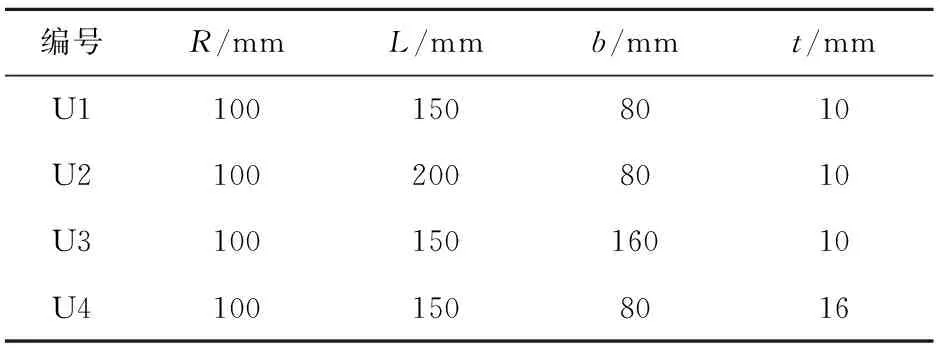
表1 U型软钢阻尼器设计参数
2.2 试验装置及加载制度
阻尼器试验装置采用MTS公司生产的伺服作动器施加水平力,试验装置示意图如图6所示. 千斤顶通过加载板对U型软钢阻尼器施加水平推力,阻尼器与固定板通过螺栓连接. 加载板与底座之间垫有滚轴以减小两者之间的摩擦.
加载为水平静力循环加载(如图7),加载制度分四级,采用位移控制,最大加载位移为U型钢板的圆弧段半径R(100 mm),加载位移极值分别为10 mm,25 mm,50 mm,100 mm,加载速度分别为0.1 mm/s,0.25 mm/s,0.5 mm/s,1 mm/s,每级加载至最大位移后开始卸载,卸载至反力为0再反向加载至最大位移. 每个循环加载均进行一次,然后进行下一级加载. 最后一级卸载完毕后结束试验.
3 试验现象及结果分析
3.1 试验现象
加载过程中U型阻尼器随位移增大出现明显的塑性变形和卷曲现象. 当加载位移较大时卸载后出现明显的残余变形,循环加载过程中阻尼器表现出良好的变形能力.
3.2 滞回曲线及数据
循环加载测得每种阻尼器两条滞回曲线基本完全重合,任选每种阻尼器一条滞回曲线,如图8、图9、图10、图11. 由滞回曲线可知,所有试件的荷载- 位移曲线形状相似,滞回环平滑、饱满,未出现捏拢现象. 在加载位移较小时阻尼器处于弹性阶段,当位移达到一定值时阻尼器进入弹塑性阶段,卸载后出现明显的残余变形. 说明此类限位器具备良好的延性及耗能能力.
表2给出四种阻尼器的屈服荷载Py及屈服位移Δy,以及各级加载下极值位移Δ*对应的荷载值.
3.3 塑性影响参数α回归分析
将试验所得数据用公式(10)对α进行回归分析,得到如下规律:
1) 循环加载过程中,从极值点卸载到反向加载至另一个极值点α的变化规律一致(图12).
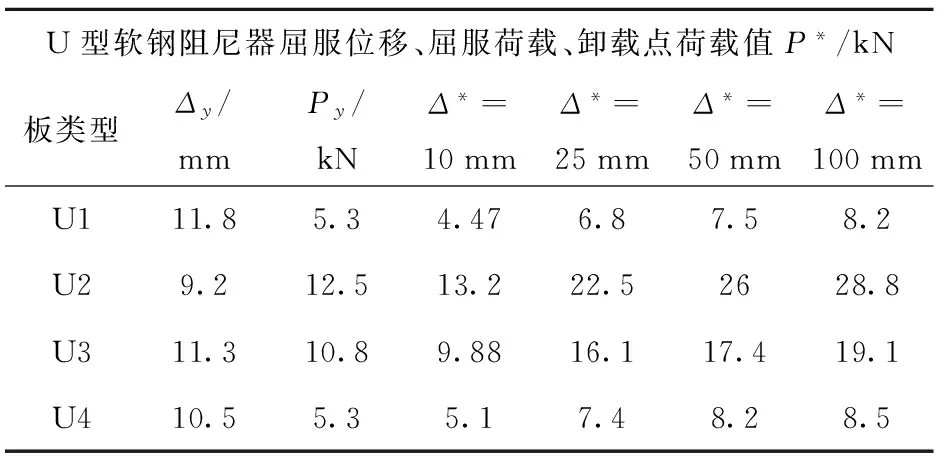
表2 U型软钢阻尼器试验数据
2)α值在加载过程中出现明显拐点,卸载前期α值变化幅度大,后期变化平缓.
3)α值变化趋势整体可分为两阶段,第一段为明显递减段. 第二段为平滑阶段,α值呈较小的递减趋势.
依据以上规律将α值分段与荷载分段P建立关系. 对所有试验数据进行分析发现,α拐点出现在0.25P*附近. 第一段取为P*~0.25P*、第二段为0.25P*~-P*. 将P与α关系进行拟合,第一段用指数函数拟合,第二段用线性公式拟合. MATLAB计算表明两段内参数α和荷载P拟合方程曲线与试验曲线重合的置信区间介于95%~99%(表3). 以下是拟合公式(12)和部分拟合曲线(图13,图14):
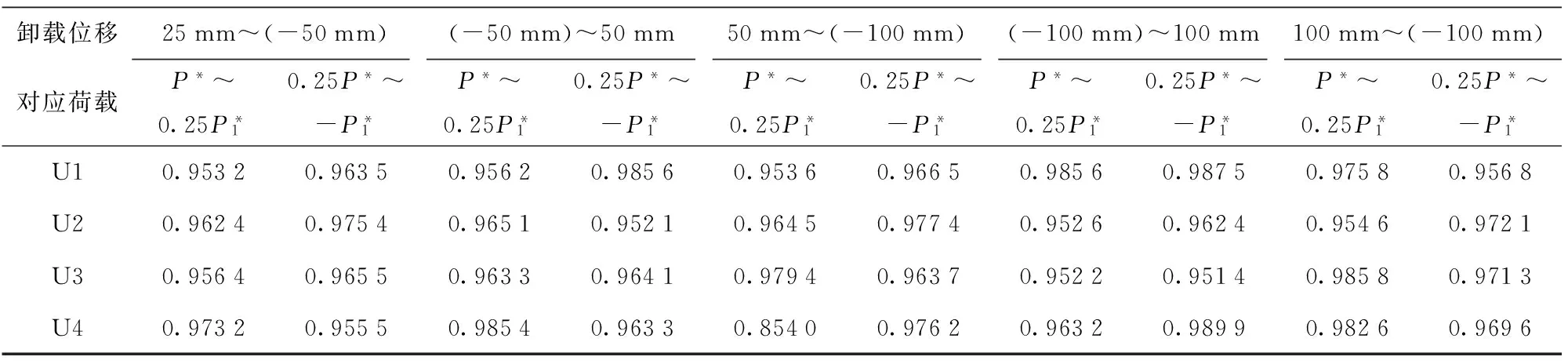
表3 参数α拟合曲线与试验曲线重合率
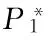
对应方程为:
若卸载点为正值:
(11)
若卸载点为负值:
(12)
将方程(11)和方程(12)对应带入到方程(10),得到U型软钢阻尼器改进的R-O模型滞回曲线试验方程.
在MATLAB中用改进的R-O模型编写程序绘制荷载- 位移滞回曲线及骨架曲线. 图15、图16给出了U3软钢阻尼器的对比图. 比较发现骨架曲线和改进后的R-O模型滞回曲线与试验曲线吻合的良好.
4 结论
本文推导出U型软钢阻尼器的荷载- 位移滞回曲线方程,并进行U型软钢阻尼器拟静力试验. 对参数α进行回归分析,将试验曲线与模拟曲线进行了对比. 得到如下结论:
1) 根据R-O模型应力- 应变曲线方程及Masing准则,引入塑性变形参数α,推导出U型软钢阻尼器改进的R-O模型荷载- 位移滞回曲线方程.
2) 通过对四种U型软钢阻尼器拟静力试验得到试验荷载- 位移滞回曲线. 用试验数据对塑性变形影响参数α进行回归分析,发现塑性变形影响参数α随荷载变化规律,给出塑性变形参数α与荷载P的拟合方程. 拟合方程曲线与试验曲线重合的置信区间介于95%~99%.
3) 用U型软钢阻尼器改进的R-O模型荷载- 位移滞回曲线方程绘制滞回曲线,与试验滞回曲线对比,吻合良好.
[1] 韩淼,周锡元.基础隔震建筑软碰撞保护分析[J].建筑科学, 1999, 15(1): 14-20
[2] Nagarajaiah S, Sun X H. Base-isolated FCC building: impact response in northridge earthquake [J]. Journal of Structural and Engineering, 2001,127(9):1063-1075
[3] Hsiang-Chuan Tsai.Dynamic analysis of base-isolated shear beams bumping against stops [J]. Earthquake Engineering and Structural Dynamics, 1997, 26(5): 515-528
[4] Matsagar V A, Jangid R S. Seismic response of base-isolated structures during impact with adjacent structures [J]. Engineering Structures, 2003, 25(12): 1311-1323
[5] Masroor A, Mosqueda G. Impact model for simulation of base isolated buildings impacting flexible moat walls [J]. Earthquake Engineering and Structural Dynamic, 2013, 42(3): 357-376
[6] 张文元,张敏政,李东伟.新型加劲软钢阻尼器性能与试验[J].哈尔滨工业大学学报,2008(12):1888-1894
[7] 徐艳红,李爱群,黄镇.抛物线外形软钢阻尼器试验研究[J].建筑结构学报,2011(12):202-209
[8] 李宏男,李钢. 双X型软钢阻尼器[P]. 中国专利:CN200410020892.8,2004-10-02
[9] Whittaker A S, Bertero V V,ThomPson C I, et al. Seismic testing of steel plate energy dissipation devices [J]. Earthquake Spectra,1991, 7(4):563-604
[10] Tsai K C, Chen H W, Hong C P,et al. Design of steel triangularl plate energy absorbers for seismic-resistant construction[J]. Earthquake Spectra,1993, 9(3):505-528
[11] 徐灏.疲劳强度[M].北京:高等教育出版社,1988:25-53,215-236
[12] 欧进萍,王光远.结构随机振动[M].北京:高等教育出版社,1998:261-308
[13] Suregh S.材料的疲劳[M].王中光,等,译.北京:国防工业出版社,1999:51-80
[14] Cofie N G, Krawingler H. Unixial cyclic stress-strain behavior of structural steel[J]. J. Enger Mech ASCE,1985,111(9): 11105-11120
[15] 杜红凯, 韩淼, 闫维明. 约束U形钢板力学性能的计算方法研究[J]. 土木工程学报, 2014,47(S2):158-163
[责任编辑:佟启巾]
Analysis of Simulating Hysteresis Curve of U-Shape Mild Steel Damper Based on the Improved R-O Model
Han Miao, Duan Yanbiao, Du Hongkai
(School of Civil and Traffic Engineering, Beijing Cooperative Innovation Research Center for Energy-Saving and Emission Reduction, Beijing University of Civil Engineering and Architecture, Beijing 100044)
In order to simulate the U-shape mild steel damper hysteretic curves, according to the R-O model of mild steel stress-strain curve equation,the condition of elastic displacement of force-displacement curve equation is derived. The plastic deformation parameterαis introduced, and the force-displacement curve equation is given under the condition of elastic and plastic. U-shape mild steel damper the force-displacement hysteresis curve equation is derived by using the Masing rules. For four kinds of U-shape mild steel damper quasi static test, the simulation equation of force-displacement hysteresis curve based on improved R-O model is obtained by the regression analysis of the influence parameters of plastic deformation. Compared the simulated hysteresis curves and experimental hysteresis curves, the two are in good agreement.
U-shape mild steel dampers; hysteresis curve; improved R-O model; skeleton curve; plastic deformation
1004-6011(2016)03-0043-06
2016-07-20
国家自然科学基金项目(51378047,51408027)
韩 淼(1969—),男,教授,博士生导师,博士,研究方向:工程结构抗震减灾及抗震性能研究.
TU352.1+1
A
