倒立摆系统基于能量控制的起摆控制策略研究
2016-12-10曹茂永
高 皜,曹 琳,曹茂永
(1.山东省科学院 海洋仪器仪表研究所,山东 青岛 266001;2.山东科技大学 电气与自动化学院,山东 青岛 266590)
倒立摆系统基于能量控制的起摆控制策略研究
高 皜1,曹 琳1,曹茂永2
(1.山东省科学院 海洋仪器仪表研究所,山东 青岛 266001;2.山东科技大学 电气与自动化学院,山东 青岛 266590)
针对直线一级小车倒立摆系统起摆阶段的特点,设计基于能量控制的起摆控制器。通过引入“小车位移极限”、“小车速度极限”和“系统能量保持”的概念,对纯能量控制策略进行了优化。在起摆过程中,既能保证摆杆的快速起稳摆,又能确保小车位移在有限长的范围内。利用MATLAB对系统进行仿真分析,并运用英国Feedback公司生产的倒立摆机械实物系统进行实验验证。结果证明,该控制器能够实现小车倒立摆系统的快速平稳起摆。
倒立摆;能量起摆控制优化; MATLAB仿真;实物验证
倒立摆起摆控制策略研究是非线性系统控制领域的一个经典课题[1]。其中应用最为广泛的启发式继电控制(即Bang-Bang控制)[2-3]策略非常容易实现,但具有敏感度太高的缺点[4]。Åström等提出了一种全新的基于能量控制的起摆策略,可以被应用于无限长直轨道的情况,但只能局限在理论研究层面,并不适用于倒立摆系统的实时控制[5-10]。本文在纯能量控制策略的基础上,对小车倒立摆系统的起摆控制策略进行改进和优化,通过引入“小车位移极限”、“小车速度极限”和“系统能量保持”等概念,使其不仅能满足系统对摆杆角度的要求,还能满足对小车位移的限制,为后续的实物系统试验和应用提供了新的途径。
1 直线一级小车倒立摆系统建模
直线一级小车倒立摆作为一个欠驱动机械系统,拥有两个自由度和一个系统输入[5,8],如图1所示。在

图1 小车倒立摆系统结构图Fig.1 Inverted pendulum mechanical system
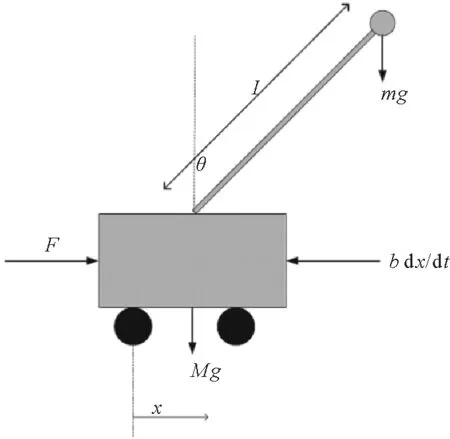
图2 直线一级小车倒立摆系统数学模型示意图Fig.2 Mathematical model of cart-pendulum system
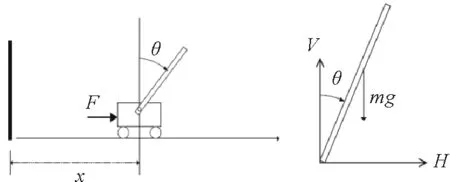
图3 一级直线小车倒立摆系统输入/输出及受力分析图Fig.3 Input/outputs and force analysis of cart-pendulum system
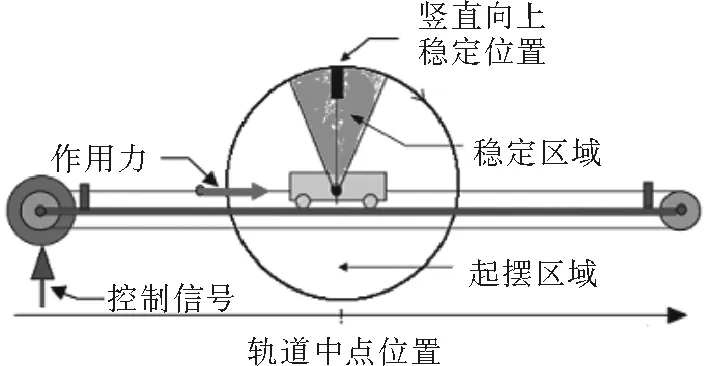
图4 小车倒立摆系统起摆/稳摆过程示意图Fig. 4 Swing-up/stabilization controller zone of the inverted pendulum
无外力施加的状态下,该倒立摆系统有向最低点摆动的趋势,最低点位置是稳定的,被称作倒吊位置,与之相反的最高点为不稳定的直立位置[6-9]。
对该系统建模之前,作如下假设:小车可视为质点;引入参数d,表征空气阻力及摩擦带来的阻尼衰减系数;摆杆为刚性轻质杆;驱动系统的传动带不可伸缩。如图2所示,小车质量M,倒立摆质量为m,摆杆长度为l(即倒立摆质心距转轴的距离),小车水平位移为x,θ为摆杆偏离竖直向上方向沿顺时针转动的夹角(逆时针方向为负值),重力加速度为g,b是小车粘滞摩擦系数。另外,将施加在小车上的力F作为系统输入,将小车位移x和摆杆角度θ作为系统输出。
依据上述分析,对该系统进行受力分析,如图3所示。
在水平和竖直方向对倒立摆应用牛顿运动定律,有
(1)
其中:H为水平分量,V为竖直分量。
在水平方向对小车应用牛顿运动定律,有
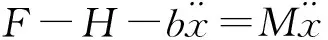
(2)
考虑到摆杆质心的转动惯量I,有
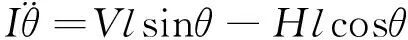
(3)
综上所述,得到该直线一级小车倒立摆系统的的非线性动力学描述:

(4)
2 起摆控制策略研究
直线一级小车倒立摆系统的起摆控制问题可以描述为:通过外力驱动小车,在有限长的水平直轨道上往复运动,将与之相连可以自由转动的摆杆从竖直向下的稳定位置,摆至竖直向上的不稳定平衡位置。整个起摆过程,要求快速平稳,既要尽可能缩短起摆时间,又要尽可能减小进入稳定区域的摆杆角速度,保证下一阶段稳摆控制规律的平滑切换,如图4所示。
2.1 经典起摆控制策略缺陷
基于运动逻辑的Bang-Bang起摆控制器是在小车上施加一个恒定大小的作用力,根据摆杆的起摆运动情况,改变施力的方向,驱动小车在轨道上来回运动,直到将摆杆摆到竖直向上位置,完成起摆动作[4]。这种控制策略十分直接有效,但在实际应用中,由于轨道长度的限制,该作用力参数的整定十分困难。如果该值太大,小车将会冲出轨道或者摆杆在摆到竖直向上位置的角速度太大,无法完成稳摆;如果该值太小,系统将不能得到足够的能量,无法将摆杆摆到最高位置[6]。只有在仿真控制和实物实时控制时,对驱动力的幅值进行正确的整定,才能确保该逻辑控制器能够逐步向倒立摆系统注入能量直到摆杆摆至竖直向上的位置。另外,该控制策略必须与另一个控制小车位移的PI控制器联合作用,才有可能在完成起摆动作的同时,保证小车的位移在有限长的范围内。
由Astrom 和 Furuta 提出的纯能量控制策略[7],核心思想是以对摆杆的能量控制取代对小车位移的控制,来完成起摆过程。具体来说,就是在小车上施加特定的力,为整个系统注入能量,使整个系统的机械能逐步增加,一旦达到了竖直向上位置所应具有的能量值,就意味着摆杆已经摆到了最高点,起摆过程实现。显然,这种纯能量控制策略,能够实现起摆任务,但是只有在小车轨道长度无限或者闭合圆轨道(模拟无限长直轨道)的情况下才有效果。然而,在实际生产生活中,施加的外力大小和小车的轨道长度都必然是有限的。这就给该能量控制策略的实际应用带来了极大的障碍。
2.2 基于能量控制的起摆控制器优化
本文基于纯能量控制策略,引入“小车位移极限”、“小车速度极限”和“系统能量保持”等概念,对小车倒立摆系统的起摆控制策略进行改进和优化,使其不仅能满足系统对摆杆角度的要求,还能满足对小车位移的限制。
改进型的起摆能量控制策略由四部分组成:一是以纯能量控制策略为基础的Bang-Bang控制;二是小车位移极限(势阱);三是小车速度极限(势阱);四是系统能量保持,如图5所示。

图5 改进型整合起摆能量控制策略示意图Fig.5 Modified energy swing-up controller
改进的能量控制策略能够实现系统的综合控制,不仅能限制小车位移在有限范围内,而且整个起摆的动态过程可以调节。可通过整定系统的四个参数Ksu、Kcw、Kvw和Kem,调节摆杆从起摆开始直到摆到竖直向上位置所需要的摆动次数,提高控制系统的系统适应性和容错率。
1) 改进的纯能量控制策略
纯能量控制策略的一大缺点是在系统机械能逐步增大到竖直向上位置应具有的能量值过程中,能量的增速会逐渐放缓,导致起摆时间较长。为克服这个缺陷,将纯能量控制策略做如下改进:

(5)
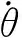
2) 小车位移极限(ucart-well)
为了克服纯能量控制策略只有在轨道长度无限的情况下才能有效的缺点,引入一个小车位移极限(势阱)的概念。为此,定义一个小车位移极限方程,将小车的位移限制在有限长的轨道上。
根据倒立摆的摆动特性,小车位移控制规律可以描述为:

(6)
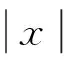
3) 小车速度极限(uvelocity-well)
引入小车速度极限的概念,通过始终保证控制系统回路为负反馈来满足小车在摆杆摆动到竖直向上不稳定平衡位置时的速度要求。小车速度极限的控制规律可描述为:

(7)
4) 系统能量保持(uenergy-maintain)
为了保证起摆和稳摆两种控制规律的顺利切换,引入“系统能量保持”控制规律[10]。该控制规律能够克服摩擦损失,保持系统机械能直到稳摆控制器产生作用效果。具体描述为:
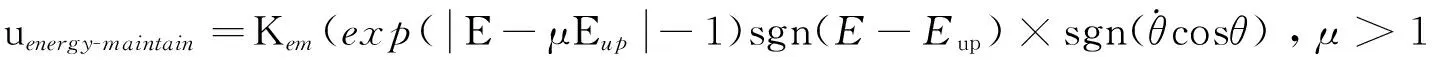
(8)
其中:E表示系统机械能;Eup表征竖直向上不稳定平衡位置所应具有的能量值,通过整定参数能够保证起摆和稳摆两种控制规律的平稳过渡。
四种控制策略的联合作用,能够实现更加快速平稳的起摆过程,控制效果比纯能量控制要更好,而且由于限制了小车位移,使得在实验平台上验证控制效果成为可能。
与以往的倒立摆起摆控制策略相比,改进型的能量起摆控制器具有如下显著优点:①在起摆模式下,系统能量注入能被精确控制,该小车速率在整个起摆过程中基本保持线性,加快了系统的瞬态响应速度;②该控制策略有明确直观的解释,其稳定的充分条件也合乎逻辑。验证表明,当设定的限制条件被“突破”时,将会导致系统的不稳定;③该控制系统可以被视作一个由多个运行模式组成的混合控制器,有利于进一步实现模块化设计,将该控制器设计思路推广到多级倒立摆系统中;④该控制策略能够精确控制小车的运动状态以及摆杆的转动状态。
3 小车倒立摆控制系统仿真实验和实物验证
依据直线一级小车倒立摆系统的非线性模型,运用MATLAB中Real-TimeSimulation对起摆及稳摆控制器进行仿真,探讨改进型基于能量控制的起摆控制器的控制效果。该控制系统由四大部分组成:小车倒立摆系统的非线性模型;基于能量控制的改进型起摆控制器;基于LQR设计的稳摆控制器;逻辑开关,用于在起摆和稳摆两种控制规律间的切换。小车倒立摆实物实时控制系统,是由英国FEEDBACK公司生产的Ⅱ型设备,集成了传感器、数模/模数转换器和控制单元。
通过整定起摆控制器的四组参数,使摆杆分别经历3次、4次和6次摆动,完成起摆动作。仿真实验和实物机械系统验证结果如图6~8所示。
1) 经历3次摆动完成起摆的情况
起摆控制器参数选取为:Ksu=0.65、Kcw=0.22、Kvw=0.8、Kem=0.01。
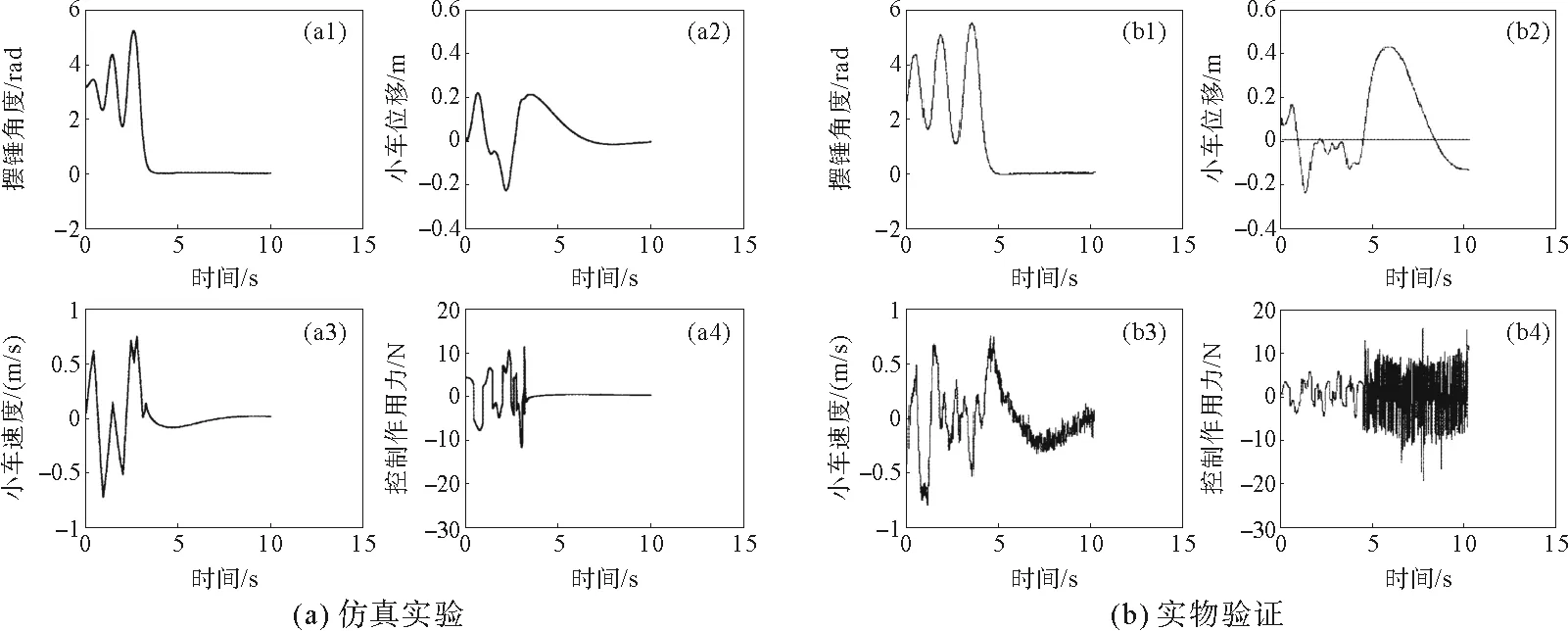
图6 经历3次摆动起摆的情况,仿真实验和实物验证结果Fig.6 Simulation and implementation results for three swings
2) 经历4次摆动完成起摆的情况
起摆控制器参数选取为:Ksu=0.56、Kcw=0.22、Kvw=0.8、Kem=0.01。

图7 经历4次摆动起摆的情况,仿真实验和实物验证结果Fig.7 Simulation and implementation results for four swings
3)经历6次摆动完成起摆的情况
起摆控制器参数选取为:Ksu=0.48、Kcw=0.22、Kvw=0.8、Kem=0.01。
图6~8中,图(a)为利用MATLAB仿真的实验结果,图(b)为小车倒立摆实物系统验证结果。可以看出,实物系统起摆实验的结果与仿真验证的结果保持较高的一致性。然而,由于实物系统结果中含有系统噪声,因而需要更长的时间来到达稳定状态。噪声主要是在对速度环节的处理过程中产生。另外在系统建模和控制器设计过程中,并没有将全部摩擦阻力纳入考虑范畴。三种情况下,理论仿真和实验验证均取得了一致的结果,证明了本文提出的基于能量控制的改进型起摆控制器不仅能够实现起摆控制目标,而且可对小车的位移和摆杆的姿态进行精确控制。
图8 经历6次摆动起摆的情况,仿真实验和实物验证结果Fig.8 Simulation and implementation results for six swings
4 结 论
针对纯能量控制策略的不足,通过对小车倒立摆系统起摆控制策略研究,设计了一种改进型能量控制策略。引入“小车位移极限”、“小车速度极限”和“系统能量保持”的概念,解决了摆杆快速起摆的问题,能满足系统对于小车位移的限制。通过实物验证,该改进型控制策略能够有效地对小车倒立摆系统的起摆过程进行控制,通过对控制器参数的整定,不仅可以将小车位移控制在有限的距离内,而且能够对整个起摆过程(包括起摆耗时、摆动次数、摆动趋向等)进行精确控制。
[1]李雪冰, 马莉, 丁世宏,等. 一类新的二阶滑模控制方法及其在倒立摆控制中的应用[J]. 自动化学报, 2015,41(1):193-202. LI Xuebing,MA Li,DING Shihong,et al. A new second-order sliding mode control and its application to inverted pendulum[J]. Acta Automatica Sinica, 2015,41(1):193-202.
[2]宋清昆, 李东威. 二级倒立摆控制器设计及稳定性研究[J]. 计算机仿真, 2015, 32(4):305-309. SONG Qingkun,LI Dongwei. The design and stability study of double inverted pendulum controller[J]. Computer Simulation, 2015, 32(4):305-309.
[3]蔺小林, 邓雄峰, 李露. 基于参数自适应模糊PI的三级倒立摆控制[J]. 控制工程, 2015, 22(3):404-408. LIN Xiaolin, DENG Xiongfeng, LI Lu. Control for triple inverted pendulum based on parameter adaptive fuzzy PI[J]. Control Engineering of China, 2015, 22(3):404-408.
[4]刘继光, 王丽军, 袁浩. 自立倒立摆系统的自摆起及稳定控制[J]. 实验技术与管理, 2015,32(11):62-65. LIU Jiguang,WANG Lijun,YUAN Hao. Self-swinging up and stable control of self-erecting inverted pendulum system[J].Experimental Technology and Management, 2015,32(11):62-65.
[5]钱苇航, 闻新. 基于MATLAB的倒立摆特征根灵敏度分析[J]. 价值工程, 2016, 35(9):206-208. QIAN Weihang;WEN Xin. Sensitivity analysis of inverted pendulum characteristic root based on MATLAB[J]. Value Engineering, 2016, 35(9):206-208.
[6]高强, 陈莎莎, 李毅. 线性自抗扰控制在倒立摆系统的实现[J]. 电气传动, 2014, 44(10):49-53. GAO Qiang,CHEN Shasha, LI Yi. Application of LADRC on inverted pendulum system[J].Electric Drive, 2014, 44(10):49-53.
[7]ÅSTRÖM K J. Furuta. Swinging up a pendulum by energy control[J]. Automatica, 2000, 36, 287-295.
[8]张霖, 李俊民. 车载倒立摆系统非线性未建模动态的CMAC补偿控制[J]. 控制工程, 2014(增1):121-124. ZHANG Lin,LI Junmin. CMAC compensating control for vehicle - mounted inverted pendulum system with nonlinear unmodeled dynamics[J]. Control Engineering of China, 2014(S1):121-124.
[9]刘慧博, 蔡蕊. 直线二级倒立摆基于线性矩阵不等式算法的滑模鲁棒H∞控制[J]. 科学技术与工程, 2014, 14(5):270-275. LIU Huibo,CAI Rui.Sliding mode and robustH∞control based on LMI algorithm for linear double inverted pendulum[J].Science Technology and Engineering,2014,14(5):270-275.
[10]BRADSHAW A, SHAO J. Swing-up control of inverted pendulum systems[J]. Robotica, 1996,14:397-405.
(责任编辑:傅 游)
Swing-up Control Strategy Analysis of Inverted Pendulum Based on Energy Control
GAO Hao1, CAO Lin1, CAO Maoyong2
(1. Institute of Oceanographic Instrumentation, Shandong Academy of Sciences, Qingdao, Shandong 266001, China;2. College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao, Shandong 266590, China)
Based on the swing-up characteristics of the linear single inverted pendulum, a swing-up controller based on energy control was designed. By introducing the concepts of “Cart Potential Well”, “Velocity Well” and “Energy Maintenance”, the pure energy-based control strategy was optimized. The design not only ensured the quick and smooth swing-up of the pendulum rod but also the displacement of the cart within a limited length during the whole swing-up period. Then the pendulum system was simulated by using MTALAB and real-time experiments were made by using the inverted pendulum manufactured by the British Feedback company. The experimental results indicate that the proposed controller is able to achieve the quick and smooth swing-up of the inverted pendulum.
inverted pendulum; modified energy-based swing-up controller; MATLAB simulation; real-time application
2015-11-08
“十二五”国家科技支撑计划项目(2012BAB13B04)
高 皜(1988—),男,山东汶上人,硕士,主要从事自动控制研究与应用. 曹 琳(1988—),女,山东青州人,硕士,主要从事自动化及监测监控技术研究,本文通信作者. E-mail: 759925933@qq.com
TP13
A
1672-3767(2016)06-0095-06
