一种改进的全局和声搜索算法求解函数优化问题

周园园，胡贤德，李敬明，沈桂芳

（安徽新华学院 信息工程学院，安徽 合肥 230088）

一种改进的全局和声搜索算法求解函数优化问题

周园园，胡贤德，李敬明，沈桂芳

（安徽新华学院 信息工程学院，安徽 合肥 230088）

针对和声搜索算法的早期收敛速度快，后期收敛慢，容易陷入局部最优解的问题，本文提出了一种改进的全局和声搜索算法.该算法对标准和声搜索算法作了三点改进，首先在和声记忆库初始化时采用反向学习策略，提高初始解的质量，提高收敛速度，其次，采用动态方式调整参数，第三，利用当前和声记忆库中的全局最优解产生新解，提高全局搜索能力.采用该算法对6个标准的测试函数进行优化，结果表明，该算法避免算法的早熟和增强算法的全局搜索能力，具有较好的优化性能.

和声搜索算法；反向学习；函数优化

1 引言

和声搜索算法（Harmony Search，简称HS）是一种较新的智能搜索算法[1].该算法结构简单，易于其他算法结合，已经成功地被应用到函数优化问题中.相关研究表明，在解决多维函数优化问题上HS算法比较遗传算法、模拟退火算法等具有更好的优化性能[2-5].但该算法在迭代早期具有较快的收敛速度，后期收敛速度较慢，算法的收敛速度很大程度依赖于初始解.反向学习策略已经被证明能产生高质量的初始解[6]，提高算法的收敛速度，而且已经被成功地应用到其他的智能算法的解空间的初始化中.为了提高和声记忆库中解的质量，避免算法陷入局部最优解，本文将反向学习方法、粒子群中全局最优解的概念与和声搜索算法结合起来，提出一种改进的和声搜索算法——反向学习全局和声搜索算法.

2 和声搜算法

HS算法模拟音乐演奏家创作的过程，音乐家不断地调整所奏乐器的音调，使真个演奏过程达到最美和声状态.HS算法将音乐创作的元素和优化问题中的元量进行类比，将乐器、乐器的音调、和声、和声效果评价与组合优化问题中的决策变量、决策变量的值、决策变量组成的解向量、目标函数的适应度值进行类比.具体的算法步骤如下：

2.1 初始化算法参数

初始化算法参数：①决策变量的个数N，②和声记忆库的大小HMS，③各个决策变量的取值范围[Li,Ui]，④和声记忆库考虑概率HMCR，⑤音调微调概率PAR，⑥音调微调带宽BW，⑦算法的迭代次数NI.

2.2 初始化和声记忆库HM

随机生成HMS个和声x1，x2，……，xHMS存入和声记忆库HM作为优化问题的初始解.

和声记忆库中的每个音调（即决策变量）按照式（1）产生：

其中，i=1,2,……,HMS；j=1,2,……,N；Lj和Uj分别是j分量值域的下界和上界；

2.3 产生一个新的和声

初始化后，HS算法将产生一个新和声x'=(x1',x2',…xN')，新和声中任一音调xi'按照三个规则产生：（1）考虑和声记忆库，（2）随机在值域范围内选择音调，（3）微调来自和声记忆库的音调.具体操作如下：

首先，考虑和声记忆库或者随机产生音调，公式如（2）式：

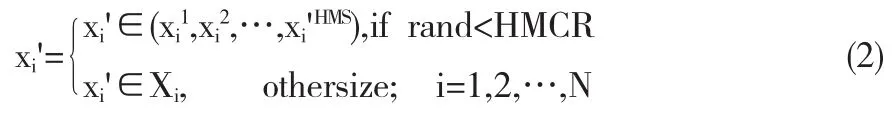
然后，如果新和声中的某个音调xi'来自和声记忆库HM，则有PAR的概率对音调xi'微调，微调的公式如（3）式：

2.4 更新和声记忆库HM

对步骤（3）中的新解进行评估，如果新和声优于HM中的最差的一个和声，则将新解xi'替换HM中当前最差的解.

2.5 检查算法终止条件

重复步骤（3）和步骤（4），直到创作(迭代)次数达到NI为止.

3 改进的全局和声搜索算法

HS算法在解决优化问题上，早期能快速收敛，确定最优解搜索空间，但是会陷入局部最优解，为了解决这个问题，需要利用全局最优解的信息，针对HS算法后期收敛慢的问题，提高收敛速度，采用了反向学习来初始化和声记忆库，提出一种改进的和声搜索算法，叫反向学习全局和声搜索算法（OGHS）.

HS算法的具体改进方面如下：

3.1 和声记忆库初始化

为了提高初始解的质量，本算法采用反向学习的策略产生初始解.不再按照标准的HS算法采用均匀分布的策略，而是采用均匀分布与反向学习相结合的策略对和声记忆库初始化.和声记忆库中一半的解按照均匀分布策略产生如式（1），剩余的一半解采用反向学习策略产生如式（4）和（5）

3.2 BW和PAR参数的动态调整

文献[7]中的测试结果表明，和声搜索算法按照式（6）与（7）比Mahdavi等[8]提出IHS算法中的公式对PAR和BW进行动态调整的寻找的最优解更好，因此，本算法采用式（6）和式（7）对PAR和BW进行动态调整比.

3.3 新解产生方式

为了提高算法的全局搜索能力，避免算法陷入局部最优解，在产生新解的步骤中，保留当前和声记忆库中的最优解，对标准HS算法中的式（3）做了改进，若新解来自于和声记忆库，有一半的概率是来自最优解，新解不再按照式（3）产生，而是按照式（8）产生：

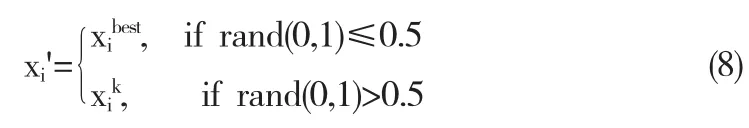
其中，i=1,2,……,n；k=1,2,……,HMS

即将当前和声记忆库中最优解的第j维变量赋值给新解的第j维变量.

3.4 解的边界值处理

当新解超过值域范围，对新解按照式（9）[9]进行处理.

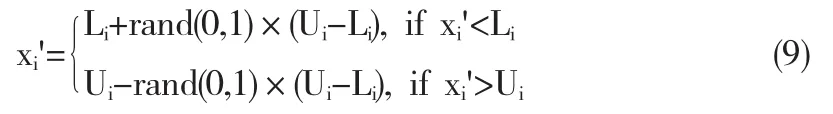
本算法与HS算法的流程整体相同，但对HS算法的初始解的产生和产生新解的核心部分进行了修正.

4 仿真实验及结果分析

为了验证OGHS算法的性能，采用典型的Benchmark测试函数对HS算法、IHS算法、GHS算法、IGHS算法和本文提出的OGHS算法进行测试比较.测试函数如表1所示.函数分别采用30维和100维进行测试.表2是实验中各算法参数设置.

表1 测试函数

表2 不同算法的参数设置

本文中用最优解平均值和标准方差来衡量算法的性能，最优解平均值（MB）的大小能衡量算法的平均搜索能力，标准方差（SD）能说明算法的收敛速度.

表3记录了30维和100维的6个测试函数在各个算法独立运行20次的结果.表中GHS的测试结果来自文献[10].

从表3的测试结果可以看出，在所有的测试函数中IGHS的最优解平均值明显比HS，HIS,GHS的要小，还可以看出GHS在一些单峰函数优化问题上，结果并不优于HS和IHS算法.

5 结论

本文提出一种反向学习全局和声搜索算法（OGHS），该算法首先通过反向学习策略产生和声记忆库初始解，利用动态方式调整PAR和BW参数，然后利用全局信息改变新解产生.仿真实验结果表明，该算法整体上表现出良好的性能，可以用于复杂优化问题的求解.

表3 四种HS算法运算结果比较(运行程序20次)

〔1〕Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001,76(2):60-68.

〔2〕Geem ZW,Lee KS,Park Y.Application of harmony search to vehicle routing.American Journal of Applied Sciences,2005,2(12):1552?1557.

〔3〕Geem ZW.Optimal cost design of water distribution networks using harmony search.Eng Optimiz,2006,38(3): 259-280.

〔4〕Pan Q K,Suganthan P N,Tasgetiren M F,et al.A self-adaptive global best harmony search algorithm for continuous optimization problems[J].Applied Mathematics and Computation,2010,216(3):830-848.

〔5〕Ashrafi,S.M.,&Dariane,A.B.(2013).Performance evaluation of an improved harmony search algorithm for numerical optimization:melody search(MS).Engineering Applications of Artificial Intelligence,26(4),1301–1321.

〔6〕Wang H,Wu Z,Rahnamayan S,et al.Enhancing particle swarm optimization using generalized oppositionbased learning [J].Information Sciences,2011,181(20): 4699-4714.

〔7〕韩红燕,潘全科,梁静.改进的和声搜索算法在函数优化中的应用[J].计算机工程,2010,36(13):245-247.

〔8〕Mahdavi M,Fesanghary M,Damangir E.An improved harmony search algorithm for solving optimization problems[J].Applied mathematics and computation,2007,188 (2):1567-1579.

〔9〕Gong,W.,Cai,Z.,&Ling,C.X.(2010).DE/BBO:a hybrid differential evolution withbiogeography-based optimization for global numerical optimization.SoftComputing,15(4),645–665.

〔10〕Omran M G H,Mahdavi M.Global-best harmony search [J].Applied Mathematics and Computation, 2008,198(2):643-656.

TP393

A

1673-260X（2016）11-0015-03

2016-06-22

安徽省教育厅自然科学基金重点项目（KJ2016A308)