快速校正天波雷达电离层相位污染的改进方法*

张立东,李居尚

(长春理工大学光电信息学院,长春130012)

快速校正天波雷达电离层相位污染的改进方法*

张立东**,李居尚

(长春理工大学光电信息学院,长春130012)

时变的电离层会对天波超视距雷达(OTHR)回波信号相位进行调制,产生相位污染,导致回波谱展宽。最大似然估计(MLE)法具有比相位梯度法更佳的污染校正效果,但计算量非常大。通过引入投影近似子空间跟踪法,提出了一种改进的MLE方法。改进方法采用递归手段估计最大特征值对应的特征向量,避免了特征值分解过程,能够显著降低计算量,污染校正效果与MLE法相当。理论分析与仿真对比表明改进方法普适性强,计算量只有MLE法的万分之一,更适合工程实现。

天波超视距雷达;电离层相位污染校正;最大似然估计;投影近似子空间跟踪

现有的非线性相位污染校正方法主要分为3类:第一类是对长相干积累时间(Coherent Integration Time,CIT)下的回波数据进行分段,将每段短时间序列内的相位污染视为线性的,由每段短回波序列的瞬时频率积分得到全部相位污染,如特征分解法[3]和三次相位建模法[4-5];第二类是由相邻回波的相位差估计相位污染,如相位梯度自聚焦(Phase Gradient Autofocus,PGA)法[6-7]、协方差矩阵求解法[8]和能量检测器法[9];第三类是将相位污染用多项式相位信号来逼近,如多项式相位建模法[10]。文献[11]提出采用最大似然估计(Maximum Likelihood Estimation,MLE)法对OTHR回波相位污染进行校正,能够取得优于PGA法的校正效果,但该方法需要对回波协方差矩阵进行特征分解,长相干积累时间下的回波序列较长,其协方差矩阵维数较大,导致特征值分解的计算量剧增,严重降低了MLE法的运算效率。针对该情况,本文引入投影近似子空间跟踪法[12-13],提出了一种校正非线性相位污染的改进MLE法。该方法不需要进行特征值分解,在保证MLE法估计精度的前提下,大大减小了方法的运算量。

2 OTHR回波相位污染模型

OTHR目前主要采用的是线性调频连续波信号,其回波信号可以写成如下形式:

式中:c(n)为地、海杂波;s(n)为飞机和舰船等运动目标;i(n)为瞬态干扰、无源干扰等;ξ(n)为噪声, n=1,2,…,N为相干积累脉冲数。不考虑干扰, OTHR回波中只含有地、海杂波和运动目标,则式(1)可写为

式中:fB=0.102fc为一阶海杂波频率[7](fc为OTHR发射频率,单位为MHz);k=±1分别对应于正负一阶海杂波(一阶Bragg峰);cl分别为正负一阶Bragg峰幅度;sp和fp分别为第p个目标信号的幅度和多普勒频率。

当电离层非稳定变化时,将对OTHR回波信号相位进行非线性调制,遭受到电离层相位污染后的回波信号表示为

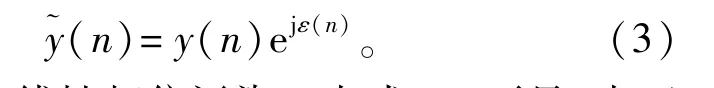
式中:ε(n)为非线性相位污染。由式(3)可见,由于ε(n)是非线性变化的,当它对OTHR回波信号y(n)的相位进行调制时,y(n)信号原本线性变化的相位,将会呈现出非线性变化,其瞬时频率不再恒定,也将会出现非线性变化,所以受到相位污染后的回波~y(t)的谱线会发生展宽。在相位污染严重的情况下~y(t)谱线甚至会产生分裂,无法准确检测出慢速目标,进行污染校正的目的就是去除回波中的相位污染成分,从直观上看就是使得频谱得到锐化,目标和地、海杂波能够区分,提高OTHR的目标检测性能。

3 MLE校正方法

受到电离层污染的OTHR回波谱虽然发生了展宽,但其正负Bragg展宽峰一般是可分的,现有的方法[3-11]均是基于提取出的单个展宽Bragg峰进行相位污染估计的。假设正的Bragg展宽峰较负的Bragg展宽峰能量占优,采用带通滤波器将正的Bragg展宽峰提取出来作为标校信号,则提取出的标校信号可以表示为

式中:n=1,2,…,N为相干积累脉冲数。将时域的标校信号~y+(n)变换到频域,并将峰值(即正一阶Bragg峰值谱线)移至0 Hz,此时式(4)中的fB变为了0 Hz,则式(4)中仅包含相位污染ε(n)和噪声ξ(n),即~y+(n)=c1ejε(n)+ξ(n),由于ε(n)非线性变化,则~y+(n)的相位也会呈现非线性变化,在频域表现为谱线展宽。可将式(4)写为向量形式:

式中:~ym+为第m个距离单元移频后的标校信号, ~ym+=[~ym+(1),~ym+(2),…,~ym+(N)]T,m=1,2,…,M; v=[ejε1,ejε2,…,ejεN]T;ξ为噪声向量。

假设ξ是高斯白噪声,均值为0,方差为σ2,由于幅度c1是常量,则~ym+服从高斯分布,~ym+的概率密度函数写为[11]

式中:μ~ym+=c1v为~ym+的均值;C~ym+=σ2I。将相邻M个回波距离单元的信号组成矩阵~y+=[~y1+,~y2+,…, ~yM+],~y+的概率密度函数为[11]M

式中:p(y~+|v)是估计量v的似然函数,当v^被准确估计时,式(7)达到最大值。对矩阵m∑M=1y~m+y~Hm+进行特征值分解,解出最大特征值对应的特征向量即获得了污染向量的估计值[11]。

4 改进的MLE校正方法

虽然MLE法在估计相位污染时能够取得较精确的估计结果,但是OTHR回波脉冲数越大,对回波协方差矩阵进行特征值分解时的运算负担也越大,尤其在处理OTHR对海探测回波数据时,该方法的运算效率较低。因为OTHR处于对海探测模式时,为了有效积累舰船等慢速目标能量,需要较长的CIT,一般CIT要大于20 s,这种模式下的相干积累脉冲数目很大,所以特征值分解需要耗费大量的时间,降低了MLE法的处理效率。投影近似子空间跟踪(Projection Approximation Subspace Tracking, PAST)法[12-13]能够避免MLE法中对回波协方差矩阵进行估计和特征值分解两步过程,利用递归方法对子空间进行估计,用其估计相位污染,可以大大提高MLE法的实时性。

假设λ和u分别是矩阵∑Mm=10m+~yHm+的最大特征值和特征向量,λ(i)和ui是第i次迭代估计得到的特征值和特征向量,i=1,2,…,M,M为参与相位污染估计的回波信号距离单元数,第i次估计的特征向量ui用下式进行迭代计算:

式中:*表示取共轭运算;Δi和w(i)为中间运算变量。Δi、w(i)和λ(i)分别由下列公式进行迭代计算:

将式(9)～(11)代入式(8),可得

假设特征值和特征向量的初始值分别为λ(0)=0和u0=[1,1,…,1]T,则式(12)可写为

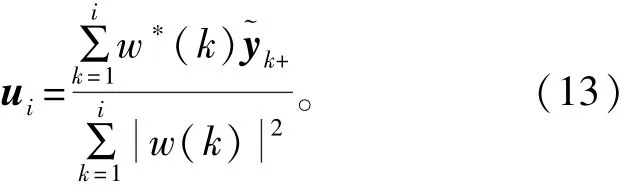
由式(13)可以看出,ui完全可以由参与计算的多个距离单元回波脉冲信号直接计算出来,避免了MLE法中对协方差矩阵的估计以及进行特征值分解。同时,若将w(i)视为权值,则式(13)也可以看成是利用权值对各距离单元信号进行加权累加后求其平均值,根据MLE法的推导,该ui即为估计出的电离层相位污染。

综上所述,改进MLE法的流程可以总结如下:

(1)采用带通滤波器,提取出各距离单元的标校信号~ym+(假设正的Bragg峰能量占优);

(2)根据PAST法,利用式(13)估计电离层相位污染ui;

(3)利用ui对受到电离层调制的回波信号~y进行补偿校正,消除相位污染。

5 方法性能与仿真结果分析

5.1 污染校正结果分析

在本节中,将通过实验仿真来检验第4节提出的改进MLE法校正电离层相位污染的有效性,同时对文献[11]提出的MLE法和文献[7]提出的IPGA法进行仿真,比较各种方法的污染校正结果。参考文献[4],将实验中的仿真参数设定为:OTHR发射电磁波的频率为15 MHz,雷达脉冲重复频率为10 Hz,其对应的脉冲数为512个,可计算出CIT为51.2 s,参与估计的距离单元数为 20个。两个Bragg峰分量的幅度分别为6和4,杂噪比为15 dB,舰船目标的多普勒频率为-0.3 Hz,信噪比为4 dB。参考国内外学者的做法,在仿真中将正弦型函数作为非线性相位污染[4-11],对天波雷达回波添加的相位污染为1.2sin(2π·0.01t),1.2为相位污染的幅度,代表污染能量的大小;0.01 Hz为扰动频率,代表污染变化的快慢。

图1(a)是未遭受电离层相位污染的某个回波距离单元的频谱图,图1(b)是人为添加非线性相位污染后的频谱图。从图1可以看出,工作频率为15 MHz的 OTHR 中的一阶 Bragg峰频率为±0.395 Hz,污染前的谱线清晰锐利,舰船目标的多普勒频率为-0.3 Hz;受到电离层污染后两个海杂波峰变宽,并且负的海杂波展宽峰掩盖了其附近的舰船目标,导致OTHR无法检测出舰船目标。

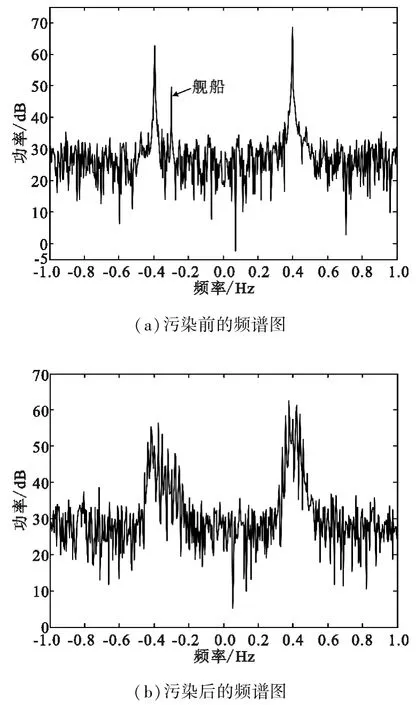
图1　OTHR回波电离层相位污染前后的频谱图Fig.1 The echo spectrum of OTHR before and after ionospheric phase contamination

分别采用MLE法、IPGA法以及本文提出的改进MLE法对图1(b)中的电离层污染进行校正,结果如图2所示。图2(a)是3种方法估计出的相位污染。其中实线函数是实际添加的相位污染。由图可见,3种方法能够较准确地估计出污染,但从估计误差大小的角度看,MLE法和改进MLE法的估计误差基本相当,略小于IPGA法的估计误差。图2 (b)～(d)是经过3种方法校正污染后的回波频谱图,可以看出,3种方法均能够较好地去除电离层污染,受到污染的展宽频谱得到了很好锐化,但MLE法和改进 MLE法对谱线的恢复程度要略优于IPGA法。

图2　3种方法校正电离层污染后的结果Fig.2 The result after ionospheric phase contamination correction by three approaches

5.2 普适性分析

为了验证改进MLE法的普适性,对回波信号添加不同类型的非线性相位污染,考察该方法的校正效果,同时与MLE法和IPGA法的污染估计结果进行比较。实验仿真参数与5.1节一致,只是人为添加的非线性污染形式不同,分别添加下列两种污染: 0.05e0.008t·sin(2π·0.01t)和cos(2π·0.013t)· sin(2π·0.01t),将它们称为非线性相位污染1和污染2,污染估计结果如图3所示。从图3可以看出,改变污染的形式后,3种方法同样能够较准确地估计出相位污染,但是不管是添加污染1还是污染2,改进MLE法和MLE法的估计效果均要略优于IPGA法,说明两种方法的估计精度更高,同时也说明改进MLE法采用投影近似子空间跟踪技术估计最大特征值对应的特征向量与MLE法中对协方差矩阵进行特征值分解得到的特征向量是非常吻合的。

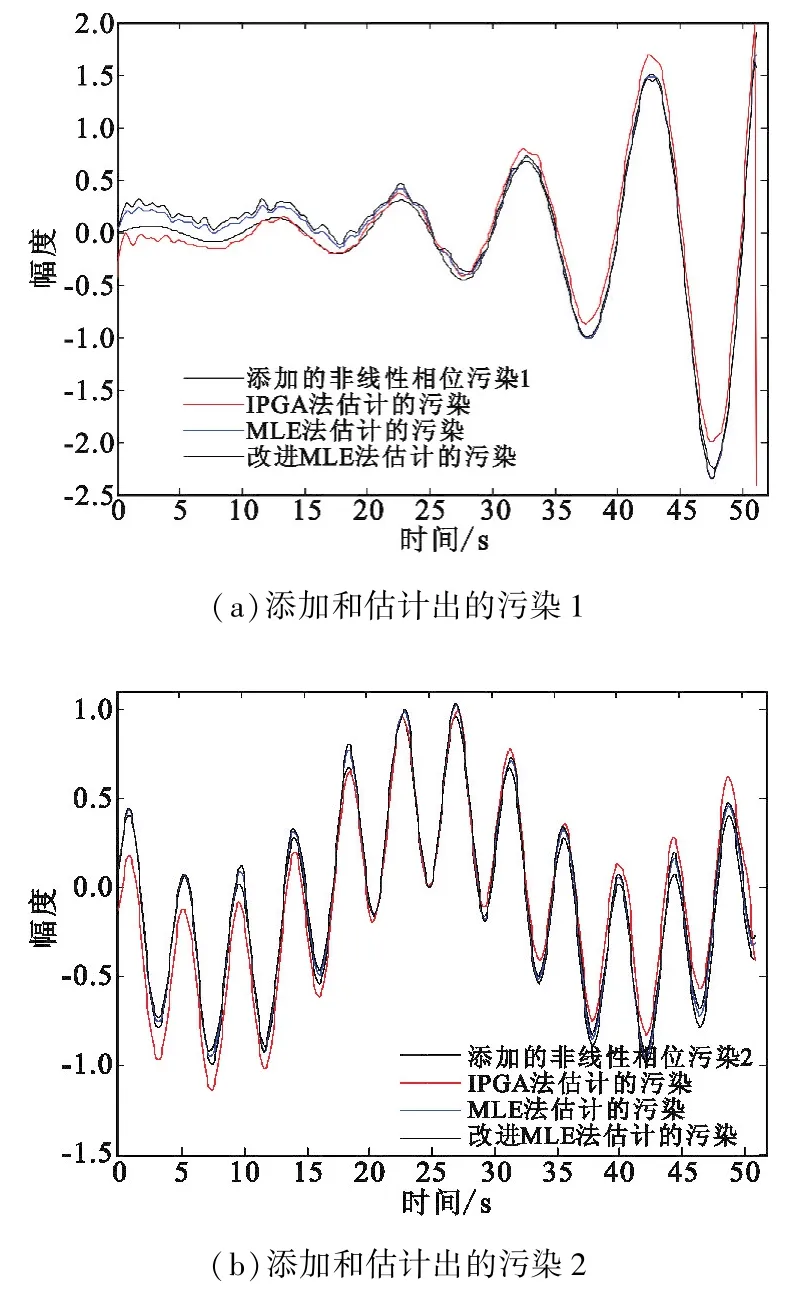
图3　3种方法估计电离层污染1和污染2后的结果Fig.3 The estimation of ionospheric contamination 1 and contamination 2 by three correction approaches

5.3 运算量分析

从5.1节和5.2节的仿真对比可以看出,改进MLE法和MLE法的污染估计性能基本相当,略好于IPGA法。下面分析3种方法的运算量。

MLE法的计算量主要在对协方差矩阵的特征值分解上,参与估计的回波脉冲数为N,协方差矩阵即是一个N×N的矩阵,若忽略估计协方差矩阵的计算量,MLE法的运算复杂度为O(N3);改进MLE法的计算量主要在迭代估计最大特征值对应的特征向量上,该方法不需要估计协方差矩阵,其运算复杂度为O(N)。为定量比较3种方法的计算量,计算3种方法在运算过程中需要的复数乘法次数。假设参与估计的回波距离单元数为M,MLE法中估计协方差矩阵需要MN2次复数乘法运算,对协方差矩阵进行特征值分解需要3N3次复数乘法运算,所以MLE法的总的计算量为MN2+3N3;改进MLE法利用式(13)迭代估计特征向量,每次迭代的计算量为3N次复数乘法运算,总共需要迭代M次(M个距离单元),所以改进MLE法的总的计算量为3MN;IPGA法中,对每个回波距离单元取相位梯度需要N-1次复数乘法,M个距离单元共需要M(N-1)次复数乘法,最小二乘准则修正估计污染的斜率需要3N次复数乘法,所以IPGA法总的计算量为M(N-1)+ 3N。一般地,参与估计的距离单元数M均大于3,甚至是3的数倍,所以3种方法的计算量大小为MLE＞改进MLE≈IPGA。

为了更直观地比较3种方法计算量,假设N= 512,M=5,MLE的计算量是改进MLE的52 599倍,改进MLE的计算量是IPGA的1.88倍。可以看出,改进MLE法的计算量与IPGA法基本相当,但远远小于MLE法。改进MLE法在保证电离层污染估计精度的情况下,显著地减小了计算量,增强了方法的实时处理能力。

6 结束语

本文针对MLE法在校正天波雷达电离层相位污染时计算量过大的问题,引入PAST技术,提出了改进的MLE法。改进方法不需要估计协方差矩阵,采用PAST技术估计最大特征值对应的特征向量,避免了MLE法中特征值分解带来的计算负担过大的问题。实验对比仿真和方法性能分析表明,改进MLE法对电离层污染的校正能力与MLE法基本相当,略优于IPGA法,但是方法的计算量大大降低,明显提高了方法的运算效率,减轻了OTHR信号处理系统的硬件负担。本文方法与目前国内外学者所提方法[3-11]都需要获得纯净度较高的标校信号,但是在高等级海态和电离层变化非常剧烈的情况下,提取完整且纯净的标校信号十分困难,所以实现电离层相位污染的盲校正是一个很有价值的研究方向。

[1] 周万幸.天波超视距雷达发展综述[J].电子学报, 2011,39(6):1373-1378. ZHOU Wanxing.An overview on development of skywave over-the-horizon radar[J].Acta Electronica Sinica, 2011,39(6):1373-1378.(in Chinese)

[2] SHEPHERD R A,LOMAX J B.Frequency spread in ionospheric radio propagation[J].IEEE Transactions on Communication Technology,1967,COM-15(2):268-275.

[3] ANDERSON S J,ABRAMOVICH Y L.A unified approach to detection,classification and correction of ionospheric distortion in HF sky wave radar systems[J].Radio Science,1998,33(3):1055-1067.

[4] 游伟,何子述,陈绪元,等.基于三次相位建模的天波雷达污染校正[J].电波科学学报,2012,27(5):875-880. YOU Wei,HE Zishu,CHEN Xuyuan,et al.Skywave radar decontamination based on the cubic phase model[J].Chinese Journal of Radio Science,2012,27(5):875-880. (in Chinese)

[5] 胡进峰,艾慧,李万阁,等.基于匹配傅里叶变换的相位解污染算法[J].雷达科学与技术,2015,13(3):291-295. HU Jinfeng,AI Hui,LI Wange,et al.An algorithm based on the matched Fourier transform to compensate phase contamination[J].Radar Science and Technology,2015, 13(3):291-295.(in Chinese)

[6] 邢孟道,保铮.电离层电波传播相位污染校正[J].电波科学学报,2002,17(2):129-133. XING Mengdao,BAO Zheng.Phase perturbation correction in ionospheric electromagnetic wave propagation[J]. Chinese Journal of Radio Science,2002,17(2):129-133.(in Chinese)

[7] 罗欢,陈建文,鲍拯.一种天波超视距雷达电离层相位污染联合校正方法[J].电子与信息学报,2013,35 (12):2829-2835. LUO Huan,CHEN Jianwen,BAO Zheng.A joint method to correct ionospheric phase perturbation in over-the-horizon radar[J].Journal of Electronics&Information Technology,2013,35(12):2829-2835.(in Chinese)

[8] LUO H,CHEN J W,BAO Z.A novel method to eliminate ionospheric phase contamination in OTHR systems[C]// Proceedings of the 10th International Symposium on Antennas,Propagation and EM Theory.Xi′an:IEEE,2012: 423-427.

[9] WEI Y,HE Z S,WANG S L.Ionospheric decontamination for skywave OTH radar based on complex energy detector[J].EURASIP Journal on Advances in Signal Processing,2012(1):1-8.

[10] LU K,LIU X Z,LIU Y T.Ionospheric decontamination and sea clutter suppression for HF skywave radars[J].IEEE Journal of Oceanic Engineering,2005,30(2):455-462.

[11] 罗欢,陈建文,鲍拯.同时校正电离层幅度和相位污染的MLE方法[J].华中科技大学学报(自然科学版),2013,41(9):17-21. LUO Huan,CHEN Jianwen,BAO Zheng.Maximum likelihood estimation of correcting ionospheric amplitude and phase contamination simultaneously[J].Journal of Huazhong University of Science&Technology(Natural Science Edition),2013,41(9):17-21.(in Chinese)

[12] YANG B.Projection approximation subspace tracking [J].IEEE Transactions on Signal Processing,1995,43 (1):95-107.

[13] SHEN M W,ZHU D Y,ZHU Z D.Reduced-rank space -time adaptive processing using a modified projection approximation subspace tracking deflation approach[J]. IET Radar,Sonar and Navigation,2009,3(1):93-100.

张立东(1978—),男,吉林长岭人,2002年获学士学位,现为长春理工大学光电信息学院讲师,主要研究方向为信号识别与处理;

ZHANG Lidong was born in Changling,Jilin Province,in 1978.He received the B.S.degree in 2002.He is now a lecturer.His research concerns signal indentification and processing.

Email:ztg_1596@sina.com

李居尚(1984—),女,吉林长春人,2007年获学士学位,现为长春理工大学光电信息学院讲师,主要研究方向为电子技术、信号处理。

LI Jushang was born in Changchun,Jilin Province,in 1984. She received the B.S.degree in 2007.She is now a lecturer.Her research concerns electronic technology and signal processing.

An Improved Method for Fast Correcting Ionospheric Phase Contamination in Over-The-Horizon Radars

ZHANG Lidong,LI Jushang
(College of Optical and Electronic Information,Changchun University of Science and Technology,Changchun 130012,China)

The phase perturbation occurs when phase of over-the-horizon radar(OTHR)echo signal is modulated by the time-varying ionosphere and the echo spectrum is widened.The maximum likelihood estimation(MLE)method has better estimation performance of phase error than phase gradient autofocus (PGA)method.However,this method has a large amount of computation which limits the real-time application.In this paper,an improved MLE method is proposed based on the projection approximation subspace tracking approach.The improved method uses recursion algorithm to estimate the eigenvector of the maximum eigenvalue and avoids the eigenvalue decomposition process.The improved method has a comparable perturbation correcting performance to the MLE method and can significantly reduce computation. Theoretical analysis and simulation results show that the improved method has good universality for various forms of phase perturbation,the computation is only 1/10000 of MLE method,thus more available for engineering implementation.

over-the-horizon radar(OTHR);ionospheric phase contamination correction;maximum likelihood estimation(MLE);projection approximation subspace tracking(PAST)

1 引 言

天波超视距雷达(Over-The-Horizon Radar, OTHR)为大型阵列雷达,可以实现对800～3 500 km的地(海)面特性、海面舰船目标及地(海)面上空的飞行目标进行探测[1]。OTHR必须依靠电离层进行电波传播,不稳定的电离层将会使OTHR回波信号产生相位污染。相位污染有两种形式,一种是线性相位污染,它会使OTHR回波多普勒谱产生偏移,对目标检测结果影响不大;另一种是非线性相位污染,它会造成回波多普勒谱展宽[2],严重削弱OTHR系统对目标的检测性能。

The National Science and Technology Infrastructure Program(2012BHA12B01;2012BHA12B02)

**通信作者:ztg_1596@sina.com ztg_1596@sina.com

TN958

A

1001-893X(2016)11-1242-06

10.3969/j.issn.1001-893x.2016.11.011

2016-03-28;

2016-06-06

date:2016-03-28;Revised date:2016-06-06

国家科技支撑计划(2012BHA12B01;2012BHA12B02)

引用格式:张立东,李居尚.快速校正天波雷达电离层相位污染的改进方法[J].电讯技术,2016,56(11):1242-1247.[ZHANG Lidong,LI Jushang.An improved method for fast correcting ionospheric phase contamination in over-the-horizon radars[J].Telecommunication Engineering,2016,56(11):1242-1247.]