一种特殊GDOP场景下的NLOS传播识别算法*

邓水发,邓 平,芮 洋

(西南交通大学信息编码与传输重点实验室,成都610031)

一种特殊GDOP场景下的NLOS传播识别算法*

邓水发**,邓 平,芮 洋

(西南交通大学信息编码与传输重点实验室,成都610031)

在地面无线定位中,影响定位精度的最大因素是电波的非视距(NLOS)传播误差,定位估计前识别收发信机之间电波是视距(LOS)还是NLOS传播是提升定位精度需要研究的重要课题。为此,先对一种基于交叉面积的NLOS识别算法进行改进,然后提出了一种针对特殊几何精度因子(GDOP)场景下的NLOS识别算法——分步检验算法。该算法采用两步进行识别,先用数据检验筛选出测量样本中的LOS测量值,再用改进的交叉面积算法进行识别。仿真结果表明,分步检验算法在特殊GDOP场景下具有良好的识别性能。

地面无线定位;非视距传播;特殊GDOP;分步检验;识别算法;交叉面积算法

目前在研究NLOS场景下的定位问题时,通常假定距离测量值较多,侦测站在被定位目标周围, GDOP条件较好。但是在海岸、边境、战场等侦测站较少(最多4个侦测站),目标在侦测站组成的多边形外这种GDOP条件较差的特殊场景下(见本文的仿真场景),可供选择的测量值样本数也极少,NLOS误差对定位精度的不利影响会更大[7]。

为此,本文首先对一种交叉面积算法进行了改进,在此基础上提出了NLOS传播识别算法——分布检验算法,在特殊GDOP场景下取得了较好的LOS/NLOS识别性能。

2 NLOS系统模型

收发信机之间进行距离测量时,影响测距精度的误差主要源于设备测量误差和NLOS误差。一般认为NLOS误差远大于测量误差。假设系统中有N个侦测站,第i个侦测站到目标的测量距离可采用如下模型:

3 交叉面积算法

交叉面积算法由文献[10]提出,但该算法是基于蜂窝网络的场景,并不能直接应用于本文研究的特殊GDOP场景中。该算法根据LOS条件下相对于NLOS条件下3个基站构成的圆(以基站为圆心,测得的距离为半径)所形成的交叉面积较小的原理,找到一个门限面积STH,然后将交叉面积与STH相比较进行LOS/NLOS识别。

设一门限概率Pd=0.98,使得LOS条件下三基站的交叉面积在概率Pd下小于某门限面积 STH。LOS条件下3个基站测距的误差都是服从高斯分布的测量误差:e～N(0,σ2)。

假设ei小于r的概率等于P。3个基站的测量误差都达到r时,它们的交叉面积最大,近似形成如图1(a)所示以C为圆心、半径为r的圆,由此我们可以得到

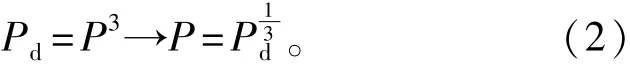
式中:P=Φ(z)为高斯累积分布函数值。可以求得r=zσ,那么近似的门限面积为

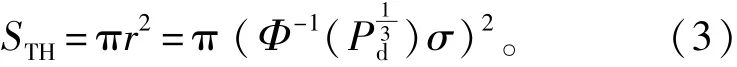
在实际的距离测量中,3个圆交叉所形成的形状并不规则,但近似看作是一个三角形,假设3个交叉点为(x1,y1)、(x2,y2)、(x3,y3),可以求得交叉面积

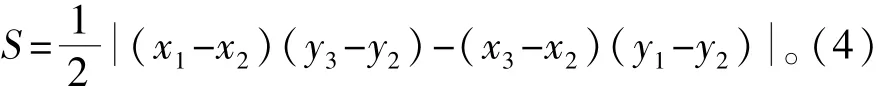
在特殊场景下,如图1(b)所示,所谓的交叉面积不是指它们的共同面积,而是不同两圆相交的3个交点之间最小的面积,无论在 LOS条件还是NLOS条件下,它们之间交叉的共同面积往往是非常大的,但在LOS条件下,会有3个点趋向于同一点,从而这3个点所围成的面积很小,选择该面积作为与门限面积STH相比的值。

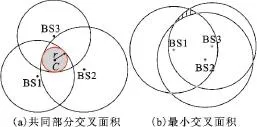
图1　交叉面积示意图Fig.1 Intersection area diagram

文献[10]通过判断小于门限面积的组合个数k进行识别,假设识别的LOS基站个数为m。

(1)k=0

由于没有组合的交叉面积小于STH,认为m＜3。

(2)1≤k≤3

设交叉面积的3个交点坐标分别为(x1,y1)、(x2,y2)、(x3,y3),目标位置估计为

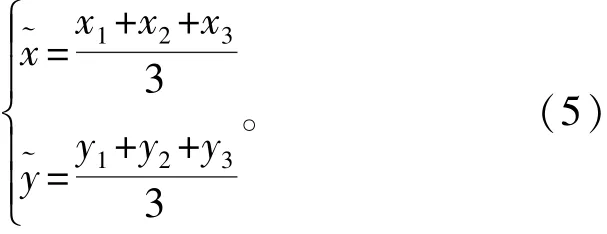
可以得到一个残差:

式中:(xi,yi)表示第i个基站的坐标;ri表示各个基站的测量距离;~ri=(x~-xi)2+(y~-yi)2。如果某个组合中全为LOS基站,那么

找出交叉面积小于STH且符合式(7)的组合集合{Si},算出集合中元素个数w。如果w=0,认为m＜3;如果w=1,则集合中唯一的组合的3个基站为LOS基站,如果w＞1,则将集合中交叉面积最小的3个基站判决为LOS基站。

(3)k≥4

计算第i个基站所在的组合(共有C2n-1个组合, n表示基站个数)中的交叉面积小于STH的组合个数t,如果t≥3则认为该基站为LOS基站,否则判定该基站为NLOS基站。

4 基于交叉面积的改进算法

本文研究只有4个侦测站的情况,文献[10]算法需要C34=4个组合的交叉面积全部小于STH才认为4个侦测站全为LOS传播的侦测站。侦测站较多时,组合数会成倍增加,包含某一个侦测站的组合数较多。但侦测站只有4个时,包含某一特定侦测站的组合只有C23=3个,样本较少,故文献[10]算法不适合这种特殊场景,对于特殊GDOP场景应当考虑小于STH的组合数k的每一种情况。假设侦测站个数为4,LOS侦测站个数为m,交叉面积小于STH的组合个数为k,本文进行粗略估计。

(1)当k=4时,很大概率上m=4。

(2)当k=1时,很大概率上m=3。

(3)当k=0时,最可能的是m＜3。

(4)当k=3时,假设m=4,则其中有一个组合的交叉面积大于STH,则

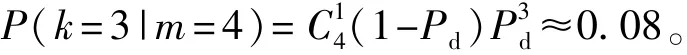
假设m=3,则pn表示包含NLOS侦测站的组合的交叉面积大于STH概率,如果P(k=3|m=3)＞0.08,则pn＜0.815,pn明显太小,不符合实际情况,所以m=4。

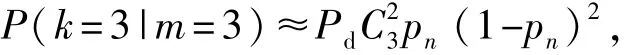
(5)当k=2时,则有

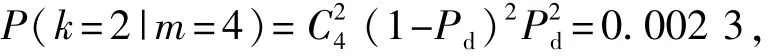
这个概率非常低,假设m=3时,假设pn=0.999,那么

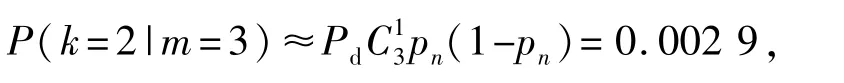
在很大的pn概率下,P(k=2|m=3)＞P(k=2|m= 4),故当k=2时,应当认为m=3。

通过上述分析判断,可得到以下判决:

当k=2时,还需要判断哪个组合为LOS组合,为此,本文采用数据检验(Data Test,DT)方法[6]进行处理。

假设某个组合中有3个侦测站,并且假设前2个侦测站为LOS传播,第3个侦测站的LOS/NLOS传播情况未知,这3个侦测站测得的距离为

式中:di表示侦测站到目标的视距距离;εi表示测量误差;ni为NLOS误差(n1=n2=0)。令

将式(9)写成矩阵形式可得

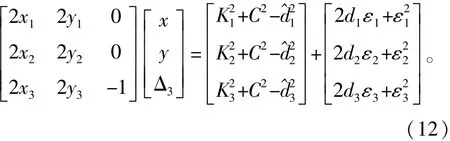
其中:

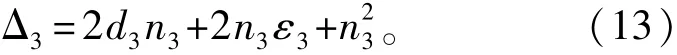
通过式(12)和式(13)可以求得Δ3。如果3个侦测站为LOS侦测站,即n3=0,那么Δ3≈0,否则Δ3＞0,通过Δ3可以判断3个侦测站视距与非视距可能的情况。

当1≤k≤2时,求出的LOS组合的交叉面积的3个交点应在第4个侦测站所形成的圆内,因为第4个侦测站为NLOS侦测站,其测得的距离应大于视距距离,否则判断该组合为LOS组合不成立。

5 分步检验算法

包含NLOS侦测站的组合的交叉面积也可能小于STH,造成一定的过判(判决的LOS侦测站数大于其实际个数),上面所述的算法很难进行判断。如图2所示,3个侦测站分别为C1、C2、C3,假设真实位置与测得的位置分别为P点、P′点,包含NLOS误差的测量值R′1、R′2、R′3组成的3个圆也交于一点P′,但离真实位置较远,误差较大。在这样的情况下,对于LOS侦测站比较少,而识别为LOS条件下的测量结果,我们需要通过多次测量进行判别,这就是本文提出的分步检验算法。

图2　LOS/NLOS三圆都交于一点示意图Fig.2 Diagram of three circles intersected at one point in LOS/NLOS situation

假定被定位目标位置在短时间内是静止的,对目标进行N次距离测量,测量模型如式(1)所示。

对第i个侦测站的N个测量值从小到大进行排序,令排序后的测量值序列表示为

式中:di1为最小值;diN为最大值。那么从统计学角度来讲,如果这N次测量数据全部为LOS测量值,那么它们的标准差应该不大于σ,然而,这些测量值中很可能存在一定的NLOS测量值。因为LOS测量值比NLOS测量值要小,那么Di中的值越排在前面为LOS测量值的概率就越大,假设Di中的第m+1个值开始带有NLOS误差,即

根据式(15),找到一个m,使得Di中前m个值的方差小于或者等于σ2,前m+l(1≤l≤N-m)个值的方差大于σ2。但是,找到m后也不能说明Di中前m个值都为LOS测量值,如果m比较小,也可以认为m之前的值都是NLOS测量值,所以需要一个门限M,使得m＞M时才认为前m个值都为LOS测量值。假设我们以测量样本中至少6%以上的测量值为LOS测量值才认为m之前的数据为LOS测量值,那么

将符合m＞M的侦测站进行组合求交叉面积,需要的距离用Di中前m个值的平均值¯di:

随机变量¯di的标准差σ′i为

式中:mi表示第i个侦测站的m值。由于mi是不一样的,但mi＞M成立,所以

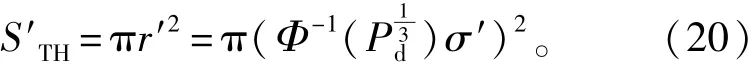
那么所有LOS条件下的组合的交叉面积应该在最小为Pd概率下小于S′TH。将满足m＞M的侦测站进行组合求交叉面积,假设这样侦测站个数为n,根据n的大小作不同的处理:

(1)当n＞3时,采用第4节所述的改进算法;

(2)当n=3时,则只有一个组合可以用来求交叉面积,将交叉面积与S′TH相比较,如果小于S′TH就按照上节中k=1的情况进行判决,否则认为LOS侦测站数小于3;

(3)当n＜3时,没有足够的侦测站来求交叉面积,那么认为LOS侦测站数小于3。

6 仿真结果及分析

仿真场景如图3所示,假设4个侦测站的坐标分别为(500,300)、(2 000,10)、(3 000,300)、(4 000,10),目标位于(2 500,2 000),单位均为m。为了避免NLOS侦测站位置对性能的影响,随机选取n个测量值为NLOS的侦测站。测量误差服从均值为0、标准差分别为10 m、15 m、20 m、25 m、30 m、35 m、40 m的高斯分布,NLOS误差服从0.05×d～0.9×d(d表示视距距离)之间的均匀分布,进行独立1 000次仿真实验。

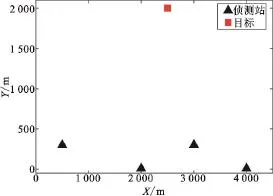
图3　侦测站与目标位置图Fig.3 Diagram of measuring stations and target position

6.1 交叉面积算法及其改进算法

仿真参数如表1所示,我们判断正确识别的标准为:当LOS侦测站数目为3个以上时,能将所有LOS侦测站分别识别出来为识别正确;当LOS侦测站数小于3个时,判决LOS侦测站数小于3为识别正确。

表1　交叉面积算法及其改进算法仿真参数Tab.1 Simulation parameters for the intersection area based algorithm and its improved algorithm

两种算法的正确识别次数如表2所示,其中n表示NLOS侦测站个数,σ为测量误差的标准差。

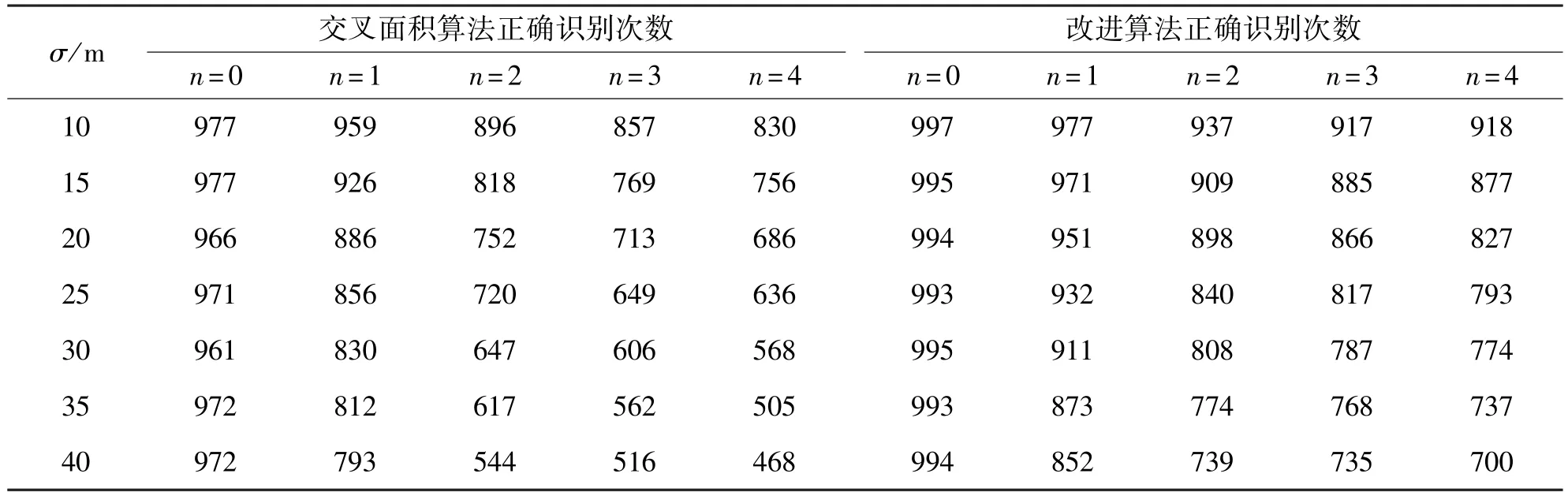
表2 交叉面积算法及其改进算法仿真结果Tab.2 Simulation results of the intersection area based algorithm and its improved algorithm

从仿真结果可以看出,两种算法对于全为LOS侦测站的情况下识别度非常高,测量误差参数对其性能影响不是很明显;存在NLOS侦测站时,其性能随着测量误差的标准差增大而明显下降,但改进算法正确识别的次数明显优于原算法。

6.2 分步检验算法

对于分步检验算法,仿真参数与前面的仿真参数一样,在每次仿真中,侦测站测量的数据样本个数为100,NLOS侦测站与LOS侦测站所测数据中产生的NLOS误差概率分别为100%和80%,即LOS侦测站数据样本中只有20%的LOS测量值,其LOS测量值越多,测量样本平均值越接近视距距离,我们选择一种条件较差的参数进行仿真实验。

正确识别标准与之前的标准一样,仿真结果如表3所示。

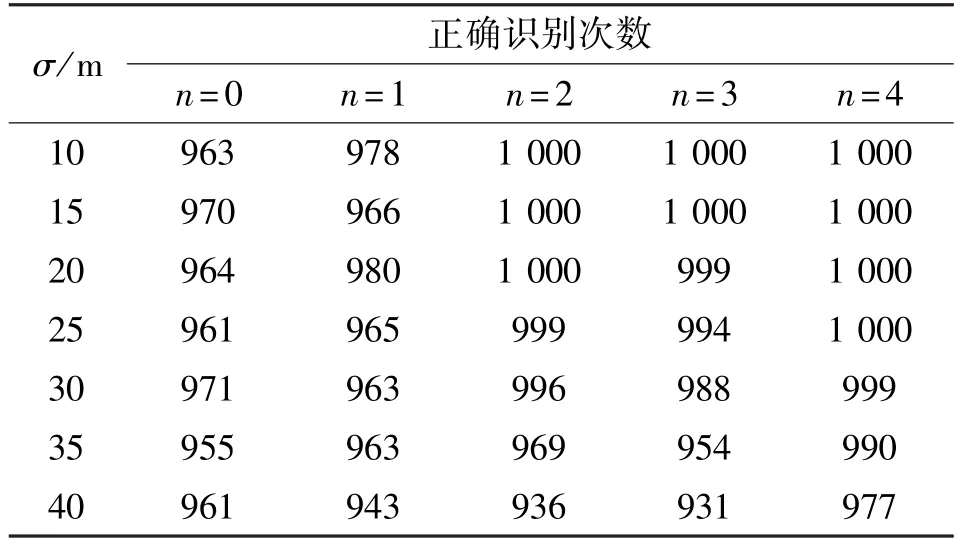
表3　分步检验算法仿真结果Tab.3 Simulation results of the step by step algorithm

从表3中可以看出,分步检验算法的正确识别性能明显得到更大幅度提升,且测量误差标准差对识别性能影响不大。

6.3 3种算法识别性能比较

为了直观比较本文中3种算法的识别性能,以标准差作为自变量,每种标准差下不同NLOS侦测站个数的正确识别概率的平均值作为因变量,结果如图4所示。从图4中可以看出,随着标准差的增大,分步检验算法的性能下降缓慢,其正确识别概率明显高于其他两种算法。

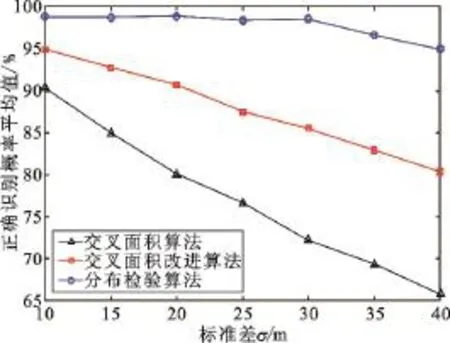
图4　三种算法性能比较Fig.4 Performance comparison among three algorithms

7 结束语

本文针对一种GDOP场景下LOS/NLOS测量值的识别问题开展研究,详细分析和改进了一种交叉面积的识别算法,在此基础上提出了一种分步检验算法,并通过仿真验证了分步检验算法对于识别性能提升的优良性。在算法计算复杂性方面,交叉面积计算最复杂的是圆与圆的交点,而分步检验算法的第一步过滤了一定的NLOS侦测站,使得NLOS侦测站没有与其他圆进行求交点的计算步骤,大大降低了算法计算复杂度,仿真实验过程也验证了这一点。

本文虽然是针对4个侦测站的情况进行讨论的,但本文算法也可以推广到其他情况。当只有3个侦测站时,相当于分步检验算法1个NLOS侦测站的情况;当有5个侦测站或者更多侦测站时,通过分布检验都可以先排除一定的NLOS传播的侦测站,然后再通过改进的交叉面积算法提高识别精度,其中小于门限面积的组合个数k可以根据原算法进行判断。

[1] CHEN P C.A non-line-of-sight error mitigation algorithm in location estimation[C]//Proceedings of 1999 Wireless Communications and Networking Conference. New Orleans,LA:IEEE,1999:316-320.

[2] LI X.An iterative NLOS mitigation algorithm for location estimation in sensor networks[C]//Proceedings of 15th IST Mobile&Wireless Communications Summit.Mykonos, Greece:IST,2006:1-5.

[3] ZHENG X N,HUA J Y,ZHENG Z L.LLOP localization algorithm with optimal scaling in NLOS wireless propagations[C]//Proceedings of 4th IEEE International Conference on Electronics Information and Emergency Communication.Beijing:IEEE,2013:45-48.

[4] XIAO Z,WEN H,MARKHAM A,et al.Non-line-ofsight identification and mitigation using received signal strength[J].IEEE Transactions on Wireless Communications,2014,14(3):1689-1702.

[5] TIAN S,ZHAO L,LI G.A support vector data description approach to NLOS identification in UWB positioning[J]. Mathematical Problems in Engineering,2014(1):1-6.

[6] CHAN Y T,TSUI W Y,SO H C.Time-of-arrival based locali-zation under NLOS conditions[J].IEEE Transactions on Vehicular Technology,2006,55(1):17-24.

[7] MUQAIBEL A H,AI-NIMNIM R A,LANDOLSI M A,et al.Mobile localization based on improved non-line-ofsight classification[C]//Proceedings of 29th International Conference on Thermoelectrics.Shanghai:IEEE,2010: 368-374.

[8] YU K,GUO Y J.Statistical NLOS identification based on AOA,TOA,and signal strength[J].IEEE Transactions on Vehicular Technology,2009,58(1):274-286.

[9] WANG Y,CHENG L,HU N.Bayes sequential test based NLOS localization method for wireless sensor network[C]// Proceedings of 2015 27th Chinese Control and Decision Conference(CCDC).Qingdao:IEEE,2015:5230-5234.

[10] KUANG L,HUANG J Y,YANG W L.Line-of-sight identification based on area measurements[C]//Proceedings of 2012 International Conference on Automatic Control and Artificial Intelligence(ACAI 2012).Xiamen: IET,2012:1306-1309.

邓水发(1990—),男,湖南衡阳人,硕士研究生,主要研究方向为无线定位中NLOS传播识别与误差减弱技术;

DENG Shuifa was born in Hengyang,Hunan Province,in 1990.He is now a graduate student. His research concerns NLOS identification and mitigation in wireless location.

Email:dengshuif.a@163.com

邓 平(1964—),男,四川宜宾人,教授,主要研究方向为无线传感网络定位技术、室内定位技术;

DENG Ping was born in Yibin,Sichuan Province,in 1964. He is now a professor.His research concerns wireless sensor networks for localization and indoor location.

芮 洋(1990—),男,江苏南京人,硕士研究生,主要研究方向为无线定位中NLOS传播识别与误差减弱技术。

RUI Yang was born in Nanjing,Jiangsu Province,in 1990. He is now a graduate student.His research concerns NLOS identification and mitigation in wireless location.

A NLOS Propagation Identification Algorithm for Special GDOP Scene

DENG Shuifa,DENG Ping,RUI Yang
(Key Laboratory of Information Coding and Transmission,Southwest Jiaotong University,Chengdu 610031,China)

In ground-based wireless positioning,a crucial factor influencing the positioning accuracy is the non-line-of-sight(NLOS)error of radio propagation.Before location estimation,determining the radio propagation between transmitter and receiver is LOS or NLOS is an important issue for improving positioning accuracy.Firstly,a NLOS identification algorithm based on intersection area measurements is improved.Then,for special geometric dilution of precision(GDOP)scene,a NLOS identification algorithm named step by step test algorithm is proposed.This algorithm realizes the NLOS identification by two steps. The LOS measurements are selected by data test(DT)method in the first step,and then the improved intersection area measurements algorithm is utilized to make the identification in the second step.The simulation results show that this algorithm possesses high identification performance under special GDOP scene.

ground-based wireless positioning;non-line-of-sight propagation;special GDOP;step by step test;identification algorithm;intersection area based algorithm

1 引 言

在城市环境中利用蜂窝基站对移动手机进行无线定位,以及海岸、边境、战场等场景利用地面侦测站对地面辐射源进行无线定位时,由于收发信机之间电波的非视距(Non-Line-of-Sight,NLOS)传播普遍存在,使得侦测站测得的距离通常为具有较大误差的NLOS距离,大于两者之间的视距距离,从而引起定位精度严重下降。降低NLOS是无线定位领域提高定位精度的一个重要课题,目前针对NLOS误差采用直接消除及先识别后消除两种方法处理。由于直接消除方法如残差加权算法[1]、迭代最小残差算法[2]、二次规划算法[3]等在 NLOS误差较大及LOS侦测站较少时很难取得满意的性能。本文主要研究后一种方法,通过先对电波的LOS/NLOS传播进行识别,再采用适当的NLOS误差减弱算法来提高定位精度。例如:对LOS测量值赋予更大的权值,或者定位估计时直接排除NLOS误差较大的测量值。在现有先识别后消除类算法中,基于信号特征算法[4-5],需要事先在某环境下进行大量的数据采集,记录某点的信号特征,然后建立一个数据库进行LOS/NLOS识别;基于位置残差算法[6-7]要求基站数量较多;基于先验概率算法[8-9]要求事先知道LOS发生概率和NLOS发生概率,同样需要事先的大量样本采集,这些算法还没能取得满意的性能。

**通信作者:dengshuif.a@163.com dengshuif.a@163.com

TN92

A

1001-893X(2016)11-1195-06

10.3969/j.issn.1001-893x.2016.11.003

2016-01-23;

2016-07-22

date:2016-01-23;Revised date:2016-07-22

引用格式:邓水发,邓平,芮洋.一种特殊GDOP场景下的NLOS传播识别算法[J].电讯技术,2016,56(11):1195-1200.[DENG Shuifa,DENG Ping,RUI Yang.A NLOS propagation identification algorithm for special GDOP scene[J].Telecommunication Engineering,2016,56(11):1195-1200.]