桥梁概率地震需求分析中的地震动强度指标选择研究

陈 敏

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)



桥梁概率地震需求分析中的地震动强度指标选择研究

陈 敏

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

对目前桥梁抗震分析和设计中应用较多的两个地震动强度指标，即峰值地面运动加速度(PGA)和结构特定周期处的谱加速度(Sa)，研究在基于性能的地震工程学理论中，采用PGA和Sa作为地震动强度指标，对非规则连续梁桥概率地震需求分析的重要影响。

基于性能的地震工程学；概率地震需求分析；地震动强度指标；实际地震波

1 概 述

美国太平洋地震工程研究中心(Pacific earthquake engineering research center,PEER)提出的新一代基于性能的地震工程学理论框架(Performance-based engineering research,PBEE),已被国际上公认为未来结构抗震设计理论的发展方向,并逐步应用于桥梁抗震设计,建立了基于性能的桥梁抗震设计理论(Performance-based seismic design,PBSD)。PBEE和PBSD理论由四个性质不同却紧密联系的分析阶段组成[1-2],包括概率地震风险分析[3-4]、概率地震需求分析[5-6]、概率地震破坏分析[7]和概率地震损失分析[2]。其中,概率地震需求分析(Probabilistic seismic demand analysis,PSDA)是PBEE和PBSD理论的重要一环,通过PSDA可以对不同地震风险水平下的结构地震需求进行概率预计,从而建立概率地震需求模型,形成工程需求参数风险曲线等计算结果,而地震动强度指标(Intensity measure,IM)的合理选择是影响概率地震需求分析精确度的一个重要因素[8-10]。

2 桥梁实例

本文选择某高速公路上一座变墩高非规则连续梁桥作为算例桥梁,其上部结构为预应力混凝土连续箱梁,下部墩柱结构为独柱,墩高分别为8、10、15、10和8 m,跨径组合为40 m+60 m×4+40 m=320 m。算例桥梁有限元模型的建立以及动力分析均采用有限元分析软件OpenSees[2]来实现。主梁采用弹性梁单元模拟;桥墩采用考虑沿单元长度分布塑性的基于力的非线性梁柱单元进行模拟,桥墩截面采用纤维单元进行离散。算例桥梁纵桥向活动支座采用聚四氟乙烯板式橡胶支座,在地震作用下其恢复力-位移模型可以用双线性来表示,并通过土弹簧考虑土-结构相互作用。算例桥梁有限元模型见图1所示。

图1 算例桥梁有限元模型

通过算例桥梁结构动力特性分析,将桥梁在纵桥向和横桥向模态质量参与系数贡献显著的模态列于表1中。分析可知,在横桥向有两阶模态振型的质量参与系数较大,分别达到了0.674和0.211,说明在横桥向存在高模态效应。

表1 算例桥梁动力特性

3 概率地震风险分析

峰值地面运动加速度(PGA)和结构特定周期处的谱加速度(Sa)是目前桥梁抗震设计中使用最广泛的两种地震动强度指标(IM),且国内外结构抗震规范也基本采用PGA和Sa作为IM。因此,本文分别采用PGA和横桥向模态质量参与系数最大的一阶谱加速度Sa(T2)作为IM,分析PGA和Sa对于非规则连续梁桥概率地震需求分析的适用情况。

通过概率地震危险性分析[5]可以获得桥址工程场地对应于四个不同水准的地震作用,即50年63%、50年10%、50年5%和50年2%超越概率的地震作用,并能获得相应的水平设计地震动加速度一致风险反应谱(阻尼比为0.05),具体见图2。将四条一致风险反应谱作为目标谱,以PGA作为IM,通过调幅,共选择四组原始的实际地震波分别模拟不同超越概率地震水准下的地震动。

图2 50年2%、5%、10%、63%超越概率下的一致风险反应谱

在地震工程学中,50年63%、50年10%、50年5%和50年2%超越概率下的地震危险性水平对应的平均回归期分别是50年、474年、975年和2 475年,由于假定IM服从对数正态分布[7],根据回归期与地震动强度指标在双对数坐标系下的线性拟合可以获得工程场地的地震风险曲线,即建立了桥工程场地的地震灾害模型,具体见公式(1),公式中k和k0为回归系数。

(1)

通过上面的分析可以求得PGA作为IM时,k和k0分别为2.145 63和0.000 025 4,Sa(T2)作为IM时,k和k0分别为1.890 44和0.000 053 1。

4 概率地震需求分析

考虑到连续梁桥的主要破坏形式,本文采用墩顶漂移比作为工程需求参数(Engineering demand parameter,EDP),即在地震过程中,墩顶最大绝对位移与桥墩高度之比,反映了桥墩结构在地震作用下的最大变形能力(延性)。

以中墩为例,分别采用PGA和Sa(T2)作为IM时,四组地震波对于结构地震需求的概率预计结果具体见表2。分析可知,两种IM在同一地震风险水平下的EDP均值预计较为接近,说明对于桥梁地震响应预计较为一致。但PGA作为IM时,EDP概率预计的离散度比Sa(T2)略小,这主要是因为在地震波选择时,是按照PGA作为IM进行调幅并选波的,如果采用Sa(T2)作为IM进行调幅并选波,其EDP离散度一般均小于PGA作为IM(表2)。

表2 采用PGA和Sa(T2)作为IM时中墩EDP概率预计的统计分析表

在特定IM水平下假定工程需求参数(EDP)的概率分布服从对数正态分布,在概率地震需求分析中,需要将EDP表示为IM的函数,建立IM-EDP之间的数学关系,即概率地震需求模型,具体见(2)式。

(2)

将算例桥梁边墩、次边墩及中墩的墩顶漂移比与地震动强度指标在双对数坐标系下进行线性拟合,可以推导出IM与EDP之间的数学关系,即概率地震需求模型(表3)。

表3 不同桥墩的概率地震需求模型

概率地震需求分析的主要目的是桥梁的EDP风险曲线,即在特定IM水平下,EDP超越特定值的概率λ(EDP>edp|IM),从而对工程场地桥梁结构地震响应水平进行概率预计,EDP风险曲线的计算公式具体见(3)式。

λ(EDP>edp|IM)=

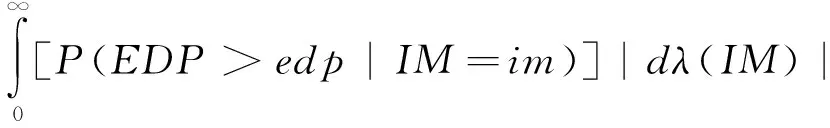
(3)

结合地震灾害模型和概率地震需求模型,可对(3)式进行积分,获得EDP风险曲线,见(4)式。

(4)

分析图3～5可知,对于同样的EDP水平,PGA作为IM的年平均超越概率要明显小于Sa(T2)作为IM,因此,PGA作为IM对桥梁地震响应水平的预计可能会偏于非保守,这对于桥梁抗震设计显然是不利的。而且,EDP风险曲线的预计精确性会显著影响到地震易损性曲线的精确性,从而对PBEE和PBSD的正确实施产生重要影响。

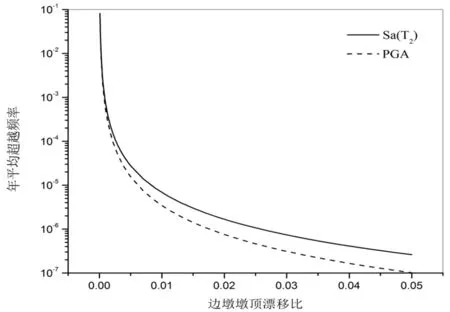
图3 边墩的墩顶漂移比风险曲线

图4 次边墩的墩顶漂移比风险曲线

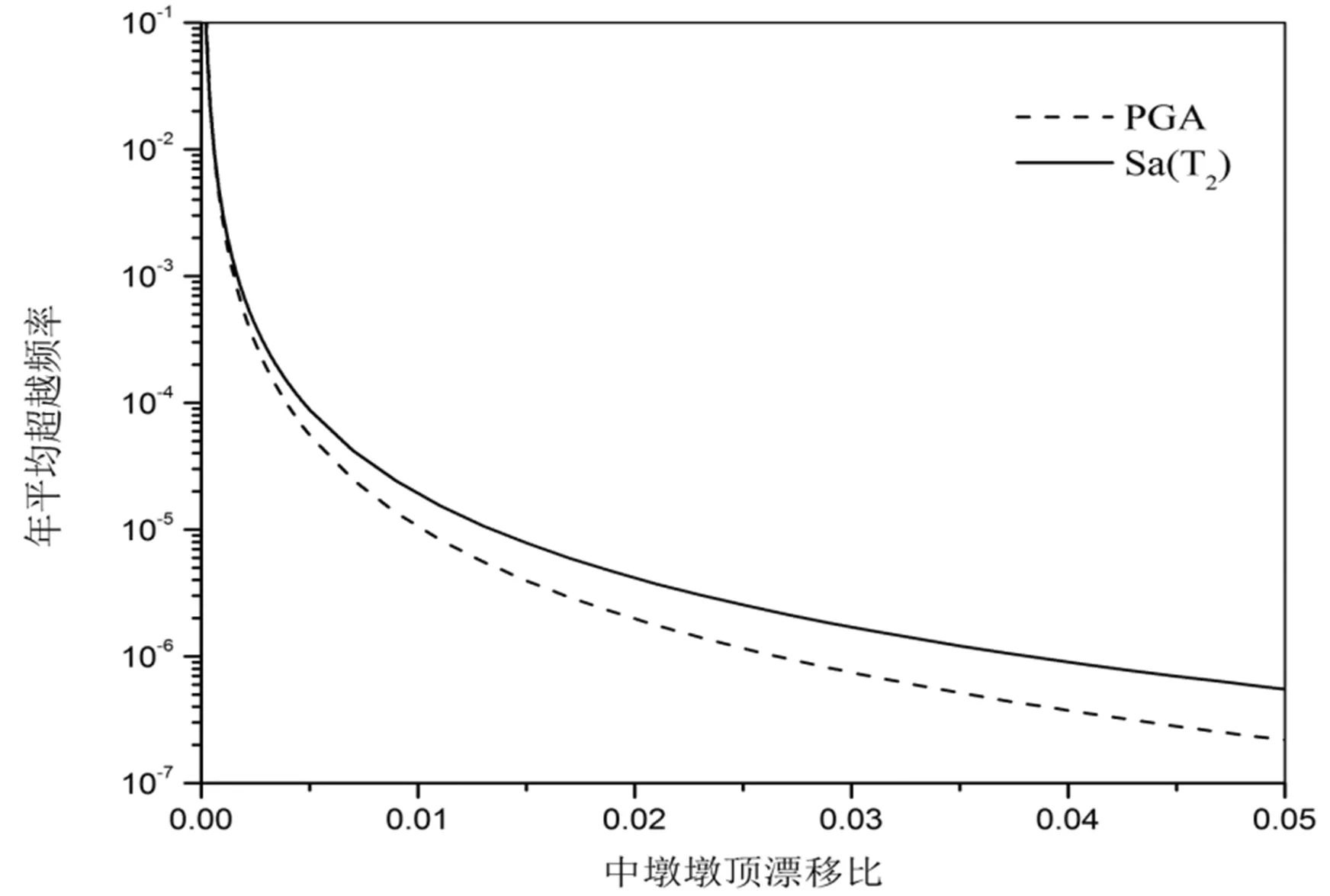
图5 中墩的墩顶漂移比风险曲线

5 结束语

由于非规则连续梁桥存在高模态效应,采用结构特定周期处的谱加速度(Sa)作为IM时,可以在一定程度上考虑到反应谱对于桥梁结构地震响应的重要影响。因此,采用Sa作为IM对结构地震需求、EDP风险曲线等的预计精度要高于峰值地面运动加速度(PGA)。而且,PGA作为IM对桥梁地震响应水平的预计可能会偏于非保守,这对于桥梁抗震设计显然是不利的。

但是,单个周期处的谱加速度作为IM,不能充分考虑到高阶模态振型对于结构地震响应的影响,因此,可以采用多阶模态周期处的谱加速度组成多参数地震动强度指标,更好地实施基于性能的非规则连续梁桥抗震设计。

[1] Pacific Earthquake Engineering Research Center [OL]. http://peer.berkeley.edu/. 2016.

[2] Sashi K K. Application of the PEER PBEE Methodology to the I-880 Viaduct [R]. Pacific Earthquake Engineering Research Center College of Engineering University of California, Berkeley. PEER Report 2006/10.

[3] McGuire R K.REVIEW Probabilistic seismic hazard analysis: Early history [J]. Earthquake Engineering and Structural Dynamics. 2008(37):329～338.

[4] Bazzuro P,Cornell A C.Disaggregation of Seismic Hazard[J].Bull. Seism. Soc. Am. 1999(89):501～520.

[5] Kevin M,Bozidar S. Seismic Demands for Performance-Based Design of Bridges [R]. Pacific Earthquake Engineering Research Center College of Engineering University of California, Berkeley. PEER Report 2003,8.

[6] 曾志和，樊 剑，余倩倩．基于性能的桥梁结构概率地震需求分析[J]．工程力学，2012，29(3):156～162.

[7] Singhal A, Kiremidjian A. Method of probabilistic evaluation of seismic structural damage [J]. Journal of Structural Engineering, ASCE, 1996,122(12):1459～1467.

[8] 陈 亮.地面运动特性对典型桥梁结构地震需求的影响研究[D].上海：同济大学，2009.

[9] 叶列平,马千里,缪志伟.结构抗震分析用地震动强度指标的研究 [J].地震工程与工程振动，2009,29(4):9～22.

[10] Jamie E P,Bryant G N, Reginald D.Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios [J]. Earthquake Engineering And Structural Dynamics，2008(37):711～725.

2016-04-27；修改日期：2016-05-03

陈 敏(1989-)，男，安徽安庆人，合肥工业大学硕士生．

U442.55

A

1673-5781(2016)03-0355-03