前混合水射流喷嘴流场的数值模拟

董 星， 刘雨庆， 李金林

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)



前混合水射流喷嘴流场的数值模拟

董 星， 刘雨庆， 李金林

(黑龙江科技大学 机械工程学院， 哈尔滨 150022)

为了获得前混合水射流喷嘴内外流场的流动特性，利用Fluent软件对喷嘴内外流场进行数值模拟。根据射流特性，数值模拟中湍流模型选用标准k-ε模型，液固两相流动采用欧拉模型，分析不同喷丸压力下水流场和弹丸流场最大轴向动压强和最大轴向速度的变化规律以及外流场中不同靶距对流场轴向速度的影响。结果表明：在内流场，喷嘴出口处流场最大轴向动压强和最大轴向速度随着喷丸压力的增加而增大，且同一喷丸压力条件下水流场最大轴向动压强小于弹丸流场最大轴向动压强，水流场最大轴向速度大于弹丸流场最大轴向速度；在外流场，水流场和弹丸流场最大轴向速度随着靶距的增加而减小。

前混合水射流； 喷嘴； 流场； 数值模拟

前混合水射流喷丸强化技术是近十几年来迅速发展起来的一项新技术，它的应用范围日益广泛，目前已应用在机械、水力及石油等众多领域[1-3]。其基本原理是将前混合水射流携带的巨大能量以特定的方式高速喷射到金属零构件表面上，使零构件表层材料在再结晶温度下产生塑性形变，呈现出理想的组织结构和残余应力分布，以达到提高零构件周期疲劳强度及抗应力腐蚀的目的[4]。

喷嘴是前混合水射流喷丸强化系统中将工作介质的压能转化为动能的关键元件，其性能直接影响射流品质和喷丸强化质量。喷嘴流场始终是水射流工作者研究的热点问题之一。但由于喷嘴喷出的混合水射流是紊态的复杂流动，所以理论分析难以求得高精度的解析解，实验测量难度较大、成本高，而计算流体动力学的发展为解决这一问题提供了有效方法[5-8]。因此，笔者应用Fluent软件对喷嘴全流场进行数值模拟，探究喷丸压力及靶距对水流场和弹丸流场的影响，拟为研究前混合水射流喷丸强化喷嘴流场流动特性提供技术基础。

1 基本模型及计算方法

1.1 几何模型

采用Pro/E软件建立前混合水射流喷嘴的几何模型，如图1所示。模型的总长度为64.3 mm，喷嘴入口圆柱段长度为10 mm，入口直径为7 mm；圆锥收敛段长度为9.3 mm，收敛角为30°；喷嘴出口圆柱段长度为5 mm，出口直径为2 mm，外流场取直径和长度均为40 mm的圆柱体。

图1 几何模型

1.2 有限元模型

将几何模型导入Fluent软件前处理器Gambit中，利用Gambit模块生成网格。本文采用多元化网格结构，采用Tet/Hybrid(主要由四面体网格构成，包含六面体、锥形和楔形网格单元)网格，并对外流场网格细分，提高仿真的稳定性和收敛性。网格划分后的单元数为1 334 512个，节点数为163 088个，几何模型划分网格后的有限元模型如图2所示。

图2 有限元模型

1.3 数学模型

文中研究的前混合水射流喷丸喷嘴中弹丸粒子体积分数大于10%，因此，采用多相流动模型中的欧拉模型模拟液固两相流动。

1.3.1 控制方程

流体运动受到物理守恒定律的约束，无论是定常或非定常流动、层流或湍流都遵循质量守恒定律、动量守恒定律、能量守恒定律，这些守恒定律在流体力学中分别对应着质量守恒方程、动量守恒方程、能量守恒方程。

(1)质量守恒方程

任何流动都必须满足质量守恒定律，以质量守恒方程体现，它的守恒形式表达式为

(1)

式中：ρ——密度，kg/m3；

t——时间，s；

u、v、w——速度矢量在x、y、z方向的分量，m/s。

(2)动量守恒方程

动量守恒定律也是任何系统都需要满足的基本定律，按照这一定律，在x、y和z三个方向的动量守恒方程分别为

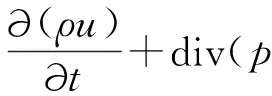
(2)

(3)

(4)

式中：p ——微元体上的压力，Pa；

μ——动力黏度；

ū——速度矢量，m/s；

Su、Sv、Sw——动量守恒方程的广义源项。

(3)能量守恒方程

能量守恒定律是包含热交换的流动系统必须满足的定律，对应的能量守恒方程为

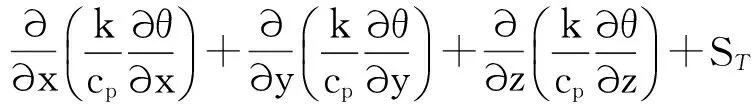
(5)

式中：cp——比热容，J/(kg·℃)；

θ ——温度，℃；

k——流体传热系数；

ST——黏性耗散项。

1.3.2 湍流模型

湍流是一种复杂的、无规则的运动，湍流模型主要包括雷诺应力模型和涡粘模型中的零方程模型、一方程模型和两方程模型。在两方程模型中，标准k-ε两方程模型是目前使用最广泛的湍流模型，它是在湍动能k方程的基础上，再引入一个关于湍动耗散率ε的方程。标准k-ε模型中湍动黏度μt是k和ε的函数：

(6)

式中：Cμ——经验常数。

在标准k-ε模型中，k和ε是两个基本未知量，其方程为

Gk+Gb-ρε-YM+Sk，

(7)

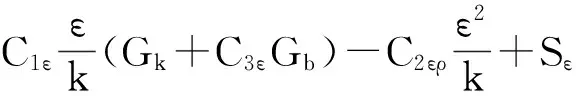
(8)

式中：Gk——平均速度梯度引起的湍动能k的产生项；

Gb——浮力引起的湍动能k的产生项；

YM——可压湍流中脉动扩张的影响；

Sk、Sε——用户定义的源项；

C1ε、C2ε、C3ε——经验常数；

σk、σε——湍动能k和耗散率ε对应的Prandtl数。

1.4 计算方法及边界条件

计算方法：Fluent计算求解中选择三维单精度求解器，采用一阶精度迎风差分格式，基于液固两相体积分数的湍流控制方程，压力速度耦合采用简单的相耦合法。亚松弛因子均取默认值，收敛判据为流场迭代的残差R≤10-3。

边界条件：喷嘴入口边界条件为压力入口，出口边界条件为压力出口；其值为当地大气压。在固体壁面上速度满足无滑移条件，近壁面区域采用标准壁面函数法。弹丸与水处于湍流流动，湍流模拟采用标准k-ε模型，考虑到液固两相流体的特点，计算流场采用欧拉模型。

2 模拟结果及分析

采用粒径为0.04 mm的弹丸，分别以4、6、8、10和12 MPa的喷丸压力进行喷丸，研究不同喷丸压力对喷嘴出口处流场的轴向动压强和轴向速度的影响。

2.1 喷丸压力对水流场的影响

图3为喷丸压力8 MPa时水流场轴向动压强ps分布云图。由图3可知，在内流场，水流场经过喷嘴圆锥收敛段，水流场的轴向动压强逐渐增加，在喷嘴出口处达到最大值；进入外流场由于截面积发生突变，受射流卷吸空气的作用，水流场轴向动压强迅速降低。

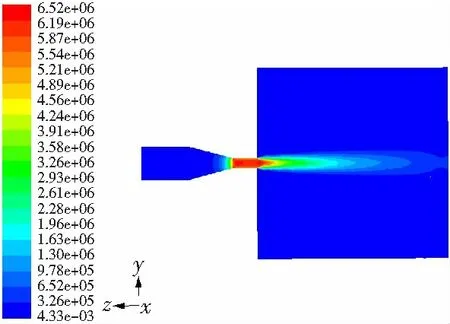
图3 水流场轴向动压强分布云图

图4为喷丸压力8 MPa时水流场的轴向速度vs分布云图。由图4可知，在内流场，水流场在刚进入喷嘴入口圆柱段时，由于横截面积没有发生变化，水流场轴向速度没有明显增加。经过喷嘴圆锥收敛段时，由于收敛角的加速作用使水流场的轴向速度逐渐增加。在外流场，由于射流卷吸空气的作用，水流场轴向速度逐渐减小直到打到靶体表面。

表1给出了喷丸压力po分别为4、6、8、10和12 MPa所对应的喷嘴出口处水流场的最大轴向动压强pmax和最大轴向速度vmax。图5和图6分别给出了最大轴向动压强和最大轴向速度随喷丸压力的变化关系。由图5和图6可知，以不同喷丸压力进行喷丸时，水流场的最大轴向动压强和最大轴向速度随喷丸压力的增加而讯速增大。

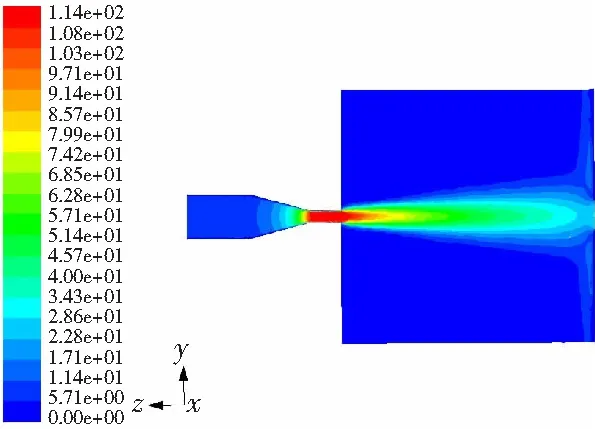
图4 水流场轴向速度分布云图

表1 不同喷丸压力对应的水流场最大轴向动压强和最大轴向速度

Table 1 Maximum axial dynamic pressure and maximum axial velocity under different peening pressure

po/MPapmax/MPavmax/m·s-143.2580.6464.8898.8386.52114.20108.14127.67129.77139.87

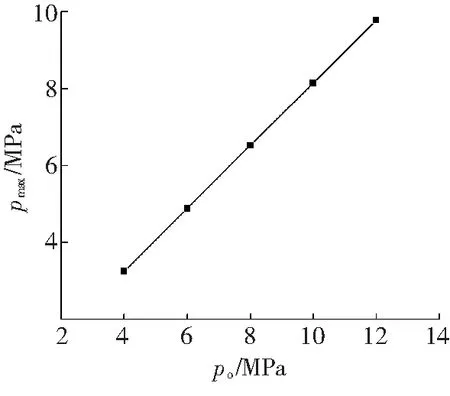
图5 水流场轴向动压强随喷丸压力的变化关系

Fig. 5 Relationship between axial dynamic pressure changing with peening pressure

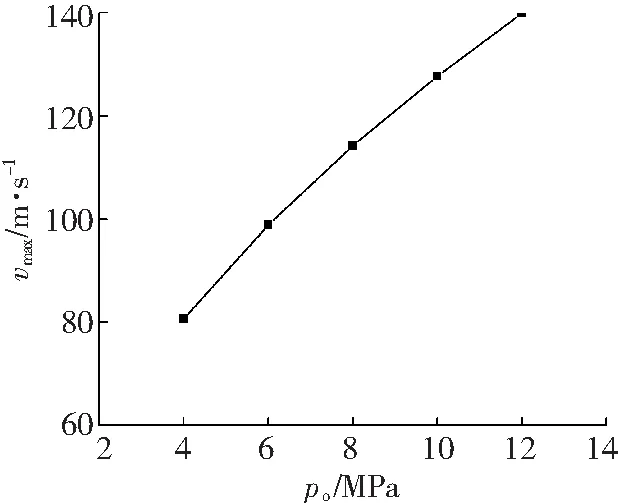
图6 水流场轴向速度随喷丸压力的变化关系

Fig. 6 Relationship between axial velocity changing with peening pressure

2.2 喷丸压力对弹丸流场的影响

图7为喷丸压力8 MPa时弹丸流场轴向动压强pd分布云图。由图7可知，在内流场，弹丸与水混合一起进入喷嘴入口，弹丸流场轴向动压强与水流场轴向动压强变化趋势相同，也是逐渐增加；但弹丸流场轴向动压强在圆锥收敛段增加的速率大于在圆柱段增加的速率。在外流场，弹丸流场的轴向动压强由于受到射流卷吸空气的作用而逐渐减小。

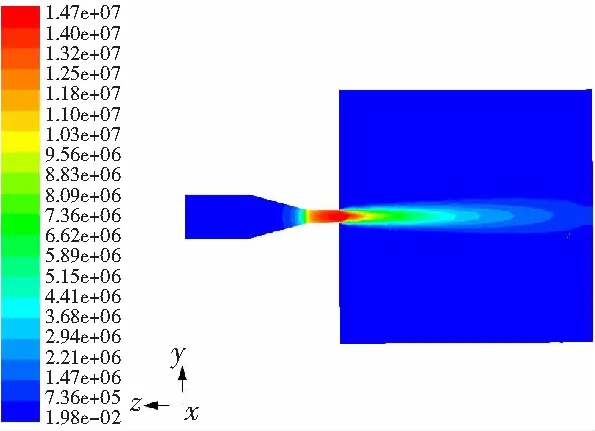
图7 弹丸流场轴向动压强分布云图

图8为喷丸压力8 MPa时弹丸流场轴向速度vd分布云图。由图8可知，在内流场，弹丸流场在进入喷嘴入口圆柱段时，喷嘴入口边界条件为压力入口，水流场还没有明显的速度变化，水流场对弹丸的加速作用有限。在进入喷嘴圆锥收敛段时，由于水流场的速度增加使得对弹丸流场的加速作用逐渐增大，弹丸流场的轴向速度逐渐增大，但由于弹丸粒子为固相，惯性大，水流场对其加速比较缓慢。因此在喷嘴出口处，弹丸粒子的速度小于水流速度。在外流场，同样由于弹丸粒子的惯性作用，弹丸流场会有一段过程速度逐渐减小直到靶体表面，且弹丸速度衰减比水流速度衰减慢。

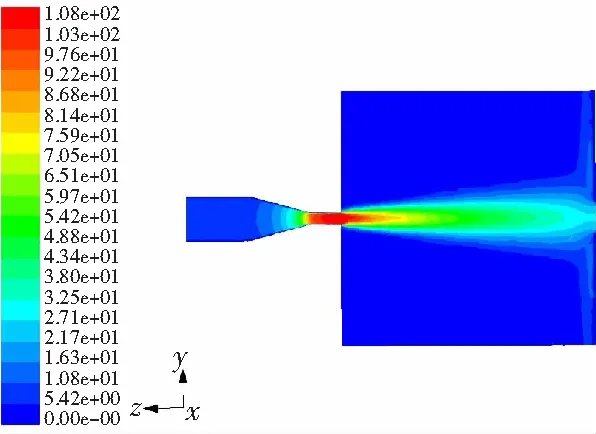
图8 弹丸流场轴向速度分布云图

表2给出了喷丸压力分别为4、6、8、10和12 MPa所对应的喷嘴出口处弹丸流场的最大轴向动压强pdmax和最大轴向速度vdmax。图9给出了弹丸流场最大轴向动压强随喷丸压力的变化关系。由图9可知，以不同喷丸压力进行喷丸时，弹丸流场轴向动压强随着喷丸压力的增加逐渐增大。图10给出了弹丸流场最大轴向速度随喷丸压力的变化关系。由图10可知，以不同喷丸压力进行喷丸时，弹丸流场轴向速度随着喷丸压力的增加逐渐增大。相同喷丸压力时，水流场的轴向动压强小于弹丸流场的轴向动压强；水流场的轴向速度大于弹丸流场的轴向速度。

表2 不同喷丸压力对应的弹丸流场最大轴向动压强和最大轴向速度

Table 2 Maximum axial dynamic pressure and maximum axial velocity under different peening pressure

po/MPapdmax/MPavdmax/m·s-147.4177.04611.0694.10814.71108.501018.33121.111221.90132.48

图9 弹丸流场轴向动压强随喷丸压力变化关系

Fig. 9 Relationship between axial dynamic pressure changing with peening pressure

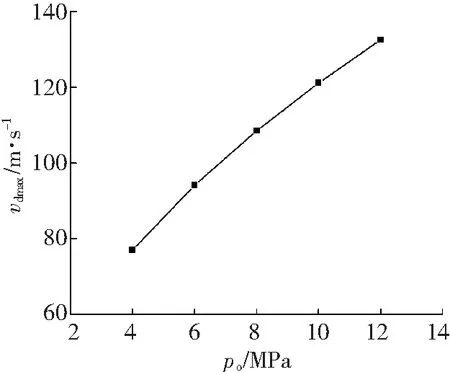
图10 弹丸流场轴向速度随喷丸压力的变化关系

Fig. 10 Relationship between axial velocity changing with peening pressure

2.3 靶距对外流场的影响

取喷丸压力8 MPa，弹丸直径0.04 mm，靶距D分别为0、10、20、30和40 mm进行数值模拟。

图11为喷丸压力8 MPa、靶距在10 mm时外流场的轴向速度分布云图。由图11可知，水流场和弹丸流场的轴向速度分布相似，由于射流卷吸空气的作用，射流中心处的速度最大，沿截面径向逐渐减小，射流外围处轴向速度最小。

a 水流场

b 弹丸流场

表3为不同靶距所对应的外流场最大轴向速度。图12给出了外流场轴向速度vm随靶距D变化的关系。

表3 不同靶距对应的流场最大轴向速度

Table 3 Maximum axial velocity of flow field under different target distance

D/mmvm/m·s-1水流场弹丸流场0114.20108.501091.3692.222062.8165.093045.6848.824034.2637.97

由图12可知，同一压力条件下，随着靶距的增加，水流场和弹丸流场的最大轴向速度都逐渐减小；由于惯性作用弹丸速度比水速度减小慢，且在靶距为0 mm时，水流场和弹丸流场的轴向速度最大。

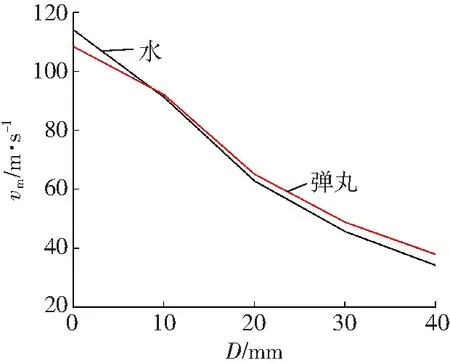
图12 流场轴向速度随靶距变化关系

Fig. 12 Relationship between axial velocity changing with target distance

3 结 论

(1)喷嘴水流场和弹丸流场的最大轴向动压强和最大轴向速度随着喷丸压力的增加而增大。在内流场，水流场和弹丸流场的轴向速度呈轴对称分布，且在喷嘴圆锥收敛段速度开始增加；在外流场，水流场和弹丸流场的最大轴向速度逐渐减小。在喷丸压力相同时，喷嘴出口处的水流场轴向动压强小于弹丸流场轴向动压强，水流场最大轴向速度大于弹丸流场最大轴向速度。

(2)水流场和弹丸流场最大轴向速度随着靶距的增加而逐渐减小，且流场都逐渐向外扩散，对靶体的作用面积逐渐增大。在靶距过大时，流场速度损失严重，对靶体表面作用面积变小。在靶距为0 mm时，水流场和弹丸流场的轴向速度最大。

[1] 董 星, 张贺明, 刘 文, 等. 前混合水射流喷丸强化喷嘴流场的数值模拟[J]. 黑龙江科技大学学报, 2015, 25(4): 399-404.[2] 董 星, 杨 威, 李光煜. 欧拉模型的后混合水射流喷丸喷头内流数值模拟[J]. 黑龙江科技大学学报, 2014, 24(4): 206-210. [3] 吉春和. 前混合磨料水射流喷丸强化技术[J]. 煤矿机电，2008(5)： 72-73.

[4] 吕国庆， 张新民. 前混合水射流强化技术及发展[J]. 机械工程与自动化， 2010(3)： 215-216.

[5] 董 星， 王瑞红， 段 雄. 前混合水射流喷丸表面粗糙度的试验研究[J]. 煤炭学报， 2009， 34(10)： 1410-1415.

[6] 吉春和， 张新民. 高压水射流强化技术及发展[J].材料热处理， 2007， 36(24)： 86-89.

[7] CH ILLMAN ALEX, RAMULU M, HASHISH M. Water jet and water-air jet surface processing of a titanium alloy: a parametric evaluation [J]. Journal of Manufacturing Science and Engineering, 2010, 13(1): 11-12.

[8] 董 星， 段 雄. 高压水射流喷丸强化技术[J]. 表面技术，2005， 34(1)： 48-49.

(编校 李德根)

Numerical simulation of nozzle flow field of premixed water jet

DongXing，LiuYuqing，LiJinlin

(School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper is motivated by the need for obtaining the flow characteristics of the inner and outer flow field of the former mixed water jet nozzle, using the Fluent software to perform the numerical simulation the inner and outer flow field of the nozzle. The study building on the characteristics of jet involves the numerical simulation of turbulence model using standardk-εmodel, liquid-solid two-phase flow using the Euler model; an analysis of the variation of maximum axial dynamic pressure and maximum axial velocity in the water and projectile flow field under different shot peening pressure; and an analysis of the influence of different target distance on the axial velocity of the flow field in the external flow field. The results show that along with an increase in shot peening pressure comes an increase in the inner flow field, flow field at the nozzle exit maximum axial dynamic pressure and the maximum axial velocity; and given the same shot peening pressure, water flow field has a smaller maximum axial dynamic pressure than projectile flow maximum axial dynamic pressure and a greater maximum axial velocity than the maximum axial velocity in flow field of projectile; in the outflow field, the increase inthe target distance is followed by a decrease in the maximum axial velocity of the flow field and the velocity of the projectile.

pre-mixed water jet; nozzle; flow field; numerical simulation

2016-08-26

黑龙江省教育厅科学技术研究项目(12531569)

董 星(1964-)，男，河北省滦平人，教授，博士，研究方向：水射流技术及流体机械设计理论，E-mail：dongxingwrh@163.com。

10.3969/j.issn.2095-7262.2016.05.018

TP69

2095-7262(2016)05-0558-06

A