黄河宁夏段干支流非一致性洪峰遭遇风险分析
2016-12-08李子远苑希民
李子远,冯 平,苑希民
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
黄河宁夏段干支流非一致性洪峰遭遇风险分析
李子远,冯 平,苑希民
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
对黄河和清水河非一致性洪峰进行遭遇风险分析。采用综合诊断法对洪峰序列进行变异性诊断,引入混合von Mises 分布和混合P-Ⅲ分布对洪峰发生时间和洪峰量级进行拟合;选择非对称部分嵌套Archimedean Copula函数,构建两河洪峰联合分布并分析两河洪峰发生时间和量级遭遇情况,绘制各种频率组合遭遇概率分布图。结果表明:两河洪峰序列均发生变异,两河洪峰发生时间遭遇概率在7月31日和8月31日达到最大,分别为3.36×10-4和1.15×10-4;不同频率洪峰遭遇概率在7月26日至8月2日和8月31日至9月5日两个时段达到最大。
洪峰遭遇;非一致性;混合分布;Copula函数;风险分析;黄河;清水河
特大洪水往往是由多来源洪水共同作用形成的,特别是流域性大洪水,各干支流洪水之间的相互影响尤为突出。目前水文工作中常用方法是将各来源洪水视为不相关,对洪水实测资料进行统计分析,该做法忽略了同流域内不同来源洪水之间的内在联系,所得结果显然不能准确描述实际洪水特征,且只能定性分析干支流遭遇情况,无法分析设计洪水情况。因此,综合考虑干支流洪水内在联系,定量分析干支流洪水遭遇概率,对河道防洪和水库调度有着重要意义。
Copula函数能很好地描述多变量之间的相依性,作为连接函数,具有形式多样化且不受分布函数限制、在变量单调变换下形式不发生变化等特点,被越来越广泛地用来对存在相关性的洪水序列进行联合分析[1]。Yan等[2]通过构建非对称三变量Clayton Copula函数对南水北调中线供水区和受水区降水丰枯遭遇概率进行分析,计算了极端降水条件下输水概率;Genest等[3]构建Meta-elliptical Copula函数对Romaine河春汛的洪峰、洪量和持续时间进行了联合频率分析;Chen等[4]构建X-Gumbel Copula函数分别对长江上游和Colorado河上游洪峰遭遇概率进行了分析。
气候环境变化和人类活动的影响导致部分流域水文序列的一致性遭到破坏,直接用实测数据进行边缘分布拟合会降低计算结果可靠性,因此必须进行水文序列变异性检验,并对发生变异的序列进行一致性处理。Zhang等[5]采用Mann-Whitney U检验法和累积离差系数分别对珠江流域的西江、北江和东江年最大洪峰序列进行了变异诊断,并分析了变异点前后洪峰序列变化趋势。目前常从两个角度进行水文序列的非一致性分析,一是基于还原/还现将水文序列修正到过去状态或修正到现在状态,以保证序列的一致性;二是直接对水文序列进行频率分析[6]。
洪水遭遇可定义为各来源洪水的最显著特征量间的联合遭遇(如洪峰、洪量和持续时间等)[7],相对于分析实测洪水序列的实际遭遇情况,以显著特征量表征洪水序列在抓住所研究洪水特性的同时,能更灵活有效地使用联合分析方法。
本文以黄河和清水河为研究对象,选择洪峰流量为洪水显著特征量进行干支流洪水遭遇分析。对干支流洪水序列进行变异性诊断,采用混合分布拟合非一致性洪水序列,拟合年最大洪峰发生时间和量级分布;引入Archimedean Copula函数,构建黄河和清水河年最大洪峰发生时间和量级的联合分布,进而分析两河非一致性洪峰在发生时间和量级上的遭遇概率。
1 研究区概况
黄河宁夏段自中卫南长滩入境,流经卫宁灌区、青铜峡水库、青铜峡灌区,至石嘴山麻黄沟出境,区内流程397 km,分为峡谷段、库区段和平原段,区域水系分布如图1所示。入境洪水来自黄河上游流域降水。20世纪以来,发生洪峰流量超过6 000 m3/s的大洪水4次,分别为1904年、1946年、1964年和1981年,其中1904年和1946年对宁夏沿黄两岸造成严重洪灾,而1964年和1981年由于预报及时和采取了有效的防洪措施,很大程度上减少了洪灾损失。区间主要有清水河、红柳沟和苦水河3条支流汇入,其中对干流流量影响较大的是清水河,其流域面积达14 481 km2。清水河水系降水量为200~600 mm,由南向北递减;降水的年际变化大,最大相差3倍,年内分配也不均匀,多集中在7—9月。清水河多发暴雨洪水,且以局部暴雨为主,洪水过程一般持续3天,峰高量小,发生较大洪水的年份有1926年、1933年、1964年、1992年,其中1926年和1933年对下游造成较严重的洪水灾害,而1964年和1992年由于多座水库拦洪,使得下游并未发生洪灾。在实测资料中,黄河和清水河并未发生大洪水遭遇(1964年二者均发生较大洪水,洪峰发生时间却相差22 d),但不能因此忽略二者遭遇的可能性。目前青铜峡水库淤积日趋严重,防洪能力减弱,使下游两岸灌区的防洪形势更加严峻,而黄河和清水河洪峰是否遭遇对青铜峡水库入库洪峰流量影响很大,因此对两河洪峰遭遇情况进行分析显得尤为重要。
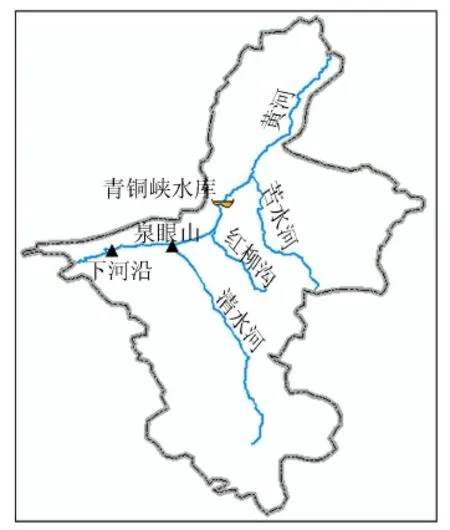
图1 黄河宁夏段水系示意图
2 研究方法
2.1 洪水序列非一致性分析
目前国内外对水文变异研究较多,Prohaska等[7-9]基于水文序列的确定性成分和随机性成分,以水文序列分布形式或分布参数发生显著变异为突变标准,提出了水文变异诊断的综合诊断系统。
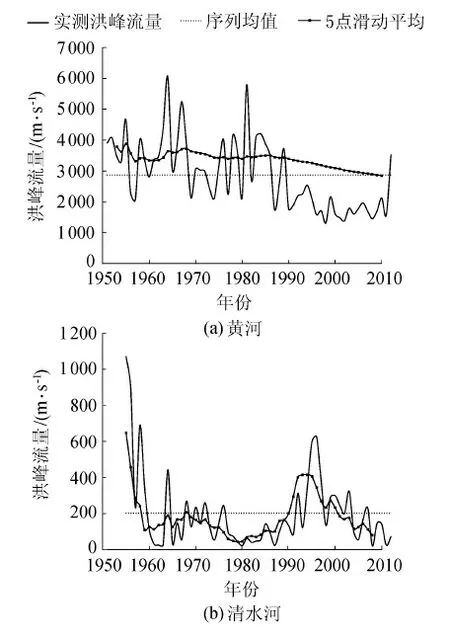
a. 初步诊断。绘制洪水序列的过程线和5点滑动平均线,观察序列的走势,进而用R/S法和极差分析法计算洪水序列的Hurst系数h,并根据表1(表中hα=0.661 和hβ=0.703分别为α=0.05和β=0.01时h的临界值)判断洪水序列的强弱程度。

表1 Hurst系数变异程度分级表[9]
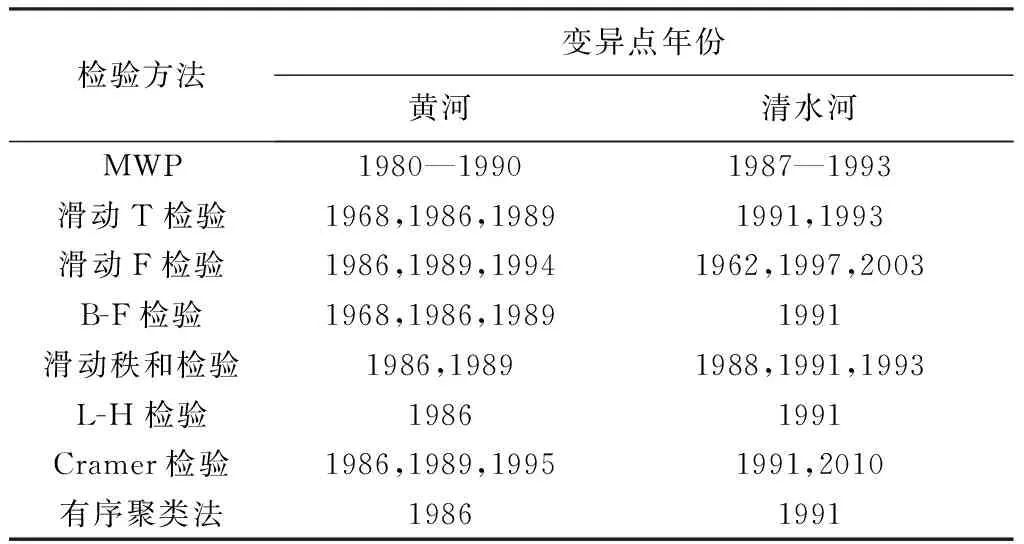
b. 详细诊断。采用下列较为成熟的8种检验方法从不同角度对初步诊断判定存在变异的序列进行详细诊断:MWP鉴定法[10]、滑动T检验法[11]、滑动F检验法、B-F检验法[12]、滑动秩和检验法[13]、L-H检验法、Cramer检验法[14]、有序聚类法[15]。由于不同检验方法假设前提和判断标准不一致,得到的检验结果往往存在一定差异。
c. 综合诊断。详细诊断是从数理统计角度找出可能的变异点,其结果不一定符合流域实际情况,还需结合物理成因分析,即下垫面变化、水利工程建设和水土保持工程等对水文序列的影响,对详细诊断结果进行合理性甄别,最终确定变异点。
2.2 洪峰分布形式确定
由于洪峰遭遇分为洪峰发生时间遭遇和洪峰量级遭遇,将洪峰序列分为洪峰发生时间序列和洪峰流量序列,分别构建洪峰发生时间分布和洪峰流量分布,基于变异诊断结果,对于存在变异的洪峰序列,采用多参数混合分布拟合。
2.2.1 洪峰发生时间分布
von Mises分布能很好地描述具有周期性或季节性的有限变量[16],选择von Mises分布对洪峰发生时间进行拟合,以汛期起始和结束时间为上下边界,将洪峰发生时间序列转换为[0,2π]圆周上的方向序列,转换公式为
(1)
式中:L为汛期长度;Di为洪峰发生时间。
von Mises分布概率密度函数为
(2)
式中:μ为位置参数,0≤μ≤2π;k为尺度参数,k≥0;I0(k)为0阶变形Bessel函数。
von Mises分布为圆周上的单峰分布,而洪峰时间序列通常呈多峰形态,单一分布函数往往不能准确描述序列分布形式,因此需要选择多个von Mises分布进行混合分布拟合,形式如下:
,
0≤μi≤2π,0≤ki)
(3)
式中:N为序列长度;αi为权重系数,满足α1+α2+…+αN=1。
采用改进似然比检验(MLRT)[18]对方向数据进行检验,确定其分布形态,构造统计量:
式中:n为数据个数;R和θ分别为方向数据对应的半径和角度。当n较大时,近似服从χ2分布。
由于von Mises分布的非正规性,通常情况矩估计不是渐进有效估计,极大似然估计得到结果并不是被估参数的相合估计,陈家骅等[17]对极大似然估计进行了改进。通过对比发现带惩罚的极大似然估计的结果最优,因此本文基于改进的期望最大(EM)算法采用带惩罚的极大似然估计进行混合von Mises分布参数估计。
2.2.2 洪峰流量分布
根据SL 44—2006《水利水电工程设计洪水计算规范》,选择P-Ⅲ型分布拟合洪峰流量序列,其密度函数形式如下:
(5)
式中ε、β和b0分别为形状、尺度和位置参数。
对于存在变异的洪峰序列,单一分布形式已不能准确拟合实际序列。成静清等[19]通过构建两个对数正态分布的混合分布对陕北实测平均流量序列进行拟合,得到比单一分布更好的成果。因此本文构建多分布形式混合分布对两河洪峰序列进行拟合,混合分布的密度函数形式为
(6)
式中:φi为权重系数;εi、βi和b0i为各分项密度函数参数。对混合分布参数,模拟退火算法是一种有效算法,然而传统模拟退火算法存在一些局限,如计算步长难确定,收敛速度慢,易漏掉最优解,为此众多学者进行了改进,朱颢东等[25]对退火过程和抽样过程进行了两阶段改进,并模拟得到比传统算法更优的解。因此,本文先用矩法进行参数初估计,再用模拟退火算法进行参数最终估计。
2.3 联合分布构建
Archimedean Copula函数族因其表达式简单和易于构造而被广泛应用,其中具有代表性的有Frank、Clayton和Gumbel函数。两河洪峰序列具有上尾相关性,且洪峰遭遇属于极值事件,Gumbel Copula函数能很好地满足以上特征,因此本文选择Gumbel Copula函数构建联合分布。两变量联合分布的表达式为
C(u1,u2)=exp{-[(-lnu1)θ+(-lnu2)θ]1/θ}
(7)
式中:u1和u2为边缘分布函数;θ为连接参数,θ>1。这里采用非参数法估计连接参数。
进行洪水遭遇分析时,通常将不同河流的洪峰流量视为不相关[20]或将同河流的洪峰发生时间和洪峰流量量级视为不相关[4],如此考虑固然能简化计算,但忽略了洪峰序列之间的部分相关性,使得计算结果不能准确反映洪峰遭遇特征。本文在综合考虑各河流洪峰序列自身内在的和彼此间相关性的基础上,构建洪峰序列四变量联合分布。由于每条河流洪峰发生时间序列和流量量级序列相关性较强,而河流之间的相关性较弱,相比于对称Copula函数,非对称Copula函数能更好地描述多变量之间的相关性,且对数据的拟合更灵活[21]。选择非对称构造中的半嵌套构造,其表达式为
C1(u1,u2)=exp{-[(-lnu1)θ1+(-lnu2)θ1]1/θ1}
(8)
C2(u3,u4)=exp{-[(-lnu3)θ2+(-lnu4)θ2]1/θ2}
(9)
C(u1,u2,u3,u4;θ1,θ2,θ3)=exp{-[(-lnC1)θ3+
(-lnC2)θ3]1/θ3}
(10)
式中:u1、u2、u3、u4为边缘分布函数;θ1、θ2、θ3为连接参数,且满足1<θ3<θ1,1<θ3<θ2。采用伪极大似然估计法[24]进行参数估计,用样本的经验分布函数代替边缘分布函数,则不需要进行边缘分布函数参数估计,从而有效避免边缘函数分布形式对相关参数估计结果的影响。
采用Gringorten公式计算经验联合频率:
(11)
式中:m为联合观测样本中满足(xj 选择非参数K-S检验法,对联合分布函数进行拟合检验,构造统计量: (12) 式中F0(x,y)为理论联合分布概率。 2.4 洪水遭遇风险分析 若两河洪峰不在同一天发生,洪峰流量无遭遇可言,因而,需先对洪峰发生时间遭遇进行分析,并以此为中间量进行洪峰流量遭遇分析。洪峰发生时间遭遇风险可定义为第i天同时发生洪水的概率: Pi=P(ti-1 (13) 式中T1和T2分别为两河洪水发生时间。 第i天两河同时发生指定量级洪峰(q1,q2)的概率为 P(i,q1,q2)=P(ti-1 Q1>q1,Q2>q2) (14) 式中Q1和Q2分别为两河发生的洪峰流量。 3.1 干支流洪峰序列非一致性分析 根据综合诊断法的思路对黄河和清水河洪峰序列进行变异性诊断,找出序列中最大可能变异年份。通过水文序列的合理性分析,已将清水河泉眼山站洪峰序列1955年、1956年数据作为历史特大值考虑,不参与变异性诊断。 a. 初步诊断。黄河和清水河年最大洪峰过程线及5点滑动平均线如图2所示。从图2可知,黄河年最大洪峰的5点滑动平均线在1986年后呈下降趋势;清水河年最大洪峰的5点滑动平均线在1993年前呈上升趋势,1993年后呈下降趋势。计算两河Hurst系数,黄河为0.858 7,属于强变异;清水河为0.807 7,属于中变异。初步诊断两河洪峰时间序列存在变异。 图2 黄河和清水河洪峰序列及5点滑动平均 b. 详细诊断。采用选定的8种检验方法对黄河和清水河洪峰序列进行检验,最有可能变异点见表2。由表2可知,每种检验法均检验出1986年为黄河序列可能变异点且在各可能变异点中占权重最大,1991年为清水河序列可能变异点且在各可能变异点中占权重最大,可以断定黄河在1986年发生变异,清水河在1991年发生变异。计算得黄河1986年前后和清水河1991年前后子序列的Hurst系数分别为0.527 4、0.541 3和0.616 2、0.587 3,均满足一致性要求。 表2 黄河和清水河变异点诊断结果 c. 综合诊断。黄河上游1986年龙羊峡水库和刘家峡水库实行联合调度,对上游天然径流进行拦蓄重分配,下游径流过程发生很大变化,洪峰流量削减尤为突出;20世纪80年代末至90年代初,对清水河流域水利工程进行清淤整治,使得水库群对洪峰的拦蓄调节能力显著增强,特别是对流域内经常发生的暴雨洪水有显著控制作用;20世纪80年代以来,随着大气平均温度升高,黄河上游和清水河流域地表蒸发量明显增大,汛期降水呈减少趋势,河道径流有变小趋势[22-23]。综合人类活动和气候变化因素分析,确定1986年为黄河年最大洪峰序列变异点,1991年为清水河年最大洪峰序列变异点。 3.2 干支流洪峰时间序列联合分布 图3 黄河和清水河洪峰发生时间概率密度拟合 基于特定EM算法,进行带惩罚的极大似然估计进行von Mises分布参数估计,结果见表3。根据已估计得到参数,确定两河时间序列TH和TQ的概率密度函数,并进行拟合,如图3所示,可以看出,TH和TQ的密度函数分别选择4峰和3峰混合分布均能很好拟合经验直方图。由密度函数确定分布函数,计算TH和TQ的理论概率,并与经验概率进行拟合,如图4所示,可以看出,TH和TQ的理论概率均能很好地拟合经验概率。 图4 黄河和清水河洪峰发生时间理论频率和经验频率拟合 河 流α1μ1k1α2μ2k2α3μ3k3α4μ4k4黄 河0.190.551.40.52.853.390.264.627.050.055.8826.04清水河0.041.5170.742.993.90.224.117.91 由相关性指标法计算得连接参数θ=1.034 3,联合分布函数为 式中:FTH(t)、FTQ(t)分别为TH和TQ的边缘分布。K-S检验法计算联合分布统计量D=0.068 4,小于临界值0.173,通过显著性检验,因此选择的联合分布是合理的。 3.3 干支流洪峰流量序列联合分布 根据洪峰序列非一致性检验结果,黄河和清水河洪峰量级序列各存在一个较强变异点,基于可靠性和易于计算原则,对原序列两部分进行混合分布拟合。由改进模拟退火算法进行参数估计,结果见表4。由式(5)确定两河洪峰量级分布函数,计算理论频率,与经验频率进行拟合,并用K-S检验法对拟合情况作检验,计算的黄河和清水河统计量D分别为0.076和0.126,均小于显著性水平0.182,构建的混合分布能较好地拟合黄河和清水河洪峰量级序列。 表4 黄河和清水河洪峰量级混合P-Ⅲ分布参数 构建干支流洪峰发生时间和量级的部分嵌套四维Gumbel Copula联合分布如下: C1(TH,QH)=exp{-[(-lnTH)θ1+(-lnQH)θ1]1/θ1} (16) C2(TQ,QQ)=exp{-[(-lnTQ)θ2+(-lnQQ)θ2]1/θ2} (17) C(TH,QH,TQ,QQ;θ1,θ2,θ3)=exp{-[(-lnC1)θ3+ (-lnC2)θ3]1/θ3} (18) 用伪极大似然法估计联合分布参数,连接参数为θ1=1.246,θ2=1.115,θ3=1.065。首先分别对C1和C2进行拟合检验,用式(13)(14)计算黄河和清水河各自洪峰发生时间和量级的两变量理论联合频率和经验联合频率并进行拟合;进一步计算C1和C2的K-S统计量D1=0.051和D2=0.054,均小于临界值0.173,通过显著性检验。对C进行拟合检验,其K-S统计量D=0.083,小于临界值0.178,通过显著性检验。这表明上面基于Gumbel Copula构建的部分嵌套联合分布函数能很好地拟合黄河和清水河洪峰发生时间和量级。 表6 两河不同频率洪峰遭遇概率峰值和对应的遭遇流量 3.4 洪水遭遇风险分析 式(10)计算的黄河和清水河洪峰在每一天遭遇的概率如图5(a)所示。由图5(a)可以看出,6月15日之前,二者遭遇的概率几乎为零;7月15日至8月15日为二者主要遭遇时段,也是黄河和清水河洪峰出现的主要时段,在7月31日二者遭遇的概率的达到最大,为3.36×10-4;8月18日至8月31日遭遇概率逐渐增大,并在8月31日出现第二峰值1.15×10-4,主要是由于黄河汛期较长,除7月中下旬至8月上旬的主汛期外,还存在8月末至9月初的次主汛期,而清水河汛期相对滞后于黄河,使得二者在8月25日至9月5日出现第二次遭遇概率高峰。 式(11)计算的同频率洪峰在每天遭遇的概率如图5(b)所示,为便于对比,已将概率值作负对数处理。从图5(b)可以看出,两河同频率洪峰在7月28日和9月2日附近出现两个遭遇高峰,表5列出6种重现期同频率洪峰遭遇的两个概率峰值;汛初和汛末洪峰遭遇概率相对很小,与黄河和清水河年最大洪峰极少出现在汛初和汛末的实际情况相符。表6为两河不同频率洪峰遭遇概率峰值及对应的洪峰流量(即青铜峡水库入库洪峰流量)。根据可能发生遭遇的联合洪峰流量,结合青铜峡水库调度规则,提前预留足够防洪库容,以保证能进行有效拦洪削峰。从表6可以看出,黄河和清水河十年一遇洪峰遭遇的概率为650.91×10-8,未达到万分之一,且在58 a的实际监测中两河十年一遇洪峰也未发生遭遇,因此,对下游防洪要求较低的工程,可以忽略二者的遭遇风险。 图5 黄河和清水河洪峰遭遇概率 表5 同频率洪峰遭遇概率峰值 a. 由于气候、环境变化和人类活动影响,黄河洪水序列和清水河洪水序列发生显著变化的时间不一致,经三阶段诊断,表明两河洪水序列发生显著变异的年份分别为1986年和1991年。 b. 不考虑洪峰量级情况下,黄河与清水河洪水发生时间出现遭遇的概率分别在7月31日和8月31日达到峰值,概率值分别为3.36×10-4和1.15×10-4。 c. 黄河与清水河同频率洪峰遭遇概率分别在7月28日和9月2日达到两个峰值;两河不同频率洪峰遭遇概率在7月26日至8月2日和8月31至9月5日两个时段内达到峰值。洪峰遭遇概率均小于万分之一,因此在实际工程中可以忽略遭遇风险。 [ 1 ] SALVADORI G,MICHELE C D.On the use of Copulas in hydrology: theory and practice[J].Journal of Hydrologic Engineering,2007,12(4):369-380. [ 2 ] YAN B W.Coincidence probability of precipitation for the middle route of South-To-North Water Transfer Project in China[J].Journal of Hydrology,2013,499:19-26. [ 3 ] GENEST C,FAVRE A C.Meta-elliptical Copulas and their use in frequency analysis of multivariate hydrological data[J].Water Resource Research,2007,43:1-12. [ 4 ] CHEN L,SINGH V P.Flood coincidence risk analysis using multivariate Copula functions[J].Journal of Hydrologic Engineering,2012,17(6):742-755. [ 5 ] ZHANG Q,GU X H.Flood frequency analysis with consideration of hydrological alterations: changing properties,causes and implications[J].Journal of Hydrology,2014,519:803-813. [ 6 ] ALILA Y,MTIRAOUI A.Implications of heterogeneous flood-frequency distributions on traditional stream-discharge prediction techniques[J].Hydrological Processes,2002,16(5):1065-1084. [ 7 ] PROHASKA S,ILIC A.Multiple-coincidence of flood waves on the main river and its tributaries[J].IOP Conference Series: Earth and Environmental Science,2008,4:1-8. [ 8 ] 谢平,陈广才,夏军.变化环境下基于趋势分析的水资源评价方法[J].水力发电学报,2009,28(2):14-19.(XIE Ping,CHEN Guangcai,XIA Jun.The assessment method of water resources based on trend analysis of changing environments[J].Journal of Hydroelectric Engineering,2009,28(2):14-19.(in Chinese)) [ 9 ] 谢平,雷红富,陈广才,等.水文变异诊断系统[J].水力发电学报,2010,29(1).85-90.(XIE Ping,LEI Fuhong,CHEN Guangcai,et al.Hydrological alteration diagnosis system[J].Journal of Hydroelectric Engineering,2010,29(1):85-90.(in Chinese)) [10] PETTIT A N.A nonparametric approach to the change point problem[J].Applied Statistic 1979,28:126-135. [11] PATRICK D B,SHLOMO S S.Increasing physicians awareness of impact of statistics on research outcome: comparative power of thet-test and Wilcoxon Rank-Sum test in small samples applied research[J].Journal of Clinical Epidemiology,1999,52(3):229-253. [12] BROWN M B.FORSYTHE A B.The small sample behavior of some statistics which test the equality of several means[J].Techno Metrics,1974,16(1):129-132.[13] 谢平,陈广才,雷红富,等.变化环境下地表水资源评价方法[M].北京:科学出版社,2009. [14] 李瑞雪,张明军,金爽,等.乌鲁木齐河流域气候变化的区域差异特征及突变分析[J].干旱区地理,2010,33(2):243-250.(LI Ruixue,ZHANG Mingjun,JIN Shuang,et al.Regional difference and catastrophe of climate change over Urumqi River Basin[J].Arid Land Geography,2010,33(2):243-250.(in Chinese)) [15] BRUNSDO C,CORCORAN J.Using circular statistics to analyze time patterns in crime incidence[J].Computers,Environment and Urban Systems,2006,30:300-319. [16] FU Y J.Modified likelihood ratio test for homogeneity in a mixture of von Mises distributions[J].Journal of Statistical Planning and Inference,2008,138:667-681. [17] 陈家骅,李鹏飞,谭鲜明.混合von Mises模型的参数估计[J].系统科学与数学,2007,27(1):59-67.(CHEN Jiahua,LI Pengfei,TAN Xianming.Inference for von Mises Mixture in mean direction and concentration parameters[J].Journal of System Science and Mathematical Science,2007,27(1): 59-67.(in Chinese)) [18] CALDERARA S,PRATI A.Mixtures of von Mises distributions for people trajectory shape analysis[J].Transactions on Circuits and Systems for Video Technology,2011,21(4):457-471. [19] 成静清,宋松柏.基于混合分布非一致性年径流序列频率参数的计算[J].西北农林科技大学(自然科学版),2010,38(2);229-234.(CHENG Jingqing,SONG Songbai.Calculation of hsdrological frequency parameters of inconsistent annual runoff series based on mixed distribution[J].Journal of Northwest Agriculture and Forestry University(Science and Technology),2010,38(2):229-234.(in Chinese)) [20] 闫宝伟,郭生练,陈璐,等.长江和清江洪水遭遇风险分析[J].水利学报,2010,41(5):553-559.(YAN Baowei,GUO Shenglian,CHEN Lu,et al.Flood encountering risk analysis for the Yangtze River and Qing River[J].Journal of Hydraulic Engineering,2010,41(5):553-559.(in Chinese)) [21] LIEBSCHER E.Construction of asymmetric multivariate copulas[J].Journal of Multivariate Analysis,2008,99:2234-2250. [22] 徐宗学,张楠.黄河流域近50年降水变化趋势分析[J].地理研究,2006,25(1):27-34.(XU Zongxue,ZHANG Nan.Long term trend of precipitation in the Yellow River Basin during the past 50 years[J].Geographical Research,2006,25(1):27-34.(in Chinese)) [23] 时兴合,秦宁生,汪青春,等.黄河上游径流变化特征及其影响因素初步分析[J].中国沙漠,2007,27(4):690-697.(SHI Hexing,QIN Ningsheng,WANG Qingchun,et al.Analysis on runoff variation characteristics and influencing factors in the upper Yellow River[J].Journal of Desert Research,2007,27(4):690-697.(in Chinese)) [24] GENEST C,GHOUDI K,RIVEST L P.A semi-parametric estimation procedure of dependence parameters in multivariate families of distributions[J].Biometrika,1995,85(3):543-552. [25] 朱颢东,钟勇.一种改进的模拟退火算法[J].计算机技术与发展,2009,19(6):32-35.(ZHU Haodong,ZHONG Yong.A kind of renewed simulated annealing algorithm[J].Computer Technology and Development,2009,19(6):32-35.(in Chinese)) Coincidence risk analysis for non-stationary flood peak of Yellow River and its tributaries in Ningxia Hui Autonomous Region //LI Ziyuan, FENG Ping, YUAN Ximin (StateKeyLaboratoryofHydraulicEngineeringSimulationandSafety,TianjinUniversity,Tianjin300072,China) The coincidence risk of the non-stationary flood peak between the Yellow River and Qingshui River was analyzed. The variability of flood peak time series was detected using the comprehensive diagnosis method. The mixed Von Mises distribution and mixed P-Ⅲ distribution were used to fit the flood occurrence dates and peak magnitudes, respectively. The asymmetric partially nested Archimedean Copula function was selected to establish the joint distribution of flood peaks of the two rivers, and the occurrence dates and corresponding magnitudes between the two rivers were studied. Diagrams of coincidence risk of floods with different combinations of frequencies of the two rivers were provided. The results indicate that the flood time series in both rivers had changed; the coincidence risk of the flood peak occurrence dates of the two rivers peaked on July 31 and August 31, with values of 3.36×10-4and 1.15×10-4, respectively; and the peak coincidence risks of flood peaks with difference frequencies were obtained in two periods, from July 26 to August 2 and from August 31 to September 5. flood peak coincidence; non-stationary; mixed distribution; Copula function; risk analysis; Yellow River; Qingshui River 10.3880/j.issn.1006-7647.2016.06.010 国家自然科学基金(51179117,51209157) 李子远(1991—),男,硕士研究生,主要从事水文及水资源研究。E-mail: 362919252@qq.com TV122+.5 A 1006-7647(2016)06-0051-07 2015-10-10 编辑:郑孝宇)3 应用分析
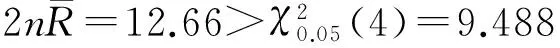



4 结 论
