开放海域污染物扩散的分形模拟
2016-12-08爱迪生保尔董艳梅
瞿 波,爱迪生·保尔, 董艳梅
(1.南通大学理学院,江苏 南通 226007; 2.英国卡迪欧数值公司,英国 爱丁堡 EH33 1EH;3.昆明理工大学城市学院,云南 昆明 650051)
开放海域污染物扩散的分形模拟
瞿 波,爱迪生·保尔2, 董艳梅3
(1.南通大学理学院,江苏 南通 226007; 2.英国卡迪欧数值公司,英国 爱丁堡 EH33 1EH;3.昆明理工大学城市学院,云南 昆明 650051)
通过对传统分数布朗运动模型以及改进了的FBMINC模型的分析,与粒子跟踪模型结合,提出应用范围更广的加速分数布朗运动(AFBM)粒子跟踪模型,并用于模拟海洋表面漂浮污染团的扩散。模拟结果表明,与传统模型的模拟结果比较,加速分数布朗运动粒子跟踪模型更准确可靠;由于豪斯特指数的取值范围得到扩展,加速分数布朗运动粒子跟踪模型的应用范围更广泛。
扩散;加速分数布朗运动;粒子追踪模型;分形;开放海域
研究海洋表面的浮标轨迹及污染物的扩散方法有很多,如苏京志等[1]建立了以海表地转流为主要回归自变量的回归模型来模拟浮标漂流轨迹;郭民权等[2]在Daniel 等[3]提供的方法的基础上,通过追踪海表漂移物轨迹和目标大小,用拉格朗日算法,建立了海表目标物漂移的预测模型,用树枝模拟的方法研究了浮子漂移在平潭近岸海域的轨迹;王胜正等[4]结合海表目标漂移物的形状和统计模型,模拟了海表漂移物的轨迹。海表漂浮污染物的传播和风速有关;陈丽萍等[5]发现,随着风速的增大,水气交界面附近的速度梯度会增大,从而增大挥发性污染团的挥发;韩龙喜等[6]在研究连云港近岸海域污染物随潮流输移和浓度增量的变化规律时,采用了二维数学模型模拟研究海域的流场和污染物输移轨迹,发现污染物的浓度增量与污染物的排放量成正比,与水体流速、流量成反比;武国正等[7]研究了分形维数算法在水体营养状况评价中的适用性。本文用分形中的分数布朗运动来研究流体中污染物的传播。
由于更适合对普遍的、各种不同程度扩散的模拟[8-10],分数布朗运动已经越来越受到人们的青睐。Qu等[11]研究了分数布朗运动的FBMINC 模型, 并与Mandelbrot的分数布朗运动模型(FBM)进行比较, 得出比FBM更精准的结果。瞿波等[12]用FBMINC模型模拟了沿海海表面污染物的扩散,并与传统的布朗运动进行了比较,发现控制扩散程度的豪斯特指数H(0
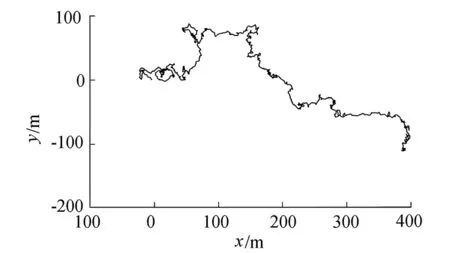
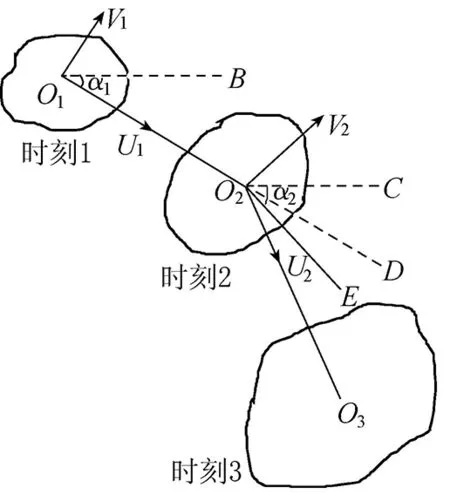
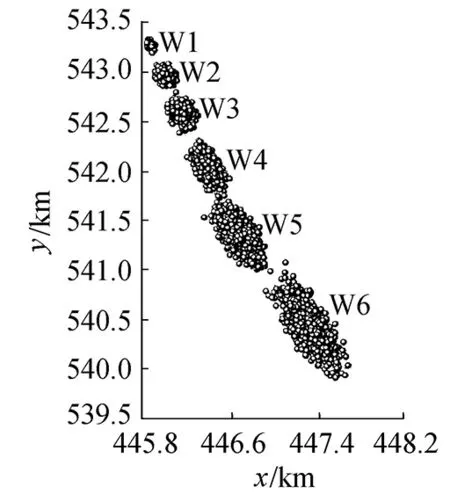
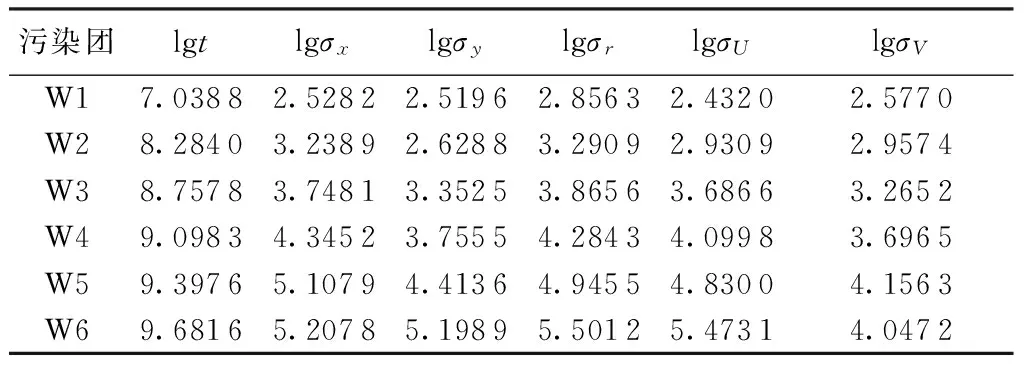
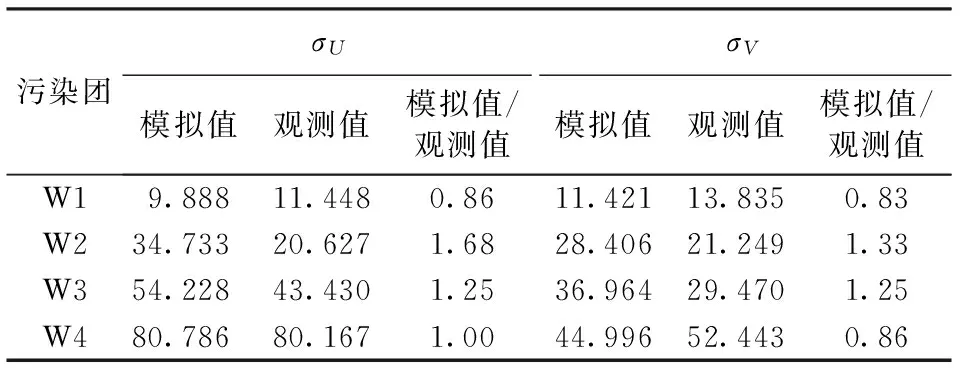
分数布朗运动因其灵活性,不仅被应用于流体中[16], 而且被应用于日常生活的很多分支, 包括金融、股市、医疗器械(脑电图)、人体的毛细胞血管分布、岩石的裂缝等。而分数布朗运动粒子追踪模型在沿海、河流等区域有广泛的应用。对宽阔的海面,分数布朗运动中的豪斯特指数的限制(0 Mandelbrot的分数布朗运动模型[17]为 (1) 式中:BH(t)为具有豪斯特指数H的分数布朗运动在时刻t的轨迹;B(s)为布朗运动在时刻s的轨迹;Γ(x)为伽玛函数。 式(1)中的时间是从负无穷大开始的。如果限制时间从零点开始, 得到改进了的分数布朗运动模型: (2) 瞿波等[11-12]对FBM作了改进,得到FBMINC模型: (i-j-1)H-1/2]R(j)+R(j-1)} (3) 式中:i为时间;M为记忆长度;R为随机漫步。 FBMINC模型克服了FBM模型的一些弱点,变得更精准[11],已成功应用于海湾和河流扩散模拟中[9,12,16]。 一簇污染物随时间扩散的方差和时间t的关系为 (5) 式中σc(t)为标准差。 Sanderson等[14]发现海洋表面浮标的轨迹大多呈分数布朗运动,其豪斯特指数在0.73~0.84之间。海洋上的浮标分数维数可用结构散布技术计算[18]。 图1是一个海上浮标的轨迹[18],其豪斯特指数是0.8。但是在宽阔的海面上,豪斯特指数可以超过1[14-15],需要新的方法来模拟这种情形的轨迹。 图1 海上浮标的移动轨迹[15] (6) 式中β为常数,β≥ 0。如果β=0, 将变成分数布朗运动(式(5))。因此,加速分数布朗运动可以通过对时间的调整由分数布朗运动得到。 设基于分数布朗运动所需要的时间是t, 要成为加速分数布朗运动,所需要调整的时间为t′=tγ, 这里γ>1。根据原来的分数布朗运动有 (7) 式中Xp为加速分数布朗运动在时间t的轨迹。由于Xp(t)的方差满足Var(Xp(t))∝t′2H,有 t′2H=(tγ)2H=t2H+β (8) (9) 所以,在加速分数布朗运动模型中,时间步长、记忆M和时间间隔Δt都需根据式(9)重新调整。 可以用lgσc-lgt图中的斜率来计算豪斯特指数[16, 18]。 当运动是加速分数布朗运动时,lgσc-lgt的斜率不再限于1以内,此时用Hη来表示此斜率,并称之为表面豪斯特指数。 假设 lgσc-lgt曲线的斜率为Hη,则2H+β=2Hη,从而有 β=2(Hη-H) (10) 因此, 对加速分数布朗运动模型, 一组粒子扩散时的标准差ση和时间的关系式如下: ση=(2Dft)Hη (11) 式中Df为扩散系数。两边取对数, 得: lgση=Hηlgt+Hηlg(2Df) (12) 这里, lgση-lgt曲线的斜率即为表面豪斯特指数Hη,其值可以大于1, 截距是 A=Hηlg(2Df) (13) 可得Df=0.5×10A/Hη (14) (15) 将式(9)代入可得: (16) 由此就可以模拟污染物在加速分数布朗运动时的轨迹。一般的水利工程中,扩散系数在0.01~0.02之间[16]。对海面上漂浮的污染物轨迹来说,可以取H=0.8,Df=0.01,然后计算出表面豪斯特指数Hη。此时Hη>1。 流体中污染团的传播轨迹由分流和扩散两个运动的组合来完成,其位置变化为: Δxi=U(xi,yi)Δt+ΔBHx(xi,yi) (17) Δyi=V(xi,yi)Δt+ΔBHy(xi,yi) (18) 式中:Δxi、Δyi分别为污染团在两个坐标方向上的位置变化;U(xi,yi)、V(xi,yi)为在时刻t沿两个相互垂直方向上的水流速度;ΔBHx(xi,yi)、ΔBHy(xi,yi)为在U、V方向上的扩散位移, 可由分数布朗运动FBMINC模型计算得到。在宽阔的海面上模拟污染团的扩散,将会用到加速分数布朗运动。图2为海面上漂浮的一个污染团在3个时刻的形状和位置(图中O1B和O2C分别代表时刻1和时刻2的x方向,O2D代表时刻1至时刻2污染团的扩散方向,O2E代表时刻2流速方向的垂直方向)。 图2 沿扩散方向的运动 英国诺森伯兰海洋所在1995—1996年在英国诺森伯兰海洋投放了几个燃料污染团, 英国沃灵夫特水利公司(HRWallingford,HR)用传统的布朗运动模型对此做了模拟,笔者用加速分数布朗运动粒子扩散模型对相同的数据也进行了模拟,结果表明笔者的模拟略胜英国沃灵夫特水利公司的模拟[16]。 图3是对在英国诺森伯兰海洋Horden 区域的污染物W (W1, W2, W3, W4, W5, W6代表污染物扩散的不同时刻的等高图)的模拟结果。本文用一簇2 000个粒子组成的粒子云(P=2 000)来模拟一个污染物体。每个粒子都遵循式(17)(18)描述的运动轨迹(分流加分散,而分散部分用了加速分数布朗运动)。对此粒子云,可以计算出平面的等高线,而每个时刻的质量浓度由外而内分别为0.01 μg/L、0.1 μg/L、1 μg/L、 10 μg/L、 100 μg/L。 当等高线图扩散开去时,最大的质量浓度从100 μg/L降低到10 μg/L,或甚至1 μg/L。先计算出沿x、y、r(x,y是坐标轴方向,r是沿漩涡半径的方向)、U、V方向上的粒子束扩散运动的标准差(σx,σy,σr,σU,σV)。表1是沿这5个方向标准差的计算结果。 根据式(12), 可以计算出5个方向表面豪斯特指数Hη分别为1.065 4、1.090 4、1.081 6、1.232 6、0.683 3,可见,对污染物W,Hη的值在0.383 3~1.232 6之间,有4个方向的Hη都超过了1。 图3 FBMINC模型的粒子云扩散轨迹 对模拟结果和原始观测数据以及英国Wollingford水利公司的模拟结果作了比较,比较的方法用了两种:一种是比较标准差,另一种是比较浓度的水平轮廓面积的大小。结果表明,标准差的比较是最稳定的方法。沿U,V方向的标准差的计算公式如下: 表1 污染团扩散过程的lgt 和lgσ (19) (20) 表2为污染团W的模拟结果在U、V方向上的不同时刻污染物扩散的标准差和相应的观测值的比较,结果显示,模拟结果和观测值的差距不大。模拟的结果在W1和W4低于观测值,而在W2、W3 高于观测值,相对误差在±30%之内。因为W5、W6这两个时刻的最大质量浓度小于1 μg/L,本身的精确度不高,忽略而不作比较。 表2 U、 V方向模拟结果和观测值的比较 对其他的污染物也作了比较,结果显示,模拟和观测结果的标准差之比在0.4~1.85之间。考虑到在整个计算过程中始终选用了同一个H值(H=0.8),在此基础上再计算表面豪斯特指数的值,因此认为结果较为满意。此外与HR的模拟面积以及观察面积比较[16-17], 结果表明,HR的模拟结果低估了通常的浓度水平,而本文的模拟结果高估了低浓度的水平。 本文在以往的分数布朗运动的基础上,介绍了加速分数布朗运动模型的粒子追踪模型,并利用AFBM粒子追踪模型进行模拟。根据英国森伯兰海洋所提供的污染团随时间扩散的水平面等高线图, 将其转化成网格点数据,然后计算粒子束运动的标准差。对AFBM模型作了推导,主要思路是在FBMINC模型的基础上,通过调节时间参数,从而调节豪斯特指数和扩散系数, 以达到加速运动的目的。本文用AFBM粒子跟踪模型对2 000个粒子云进行扩散追踪,计算出粒子云的标准差,并和实际数据(等高图)进行了比较。模拟的结果和观测值的差距不大。尽管本文的模拟结果高估了低浓度的水平, 而HR的模拟结果低估了通常的浓度水平,总的来说,本文的模拟效果略胜一筹。 加速分数布朗运动粒子跟踪模型的表面豪斯特指数Hη具有更大的变化范围(Hη可以大于1),显示出在模拟开阔海面污染物扩散方面的优越性。本文介绍的方法方便简捷、实用,并可以推广到三维的情形。 [ 1 ] 苏京志,王东晓,陈举,等.利用回归模型模拟卫星跟踪海洋漂流浮标轨迹[J].地球科学进展,2005,20(6): 607-617.(SU Jingzhi,WANG Dongxiao,CHENG Ju,et al.Modeling the trajectories of satellite tracked drifters with regression models[J].Advances in Earth Science,2005,20(6): 607-617.(in Chinese)). [ 2 ] 郭民权,曾银东,李雪丁,等.平潭近岸海域浮子漂移轨迹及其数值模拟[J].应用海洋学学报,2014,33(4): 449-454.(GUO Minquan,ZENG Yindong,LI Xueding,et al.Buoy drift trajectory and numerical simulation in Pingtan coastal waters[J].Journal of Applied Oceanography,2014,33(4): 449-454.(in Chinese)). [ 3 ] DANIEL P,JAN G,CABIOC H F,et al.Drift modeling of cargo containers[J].Spill Science & Technology Bulletin,2002,7(5/6): 279-288. [ 4 ] WANG Shengzheng,NIE Haobin,SHI Chaojian.A drifting trajectory prediction model based on object shape and stochastic motion features[J].Journal of Hydrodynamics,2014,26(6): 951-959. [ 5 ] 陈丽萍,程璟涛,蒋军成,等.风速引起的湍流对挥发性污染物传质的影响[J].河海大学学报 (自然科学版),2012,40(6):610-614.(CHEN Liping,CHENG Jingtao,JIANG Juncheng,et al.Effect of turbulence induced by wind velocity on volatile pollutants mass transfer[J].Journal of Hohai University (Natural Sciences),2012,40(6): 610-614.(in Chinese)) [ 6 ] 韩龙喜,易路,刘军英,等.连云港近岸海域污染物输移规律[J].河海大学学报(自然科学版),2011,39(3): 248-253.(HAN Longxi,YI lu,LIU Junying,et al.Transport laws for pollutants in coastal area of Lianyungang City[J].Journal of Hohai University (Natural Sciences),2011,39(3): 248-253.(in Chinese))[ 7 ] 武国正,徐宗学,李畅游.基于分形理论的水体富营养状况评价及其验证[J].水资源保护,2012,28(4): 12-16.(WU Guozheng,XU Zongxue,LI Changyou.Water eutrophication assessment and validation based on fractal theory[J].Water Resources Protection,2012,28(4): 12-16.(in Chinese)) [ 8 ] OSBORNE A R,KIRWAN A D,PROVENZALE A,et al.Fractal drifter trajectories in the Kuroshio extension[J].Tellus,2010,41A(5): 416-435. [ 9 ] QU B,ADDISON P S.Modelling flow trajectories using fractional Brownian motion[EB/OL].(2015-10-24) https://www.computer.org/web/csdl/index/-/csdl/proceedings/iwcfta/2010/4247/00/4247a420-abs.html [10] LI M.On the long-range dependence of fractional Brownian motion,mathematical problems in engineering[M].New York.:Hindawi Publishing Corporation,2013. [11] QU B,ADDISON P S.Development of FBMINC model for particle diffusion in fluids[J].International Journal of Sediment Research,2009,24(4): 439-454. [12] 瞿波,保尔·爱迪生.流体中污染物扩散的分形模拟[J].水利水电科技进展,2009,29(6): 9-12.(QU B,ADDISON P S.Simulation of fractal pollutant dispersion in fluids[J].Advances in Science and Technology of Water Resauces,2009,29 (6): 9-12.(in Chinese)) [13] SANDERSON B G,PAL B K.Patch diffusion computed from Lagrangian data,with application to the Atlantic equatorial undercurrent[J].Atmosphere-Ocean,1990,28(4): 444-465. [14] SANDERSON B G,GOULDING A.The fractal dimension of relative Lagrangian motion[J].Tellus,1990,42(5).Part 6: 550-556. [15] SANDERSON B G,BOOTH D A.The fractal dimension of drifter trajectories and estimates of horizontal eddy-diffusivity[J].Tellus,1991,43(5): 334-349. [16] 瞿波.分形几何与流体[M].上海:上海社会科学院出版社,2016. [17] MANDELBROT B B,van NESS J W.Fractional Brownian Motions,fractal noises and Applications[J].SIAM Review,1968,10(4): 422-437. [18] ADDISON P S.Fractals and chaos: an illustrated course[M].London: Institute of Physics Publishing.1997. Fractal simulation of diffusion of pollutants in open ocean //QU Bo1, ADDISON Paul S2, DONG Yanmei3 (1.ScienceFaculty,NantongUniversity,Nantong226007,China; 2.CardioDigitalLtd.,EdinburghEH33 1EH,UK; 3.CityCollegeofKunmingUniversityofScienceandTechnology,Kunming650051,China) The traditional fractional Brownian motion (FBM) model and the improved FBMINC model were analyzed. Based on these two models and the particle tracking model, an accelerated fractional Brownian motion (AFBM) particle tracking model was developed and used to simulate the diffusion of floating pollutants in oceans. The simulation results show that, compared with the traditional model, the AFBM particle tracking model is more reliable and has a wider scope of application, due to the wider range of the Hurst exponent. diffusion; accelerated fractional Brownian motion; particle tracking model; fractal; open ocean 10.3880/j.issn.1006-7647.2016.06.004 国家自然科学基金 (41276097) 瞿波(1962—),女,副教授,博士,主要从事分形和环境数学模型研究。E-mail:qubo@ntu.edu.cn O29 A 1006-7647(2016)06-0020-04 2015-10-24 编辑:郑孝宇)1 分数布朗运动模型
2 加速分数布朗运动模型
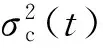
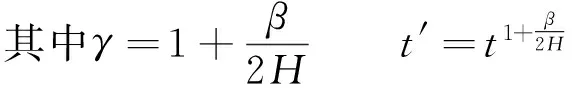



3 加速分数布朗运动的粒子跟踪模型
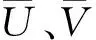
4 结 语
