初中数学教学中数形结合思想的实践探讨
2016-12-08赵敏杰
赵敏杰
(长春市九台区西营城中心学校 吉林长春 130524)
初中数学教学中数形结合思想的实践探讨
赵敏杰
(长春市九台区西营城中心学校 吉林长春 130524)
随着时代的飞速发展,教育事业也在不断提高与改进,而初中教育越来越起到关键作用,数学作为教育中的一门主要学科,也越发显得关键,自改革开放以来,我国关于中小学教育越来越重要,而数学这门学科,更是重中之重。如何提高学生们的学习效率成为了关键。
初中数学 数形结合 教学
一、数学教学
初中数学,是链接我们中小学的重要桥梁,锻炼着我们的理性思维,是我们从幼稚走向成熟的关键。初中时期也正是一个人的身体,思维,思想走向成熟的过程,而数形结合又是初中教育中一个不可缺少的点,本文以初中教学与数形结合思想为研究对象,以提高学生们的思维能力,学习质量为目标,来对初中数学教学与数形结合思想的实践探讨 。[1]
二、论初中数学与数形结合的重要性
目前大多数中学在数学教学中往往只重视课本上的理论知识的传授,却忽略和理论与实际的差距,以至于等到他们上高中时,正式接触到数形结合,把理论与现实接轨是成绩的急速下滑。在初中就摄入数形结合思想对初中数学方面的教学而言是极为有效的,其将抽象的数学知识转化为图形特性,“以形助数”“以数辅形”,发展学生思维,培养学生数形结合意识与理性分析能力,可提高学生分析问题、解决问题的能力,从而更有利于初中生对数学知识的理解和掌握。[2]
对于老师来讲,可以说,数形结合对于初中教学,对于发展学生们的理性思维有不可替代的作用,通过对于图形的直观分析,把数字运算能力与图形相结合,帮助学生们更好地掌握需要学习的内容。在我们的生活中,有许多都需要用到数形结合,例如,建一栋房子,你不能什么都不做就去建房,需要计算,画图等等。
三、数形结合思想在初中教学中的应用
数与形结合是数学解题中常用的思考方法,数形结合的思想可以使得抽象化的数学问题直观具体的用图形的形式表现出来,把枯燥的数学生动化、形象化,勾起学生们对数学的兴趣,从而达到更好的教学目标。
在步入初中阶段前,大多学生已经掌握了一定的图形知识,并且能够对一些学习工具熟练应用,例如直尺、量角器、三角板、圆规等。而在初中数学教学过程中,很多方面用数形结合来讲解,能解决学生们的很多难以理解的问题,就如函数、方程、以及一些直观数量的表达等。
①函数与图形间的结合。在初中教学中函数对于我们是非常有用的,它始于初中,对于这门几乎贯彻我们一生学习生涯都不可缺少的内容,打好基础非常关键,学好它却要下大功夫,如何直观形象的了解它,对学好函数很重要。而把抽象的函数用图形来表示出了,达到数与形的有效结合,把知识化繁为简,让学生达到一个有效吸收。
初中教学中,一次元函数还相对简单,但二次元函数却仿佛一下遇到了瓶颈,抽象的知识让学生云里雾绕,一些摸不到窍门的学生仿若遇到天敌,再努力也学不好,因此,在教学中,针对函数与图形间的紧密联系,教师们选用了教会学生通过图形来对函数直观地了解,找准问题关键,达到学好函数的目的。
例如:在二次元函数y=ax2+bx+c中,已知数有(1,y1)、(2,y2)、(-4,y3),在函数中,判断y1、y2、y3的大小。
这样的判断题学生若是在求解过程中,把数值依次带入求解是一种常规方法,但这样会增加学生们的计算量与解题时间,有时慌张还有可能出错,但如果学生们掌握了数形结合,把图形画出来,就会很容易比较出三个未知数的大小,方便,快捷。
②用图形来对一些数字的直观表达
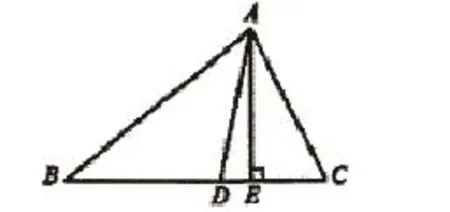
图1
此题可如此分析,三角形三角之和为180度
2∠BAD+∠B+∠C=180° ∠BAD=40°
∠DAE=180°-∠AED-∠ADE
∠ADE=∠B+∠BAD=80° ∠DAE=10°
看图解答,非常好理解。
③方程运算与图形相结和
在初中,我们学习的方程有好几种,一元一次方程、二元一次方程、一元二次方程等,下面就用一个初中教学课程中的实际应用题来做例子论证一下方程与图形结合的思想吧!
小明去上学的路上有一株很高的树,再一次上完学回到家之后,他突然好奇树的高度究竟有多高?于是他就用刚刚学到的知识进行了一次数与形,结合实际求出了树的精确高度。
在第二天的上午10点,它用一根较小的木棍立于地上,用尺子测量出了木棍与影子的高度,之后他又用几种不同高度的木棍进行了测量,并以等比例画在了纸上,结果发现在不同的比例下,他们的图形出奇的一致,也就是说在同一时间,木棍与影子间的比例成正比。于是小明测量出大树影子的长度,算出了大树的具体高度。
我国著名数学家华罗庚说过:“数形结合百般好,隔裂分家万事休”就说明了“数”与“形”的特点,它反映了事物的两个方面属性,却又相互依存不可分割。
结语
在初中教学中,将数形结合运用到教学中,是一种非常有效的方法,将数形结合的概念传递给学生,培养学生对于数量与几何间相互联系的条件反射,从而达到学生们对于数学的理性思考能力与灵活运用,达到教师们的教学目的。
[1]侯曙光. 数形结合思想在初中数学教学中的渗透探究[J]. 新课程学习·中旬, 2013(11):53-55.
[2]邓建华. 初中数学教学中数形结合思想的应用[J]. 数理化解题研究:初中版, 2015(19):32-32.
赵敏杰(1966.11-)女,长春市九台区西营城中心学校,教师。
