直击中考题寻宝大揭秘

谢　燕

直击中考题寻宝大揭秘

谢燕

中考是对同学们三年初中学习的大检阅，一道道中考题既是同学们要攀登和战胜的一座座山峰，也是我们学习的一座座宝藏，让我们一起通过中考题来探寻学习和解题的奥秘吧！

例1（2016·江苏南京）如图1，AB、CD相交于点O，OC=2，OD=3，AC∥BD.EF是△ODB的中位线，且EF=2，则AC的长为.

图1

本题是三角形的中位线和三角形相似的小综合题，只要牢固掌握基本图形、基本知识就可迎刃而解.运用相似求线段长度是中考中常见的题型.

例2（2016·江苏无锡）如图2，△AOB中，∠O=90°，AO=8cm，BO=6cm，点C从A点出发，在边AO上以2cm/s的速度向O点运动，与此同时，点D从点B出发，在边BO上以1.5cm/s的速度向O点运动，过OC的中点E作CD的垂线EF，则当点C运动了s时，以C点为圆心，1.5cm为半径的圆与直线EF相切.

【解析】因为EF是△ODB的中位线，EF＝2，

所以DB＝4，又AC∥BD，

图2

【解析】当以点C为圆心，1.5cm为半径的圆与直线EF相切时，CF=1.5，

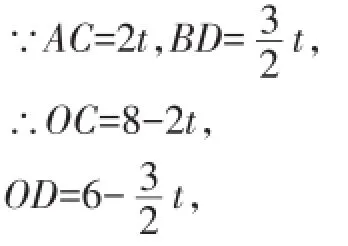
∵点E是OC的中点，

由勾股定理可知CE2=CF2+EF2，

本题综合考查了相似三角形判定、性质和切线的性质，是动态问题，先要通过设未知数t，用t表示线段长度，然后利用勾股定理或相似三角形对应边成比例建立关于t的方程，从而得解.

例3（2016·江苏苏州）如图3，AB是⊙O的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD=BD，连接AC交⊙O于点F，连接AE、DE、DF.

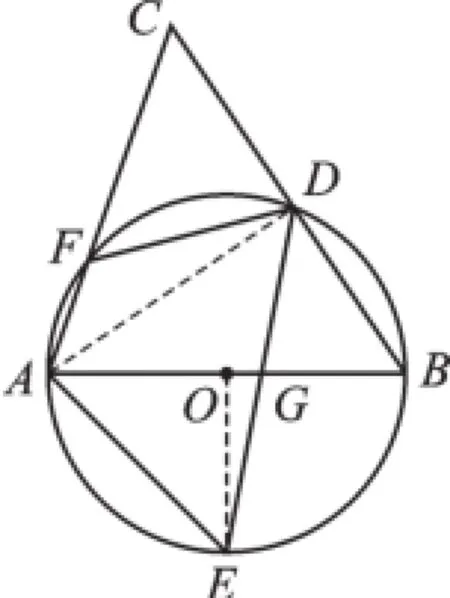
图3

（1）证明：∠E=∠C；

【解析】（1）证明：连接AD，∵AB是⊙O的直径，∴∠ADB=90°，即AD⊥BC，

∵CD=BD，∴AD垂直平分BC.

∴AB=AC，∴∠B=∠C.

又∵∠B=∠E，∴∠E=∠C.

（方法不唯一，也可连接BF进行证明）

（2）连接OE.

∵∠CFD=∠E=∠C，

∴FD=CD=BD=4.

∴AB=6.

∴∠AOE=90°.

即EG·ED=AE2=18.

本题是圆和相似的综合题，关键考查圆中弧、弦、角的转化，由于相似是求乘积比较常用的方法，所以在圆中寻找或构造与EG、ED相关的相似三角形是求解本题的关键.

通过对中考题研究可以发现，相似的主要作用是求比值、求乘积、求线段长以及求与线段长相关的量（比如时间）等.每一道中考题都是学习的宝藏，先探究，再回顾，将解题经验内化为解题技能，相信努力的你会越来越优秀.

（作者单位：江苏省常熟市第一中学）