二次函数典型问题难点突破

张　丽

二次函数典型问题难点突破

张丽

一、二次函数图像问题的处理策略

二次函数作为中学数学学习的核心版块之一，需要同学们熟练地掌握基本性质，能够灵活应用.二次函数的图像，给大家提供了解决问题的工具，熟练应用不仅能掌握本块知识，也能在学习中自然获得逻辑推理、数形结合、函数变化等思想，从而为进一步学习奠定扎实的基础.本文就二次函数图像问题进行分类讨论，以期找到解决这类问题的一般方法.

1.二次函数图像的识图

例1y=ax2+bx+c（a≠0）的图像如图1所示，则点M（a，bc）在（）.称轴在y轴右侧⇒b＜0.由以上条件可知bc＞0.∴点M（a，bc）在第一象限，答案：A.

2.利用已知条件确定函数的图像.

例2已知一次函数y=ax+c，二次函数y= ax2+bx+c（a≠0），它们在同一坐标系中的大致图像是（）.

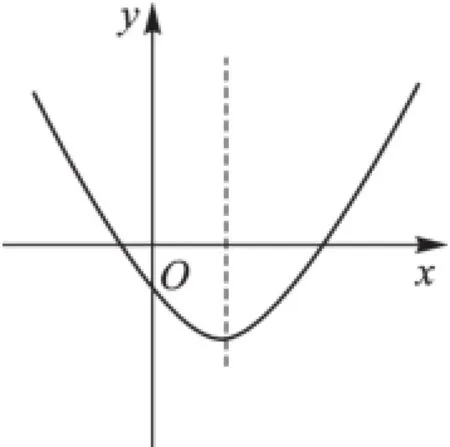
图1

A.第一象限B.第二象限

C.第三象限D.第四象限

【解析】由图可知：抛物线开口向上⇒a＞0；抛物线与y轴的负半轴相交⇒c＜0；对

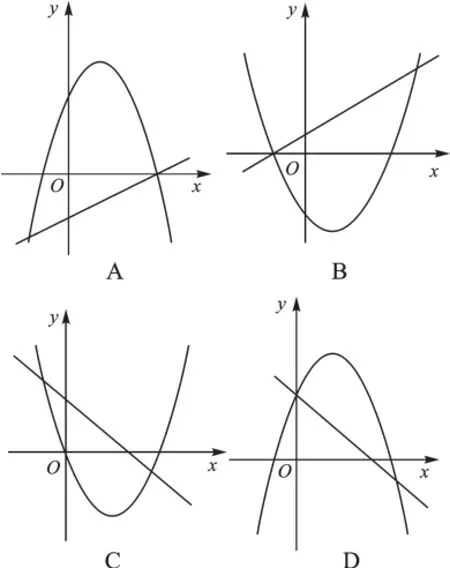
【分析】先讨论a、c的符号情况，判断直线的位置特征；再结合b的符号，考虑抛物线的位置特征.答案：D.

【点拨】一次函数与二次函数的系数用相同字母表示，意味着一次函数的直线图像的倾斜方向与二次函数的开口方向有关联，两个图像的横纵轴的截距有了联系，进而使二次函数对称轴、顶点坐标有了确定的性质，从而能够确定图像.

二、求解二次函数中的面积最值问题的策略

从近几年的各地中考试卷来看，求面积的最值问题在压轴题中比较常见，而且通常与二次函数相结合，使解题具有一定难度.本文以一道中考题为例，介绍几种不同的解题方法，供同学们在解决这类问题时参考.

例3如图2，抛物线y=ax2+bx+c与x轴交于A（1，0），B（-3，0）两点.

（1）求该抛物线的解析式；

（2）设（1）中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；

（3）如图3，在（1）中的抛物线上的第二象限内是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由.

图2

图3

【解析】（1）抛物线解析式为y=-x2-2x+3；（2）Q（-1，2）.

下面着重探讨求第（3）小题中面积最大值的几种方法.

1.补形、割形法.

几何图形中常见的处理方式有分割、补形等，通过对图形的这些直观处理，一般能辅助解题，使解题过程简捷、明快.此类方法的要点在于把所求图形的面积进行适当的补或割，变成有利于表示面积的图形.

方法一：如图4，

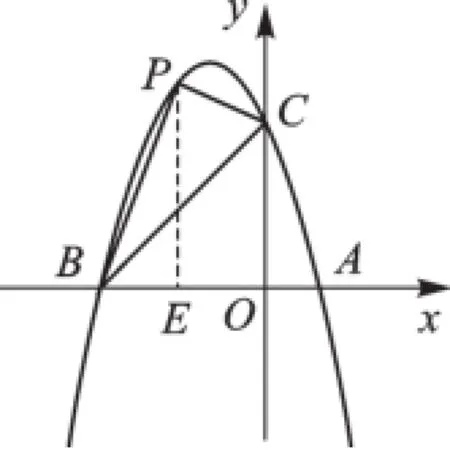
图4

设P点（x，-x2-2x+3）（-3＜x＜0）.

∵S△PBC=S四边形BPCO-S△BOC=S四边形BPCO-

若S四边形BPCO有最大值，则S△PBC就最大.

∴S四边形BPCO=SRt△BPE+S直角梯形PEOC

S四边形BPCO最大值

∴S△BPC最大值

方法二：如图5，

图5

设P点（x，-x2-2x+3）（-3＜x＜0）. S△PBC=S△OBP+S△OCP-S△OBC

2.“铅垂高，水平宽”面积法.

如图6，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”（h），我们可得出计算三角形面积的另一种方法，即三角形面积等于水平宽与铅垂高乘积的一半.

图6

根据上述方法，本题解答如下：

解：如图7，

图7

作PE⊥x轴于点E，交BC于点F.

设P点（x，-x2-2x+3）（-3＜x＜0）.

∵S△PBC=S△FBP+S△FCP

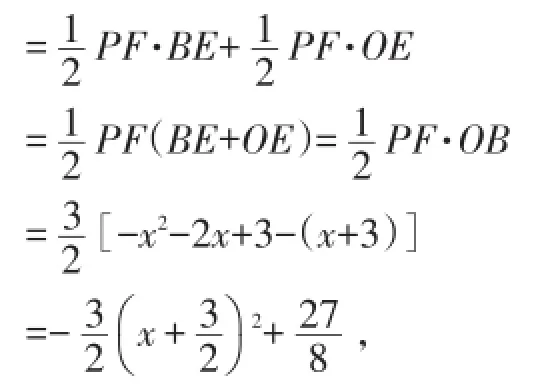
S△PBC最大

三、二次函数与一元二次方程问题的解题策略.

例4已知二次函数：y=（k2-1）x2-（3k-1）x+2.

（1）二次函数的顶点在x轴上，求k的值；

（2）若二次函数与x轴的两个交点A、B均为整数点（坐标为整数的点），当k为整数时，求A、B两点的坐标.

【解析】（1）∵二次函数顶点在x轴上，

∴b2-4ac=0，且a≠0.

即（3k-1）2-4×2（k2-1）=0，且k2-1≠0，

∴k=3.

（2）∵二次函数与x轴有两个交点，

∴b2-4ac＞0，且a≠0.

即（k-3）2＞0，且k≠±1.

当k≠3且k≠±1时，即可.

∵A、B两点均为整数点，且k为整数，

当k=0时，可使x1，x2均为整数，

∴当k=0时，A、B两点坐标为（-1，0）和（2，0）.

【点拨】本题着重考查一元二次方程和二次函数之间的联系，同学们要学会运用函数和方程之间的联系来解决问题.

当然二次函数的典型问题很多，在这里介绍了几种典型问题的解题策略，供同学们参考.如果我们能掌握一定的方法，做到举一反三，那就可以得到事半功倍的效果.

（作者单位：江苏省太仓市第一中学）