分布式电源对配电网的影响及优化配置模型

黄 升



分布式电源对配电网的影响及优化配置模型

黄 升

（湖南电网公司湘潭供电局，湖南湘潭 411100)

随着用电负荷的急剧增长，分布式发电成为了当今电力系统的研究热点。为了更好地发挥分布式电源的经济效应，本文首先对分布式电源接入电网后对传统配电网的影响作了分析研究。在此基础上，建立了电源的优化配置模型，确立了以减少节点电压偏移量、降低系统损耗量和提高并网电压稳定度的多目标函数优化模型，并利用自适应混沌粒子群算法进行函数求解。最后通过算例分析，验证了模型的实际效果和求解算法的准确性。

分布式电源（DG）；多目标优化；自适应混沌粒子群算法

0 前言

随着能源危机的日益严重，分布式电源(DG)以其在经济和生态方面独有的优势，在电能生产中的比重不断增加，成为当今能源领域的重要发展方向之一。DG是为满足某些终端用户的需要，与电网联合运行的，配置在用户侧或负荷集中区域的规模较小的独立电源(一般小于50WM)，主要发电设施包括：光伏发电、风力发电、小水电、内燃机、微型燃气轮机、燃料电池等。DG在给用户带来方便的同时，它的接入也改变了传统配电网络的结构，给电网带来了许多消极影响，包括网损，电能质量，系统保护等方面，因此，研究DG接入配电网的影响和其优化配置问题，对发挥DG的优势和全面推广DG的应用具有重要的研究价值。

文章构建了以节点电压偏移量、系统损耗最少和并网电压稳定度最大的多目标优化模型。为保证算法在多目标函数的准确性和适应性，利用混沌思想，提高粒子种群的多样性和遍历性，择优选择适应度好的粒子，避免陷入局部最优，最后通过案例验证算法的实际效果。

1 DG并网对配电网的影响

DG接入配电网后，首先改变了传统配电系统馈线的潮流大小和方向，对系统网损产生了直接影响。当DG的输出量小于或等于系统中节点的负荷量时，配电网有减少网损的作用。当DG的输出量小于系统中节点的负荷量，同时最少有一个DG的输出量大于该节点负荷量时，配电网可能会使线路损耗增加，当DG的输出量大于系统中节点的负荷量，同时至少有一个DG的输出量大于该节点负荷量时，系统的损耗一定会增加。其次影响了节点电压分布。图1是DG加入前后节点电压的变化。可以看出，DG安装的位置和容量将直接影响节点电压的水平。最后由于传统的配电网是一个单电源系统，一般采用三段式电流保护。DG接入，配电网成为了一个多电源系统，不仅要求设备保护具有方向性而且对线路的保护范围和保护灵敏度都会有影响等。因此建立合适的DG优化模型，对提高系统的稳定性和可靠性，具有重要的意义。

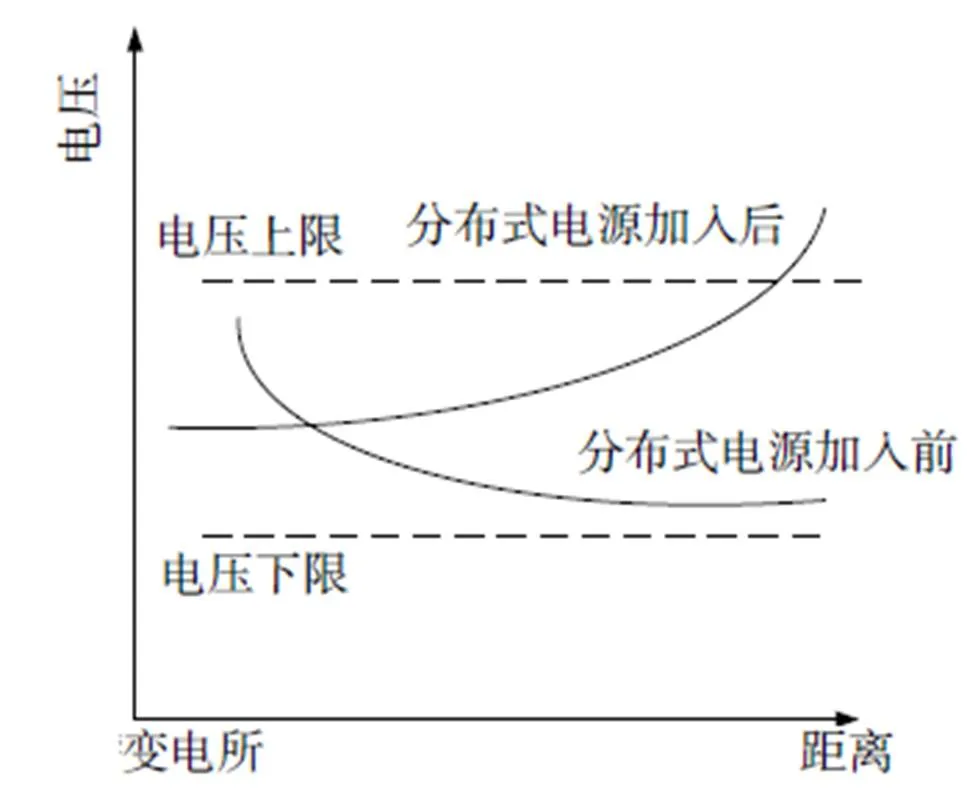
图1 DG加入前后对电压的影响

2 DG优化配置数学模型

2.1 目标函数

目标函数定义为综合节点电压偏移量1、系统网损2和并网电压稳定度3的复合函数，可以写成：

式中，1、2、3是目标函数的权重系数，根据实际情况设定为：1>2>3>0。

以配电网节点电压最小为目标函数1:

以系统网损最小为目标函数2

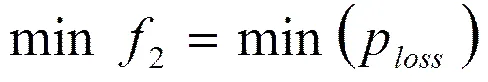
式中，N为支路数总数，G为节点和之间的电导，V、V分别为节点、电压的幅值，为节点之间的电压相角差。

以静态电压稳定裕度最小为目标函数3:

式中，λmin为牛顿潮流方程中雅克比矩阵的最小奇异值。

2.2 约束方程

（1）节点潮流约束方程：

式中：是支路个数；P,i、Q,i分别为节点处电源的有功、无功出力；P,i、Q,i分别为节点处的有功、无功负荷；G、B为系统导纳；δ为节点电压相角差；

（2）节点电压约束方程：

式中：U为节点电压的大小；

（3）支路传输功率约束方程：

（4）分布式电源总容量约束方程：

式中，是节点数；N为DG的个数；P,min和P,max分别表示DG注入有功的上、下限；为DG有功总量占系统负荷总量的比例上限。

3 DG优化配置算法

传统的粒子群算法是基于种群全局搜索的无约束极小优化问题。在寻优过程中，粒子通过跟踪个体最优值best和全局最优值best对自己的位置和速度不断更新，搜索最佳位置。但也会出现陷入局部最优解和后期停滞现象，针对该情况，本文引入了粒子的适应度和混沌算法。算法利用混沌算法特有的遍历性，使粒子跳出局部极值区域，然后自适应的调整惯性系数，使系统时刻保持者较好的全局收索能力。PSO算法为：

利用自适应混沌算法在解多目标函数时的具体流程如下：

（1）初始化多目标函数，设置算法的最大迭代次数和粒子数等参数。

（2）以DG在配电网各节点的注入功率为基本粒子，对个粒子的速度x和位置V进行混沌初始化；

（3）据公式(13)计算种群中个粒子适应值。

min适应度W的最小值，max表示最大值，avg当前目标函数的平均值。

（4）将个粒子适应值的大小，分别与best，和best进行比较，将适应度最小的粒子，赋值给best，best。利用公式（12）（13），更新个粒子速度x和位置V，然后进行潮流计算和对目标函数F求解。

（5）按适应值的大小，择优对前个粒子进行混沌优化，避免陷入局部最优

（6）返回步骤（3）（4），继续进行新的潮流计算和求解。

（7）达到最大迭代次数，结束，返回全局最优解。

4 算例分析

（1）对IEEE33进行实例仿真，验证所提算法的有效性。图2是IEEE33馈线网络模型该配电网电压等级为12.6kV，有功损耗为812.3kW，粒子群算法配置参数：种群规模=50，最大迭代次数100，自适应系数1=0.1345，2=0.7058，3=0.1597，惯性权重上限0.9，下限0.2，学习因子1=3.0，2=2.0，仿真结果如下：

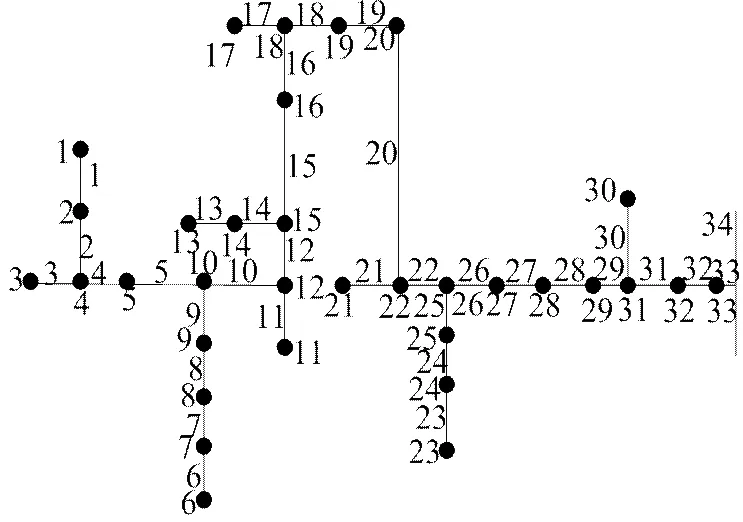
图2 IEEE33馈线网络模型

图3是优化前后节点电压比较图。三角形是优化之前节点电压，五角星曲线为优化之后电压。可以看出优化之后最低电压为0.945p.u.，比优化之前的节点最低电压值得到了有效提高，整体电压水平明显改善。表1是目标量参数，采用该算法后，系统的有功网损由优化前的812.3kW变为498.32kW，降损率约为38.65%，说明该优化配置模型减少了电网网损、降低了发电成本，提高系统灵活性和电压稳定性。

图3 优化前与优化后节点电压比较

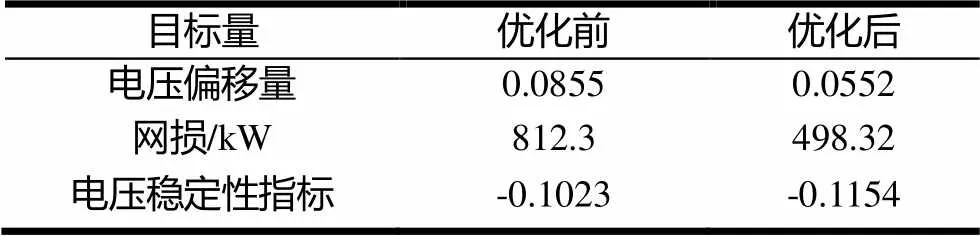
表1 目标量参数

5 结论

本文首先描述了DG对配电网的影响，然后构建了以降低网损，改善电压质量为目标的优化数学模型，并采用自适应混沌粒子群算法进行优化求解。算例表明，进行分布式电源优化配置后，节点电压偏差变小，系统整体性能得到优化。说明该优化配置模型可以达到节省投资、降低损耗、提高电能质量和系统可靠性的目的。

[1] 刘伟, 张海燕, 时婧, 等. 改进PSO与AHP算法优化配置分布式电源网络[J]. 系统仿真学报, 2013, 25(12): 3057-3063.

[2] 贺海, 吕娟, 王磊. 改进粒子群算法在分布式电源优化配置中的应用研究[J]. 2013,29(2):21-25.

[3] 郭伟. 基于ACPSO算法的分布式电源优化配置研究[D]. 长沙理工大学. 2013.

[4] 龚莉莉, 吴红斌. 基于ACPSO算法的含分布式电源配电网无功优化[J]. 合肥工业大学学报, 2014,37(12): 1442-1445.

[5] 陈海东. 基于细菌菌落优化算法分布式电源优化配置[J]. 电力系统保护与控制, 2015, 43(21): 106-111.

[6] 阎鼎. 分布式电源优化配置及其对电能质量的影响[D]. 上海交通大学, 2014.

[7] 陈浩. 分布式电源对配电网网损影响的研究[J]. 电力与能源, 2011(1): 371-372.

[8] 王赛一. 分布式电源及对配电网系统的影响[J]. 上海电力, 2006(5): 515-518.

[9] 张勇, 吴淳. 分布式发电机在配电网中的优化配置[J]. 电力系统保护与控制, 2010,38(11): 33-37.

[10] 叶德意, 何正友, 臧天磊. 基于自适应变异粒子群算法的分布式电源选址与容量确定[J]. 电网技术, 2011,36(6): 155-160.

[11] WANG Caisheng, NEHRIR M H. Analytical approaches for optimal placement of distributed generation sources in power systems[J]. IEEE Trans on Power Systems, 2004, 19(4):2068-2076.

[12] BORGES C L T, FALCAO D M. Optimal distributed generation allocation for reliability, losses, and voltage improvement [J]. Electrical Power and Energy Systems, 2006, 28(6):413-420.

Effect of Distributed Generation on Distribution and Optimal Allocation Model

HUANG Sheng

(Xiangtan Power Supply Bureau of Hunan Power Gird Crop, Xiangtan 411100, China)

With the rapid growth of electricity load, distributed generation has become the hot spot in power systems. In order to better fulfill their economic effects, firstly distributed power grid and then analyzes the impact on traditional distribution network of research . On this basis, and establishes the power of the optimal allocation model establishes the nodal voltage offset, system loss of minimum and max mum grid voltage stability of multi-objective optimization model and adaptive chaotic Particle Swarm Optimization algorithm for solving. Finally, analysis of examples verify the accuracy of the actual effects of the mode land its solution algorithm.

distributed generation(DG); multi-objective optimization; ACPSO

TM722

B

1000-3983(2016)06-0062-03

2015-12-20

黄升（1974-），1995年6月毕业于长沙理工大学电力系电力系统自动化专业，主要从事配电运行维护及配电自动化工作，工程师。

审稿人：宫海龙