一种新型谐波电流双闭环控制策略

张雪珍, 王少杰 王文华

(邵阳学院 机械与能源工程系，湖南 邵阳 422000)



一种新型谐波电流双闭环控制策略

张雪珍, 王少杰 王文华

(邵阳学院 机械与能源工程系，湖南 邵阳 422000)

针对有源电力滤波器负载谐波电流的控制，考虑到逆变器开环运行时动态性能差和电流检测所带来的一些误差，可能导致逆变器的输出电流发生过电流而损坏功率器件。在分析注入式混合有源滤波器的基础上，对传统谐波电流单闭环控制增加一个电流负反馈来控制逆变器的输出电流，实现对谐波电流的双闭环控制。保证了逆变器安全可靠运行，提高了整个系统的抗扰性能以及对给定参考谐波电流的跟随性能，仿真结果验证了谐波电流双闭环控制的可行性与优越性。

谐波电流；逆变器；混合有源滤波器；负反馈；双闭环控制

0 引 言

随着电力电子技术的发展，电力电子设备日益广泛的应用于我国工业和民用领域，使得非线性负荷大量增加，造成电网面临严重的谐波污染[1-2]。电网中存在大量的谐波，一方面会使线路损耗增大，降低电能质量，使功率因素降低，影响系统安全稳定运行；另一方面，电网中的谐波还会对邻近的通信信号产生电磁干扰，影响一定范围的通话质量，甚至在极端情况下，威胁通信设备和人员的安全[3]。

由于电网中谐波的存在给供电部门和用户都造成了极大的危害和损失。因此，国家对谐波的治理制定了相应的控制标准。我国虽然在80年代末才开始研究谐波治理技术，但进展较快，目前在理论、技术与工程应用方面取得了丰富的研究成果与现场应用经验。如西安交通大学、清华大学、湖南大学、西安赛博、上海思源、株洲国变中心、长沙博立电气等大学和企业在有源滤波理论和应用方面做出了杰出的贡献。在学者们的研究基础上，我们总结了许多提高功率因素与谐波治理的方法[4-5]，如：通过无功补偿屏提高功率因素、采用消谐滤波补偿装置、无源滤波器、有源滤波器等等。目前，如何对电网中的谐波进行优化治理仍是学者们竞相研究的热门课题。

本文针对注入式混合有源滤波器(Injection Hybrid Active Power Filter, 简称IHAPF)提出了一种新型谐波电流双闭环控制策略。利用广义积分控制器[6]137-146对注入支路输出电流实现零稳态误差控制，但是由于广义积分器常用于只考虑有限的几次谐波的情况，而对于谐波频率过多的情况实现起来比较繁琐，进行仿真的系统结构框图也比较复杂。因此，本论文采用递推积分PI控制器，同样能实现对系统的无差控制，且其传递函数形式相对简单，仿真易于实现。该控制策略大大减小了基波电流流入逆变器时输出电流的增益并且能够获得较好的动态跟随性能。

1 注入式混合有源滤波器拓扑结构

图1 IHAPF系统结构示意图

图2 低压侧折算至高压侧的单相等效电路图

图3 简化后的等效电路图

注入式混合有源滤波器拓扑结构如图1所示，整个有源滤波器系统由供电和传输线路、非线性负载、注入支路、耦合变压器、输出滤波器及电压型逆变器组成[6]80-115。从图1可以看出，注入支路的电容C1和电感L1构成基波串联谐振电路，目的是使得很少的基波电流流入耦合变压器和逆变器，大大减小逆变器的容量。基波串联谐振电路电容CS(即注入电容)一方面补偿电网基波无功，另一方面尽量使有源滤波器的输出电流注入到电网以治理电网谐波。为便于下文的分析，输出滤波器(Output Filter, 简称OF)采用简单的L型，用于滤除逆变器功率器件的开断所带来的高频毛刺。直流侧电容和电压型逆变器构成有源部分，用于改善整个滤波系统的滤波性能和滤波效果，抑制无源滤波器和电网电感形成的串并联谐振，弥补无源电力滤波器存在的缺陷和不足[7-8]。

在对注入式混合有源电力滤波器进行建模时，将有源滤波器输出看成谐波电压源，将非线性负载看成谐波电流源，将逆变器看成受控电压源，从而可以得到系统从低压侧折算至高压侧的单相等效电路图(如图2所示)。

由于本论文所讨论的谐波电流主要为负载电流，因此可将图2进行简化，在这里假设电网电压输入为正弦波，其谐波忽略不计。这样由逆变器输出的谐波电流经注入支路与非线性负载产生的谐波电流相互抵消。可得简化后的等效电路图如图3所示。

根据基尔霍夫电压定律与基尔霍夫电流定律能得到如下方程：

(1)

(2)

I0(S)=I1(S)+IFh(S)

(3)

UF(S)=I0(s)L0+U1(S)

(4)

IFh(S)=-ILh(S)

(5)

2 注入式混合有源滤波器控制方法

有源滤波器相对于无源滤波器而言是一种动态的、灵活的谐波治理手段[9-10]。而有源滤波器的这些优良性能的实现在很大程度上依赖于对PWM逆变器的控制上。因此，采取一定的控制策略对逆变器开关模式进行控制，使逆变器输出的谐波电流能较好的跟踪给定的参考谐波电流以消除谐波，达到谐波治理的目的，是有源滤波器研究的关键[11-12]。

根据图1，可画出传统的IHAPF单闭环控制系统结构如图4所示。

图4 单闭环控制系统结构图

由公式(1)至(5)，可以画出IHAPF单闭环控制系统结构框图(如图5所示)。

图5 IHAPF单闭环控制系统结构框图

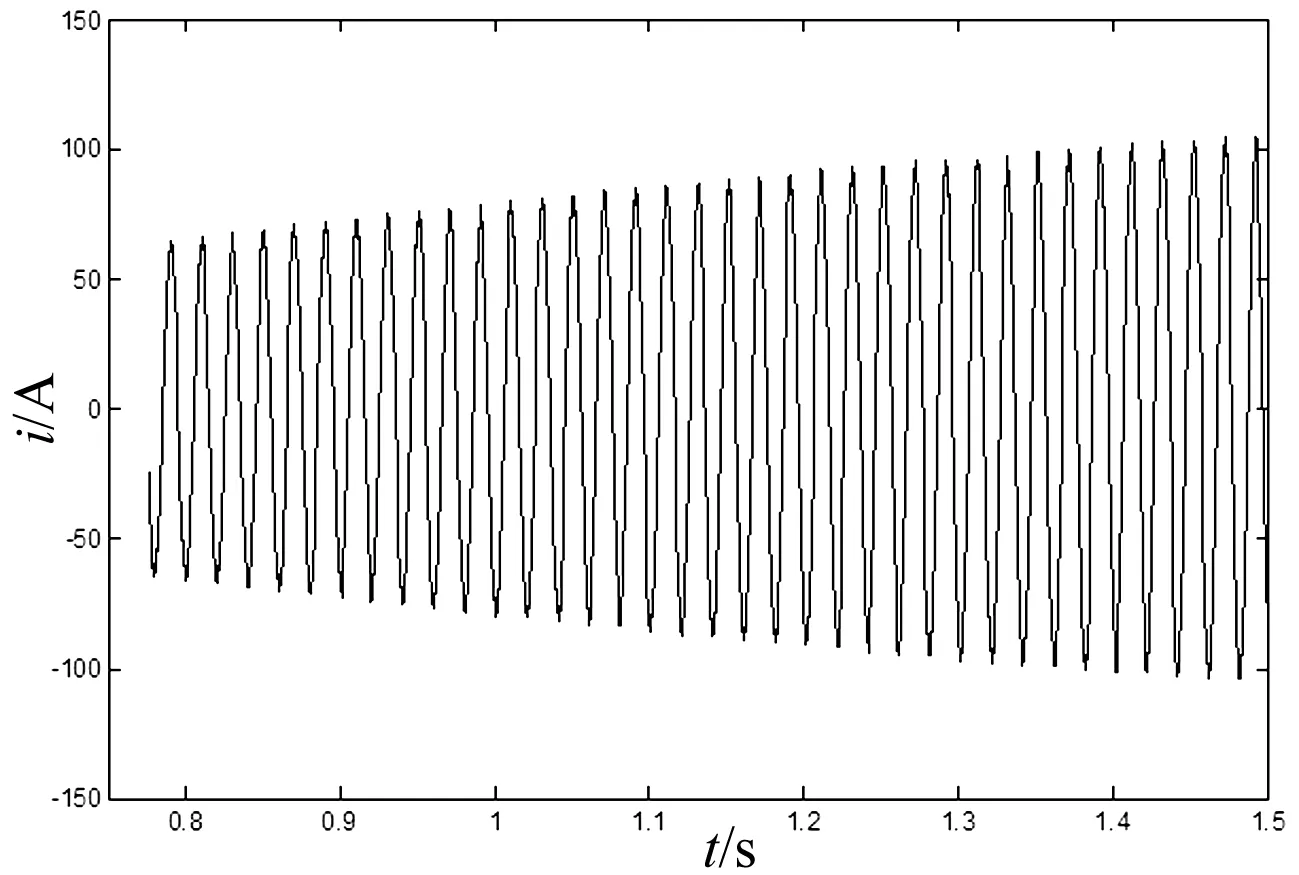
图6 逆变器输出电流I0波形

图7 注入支路电流IF波形

对传统的IHAPF单闭环控制系统进行MATLAB/Simulink[13-15]仿真，仿真所取参数为：CS=100 μF,C1=400 μF,L1=25.33 mH,L0=0.25 mH。由于在进行谐波电流检测时存在的一些检测误差，因此，谐波检测装置不可能完全滤除基波电流，这样便使得作为参考的谐波电流中带有很小一部分的基波电流[11]。这个很小的基波电流经逆变器可能产生很大的输出电流I0，而这个输出电流I0绝大部分流入基波串联谐振电路，因此在注入电流IF中几乎检测不到这个很大的逆变器输出电流，也不可能经反馈环节加以抑制。例如：当有幅值为0.1 A，相位为零的基波电流流入逆变器时，仿真结果如图6、图7所示。从仿真图可以看出逆变器的输出电流I0会有很大的增益，其增益约为1 000倍，而注入支路电流IF增益不大，约为25倍远远小于1 000。逆变器输出电流过大会烧毁功率器件，因此，需对逆变器的输出电流加以限制。根据自动控制原理，要维持被调量很少变化或基本不变，通常的思路是将被调量作为反馈量引入系统。而本文将逆变器的输出电流作为反馈量引入系统，与之前的单闭环控制系统构成双闭环控制系统。

3 新型双闭环控制策略及仿真

双闭环控制系统结构框图如图8所示。其中内环采用PI调节器，而对于外环，由于被控制量为正弦量，用传统的PI调节器进行控制会产生稳态误差。本文采用一种基于递推积分的PI调节器，实现对系统的误差控制，从而达到良好的动态跟随性能与鲁棒控制性能。

图8 双闭环控制系统结构框图

图9 逆变器输出电流I0波形

假设流入逆变器的基波电流幅值仍为0.1 A，相位为零，通过仿真发现其增益为6远远小于采用单闭环控制的输出电流1 000。仿真结果如图9所示。

对于采用递推积分PI调节器[8]控制的外环，研究其对于给定参考谐波电流信号的跟随作用。传统PI算法的离散形式如式(6)所示，式中u(K)为K时刻的控制器的输出，e(K)为K时刻的误差采样值，KP、KI分别为比例系数和积分系数。这种离散形式PI算法是对误差进行逐点积分[6]137-146。

(6)

递推积分PI算法如式(7)所示，式中u(K)为K时刻的控制器的输出，e(K)为K时刻的误差采样值，N为一个周期内的采样数，KP、KI分别为比例系数和积分系数，C为K/N取整。这种算法相当于对误差逐周期积分。

(7)

为简化计算，可利用u(K)的增量形式进行计算。在K-N时刻，式(7)可改写为：

(8)

将式(7)减去式(8)得：

△u(K)=KP·e(K)-KP·e(K-N)+KI·e(K)

(9)

也可表示成:

u(K)=u(K-N)+KP·e(K)-KP·e(K-N)+KI·e(K)

(10)

将上式写成s域的传递函数为，

(11)

式中T为采样时间间隔，NT=20 ms。从上式可以看出，递推积分PI调节器的传递函数包含了参考信号的周期信息，但是传统的PI 调节器不包含这些信息。

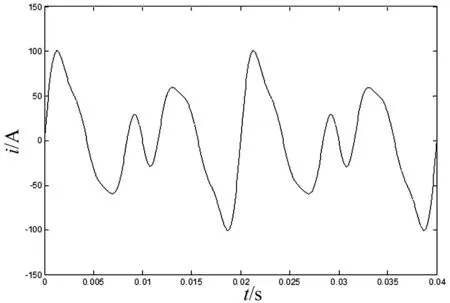
图10 参考谐波电流波形

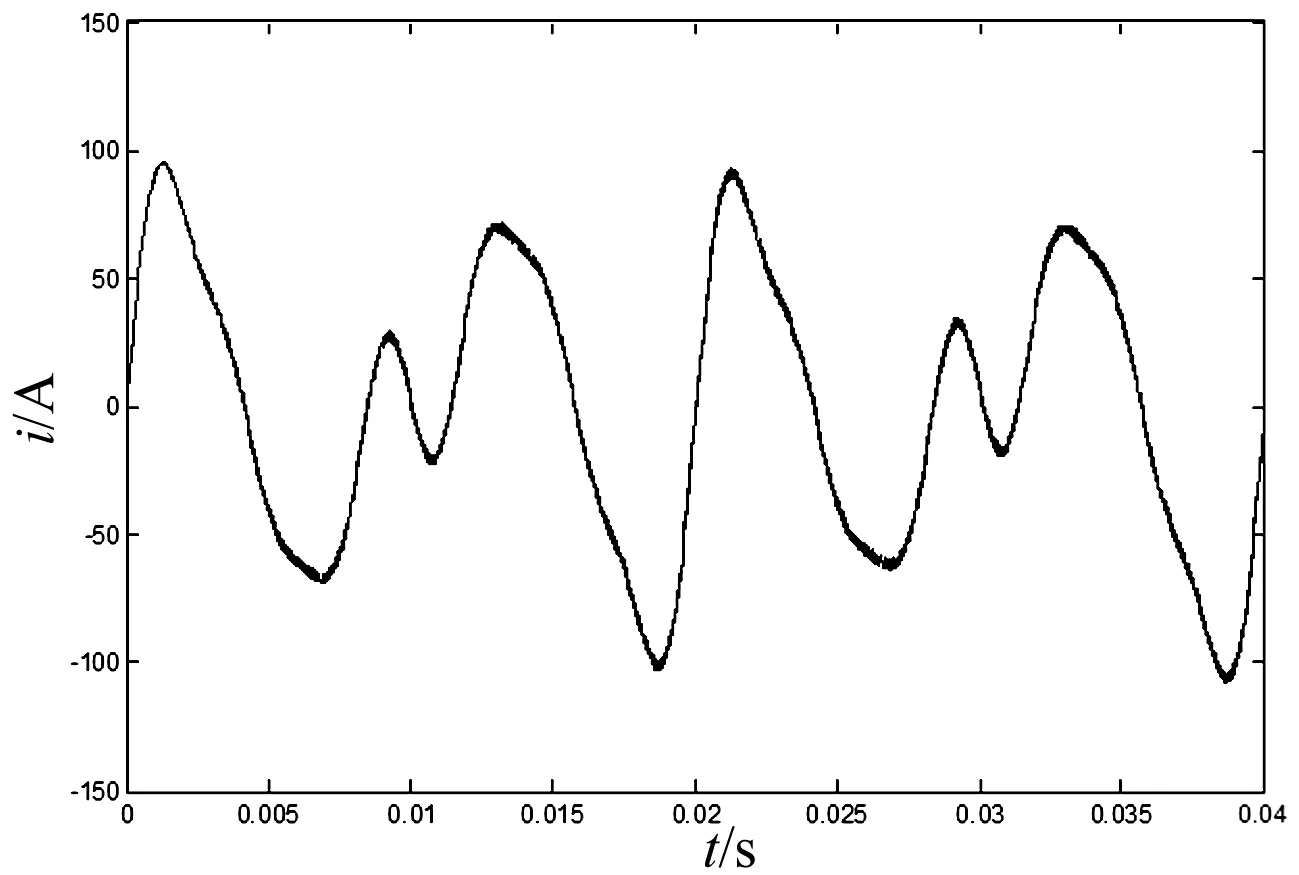
图11 注入支路输出电流波形

为了验证递推积分PI调节器具有较好的动态跟随性能和控制精度，当给定的参考谐波信号分别为：2次谐波幅值58 A，3次谐波幅值为40 A，5次谐波幅值20 A,7次谐波幅值11 A，相位均为零时。取递推积分PI调节器的参数为：KP=20,KI=200，观察给定参考谐波电流与注入支路输出电流波形，如图10，图11所示。

4 结束语

从逆变器输出电流对于基波增益过大和采用单闭环控制时谐波注入电流对检测电路中给定的参考电流动态跟随性能不理想这两个问题对注入式混合有源电力滤波器进行分析。以逆变器的输出电流作为反馈量引入系统，大大减小了基波电流的增益；用递推积分PI调节器取代传统的PI调节器，获得了较好的动态跟随性能。通过对仿真结果的分析，表明基于递推积分PI控制算法的谐波电流双闭环控制策略具有一定的优越性与可行性。

[1] 吴竟昌.供电系统谐波[M].北京:中国电力出版社,1998.

[2] 林海雪,孙树勤.电力网中的谐波[M].北京:中国电力出版社,1998.

[3] 李剑,康勇,陈坚. 单相SPWM逆变器的死区效应分析和补偿策略[J]. 电气传动，2009,51(1)：12-17.

[4] 王少杰,罗安.混合有源电力滤波器新型控制策略及稳定性分析[J].电工技术学报,2011,26(6):144-152.

[5] 王兆安,杨军,刘进军.谐波抑制和无功补偿[M].北京:机械工业出版社,1998.

[6] 罗安.电网谐波治理与无功补偿技术及装备[M].北京:中国电力出版社,2006.

[7] 阮毅，陈伯时.电力拖动自动控制系统——运动控制系统[M].北京:机械工业出版社，2009.

[8] 孙贤大,罗安,帅智康,等.注入式混合型有源电力滤波器双闭环控制[J].电工技术学报,2009,24(9):127-133.

[9] 徐永海,肖湘宁,刘昊,等.混合型有源电力滤波器与并联电容器组联合补偿技术研究[J].电工技术学报,2009,24(1):112-117.

[10] 颜晓庆,王兆安.并联型电力有源滤波器控制方式对动态特性影响的研究[J].西安交通大学学报,1998,32(6):26-30.

[11] 黎燕,罗安.双谐振混合型有源电力滤波器特性研究[J].电工技术学报,2012,32(9):258-260.

[12] 王群,姚为正,刘进军,等.谐波源与有源滤波器的补偿特性[J].中国电机工程学报，2001,21(2):16-20.

[13] 赵广元.MATLAB与控制系统仿真实践[M].北京:北京航空航天大学出版社,2012.

[14] 卓金武.MATLAB在数学建模中的应用[M].2版.北京:北京航空航天大学,2014.

[15] 周品.MATLAB图像处理与图形用户界面设计[M].北京:清华大学出版社,2013.

A Novel Control Strategy of Double Closed Loop for Harmonic Current

Zhang Xuezhen, Wang Shaojie, Wang Wenhua

(Shaoyang University Department of mechanical and energy engineering, Shaoyang Hunan 422000, China)

Aiming at the control of harmonic current of the load, in consideration of the bad dynamic performance of inverter with open-loop operation and some error caused by current detection, may cause the output current of the inverter accessed and then damage power devices. This paper based on the foundation of traditional single closed-loop control increase a current negative feedback to control output current of the inverter, in order to achieve the double-closed loop control of harmonic current. The method ensures the safe and reliable operation of the inverter, improving immunity performance of the entire system as well as the follow performance of a given reference harmonic current. Simulation results show the feasibility and superiority of harmonic current double closed-loop control.

harmonic current; inverter; hybrid active power filter; negative feedback; double closed-loop control

湖南省教育厅重点科研项目(13A089)；湖南省教育厅优秀青年科研项目(12B116)

10.3969/j.issn.1000-3886.2016.04.008

TM712

A

1000-3886(2016)04-0024-03

张雪珍(1990-)，女，湖南邵阳人，研究生，从事高电能质量输配电技术研究。 王少杰 (1974-)，男，博士，副教授，研究生导师，从事高电能质量输配电技术研究。

定稿日期: 2016-01-18