九位不同数字乘法等式的优化算法
2016-12-07陈勇
陈勇
(遵义职业技术学院,贵州 遵义 563000)
九位不同数字乘法等式的优化算法
陈勇
(遵义职业技术学院,贵州 遵义 563000)
对“九位不同数字构成乘法等式”的问题进行研究分析,深入探讨其解决方案,根据NP问题穷举算法设计的常规思路,设计了一种更加优化的穷举算法,实验证明该算法是正确高效的。
NP问题;穷举算法;优化算法;高效
1 引言
文献[1]使用数字{1,2,3,4,5,6,7,8,9}组成形如X×Y=Z的乘法等式,在该等式中使用且仅使用九个数字中的每个数字一次,列举出了所有符合条件的等式。“九位不同数字构成乘法等式”的问题显然是NP[2]问题,采取常用数学分析算法求解非常困难,此类问题常采用穷举算法求解[3]。实现的具体方法很多,用递归与非递归回溯算法实现比较耗时,本文提出了一种基于预处理[4]的更加优化的穷举算法,其算法大大减少了程序运行的时间。
2 问题分析
根据文献[1]可知,9个数字分别为任意的且互不相同的a1,a2,a3,…,a9,所谓符合条件的等式其实是在排列a1a2a3a4a5a6a7a8a9中找到可使等式成立的乘号、等号的位置,即确定两个因子的数字位数。满足等式有两种情形(排除乘法交换律的等价等式):
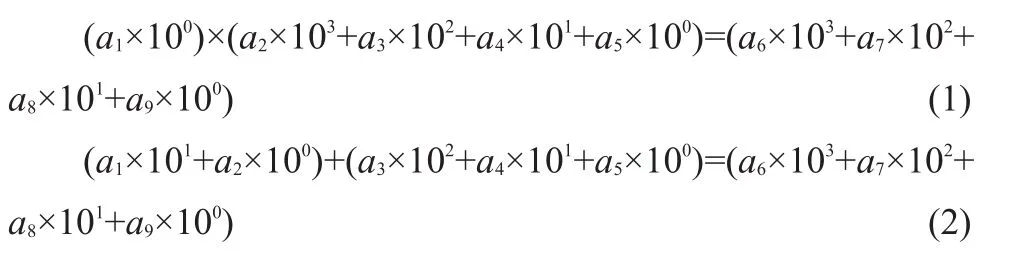
穷举数字{1,2,3,…,9}的所有排列非常耗时,通过分析发现只要穷举乘积的排列就可大大减少计算时间,即乘积范围为1234~9876。进一步研究缩小乘积范围,在(1)式中最小的乘积是1×2345=2345,但1位数字因子不可能是1,那么最小的1位因子只可能大于等于2,因此构造另一个最小的乘积是2×1345=2690,根据数字互不相同的规则容易得出,满足等式的最小乘积至少大于3000;同理可知,23×145是(2)式中最小的因子组合,而其积3335也不满足数字互不相同的规则,这也说明最小乘积至少大于3000,由于1或者2用于因子,那么最小乘积至少为3456。因此,进一步缩小乘积的范围是3456~9876。
3 算法设计
(1)在3456至9876中按序取1数,如果已取完则执行(9);
(2)所取数的4位数字用预处理判断是否相异,否则执行(1);
(3)所取数是否被2~9中某一数整除,否则执行(6);
(4)商为4位数且9个数字相异,否则执行(6);
(5)输出一个解;
(6)所取数是否被12~98中某一数整除,否则执行(1);
(7)商为3位数且9个数字相异,否则执行(1);
(8)输出一个解,执行(1);
(9)结束。
4 算法实现
4.1 算法预处理
用预处理判断乘积中4个数字是否重复,即在穷举乘积的排列时,用预处理过滤掉乘积中有相同数字的乘积,减少搜索空间。
int judge1(int x)
{
int a,b,c,d;
a=x/1000;
b=x%1000/100;
c=x%100/10;
d=x%10;
if(d==0||b==0||c==0) return 0;
if(a==b||a==c||a==d) return 0;
else if(b==c||b==d||c==d) return 0;
else return 1;
}
4.2 判断乘积等式是否符合条件
int judge2(int x,int y,int z)
{
int a,b,c,d; int a2,b2;
int a3,b3,c3,d3; a=x/1000;
b=x%1000/100; c=x%100/10; d=x%10; if(y<10) {
a2=y;
a3=z/1000;
b3=z%1000/100; c3=z%100/10;
d3=z%10;
b2=0;
if(b3==0||c3==0||d3==0)
return 0;
}
else
{
a2=y/10; b2=y%10; a3=z/100;
b3=z%100/10;
c3=z%10;
d3=0;
if(b3==0||c3==0||b2==0) return 0;
}
if(a==a3||a==b3||a==c3||a==d3||a==a2||a==b2) return 0;
else if(b==a3||b==b3||b==c3||b==d3||b==a2||b==b2) return 0;
else if(c==a3||c==b3||c==c3||c==d3||c==a2||c==b2) return 0;
else if(d==a3||d==b3||d==c3||d==d3||d==a2||d==b2) return 0;
else if(a2==a3||a2==b3||a2==c3||a2==d3) return 0;
else if(b2==a3||b2==b3||b2==c3||b2==d3) return 0;
else if(a3==b3||a3==c3||a3==d3) return 0;
else if(b3==c3||b3==d3||c3==d3) return 0;
else return 1;
}
4.3 乘积等式搜索for(i=3456;i<9877;i++)
{
if(judge1(i)==0)
continue;
for(j=2;j<10;j++)
{ if(i%j==0)
{
k=i/j;
if(k/1000==0)
continue; if(judge2(i,j,k)==0)
continue; tnum++;
printf("%d*%d=%d ",j,i/j,i);
}
}
for(j=12;j<99;j++)
{
if(j/10==j%10) continue; if(i%j==0)
{
k=i/j;
if(k/100==0)
continue; if(judge2(i,j,k)==0)
continue; tnum++;
printf("%d*%d=%d ",j,i/j,i);
}
}
}
printf("共有%d种 ",tnum);
5 实验测试及结论
经过计算共得到如下9组解(与文献[1]的解相同):
28*157=4396;18*297=5346;27*198=5346;
12*483=5796;42*138=5796;4*1738=6952;
39*186=7254;48*159=7632;4*1963=7852;
由文献[3]可知该算法的时间复杂度为O(n)。在操作系统xp和CPU为AMD 4600+(2.4G)的环境下用C语言实现,五次测试其平均值为8ms,由此可见本算法是高效的;通过检验本算法所得答案也是正确的。
[1]白宇.九位不同数字乘法等式的递归与非递归回溯算法[J].山西大同大学学报(自然科学版),2009,25(4):12-14.
[2]Aho Alfred,Ullman Jeffrey,Hopcroft et al.The design and analysis of computer algorithms[M].北京:机械工业出版社,2007.
[3]Levitin Anany,潘彦[译].算法设计与分析基础[M].北京:清华大学出版社,2004.
[4]姜华林.数独问题高效算法的研究与实现[J].计算机光盘软件与应用,2013(12):82-83.
An Efficient Algorithm for the Equation of Multiplication of Nine Different Single Numbers
Chen Yong
(Zunyi Vocational and Technical College,Zunyi 563000,Guizhou)
Based on the study of the equation of multiplication of nine different single numbers and according to conventional design for NP problem by exhaustive algorithm,the author introduces an optimized algorithm to solve the famous puzzle.It is improved that the algorithm is correct and efficient.
NP problem;exhaustive algorithm;optimized algorithm;efficient
TP302
A
1008-6609(2016)07-0046-03
陈勇,男,贵州遵义人,讲师,研究方向:媒体制作与网站建设。
