基于NP证据加密的可撤销广播加密方案构建

郭　韧，陈福集，程小刚

(1. 福州大学经济与管理学院　福州　350116；2. 华侨大学工商管理学院　福建 泉州　362021；3. 华侨大学计算机学院　福建 厦门　361021)

基于NP证据加密的可撤销广播加密方案构建

郭韧1,2，陈福集1，程小刚3

(1. 福州大学经济与管理学院福州350116；2. 华侨大学工商管理学院福建 泉州362021；3. 华侨大学计算机学院福建 厦门361021)

NP(non-deterministic polynomial)证据加密(witness encryption,WE)是近来提出的一种新型的没有密钥生成过程的加密方案，可以用来构建许多其他的密码系统如公开密钥加密、IBE(identity based encryption)、ABE(attribute based encryption)等。该文提出WE的一种新应用：用WE构建可撤销广播加密系统，并且所构建的广播加密方案能支持简单的成员重加入功能(如付费电视)；在构建的过程中指出以前的WE安全性定义不够严格，对原WE安全性定义进行了增强，并基于原WE方案和子集成员分辨难题、ROM(random oracle model)模型提出了一个新方案。

广播加密;子集成员分辨难题;成员撤销;NP证据加密

WE是文献[1]提出的一种新的没有密钥生成过程的加密系统，它以一个NP语言(NP语言是一个能在多项式时间内被一台非确定图灵机所接受的语言)L的实例x作为公钥对消息m进行加密。如果x∈L且解密者有相关的NP证据w，则可以对密文解密得到消息m；若x∉L，则加密是语义安全的(semantic secure)。文献[1]给出了WE的多种应用，如公钥加密方案、IBE和ABE等。

广播加密(broadcast encryption,BE)[2]典型的应用是付费电视，电视台对视频节目进行加密后广播出去，任何人都可以收到加密后的视频，但只有付过费的合法用户(拥有相关密钥)才能解密正常收看电视节目。

本文提出WE的另一个应用，即用于构建可撤销的BE方案[3-4]，所构建的可撤销BE方案具有简单的成员重新加入功能，此功能适合类似付费电视等相关的应用：欠费的用户被停机，而当用户缴清欠费后又要恢复其成员资格。在构建的过程中，指出了原来的WE安全性定义对本文的应用来说不够严格，为此对WE的安全性定义进行了加强。

基于WE来构建BE方案的思想如下：BE系统中用户的解密私钥是电视台颁发的一个签名(如对其用户名的签名)，加密时使用WE方案进行视频加密。在加密方案构建中所基于的NP语言L是，其实例x是一个签名方案的验证公钥PKSign，NP证据就是一合法的消息/签名对(ID,δ)；对于合法的BE系统用户，其拥有合法的消息/签名对(即合法的NP证据)能解密密文；对于非法用户，由于其没有相关NP证据就不能解密密文(要对原WE安全性进行加强，因原定义只对x∉L的情况进行了规定，没考虑到x∈L但解密者没有相关NP证据w的情况)；这只是实现了BE的基本功能，为了撤销某个用户，系统还要维护一个撤销列表(revocation list,RL)，保存所有被撤销用户的名单，并在每次有用户被撤销时，将原NP语言进行更新，即：

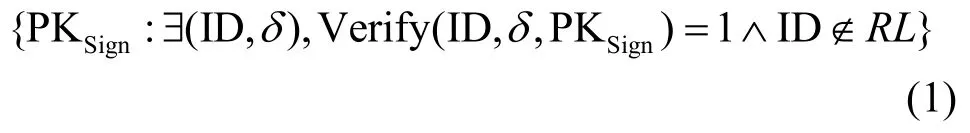
这样被撤销的用户就不再拥有对此NP语言的合法证据(因其ID在撤销列表RL中)，也就不能再对广播密文进行解密；而假如某撤销用户要重新加入时(如其缴清欠费)，系统只要从RL中把该用户的ID删除即可。

1　理论知识

本节给出NP证据加密WE及其安全性的定义、广播加密BE的定义及其安全模型。

定义1WE方案：针对NP语言L的WE方案有如下的多项式时间算法。

ENC(1λ,x,M)：输入安全参数λ、字符串x和待加密的消息M，输出密文CT；

DEC(CT,w)：输入密文CT、字符串w，输出消息M或特殊字符⊥。

并且这些算法满足下面的性质：

正确性：如果x∈L且w是相应的NP证据，那么解密算法总能正确解密得到消息M，即：

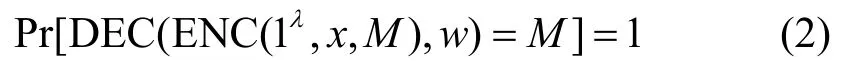
公正性：如果x∉L，那么对于任何的多项式时间敌手A来说，除了可忽略概率之外，对两个不同消息m0和m1加密的密文分布是相同的，即：

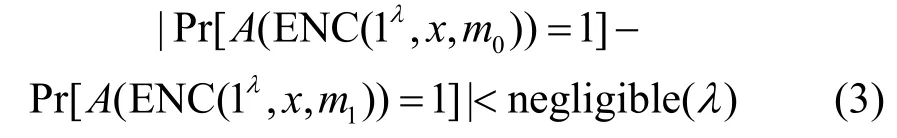
文献[1]基于多线性映射[5]构建了一个具体的WE方案，所基于的NP语言L为NP完全问题——子集覆盖问题[6]，但其缺陷在于所基于的数学假设同此NP问题是紧密相关的；为此文献[7]中提出了基于独立于所用NP语言假设的WE构建[7]，所用的技术是另一种基于整数的多线性映射方案[8]，但文献[8]中的方案最近被完全攻破[9]，因此文献[7]的构建也是不安全的，构建基于独立于所用NP语言假设的WE方案仍是重要的公开问题。

另外在此定义中存在一种重要的情况没有被安全定义，即敌手A知道x∈L，但A不知道相关的NP证据的情况。

下面给出可撤销广播加密方案的定义和安全模型定义。

定义2构成BE的多项式算法如下：

1)setup: 生成系统的主公/私钥对MPK/MSK，并初始将RL设置为空；

2)join: 标识为ID的用户向系统申请加入，系统管理员审核后由(MSK,ID)生成用户私钥SKID并颁发给用户；

3)ENC(MPK,m,RL)：用系统公钥MPK及RL对消息m进行加密，得到密文CT；

4)DEC(CT,SKID)：任何合法的用户(具有合法的私钥SKID，且其ID∉RL)，可对密文CT进行解密得到消息m；

5)revo：系统管理员将欲撤销的用户的标识ID放入RL中去，标识其以后不再能收到消息；

6)re-join：系统管理员将用户ID从RL中删除，此后该用户就能正常接收广播消息。

定义3BE的抗明文攻击安全性(indistinguishable against chosen plaintext attack,IND_CPA)：

1)challenger生成BE方案的MPK/MSK，并把MPK发送给敌手ADV；

2)ADV能自适应地向challenger查询任一个标识为ID的用户的私钥，challenger利用其掌握的MSK生成私钥，并发送给ADV，并将所有ADV查询过的ID加入到集合Q中；

3)ADV生成任意两个长度相同但内容不同的消息m0、m1，并发送给challenger；

4)challenger首先将集合Q中的所有用户放入RL中去，再随机选择b=0或1，用MPK和RL对mb进行加密得到密文CT，将密文发送给ADV；

5)ADV收到CT后，要猜测b=0还是1，称BE是IND_CPA安全的，如果ADV的成功概率同1/2的差是可忽略的，即：

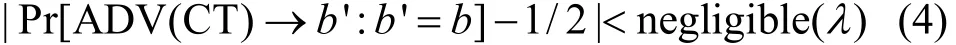
2　构建

2.1WE安全性增强与扩展

定义4增强的WE除了要满足原来的正确性、公正性之外，还要满足第三个安全性质——特别公正性(special soundness)：即使敌手A知道x∈L，但他没有相关的NP证据w，那么加密对他来说仍然是语义安全的，即：

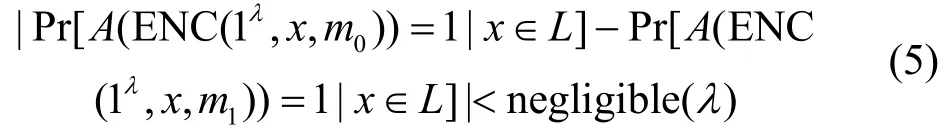
下面基于原来的WE方案和子集成员分辨难题(hard subset membership problem,HSMP)来构建一个满足特别公正性的方案。

所用的NP语言L为一个HSMP问题，如DDH[10]、DLIN[11]或任一个矩阵DH[12]等，为简单起见，下面的叙述以DDH为例，其他的HSMP问题也一样可以。

著名的DDH问题就是要把元组(gr,hr)和分辨开来，NP语言是，NP证据是r；此语言的一个实例是两个群元素，增强的WE构建是利用原来的WE方案，并用此DDH语言作为所用的NP语言来加密消息。

WE. setup：把上述的DDH问题规约到一个子集精确覆盖(exact cover)问题，因为精确覆盖问题是一NP完全问题，此种规约一定存在，然后用原WE方案进行加解密操作；

WE.ENC：前面所得的精确覆盖问题x，即若干子集Ti和全集[n]，对于给定的消息M，随机选择n个数，计算，此外对每个子集Ti生成，最后输出密文

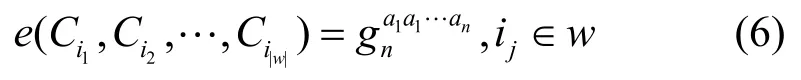
定理1 上述的基于DDH语言的WE方案除了满足原来的WE安全性之外，如果DDH假设成立，那么还满足增强的特别公正性。

2)公正性

3)特别公正性

假设存在敌手A此时能打破密文的语义安全性，证明利用此敌手A就能攻破DDH假设，归约方法如下：

给定两个群元素(G,H)，要判定其是否为DDH元组，只要利用此元组作为一个NP语言实例x来加密从m0、m1中随机选择的消息mb，然后将密文发给敌手A，那么基于A猜测的正确性，就能知道(G,H)是否为DDH元组。如果A的猜测是正确的，那么(G,H)是DDH元组，因为此时恰为而A没有相应NP证据的情况，根据A的定义他猜测正确的概率较大；如果A的猜测是错误的，那么显然，因为此时根据原来的WE方案的安全性(即x∉L的情况)，任何人都不能打破密文的语义安全性。

上述构建的一个缺陷是通常HSMP问题都不是NP完全问题(如DDH、DLIN等)，而理论上不能把任一NP问题都归结为HSMP问题，这就制约了WE的许多应用。实现针对一个NP完全问题的具有特殊公正性的WE方案是一个有趣的公开问题。

对上述构建进行扩展，使其能直接用于构建BE方案。所用的NP语言是基于ROM模型[13]的一个签名方案(或称为Fiat-Shamir转换[14]，把交互式零知识证明系统转换为非交互式知识签名(signature of proof of knowledge,SPK)[15])。该签名方案的公钥(G,H)=(gr,hr)，签名，实现方法如下：

此扩展的WE方案满足特别公正性的证明基本上同定理1的证明是相同的，即如果存在打破特别公正性的敌手，那么能利用敌手来攻破DDH假设。

2.2基于增强WE的BE方案构建

下面基于增强的WE方案来构建可撤销的BE方案：

1)KeyGen：生成上述基于SPK签名方案的PK/SK作为MPK/MSK，即公钥(,)(r,r)G H=g h ，私钥为r，初始时将撤销列表RL设置为空，即没有用户被撤销。

2)UserKeyGen(ID)：对名为ID的用户颁发证书为ID的签名，即，用户可以检查其证书是否合法，即Verify(ID,δ)=1是否成立。

3)ENC(m)：对消息m进行加密是用前述的WE方案加密得到的密文CT，所用的NP语言L为：

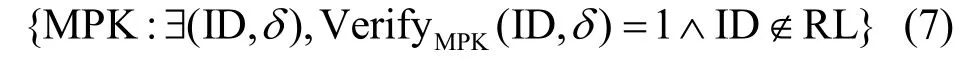
针对验证公钥MPK存在一合法的消息/签名对(ID,)δ，其中消息ID不在撤销列表RL中(RL开始为空，每撤销一个用户就把其ID加入RL中去)。

4)DEC(CT)：对于合法的用户其拥有合法的消息/签名对(ID,)δ，且其ID不在RL中，也即其拥有针对上述NP语言合法的NP证据，则显然可以利用WE方案的解密算法对密文CT进行解密得到消息m；对于非法的用户，其没有消息/签名对，或者其ID已在RL中，都没有合法的NP证据，也就不能对用WE方案加密的密文进行解密。

5)Revo：撤销某用户时，只要将其ID加入到RL中，同时也要更新此后要发广播消息时用的NP语言L，在L中要使用最新的撤销列表，来排除刚撤销的用户。

6)Re-join：假如RL中某被撤销用户要重新加入(如用户缴清欠费等)，系统管理员只要从RL中将其ID删除即可。

2.3性能与比较

上述BE和WE方案构建中，由于要把DDH语言的实例规约为NP完全问题——精确覆盖问题，这种规约通常效率较低，所以本文提出的基于WE的BE方案是理论上的方案构建，还不能够应用于实际；目前已有一些高效的BE方案：如文献[16]中提出的基于多线性映射的高效BE方案，实现了密文大小、公私钥大小等都比较短(对数级大小)、而且也支持基于身份的BE；因此本文BE方案更大意义的在于理论价值：提出了WE的另一个应用——BE的构建，进一步拓展了WE方案的应用领域，未来如果出现高效直接的WE方案构建，本文的理论方案就可应用于实际。

3　安全性证明

定理2基于原WE方案的安全性、DDH假设和ROM模型，上述基于增强WE方案构建的BE方案是IND_CPA安全的。

证明：如果存在能攻破BE方案的IND_CPA敌手A，利用A就可以解决DDH难题。归约如下：

给定一对群元素(G,H)，要判断其是否是 DDH元组，挑战者把(G,H)作为公钥生成上述的 BE方案，并把MPK=(G,H)发给A，交互如下：

1)用户私钥查询：当A发出对标识为ID的用户的私钥查询时，挑战者可按如下方式模拟签名(基于ROM模型及证明的零知识特性)：

挑战者选择随机的s和c，并设置scG′=g G 和，控制随机预言器(random oracle)对查询返回值c，并返回签名。注意即使(G,H)不是DDH元组，此模拟签名仍能通过验证方程，而如果(G,H)是DDH元组，此模拟签名和实际签名的概率分布是一样的。敌手A查询的所有ID都放入集合Q中。

2)挑战阶段：敌手A生成两个长度相同内容不同的消息m0和m1，并发给挑战者，挑战者先把集合Q中的所有ID放入RL中，并随机地选b=0或1，对mb用WE进行加密，所用的NP语言为式(7)中的NP语言。

然后把密文CT发给敌手A。

3)敌手A要根据CT来猜测b=0还是1，根据敌手A回答的正确性，挑战者就能解决DDH问题：如果A回答正确，则(G,H)是DDH元组，上述模拟是完美的，根据A的IND_CPA的定义其成功率较高；而如果A的回答是错误的，则(G,H)不是DDH元组，此时对敌手A来说合法签名是不存在的(因其没有对随机预言器的控制能力)，即上述WE定义中x∉L的情况，根据原WE方案的安全性，A的成功概率是可以被忽略的。

为叙述简单起见，上述的证明只能实现IND_CPA的安全性，在安全性定义的博弈中没有解密的Oracle，但注意上述的理论方案也可以实现IND_CCA的安全性，此时只需要模拟一个解密的Oracle，挑战者拥有对随机预言器的控制能力，对任意ID都能生成合法的“伪造”签名，这个“伪造”签名就是一个合法的NP证据，利用此证据挑战者可对任意的消息进行解密，从而模拟解密Oracle。

4　结 束 语

本文提出了WE一种新的应用，可用于构建可撤销的广播加密方案，所构建的广播加密方案具有非常简单的成员重加入功能；在构建过程中，指出原来的WE方案的安全性定义不够强，没有考虑一种非常重要的情况：即敌手知道x∈L，但没有相关的NP证据，为此提出的一种增强的WE安全性，即“特别公正性”；并基于HSMP和原来的WE方案构建了一个符合此安全性要求的WE方案，并在此增强WE方案的基础之上来构建可撤销的广播加密方案。

本文增强的WE方案构建是基于HSMP问题的，而HSMP问题(如DDH、DLIN等)通常不是NP完全问题，因此不是所有NP问题都能归约到HSMP问题，这可能会限制其应用领域。所以一个重要的公开问题就是如何基于NP完全问题来构建增强的WE方案。

[1]GARG S,GENTRY C,SAHAI A,et al. Witness encryption and its applications[C]//The 45th ACM Symposium on Theory of Computing (STOC 2013). New York,USA: ACM,2013: 467-476.

[2]FIAT A,NAOR M. Broadcast encryption[C]// Advances in Cryptology-CRYPTO’ 93. California,USA: Springer Berlin Heidelberg,1994: 480-491.

[3]DODIS Y,FAZIO N. Public key broadcast encryption for stateless receivers[C]//Digital Rights Management 2002. Washington,USA: Springer,2003: 61-80.

[4]NAOR D,NAOR M,LOTSPIECH J. Revocation and tracing schemes for stateless receivers[C]// Advances in Cryptology-CRYPTO 2001. California,USA: Springer Berlin Heidelberg,2001: 41-62.

[5]GARG S,GENTRY C,HALEVI S. Candidate multilinear maps from ideal lattices[C]//Advances in Cryptology-EUROCRYPT 2013. Athens,Greece: Springer,2013:1-17.

[6]GAREY M,JOHNSON D. Computers and intractability: a guide to the theory of NP-completeness[M]. San Francisco,USA: W. H. Freeman and Co,1979.

[7]GENTRY C,LEWKO A,WATERS B. Witness encryption from instance independent assumptions[C]//Advances in Cryptology-CRYPTO 2014. California,USA: Springer,2014: 426-443.

[8]CORON J,LEPOINT T,TIBOUCHI M. Practical multilinear maps over the integers[C]//Advances in cryptology-CRYPTO 2013. California,USA: Springer,2013: 476-493.

[9]CHEON J,HAN K,LEE C,et al. Cryptanalysis of the multilinear map over the integers[C]//Advances in Cryptology-EUROCRYPT 2015. Sofia,Bulgaria: Springer,2015: 3-12.

[10]DIFFIE W,HELLMAN M. New directions in cryptography[J]. IEEE Transactions on Information Theory 2006,22(6): 644-654.

[11]BONEH D,BOYEN X,SHACHAM H. Short group signatures[C]//Advances in Cryptology-CRYPTO 2004. California,USA: Springer,2004: 41-55.

[12]ESCALA A,HEROLD G,KILTZ E,et al. An algebraic framework for diffie-hellman assumptions[C]//Advances inCryptology-CRYPTO 2013. California,USA: Springer,2013: 129-147.

[13]BELLARE M,ROGAWAY P. Random oracles are practical: a paradigm for designing efficient protocols[C]//ACM Conference on Computer and Communications Security 1993. New York,USA: ACM,1993: 62-73.

[14]FIAT A,SHAMIR A. How to prove yourself: Practical solutions to identification and signature problems[C]// Advances in Cryptology-CRYPTO’ 86. California,USA: Springer,1987: 186-194.

[15]CAMENISCH J,STADLER M. Efficient group signature schemes for large groups[C]//Advances in Cryptology-CRYPTO '97. California,USA: Springer,1997: 410-424.

[16]BONEH D,WATERS B,ZHANDRY M,et al. Low overhead broadcast encryption from multilinear maps[C]// Advances in Cryptology-CRYPTO 2014. California,USA: Springer,2014: 206-223.

编辑叶芳

Construction of Revocable Broadcast Encryption Based on Witness Encryption

GUO Ren1,2,CHEN Fu-ji1,and CHENG Xiao-gang3
(1. School of Economic and Management,Fuzhou UniversityFuzhou350116; 2. College of Business Administration,Huaqiao UniversityQuanzhou Fujian362021; 3. College of Computer Science and Technology,Huaqiao UniversityXiamen Fujian361021)

Witness encryption (WE)is a new type of encryption scheme without key generation.It can be used for construction of many other cryptosystems such as public key encryption,IBE,ABE,etc. A new WE application is presented,i.e.,the construction of revocable broadcast encryption (BE)based on WE. The constructed BE scheme also supports a simple re-membership function,which is suitable for applications like pay-TV etc. In the construction,we also point out that the original security definition of WE is not strong enough. So we strengthen the original WE security definition and construct a WE scheme satisfying this new definition based on the original WE scheme,hard subset membership problem and random oracle model.

broadcast encryption;hard subset membership problem;membership revocation;NP witness encryption

TP309

A

10.3969/j.issn.1001-0548.2016.06.016

2016 − 3 − 14；

2016 − 6 − 16

国家自然科学基金(71271056)，福建省自然科学基金(2016J01336)

郭韧(1975 − )，女，博士生，主要从事信息系统、信息安全方面的研究.