广义Gagola特征标的注记

王慧群,曾吉文

(1.长治学院数学系,山西长治046011;2.厦门大学数学科学学院,福建厦门361005)

广义Gagola特征标的注记

王慧群1,曾吉文2

(1.长治学院数学系,山西长治046011;2.厦门大学数学科学学院,福建厦门361005)

设χ∈Irr(G)是广义Gagola特征标,V(χ)={χ(g)|g∈G}.证明了χ是广义Gagola特征标,当且仅当χ忠实,并且V(χ)恰好有3个Galois-轨道.在此基础上,得到经典Gagola特征标的一个充要条件.

广义Gagola特征标;置换特征标;线性无关

1 主要结果

设G是有限群;Irr(G)表示G的所有不可约复特征标集合;Γ=Gal(Q|G|/Q)为域扩张Q|G|/Q的Galois群,其中Q是有理数域,Q|G|表示Q添加|G|-次本原单位根的代数扩域;其余未指明符号均以文献[1]为准.

设σ∈Γ,g∈G,χ∈Irr(G),如文献[1]第90页所示,令χσ(g)=(χ(g))σ,则χσ∈Irr(G).按此定义,Γ作用在集合Irr(G)上.记该作用下χ所在轨道为χΓ,再记n(χ)为χ的非零点共轭类个数,则有如下不等式成立:

|χΓ|+1≤n(χ).

当特征标χ使得上式等号成立时,由文献[2],称该特征标为广义Gagola特征标.本研究的主要目的是给出广义Gagola特征标的一个等价刻画.

记V(χ)={χ(g)|g∈G},考虑Γ在V(χ)上的自然作用.当χ是非线性不可约特征标时,由Burnside定理,存在g∈G使得χ(g)=0.由此可知V(χ)至少有两个不动点χ(1)和0.更进一步,V(χ)至少有3个Γ-轨道.Zhmud[3]研究了当V(χ)恰好是3个Γ-轨道时的有限群.本研究将证明,此时的特征标恰好是广义Gagola特征标.

本研究的主要结论为如下定理.

定理1 设G是有限非交换群,符号Γ,V(χ)及Irr(G)如上,则χ是广义Gagola特征标当且仅当χ忠实,且V(χ)恰好有3个Γ-轨道.

根据定理1,可得如下推论.

推论1 条件如定理1,则χ是Gagola特征标当且仅当χ忠实,且|V(χ)|=3.

推论1必要性中的Gagola特征标最初出现在文献[4],即满足n(χ)=2的不可约特征标.对于充分性中的条件|V(χ)|=3,也是经典情形,具体见文献[5].

2 知识准备

以下罗列的定义,术语和结论,仅为阅读方便.

定义1 符号如上,称χ为广义Gagola特征标,如果

|χΓ|+1=n(χ).

根据文献[2],当χ是广义Gagola特征标时,χΓ的所有成员都是广义Gagola特征标,并且都是忠实的.

证明定理1之前,还需要如下的一个初等事实.

引理1 设B=(aij)是秩为r-1的(r-1)×r矩阵.如果B中每行元素和均为0,则B中任意r-1个列向量均线性无关.

3 定理证明

本部分内容主要是定理1的证明,另外也包含推论1的证明.

以下是定理1的证明.

证明 (i)先证明定理的必要性,即先假定χ是广义Gagola特征标.

由文献[2],广义Gagola特征标χ是忠实特征标.

记χ的非零点共轭类为C1=1,C2,…,Cr.设nj为Cj的代表元,其中j=1,2,…,r.令aj=χ(nj),则V(χ)={χ(1)=a1,a2,…,ar,0}.因为χ(1)和0都是Γ-不动点,为完成必要性证明,只需证明a2,…,ar恰是一个Γ-轨道.记U={a2,…,ar},则Γ可以作用在U上,以下证明Γ在U上是传递作用.

由广义Gagola特征标的定义,可设χ的Γ-轨道χΓ={χ1=χ,χ2,…,χr-1}.记W=χΓ,定义

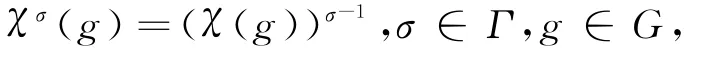
则Γ可以作用在W上,并且是传递的.

设X是特征标表所确定的矩阵.在X中,选取χ1, χ2,…,χr-1所在行,C2,…,Cr所在列的r-1阶子矩阵A=(cik),其中cik=χi(nk+1).考虑Γ在上述两个集合U和W的作用,只要A可逆,模仿文献[1]定理6.32的证明,就能得到两个作用的置换特征标相同.再由文献[1]推论5.15,可知两个作用的轨道数相同.而Γ在W上是传递作用,故在U上也是传递作用.为此,需验证A是可逆矩阵.

在特征标表X中,由χ1,χ2,…,χr-1所在行,C1=1,C2,…,Cr所在列确定的子矩阵记为(cij)(r-1)×r,其中cij=χi(nj).由于X可逆,可知该矩阵的秩为r -1.令B=(|Cj|cij),可知B的秩也是r-1.考察以B为系数矩阵的齐次线性方程组,可知该方程组的基础解系仅含一个解.注意到主特征标1和χ的内积[1,χi]=0,可知(1,1,…,1)′即为基础解系.换言之, B满足引理2的条件,因此任意B的任意r-1列都是线性无关的.特别地,B划去第一列所得子矩阵是可逆的,从而得到A可逆.

(ii)再证充分性,即假定χ忠实,且V(χ)恰好有3个Γ-轨道.

设V(χ)的3个Γ-轨道为χ(1),0,{a2,a3,…, ar}.记Cj={g∈G|χ(g)=aj},由文献[3]结论1,可知Cj恰是G的共轭类,即得n(χ)=r.

又因为a2,a3,…,ar是r-1个互不相同的数,可知|χΓ|≥r-1,迫使|χΓ|+1=r=n(χ),故χ是广义Gagola特征标.

以下是推论1的证明.

证明 如果χ是Gagola特征标,由文献[4]可知χ忠实且|V(χ)|=3.反之,如果χ忠实且|V(χ)|= 3,记V(χ)={χ(1),0,a}.再记C={g∈G|χ(g)= a}.重复上述充分性的证明过程,可知n(χ)=2,也即χ是Gagola特征标.

[1] ISAACS I M.Character theory of finite groups[M].New York:Academic Press,1976:90.

[2] WANG H Q,CHANG Xuewu,JIN Ping.On generalized Gagola characters[J].Arch Math,2015,104:501-508.

[3] ZHMUD E.Finite groups possessing a faithful nonlinear irreducible character with three classer of algebraically conjugate values[J].Journal of Algebra,2000,226: 225-235.

[4] GAGOLA S M.Characters vanishing on all but two conjugacy classes[J].Pac J Math,1983,109:363-385.

[5] BERKOVICH Y,CHILLAG D,ZHMUD E.Finite groups in which all nonlinear irreducible characters have three values[J].Houston J Math,1995,21(1):17-28.

[6] LEWIS M L.Bounding fitting heights of character degree graphs[J].Journal of Algebra,2001,242:810-818.

A Note on Generalized Gagola Characters

WANG Huiqun1,ZENG Jiwen2

(1.Department of Mathematics,Changzhi Collage,Changzhi 046011,China; 2.School of Mathematical Science,Xiamen University,Xiamen 361005,China)

Let G be a finite group,χ∈Irr(G)be a generalized Gagola character,and V(χ)={χ(g)|g∈G}.This note gives a necessary and sufficient condition for the generalized Gagola character,and it is also proved thatχis a generalized Gagola Character if and only ifχis faithful and|V(χ)|=3.

generalized Gagola characters;permutation character;linear independence

O 152

A

0438-0479(2016)06-0927-02

10.6043/j.issn.0438-0479.201509018

2015-09-18 录用日期:2015-12-24

国家自然科学基金(11261060)

jwzeng@xmu.edu.cn

王慧群,曾吉文.广义Gagola特征标的注记[J].厦门大学学报(自然科学版),2016,55(6):927-928.

WANG H Q,ZENG J W.A note on generalized Gagola characters[J].Journal of Xiamen University(Natural Science), 2016,55(6):927-928.(in Chinese)