适用于W波段ISAR成像的二维补偿方法

魏一搏,王 辉,李 宁,禹卫东

(1.中国科学院电子学研究所,北京 100190; 2.中国科学院大学,北京 100039)

适用于W波段ISAR成像的二维补偿方法

魏一搏1,2,王 辉1,李 宁1,2,禹卫东1

(1.中国科学院电子学研究所,北京 100190; 2.中国科学院大学,北京 100039)

针对W波段逆合成孔径雷达成像过程中越分辨单元徙动严重的问题,提出了一种二维补偿成像方法.该方法首先分析了逆合成孔径雷达成像中目标徙动产生的原因,然后使用Keystone变换对距离向徙动进行补偿;对于均匀转速目标,使用最小熵法从方位向徙动中估计目标的平均转动角速度,用相位补偿的方法对均匀角速度目标的方位向徙动进行补偿;最后,对于变化角速度目标,利用子孔径的方法降低目标成像中的由角速度变化带来的方位向徙动.该方法在仿真中获得了高分辨率的成像结果,证明了该算法的有效性.

W波段;逆合成孔径雷达;Keystone变换;相位补偿;子孔径成像

逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)是一种高分辨率微波成像系统,它能够提供空中、地面以及太空目标的二维成像结果[1].近年来,随着针对W波段研究的深入以及W波段元器件的发展,W波段引起了世界各国尤其是发达国家的重视[2-3].W波段众多的优越特性,使得W波段ISAR技术有巨大的应用前景.在成像中,相比传统波段,W波段可以获得厘米级的分辨率,使系统获得更多的目标细节,提高对目标的判别准确率.

基于W波段的ISAR系统,笔者针对成像过程中的徙动影响,建立了转动目标的ISAR回波相位模型.采用Keystone算法[4]进行距离向的徙动补偿.对方位向的徙动,利用最小熵的方法估计得到转动的角速度.在此基础上实现了方位向徙动的补偿.对于转动速度变化的目标,使用了子孔径方法进行成像.最后进行了仿真验证.

1　ISAR成像模型

随着W波段分辨率的提高,对于ISAR处理的补偿精度要求进一步提高.ISAR的补偿可以分为运动补偿和徙动补偿两部分.运动补偿是在对机动目标成像过程中产生的,对于机动目标,需要对其在成像干涉过程中目标中心点的距离向移动进行补偿,使其等效于在同一个距离位置上进行自旋转动,以完成之后的成像处理.关于ISAR成像的运动补偿在传统波段已经有了较为深入的研究,有许多成熟的算法[5-6],这些方法可以适用到W波段的成像处理中,因此笔者认为输入信号是经过运动补偿后的信号.

这里根据文献[2-3]中的系统参数,假设W波段的ISAR成像系统分辨率为3 cm,则可以得到成像总转角为0.05 rad.假设目标尺寸25 m,则可以得到一阶至三阶的徙动分别约为1.25 m,3.12 cm以及5.2 mm.由此可以看出,在W波段ISAR成像中,徙动量比分辨率大许多,需要进行补偿处理才能得到较好的成像结果.同时进行回波计算时,采用二阶的近似处理较为合理.

考虑只绕中心点进行转动的目标,处理由于目标转动带来的越分辨单元徙动所产生的图像散焦问题.目标与雷达的关系如图1所示.

图1　ISAR成像几何关系图

雷达所能获得的信息就是目标上的点与雷达的距离R所带来的回波时延信息.假设雷达与目标中心点O的距离为R0,目标上有一坐标为(A,R)的点,当目标转动角度为θ时,采用fc+f的线性调频信号,假设目标以恒定的角速度ω转动时,回波的相位信息为

通过匹配滤波,由相位的第1项可以得到目标点的距离向坐标.通过方位向的快速傅里叶变换(Fast Fourier Transform,FFT),由式(1)的第2项,可以得到方位向的相对位置.式(1)的第1项和第4项则为目标转动所带来的距离向与方位向的越分辨单元徙动.如果不补偿后两项,则会造成成像结果的模糊.

2　W波段成像特点及现有成像处理方法

W波段由于分辨率高、分辨单元小,所以越分辨单元的徙动问题比传统波段要严重得多;同时随着成像分辨率的提升,W波段图像的数据量也比传统波段大了许多.如果成像所使用算法的计算复杂度较高,会带来计算时间的较大幅度增加.所以需要对成像算法的计算复杂度进行考虑.

在现有的成像处理方法中,比较成熟的主要有距离多普勒(Range Doppler,RD)算法[1]、Keystone变换[4]、极坐标格式算法(Polar Formation Algorithm,PFA)[7]、后向投影(Back Projection,BP)算法[8]、时频方法[9]、运动参数估计法[10-11]等.但RD算法是不进行补偿,直接成像的方法,成像结果较差;Keystone算法能够较好得补偿目标距离向的徙动,但并没有处理方位向的徙动;PFA算法和BP算法需要得到目标较为准确的角速度才能成像,且算法的复杂度较高,耗时很长;时频方法将目标在方位向进行时频分析,能够减轻方位向的徙动,但会带来方位向分辨率的严重下降;低阶的运动参数估计方法[10]只能够对转动速度稳定的目标进行补偿,而高阶的运动参数估计方法[11]具有较高的运算复杂度.

3　二维补偿成像处理

针对W波段成像的特点,文中提出了一种在距离向与方位向分别进行二维越分辨单元徙动(Migration Through Resolution Cell,MTRC)补偿的成像方法.在距离向使用Keystone变换补偿徙动,在方位向使用最小熵角速度估计与相位补偿、子孔径法相结合的方法进行补偿.该方法能够在W波段得到较好的成像结果,同时该算法的运算复杂度较低,计算所需时间较短.

3.1距离向MTRC补偿

距离向MTRC可以利用Keystone方法进行补偿.Keystone变换是通过对回波信号在频率域时间轴上的变标操作来实现对距离向徙动的补偿的.针对式(1),将tk=t(f+fc)/f带入,得到

即补偿了第3项的距离向徙动.

3.2均匀角速度目标的方位向MTRC补偿

为了进行方位向的徙动补偿,可以进一步展开式(2)中的最后一项,将tk=ak/fPRF,R=ρRr,ρR=c/2B带入.其中的ak,r,ρr分别是图像在Keystone变换后的方位向点数、距离向点数以及距离向的分辨率.fPRF为脉冲重复频率(Pulse Repetition Frequency,PRF).可以得到

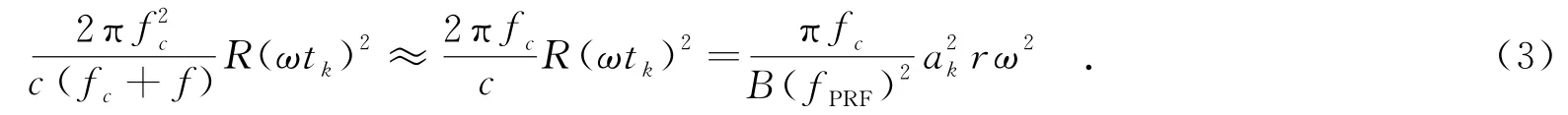
这里假设发射信号的相对带宽较小,可以忽略.通过式(3)可以看出,方位向的徙动带来的相位差在图像的某一点上,是只与目标的转动速度有关的函数,因此这里可以采用假定不同的转动角速度,得到成像结果,再利用最小熵搜索的方法来估计目标的转动角速度.在搜索的过程中,可以采用多次搜索,并逐次递增搜索精度的方法来降低计算量.角速度搜索的最大精度正比于成像结果的分辨率.在估计得到目标的转动角速度后,给图像上的每个点叠加由式(3)计算得到的相位,即可补偿方位向的MTRC.

3.3均匀角速度目标方位向MTRC补偿误差分析

假设角速度的估计有Δω的误差,忽略信号相对带宽以及Keystone变化对时间维造成的影响,由此,可得对方位向造成误差的相位,即

其中,τ为成像时间,这里假设Δω相对ω为小量.

相位误差在成像后造成的目标点偏移为

其中,N为成像中方位向的总点数.

由此可以看出,这一偏移是随着目标距离向离转动中心距离的增大而增大的,同时是随着时间增大的.假设在经过最小熵的搜索过程后,ΔN对于最大的偏移能够达到最高的1/2格数补偿精度.则角速度估计的误差为

其中,RT为目标距离向与转动中心的最大距离.

从式(6)可以看出,在W波段的成像中,较大的方位向MTRC为角速度的估计带来了较高的精度.

3.4变化角速度目标的方位向MTRC补偿

以上所讨论的都是基于目标角速度不变的情况,然而在实际的应用中,大部分目标的角速度都会发生不同程度的变化,因此,需要考虑目标角速度变化对结果带来的影响.

假设角度随时间变化的函数为ω(t),先对变化角速度的目标进行上文所述的均匀角速度目标的补偿处理.根据上文方法估计得到的平均角速度为可以得到在(A,R)点,由于角速度变化所造成的相位误差为

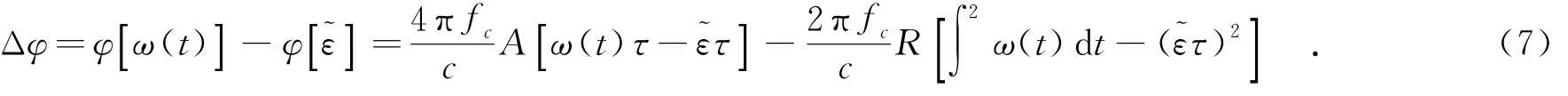
式(7)中的前一项代表着目标角速度变化所造成的方位向的偏移,需要进一步的补偿.而如果能够较为准确得估计得到目标角速度的平均值,则式(7)中后一项可以被之前所进行的相位补偿处理所补偿.

如果目标的角速度为ω(t),则在每个慢时间点,目标的方位向坐标点为

从式(8)中可以看出,目标的成像点会由于角速度的变化,随着时间移动.同时这一偏移是随着方位向的增大而增大的,在图像的中心点,偏移为零.

由于目标的角速度随着时间变化,在整个合成孔径时间内,目标在方位向会不断进行偏移.这里假设目标的角速度是连续的,则在一小段时间内,目标的角速度变化会较小,即如果只对一小段孔径进行成像,则目标在方位向由于角速度变化所带来的徙动也会较小.由此可以通过将回波数据分成若干个子孔径分别进行成像,用再合成的方法来降低角速度变化带来的方位向徙动.假设第K个子孔径的平均角速度为,可以得到目标上的(A,R)点方位向坐标为

从式(10)可以看出,只需要对各子孔径图像进行方位向的伸缩处理就可以得到各目标点坐标完全一致的子图像.得到子图像后只需将各子图像转换回时域,叠加后再重新成像即可得到合成的图像.通过子孔径的处理可以有效地降低角速度变化所带来的影响.同时由于子孔径方法充分利用了各子孔径的信息进行相干叠加,图像的分辨率与原图像的相同.

在实际的处理过程中,由于各子孔径平均角速度的估计误差较大,可以采用选取某个子孔径为基准,对其他子孔径进行对齐的方法进行.为了获得某个子孔径相对基准孔径的伸缩倍数,可以设置不同的伸缩倍数,对两个孔径进行合成成像,根据所得图像的熵进行搜索的方法进行.

通过使用子孔径的方法,可以降低目标角速度变化所带来的方位向徙动.这种方法可以适用于一定幅度内任意变化的角速度.并且这种方法是由成像结果进行参数的选取,具有较强的抗干扰性能.这种方法在每次的搜索过程中,只需要对子孔径进行方位向的傅里叶变换以及伸缩处理.伸缩处理可以使用基于Chirp-Z变换的方法实现,因此每次搜索的运算复杂度较低、耗时较少.

4　仿真验证与分析

4.1均匀角速度目标成像

由于W波段设备的成像数据现阶段较难获得,因此文中采用了仿真的方式来验证算法的正确性.所采用的系统参数如表1所示.

表1　系统仿真参数列表

使用RD成像算法得到的结果如图2(a)所示.距离压缩后,使用Keystone方法进行了距离向补偿得到的结果如图2(b)所示,利用角速度搜索结果进行相位补偿后的成像结果如图2(c)所示.可以看出对于均匀转速的目标,已经完全补偿了目标的徙动,得到了清晰的图像.

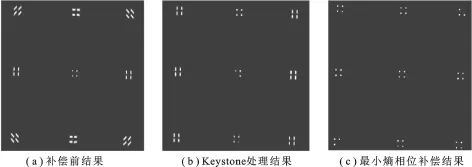
图2　均匀角速度目标二维补偿效果图

4.2变化角速度目标成像

当目标的角速度发生变化时,会造成额外的多普勒频率变化,继而引起方位向的成像位置移动,引起成像的方位向模糊.仿真中除目标角速度外,均采用表1中所示的参数.设置目标的角速度具有二阶以及三阶的角加速度.

使用均匀角速度成像算法得到的结果如图3(a)所示.将得到的结果分成4个子孔径进行处理,经过搜索以及进一步补偿成像后,得到的结果如图3(b)所示.从图中可以看出,成像质量虽然比没有角加速度时的图2(c)有一定的下降,但与图3(a)相比,降低了角加速度所带来的方位向模糊,得到了较好的成像结果.

图3　子孔径补偿效果图

4.3算法耗时

文中仿真计算处理的场景总点数为1 000×1 000,使用的是Core i7-2670 QM 2.2 GHz处理器.这里列出了对于变化角速度目标计算过程的耗时.算法各部分的计算时间如表2所示.

表2　各模块计算时间s

从表2中可以看出,对于这一尺寸的场景来说,算法的总耗时是可以接受的.

5　结束语

笔者研究了W波段ISAR越分辨单元徙动的产生原因,以及针对均匀角速度和变化角速度目标的补偿方法.在此基础上进行了成像,并进行了仿真验证.研究表明:对于W波段的ISAR成像,距离向的徙动可以通过Keystone算法进行补偿.对于均匀转速的目标,方位向的徙动可以通过最小熵相位补偿方法进行补偿,在W波段下,补偿的误差较小.对于转速变化的目标,使用子孔径与相位补偿相结合的方法可以得到较好的成像结果.与此同时,文中所提出的算法具有较低的运算复杂度,耗时较少.

[1]AUSHERMAN D A,KOZMA A,WALKER J L,et al.Developments in Radar Imaging[J].IEEE Transactions on Aerospace and Electronic Systems,1984,20(4):363-400.

[2]LINCOLN LABORATORY.MIT Lincoln Laboratory 2009 Annual Report 2009[EB/OL].[2015-1-12].http://www. ll.mit.edu/publications/Annual̠Report̠2009.pdf.

[3]DANLY B G,CHEUN J,GREGERS-HANSEN V.WARLOC:a High-power Millimeter-wave Radar[C]//Proceedings of Twenty Seventh International Conference on Infrared and Millimeter Waves.Piscataway:IEEE,2002:233-234.

[4]陈文驰,保铮,邢孟道,等.基于Keystone变换的低信噪比ISAR成像[J].西安电子科技大学学报,2003,30(2): 155-159. CHEN Wenchi,BAO Zheng,XING Mengdao,et al.Keystone Transformation Based ISAR Imaging at the Low SNR Level[J].Journal of Xidian University,2003,30(2):155-159.

[5]黄大荣,张磊,邢孟道,等.机动目标ISAR自聚焦新方法[J].西安电子科技大学学报,2014,41(3):71-78. HUANG Darong,ZHANG Lei,XING Mengdao,et al.Autofocus Method for Maneuvering Targets[J].Journal of Xidian University,2014,41(3):71-78.

[6]YU X,ZHU D Y,ZHANG J D,et al.Motion Compensation Algorithm Based on the Designing Structured Gram Matrices Method[J].IET Radar,Sonar&Navigation,2014,8(3):209-219.

[7]WALKER J L.Range-Doppler Imaging of Rotating Objects[J].IEEE Transactions on Aerospace and Electronic Systems,1980,16(1):23-52.

[8]MENSA D L,HALEVY S,WADE G.Coherent Doppler Tomography for Microwave Imaging[J].Proceedings of the IEEE,1983,71(2):254-261.

[9]李亚超,苏军海,邢孟道,等.利用时间-调频率分布特性的复杂运动目标ISAR成像研究[J].西安电子科技大学学报,2008,35(1):1-7. LI Yachao,SU Junhai,XING Mengdao,et al.Research on ISAR Imaging of the Complexly Moving Target Based on the Time-chirp Distribution[J].Journal of Xidian University,2008,35(1):1-7.

[10]XU Z W,ZHANG L,XING M D,et al.Uniform Rotational Motion Compensation for Inverse Synthetic Aperture Radar Targets from Image Domain[C]//IEEE China Summit and International Conference on Signal and Information Processing Conference.Piscataway:IEEE,2014:166-170.

[11]LI Y C,XING M D,SU J H,et al.A New Algorithm of ISAR Imaging for Maneuvering Targets with Low SNR[J]. IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):543-557.

(编辑:王 瑞)

Two dimension migration compensation method for W-band ISAR imaging

WEI Yibo1,2,WANG Hui1,LI Ning1,2,YU Weidong1
(1.Institute of Electronics,Chinese Academy of Sciences,Beijing 100190,China; 2.University of Chinese Academy of Sciences,Beijing 100039,China)

The problem of migration through the resolution cell(MTRC)in the W-band Inverse Synthetic Aperture radar(ISAR)imaging system is serious.Therefore,a novel two dimensional compensation method is proposed in this paper.Firstly,the cause of migration in ISAR imaging is analyzed.Then,the Keystone transform is used to compensate the MTRC in the range direction.After that,the minimum entropy algorithm is used to estimate the average rotate speed of the target and the rotate speed is used to compensate the cross range direction MTRC of a uniformly rotating target by using the phase correcting method.Finally,the sub-aperture imaging algorithm is used to reduce the cross range MTRC in imaging the maneuvering target.Simulation results show that a high resolution result is achieved and the effectiveness of the two dimensional compensation method is verified.

W-band;ISAR;keystone transform;phase correction;sub-aperture imaging

TN955+.1

A

1001-2400(2016)03-0155-06

10.3969/j.issn.1001-2400.2016.03.027

2015-01-19

时间:2015-07-27

魏一搏(1990-),男,中国科学院电子学研究所硕士研究生,E-mail:ghost200802@163.com.

王 辉(1972-),女,副研究员,E-mail:wanghui@mail.ie.ac.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20150727.1952.027.html