变转速下滚动轴承阶比峭度图法故障特征提取
2016-12-07徐冠基
柏 林, 甄 杰, 彭 畅, 徐冠基
(重庆大学机械传动国家重点实验室 重庆,400044)
变转速下滚动轴承阶比峭度图法故障特征提取
柏 林, 甄 杰, 彭 畅, 徐冠基
(重庆大学机械传动国家重点实验室 重庆,400044)
结合传统阶比分析和峭度图算法的优势,利用计算阶比跟踪方法将时域非平稳信号转换为角域平稳信号,并利用峭度指标准确表征滚动轴承振动信号中的故障瞬态冲击大小,提出了阶比峭度图算法。仿真故障信号及实测滚动轴承外圈故障信号分析结果表明,阶比峭度图算法能够有效识别阶比域内的最优包络解调频带参数,显著提高了变转速工况下滚动轴承故障特征提取的准确性。
滚动轴承; 变转速; 阶比谱; 阶比峭度图
引 言
滚动轴承是旋转机械中应用最广泛的机械部件,其运行状态直接影响整个机器的性能。存在局部缺陷的滚动轴承在运行时将产生包含脉冲冲击的非平稳振动信号,如何从这些非平稳振动信号中提取故障信息成为滚动轴承故障诊断的关键[1]。自Pearson[2]率先提出峭度的概念并用于衡量样本分布偏离正态分布的程度之后,峭度统计量在概率论与数理统计领域得到了广泛研究。Dyer等[3]将峭度指标引入机械工程领域中,用于衡量机械故障严重程度。由于峭度能够准确表征滚动轴承振动信号中故障瞬态冲击大小,其相关研究在滚动轴承故障振动领域得到了充分发展。Dwyer[4]定义了谱峭度的概念以描述信号频谱幅值峭度值。尽管平稳信号的谱峭度理论发展迅速,而非平稳信号的谱峭度一直没有正式定义,直到Antoni[5]基于Wold-Cramér分解理论正式定义了条件非平稳过程的谱峭度系数,才奠定了谱峭度在非平稳信号分析中的理论基础。Antoni提出了基于短时傅里叶变换(short-time Fourier transform,简称STFT)的谱峭度算法[6]和基于二进有限长度单位冲激响应(finite impulse response,简称FIR)滤波器组的快速峭度图算法[7]。由于传统谱峭度算法不能有效处理变速振动信号,因此有必要采取手段消除转速波动的影响。阶比分析作为一种提取振动信号中与转速密切相关成分的方法,其核心是将时域非平稳信号通过等角度采样的方式转换为角域平稳信号,然后对角域信号进行快速傅里叶变换获取阶比谱[8]。
笔者将阶比分析技术嵌入到传统峭度图算法中,提出了阶比峭度图算法,将其成功用于分析变转速下的仿真轴承故障信号和实测轴承外圈故障信号。
1 理论介绍
1.1 谱峭度
(1)
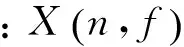
基于四阶距累积量的谱峭度可定义为
(2)

当冲击故障信号中存在平稳高斯噪声时,谱峭度可以定义为
(3)
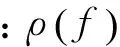
1.2 基于FIR滤波器的峭度图
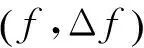
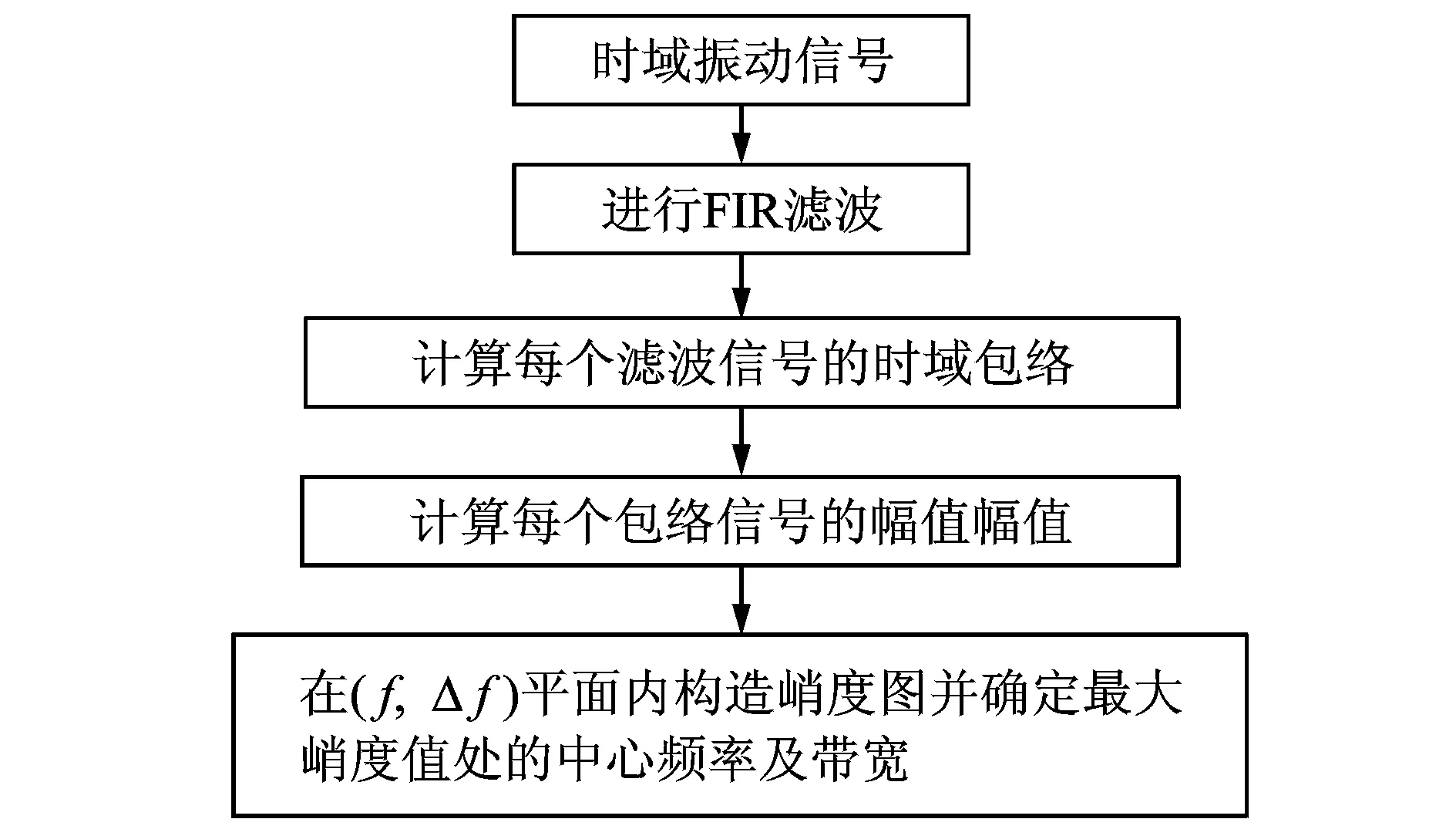
图1 基于FIR滤波器的峭度图流程Fig.1 Flow chart of FIR filter-bank based kurtogram
1.3 计算阶比跟踪法
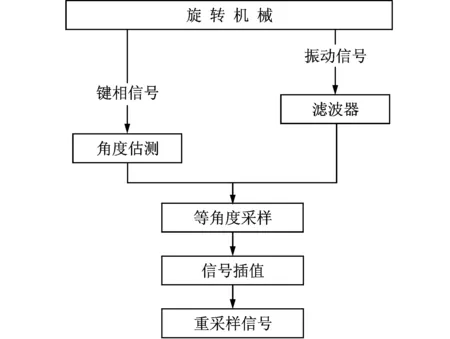
图2 计算阶比跟踪原理Fig.2 Principle of COT
振动信号和转速信号在相同的时间间隔被异步采样,然后通过数字信号处理算法用软件的形式合成同步采样振动数据,这个过程就是计算阶比跟踪(computed order tracking,简称COT)法。与传统的阶比跟踪方法相比,COT不仅具有更高的精度且无需特定的硬件,更适用于旋转机械实际状态监测[9]。COT系统通常基于3个模块:转速脉冲触发器模块、角度估算模块和信号插值模块。如图2所示,具体步骤为:a.对原始振动信号和键相信号分两路同时进行等间隔采样,得到异步采样信号;b.通过采集的键相脉冲序列(通常是每转一个脉冲)进行转速估计,并作为振动相角的测量基准;c.利用转速估计得到等角度采样发生的时刻序列;d.在等角度采样发生时刻附近时间区间内异步采样振动信号并进行插值计算,通过重采样生成同步采样信号。
2 阶比峭度图算法
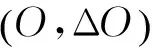
(4)
其中:待定系数b0,b1,b2通过求解3个连续时刻t0,t1,t2下的转角线性方程组(5)得到。
(5)
将求解的待定系数代入式(4),得到时域信号重采样过程中的等角度采样时标
(6)
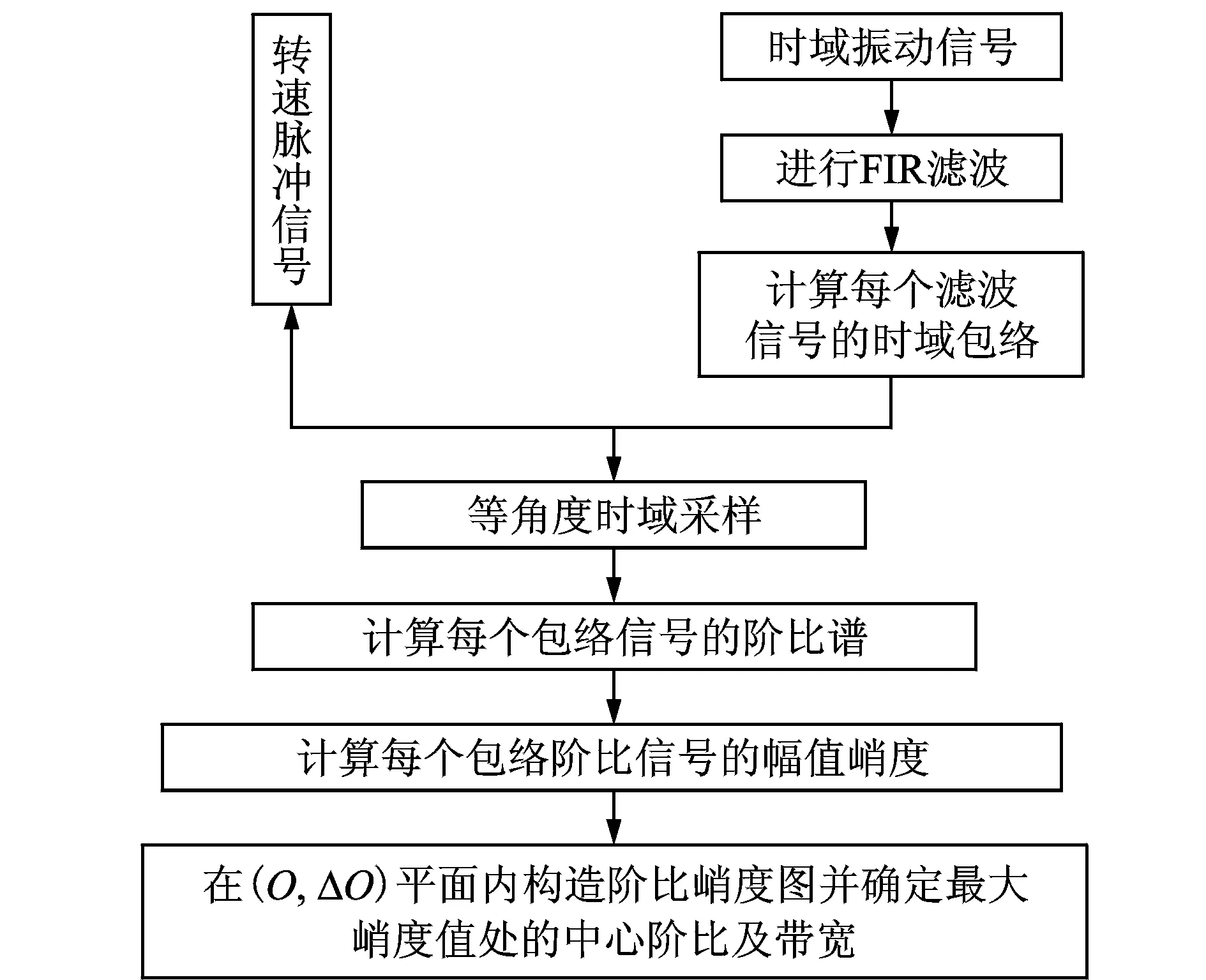
图3 阶比峭度图流程Fig.3 Flow of COT-kurtogram
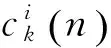
(7)
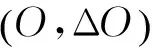
有别于文献[10]中计算各包络信号的频谱幅值峭度分布,然后再计算最优包络信号的阶比谱,笔者计算了各包络信号的阶比谱幅值峭度分布图,并在得到最优解调阶比带参数后直接反求,得到此参数对应的最优的阶比谱。这样可提高变转速下滚动轴承故障特征提取的准确性。
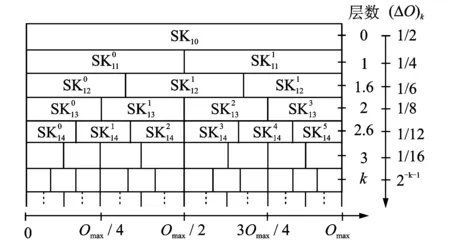
图4 基于FIR滤波器的阶比峭度图Fig.4 The FIR filter-bank based COT-kurtogram
3 仿真实验分析
为了验证阶比峭度图算法的有效性,进行变转速下仿真实验。仿真信号的转速频率f(t)=2t Hz,主轴转速n(t)=60f(t)r/min,仿真一个阶数分别为1阶、2阶和3阶的升速强低频干扰信号y(t),y(t)=sin(2πt2)+0.6sin(4πt2)+0.3sin(6πt2)。仿真一个每转内5阶的故障振动信号R(t),R(t)=eaT1sin(2πfct),T1=mod(t,1/fd),fd=5t,其中:a=300,fc=4 kHz。仿真一个高斯白噪声干扰信号w(t),仿真的轴承故障振动信号模型(取t=9~10 s段)为
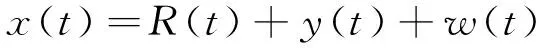
(8)
仿真中取采样频率fs=25 kHz,仿真的滚动轴承时域振动信号如图5所示。由于受噪声干扰,瞬态冲击成分在整个信号中并不明显。直接对原始仿真信号进行阶比跟踪得到的阶比谱如图6所示。图中只有仿真的强低频干扰信号y(t)的阶比,而没有发现仿真的故障振动信号R(t)的阶比。这说明故障振动信号非常微弱,被强低频干扰信号所淹没。
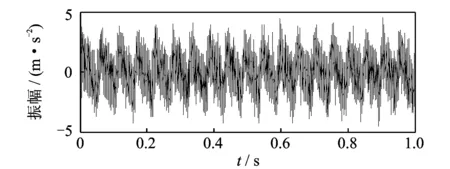
图5 滚动轴承仿真振动信号Fig.5 Simulated vibration signal rolling elements bearing
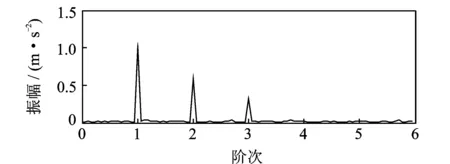
图6 未经阶比峭度图分析的仿真信号阶比谱Fig.6 Order spectrum of simulated signal without COT-kurtogram analysis
依据基于FIR滤波器的阶比峭度图算法,计算了滚动轴承故障仿真信号的基于峭度系数SK1以及FIR滤波器的阶比峭度图,如图7所示。图7为第4.5分解层上阶比谱峭度最大值SK1max=96.2处(图中虚线框标示处)所在中心阶比Oc=8.75,阶比带宽为Bw=1.166 7,此参数即为最优共振解调参数。对应的阶比谱即为所求最优阶比谱,如图8所示。相对于图6,图8所示的经过阶比峭度图分析后的仿真信号阶比谱可清晰地看到仿真的5阶故障特征阶比及其倍频。这说明强低频干扰被抑制甚至被去除,微弱故障特征被有效地提取出来,从而验证了阶比峭度图算法的可行性。
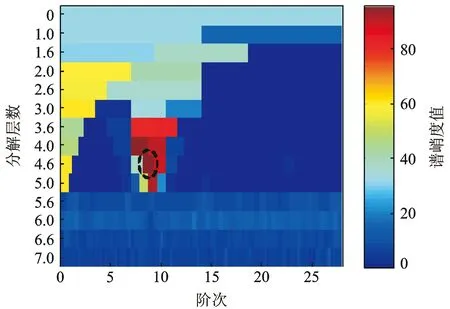
图7 仿真信号的阶比谱峭度图Fig.7 COT-kurtogram of the simulated signal
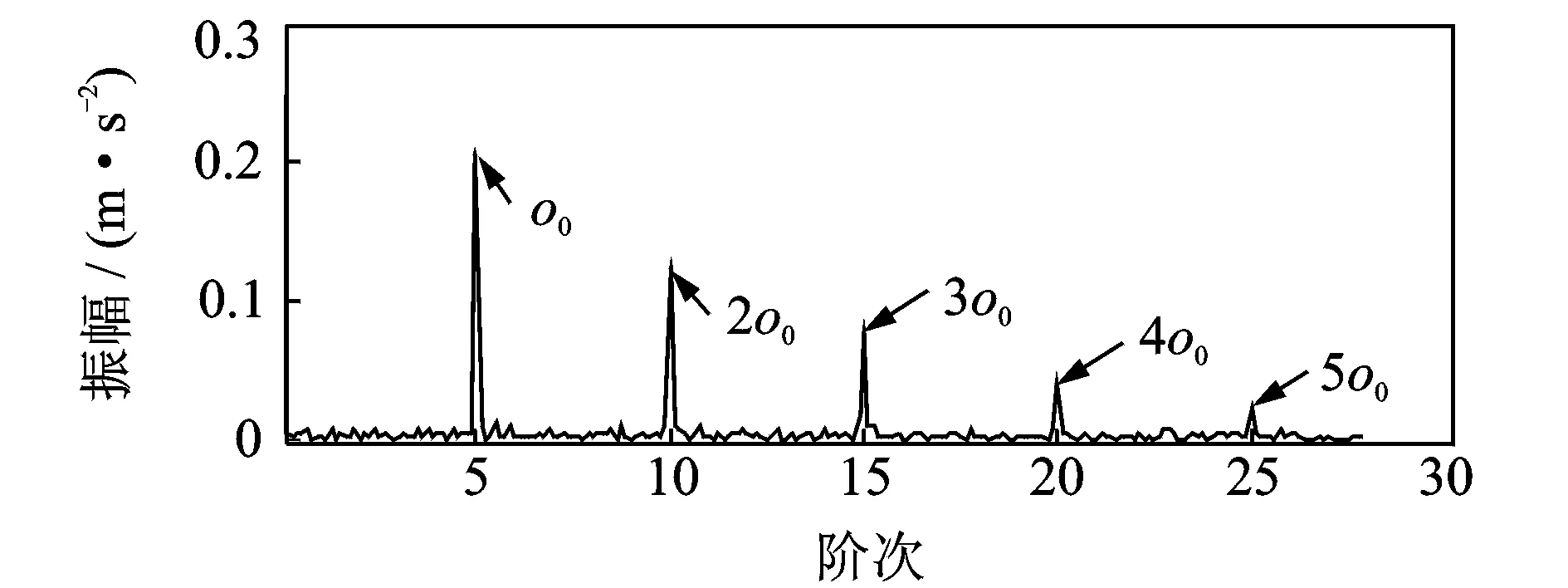
图8 阶比峭度图分析后的仿真信号阶比谱Fig.8 Order spectrum of simulated signal with with COT-kurtogram analysis
为了验证本算法对速度小范围波动的适应性及不同加速度情况下的适应性,笔者对另一组有波动的仿真信号进行了仿真实验。转速频率f(t)=(t+cos(10t)/10)Hz;以与第1组仿真信号相同的方法仿真一个阶数分别为1阶、2阶、3阶的强低频干扰信号y(t),再仿真一个每转内4阶的故障振动信号R(t),最后仿真一个高斯白噪声干扰信号w(t)。仿真的轴承故障振动信号模型为x(t)=R(t)+y(t)+w(t) ,仿真中同样取采样频率fs=25 kHz。
带有速度波动的仿真信号速度模型(18~23 s)如图9所示。仿真的滚动轴承时域振动信号(取20~21 s之间的一段)如图10所示。
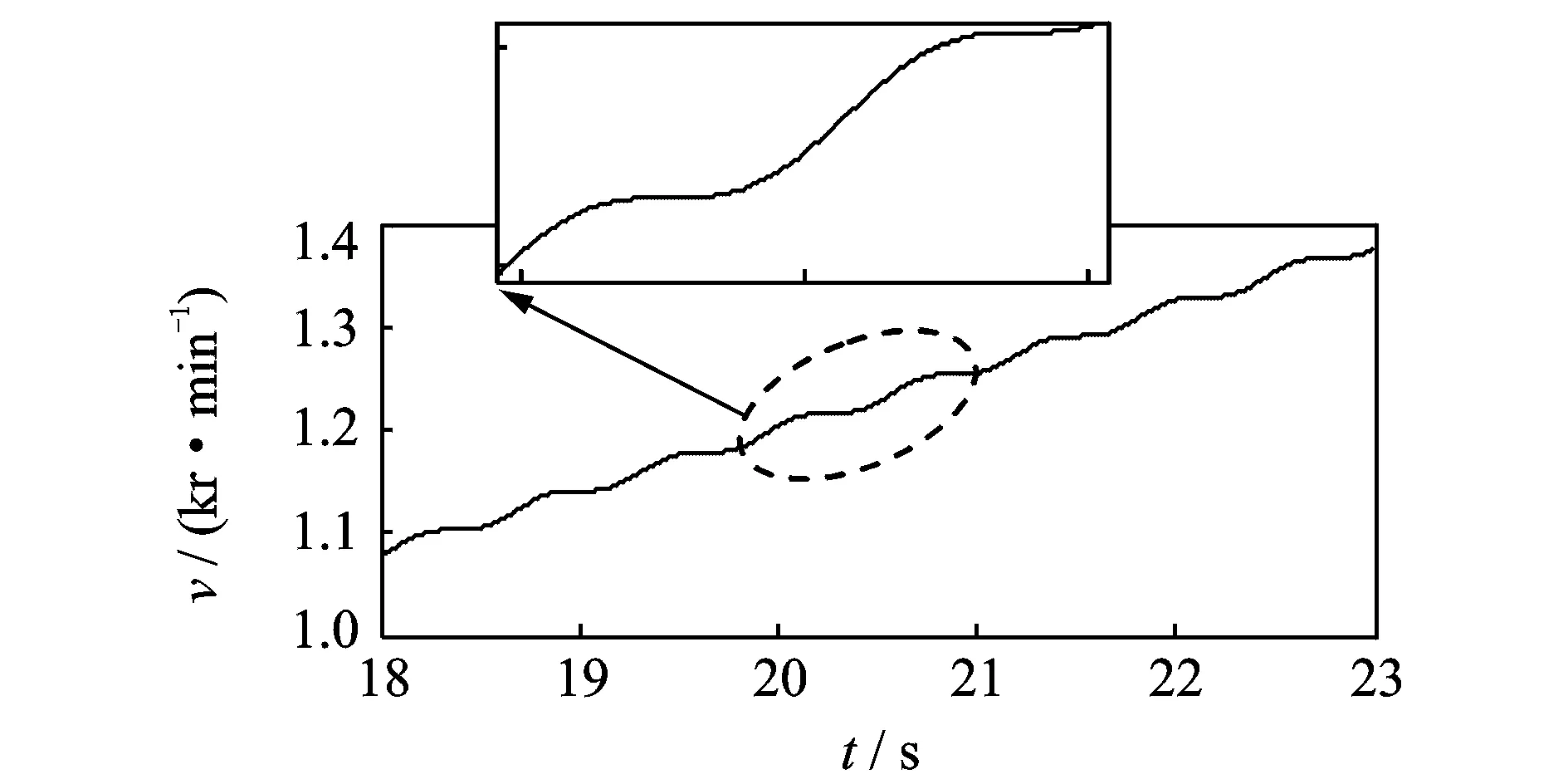
图9 有波动的仿真信号速度模型Fig.9 Simulated velocity model with fluctuation
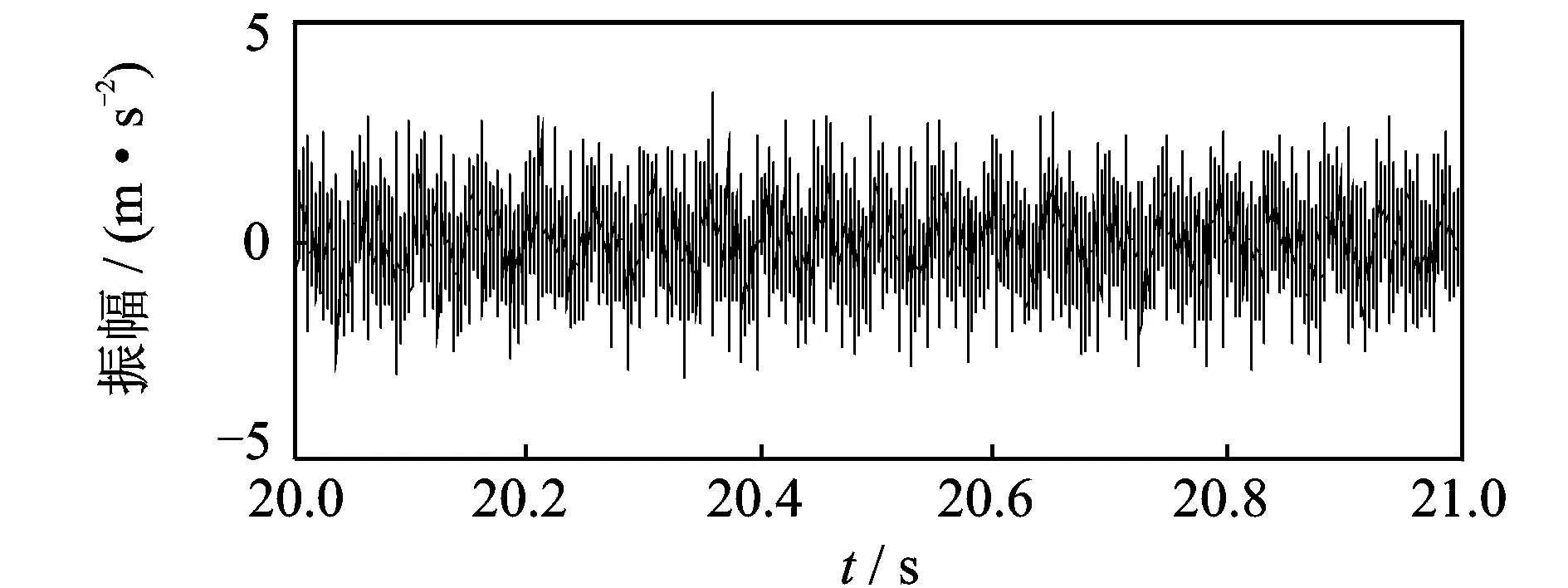
图10 滚动轴承仿真振动信号Fig.10 Simulated vibration signal rolling elements bearing
对仿真的滚动轴承振动信号进行阶比峭度图计算,得到仿真信号的阶比峭度图,如图11所示。在中心阶比为Oc=10.56,阶比带宽为Bw=7,分解层数在2层上进行最优解调得出最优阶比谱,如图12所示。可以看到仿真的4阶故障特征阶比及其倍频,验证了笔者提出的阶比峭度图算法对速度小范围波动的适应性和对不同加速度情况的适应性。
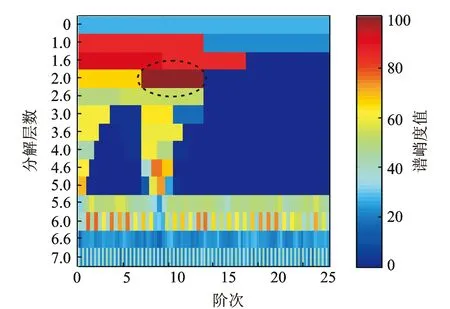
图11 仿真信号的阶比谱峭度图Fig.11 COT-kurtogram of the simulated signal
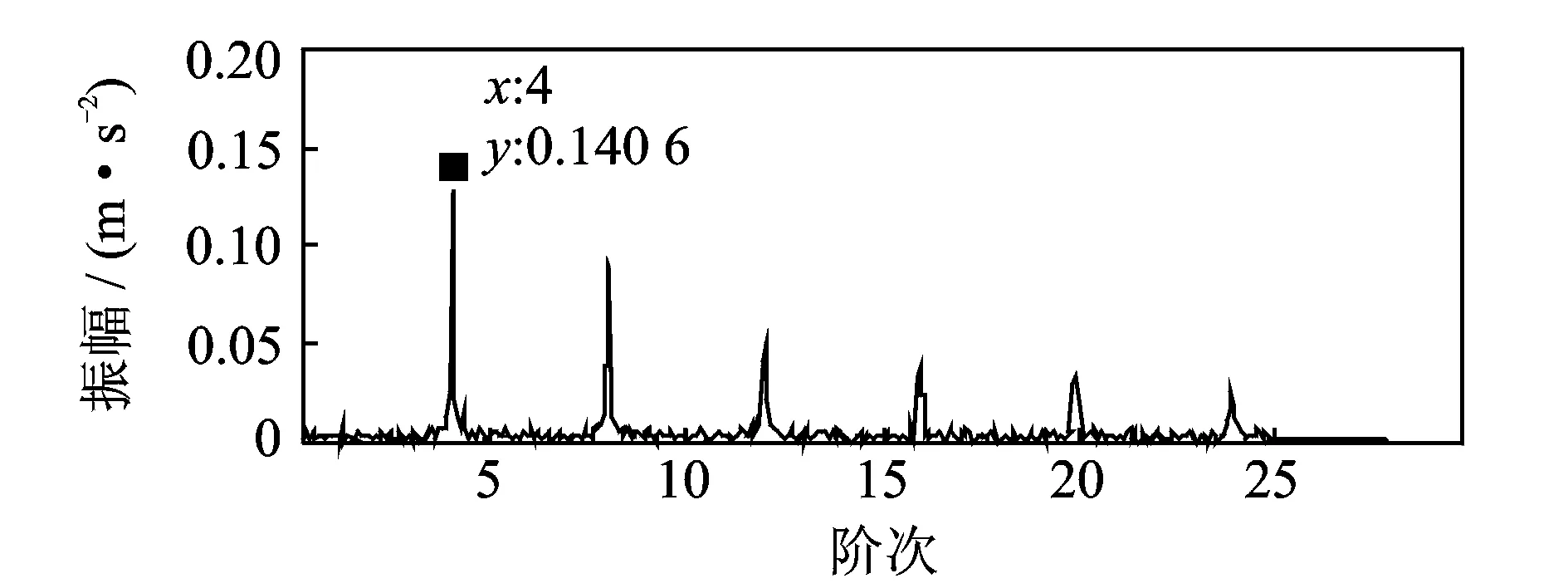
图12 仿真信号阶比谱Fig.12 Order spectrum of simulated signal
4 测试实验分析
为了验证阶比峭度图算法在实际滚动轴承故障特征提取中的优越性,笔者在滚动轴承振动实验平台上进行了验证。如图13所示,实验台采用直流并励电动机经半挠性联轴器直接驱动转轴,电机额定电流为2A,最大输出功率为250W。数据采集所用加速度传感器为美国CTC公司生产型号为M/WT135-1D的加速度传感器,采集点为故障轴承的支座上;转速传感器为SZGB-6型光电转速传感器。故障信号由五通道NI-USB4432采集卡采集得到。

图13 滚动轴承振动实验台Fig.13 Rolling bearing vibration test rig
故障轴承型号为HRB圆柱滚子轴承N205M,滚子个数为Z=13,滚子直径为d=7.5 mm,轴承节径为D=39.5 mm,轴承接触角α=0°。外圈故障特征阶比为
内圈故障特征阶比为
滚动体故障特征阶比为
保持架故障特征阶比为
设置采样率为20 kHz,选取实验过程中主轴转速从750 r/min加速到1 050 r/min的一段信号进行分析。图14为实测时域振动信号。图15为对应的主轴转速曲线。
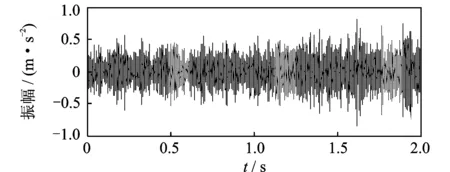
图14 实测滚动轴承外圈故障振动信号Fig.14 Tested rolling bearing outrace fault vibration signal
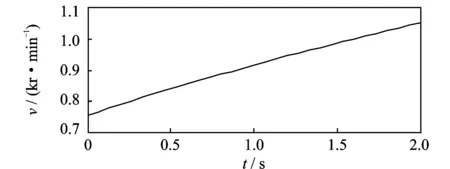
图15 转速信号Fig.15 Speed profile
对测试振动信号不进行阶比峭度图分析,只进行阶比跟踪得到的阶比谱,如图16所示。从图中找不到任何需要的轴承外圈故障特征阶比信息。
为了验证阶比峭度图算法的准确性,对信号根据图1流程进行传统峭度图分析,得到的峭度图如图17所示。可见,最优化解调频带出现在第2.5分解层上,解调中心频率为fc=9 166.7 Hz,带宽为bw=1 666.7 Hz(图中虚线框标示处)。
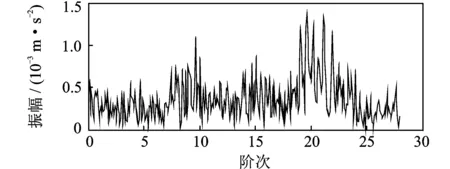
图16 实测振动信号阶比谱Fig.16 Order spectrum of the test signal without COT-kurtogram
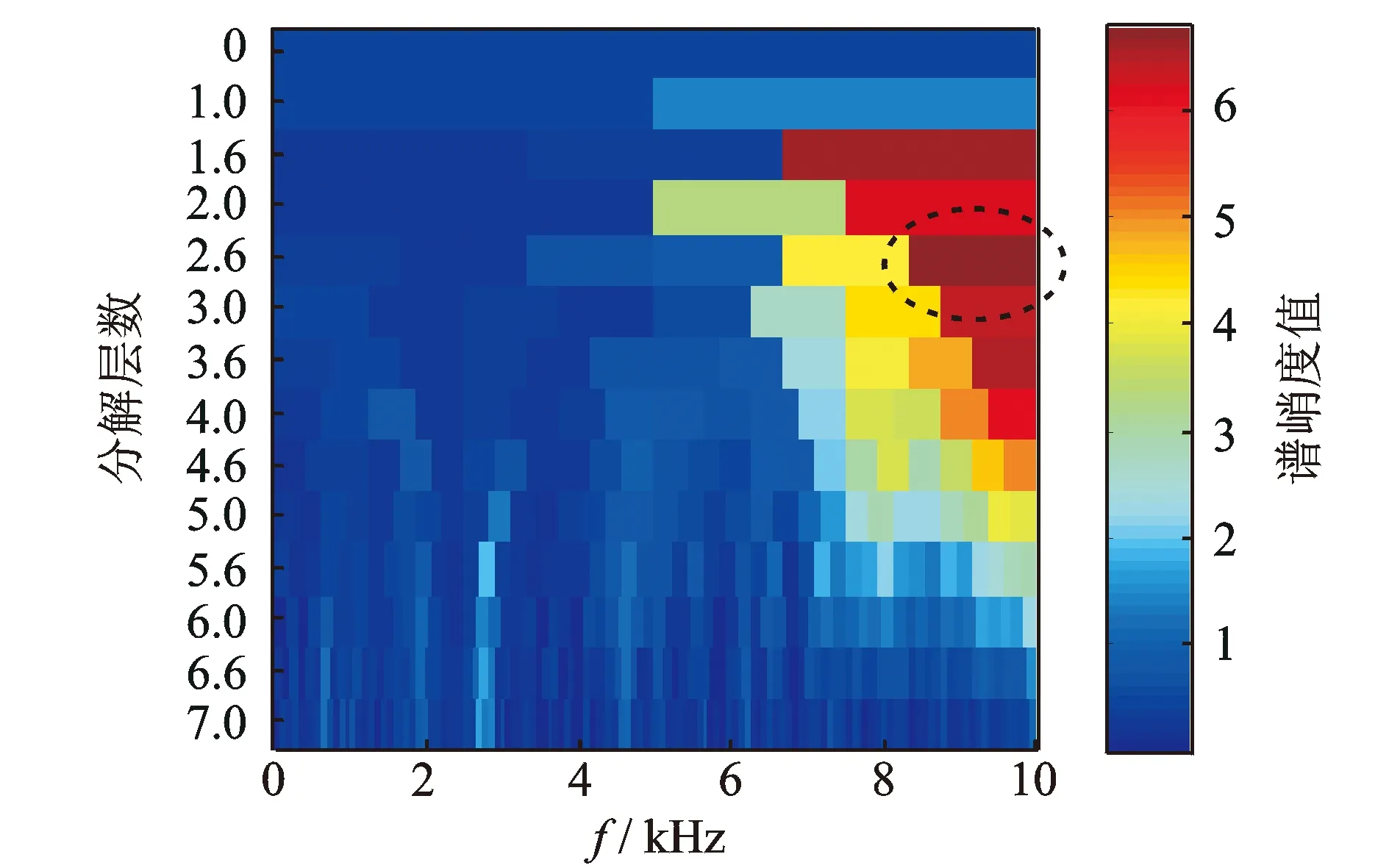
图17 实测信号的谱峭度图Fig.17 Kurtogram of practical signal
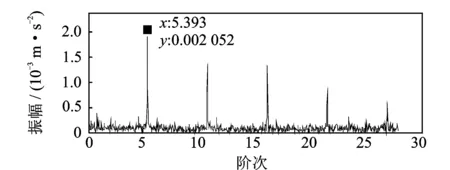
图18 实测振动信号传统谱峭度阶比谱Fig.18 Order spectrum of practical signal with traditional kurtogram
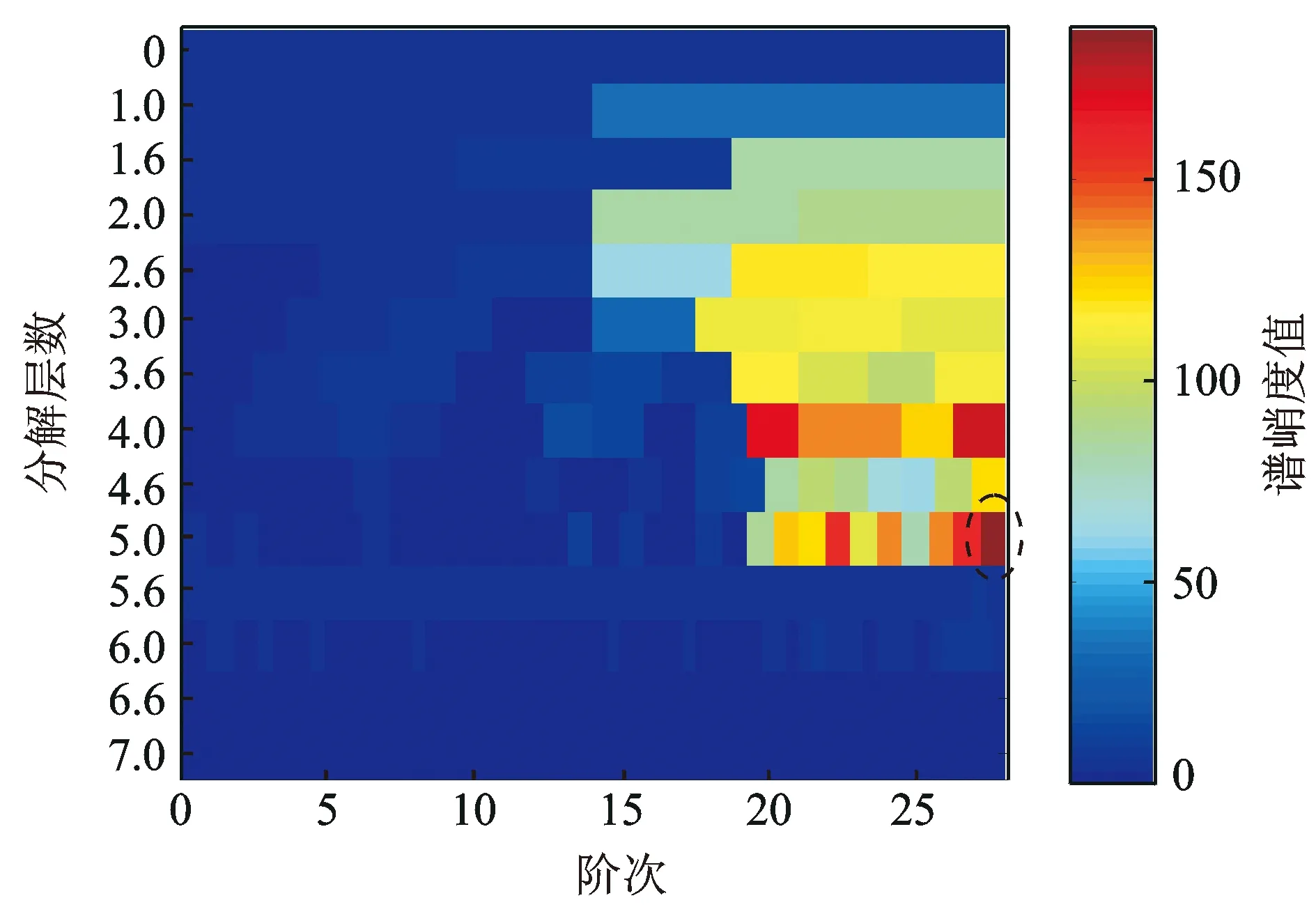
图19 实测信号的阶比峭度图Fig.19 COT-kurtogram of the test data
在最优解调频带处提取实测信号的优化包络时域信号进行等角度重采样,对应的阶比谱如图18所示。对实测振动信号进行阶比峭度图分析,得到的阶比峭度图如图19所示。可以看到,第5分解层上最大峭度SK1max=188.1处最优的解调中心阶比为Oc=27.56,阶比带宽为Bw=0.875(图中虚线框标示处)。在最优解调阶比带处提取实测信号的优化包络时域信号进行阶比等角度重采样,计算阶比谱如图20所示。
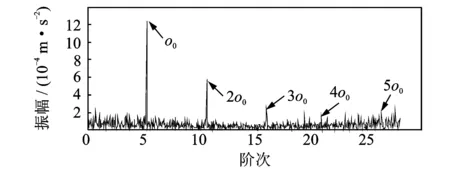
图20 实测振动信号阶比峭度阶比谱Fig.20 Order spectrum of the test signal with COT-kurtogram
相对于图16,从图20可以看到滚动轴承外圈故障特征阶比及其倍阶成分,与滚动轴承外圈故障的理论特征阶比及其倍频非常接近。表1为传统峭度图算法实测阶比(简写为传统实测)、阶比峭度图算法实测阶比(简写为阶比实测)与理论阶比值的对比及相对误差。一般滚动体和内外圈之间存在1~2%转频的滑动[11],传动误差和阶比分辨率也可能导致实测故障频率和理论故障频率存在一定误差。据此可判断滚动轴承外圈存在故障,且从表中得出阶比峭度图算法比传统峭度图算法的阶比准确性更高,进而证明了笔者提出的阶比峭度图算法在滚动轴承实际故障特征提取方面具有明显优势。
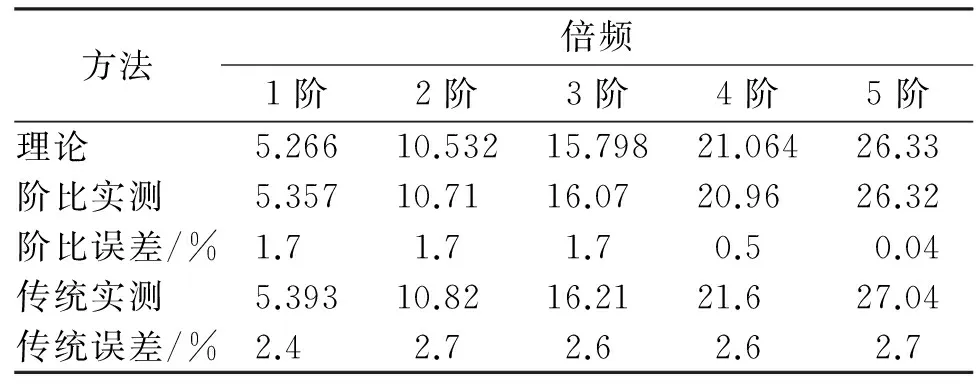
表1 实测阶比与理论阶比对比
5 结束语
融合计算阶比跟踪技术与峭度图方法,提出了适用于变转速下滚动轴承故障特征提取的阶比峭度图算法。该方法在阶比域平面内堆砌峭度图,进而确定最优解调阶比带参数及最优阶比谱。针对变转速下轴承故障振动信号的特征提取问题,该方法实现了直接在阶比域内的峭度图计算,相对于传统频域内峭度图计算,显著提高了峭度图计算的准确性。仿真及实测滚动轴承外圈故障信号分析结果均验证了该方法能够有效地将变速工况下的微弱轴承故障特征从低频干扰和强背景噪声中准确提取出来,具有良好的工程应用前景。
[1] 汤宝平,蒋永华,张祥春.基于形态奇异值分解和经验模态分解的滚动轴承特征提取方法[J]. 机械工程学报,2010,46(5):37-42.
Tang Baoping, Jiang Yonghua, Zhang Xiangchun. Feature extraction method of rolling bearing fault based on singular value decomposition-morphology filter and empirical mode decomposition[J]. Journal of Mechanical Engineering, 2010, 46(5):37-42. (in Chinese)
[2] Pearson K. Das fehlergesetz und seine verallgemeinerungen durch fechner und pearson[J]. A Rejoinder Biometrika, 1905, 4:169-212.
[3] Dyer D, Stewart R M. Detection of rolling element bearing damage by statistical vibration analysis[J]. ASME Transactions Journal of Mechanical Design, 1977, 100: 229-235.
[4] Dwyer R F. Detection of non-Gaussian signals by frequency domain kurtosis estimation[C]∥Proceedings of the International Conference on Acoustics, Speech, and Signal Processing. Boston: [s.n.], 1983: 607-610.[5] Antoni J. The spectral kurtosis: a useful tool for characterizing nonstationary signals[J]. Mechanical System and Signal Processing, 2006, 20: 282-307.
[6] 苏文胜. 滚动轴承振动信号处理及特征提取方法研究[D]. 大连:大连理工大学, 2010.
[7] Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21:108-124.
[8] 徐冠基, 柏林, 刘小峰, 等. 基于阶比分析的风力发电机噪声音调判定[J]. 振动、测试与诊断, 2010, 30(4): 451-454.
Xu Guanji, Bo Lin, Liu Xiaofeng, et al. Determination of the tonality of wind turbines acoustic noise based on order analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(4):451-454. (in Chinese)[9] 刘亭伟, 郭瑜. 基于谱峭度的滚动轴承故障包络阶比跟踪分析[J]. 振动与冲击, 2012, 31(17): 149-153.
Liu Tingwei, Guo Yu. Envelope order tracking analysis for rolling element bearing faults based on spectral kurtosis[J]. Journal of Vibration and Shock, 2012, 31(17): 149-153. (in Chinese)
[10]郭瑜, 秦树人, 梁玉前. 时频分析阶比跟踪技术[J]. 重庆大学学报:自然科学版, 2002, 25(5):17-20.
Guo Yu, Qin Shuren, Liang Yuqian. Order tracking method based on time-frequency analysis[J]. Journal of Chongqing University: Natural Science Edition, 2002, 25(5): 17-20. (in Chinese)
[11]Sawalhi N, Randall R B. Simulating gear and bearing interactions in the presence of faults part I. the combined gear bearing dynamic model and the simulation of localized bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1924-1951.

10.16450/j.cnki.issn.1004-6801.2016.04.007
国家自然科学基金资助项目(51475052);中央高校专项资金资助项目(106112016CDJZR115502)
2014-06-26;
2014-09-01
TH17; TP206
柏林,男,1972年11月生,教授、博士生导师。主要研究方向为虚拟仪器与信号处理。曾发表《Measurement system for wind turbines noises assessment based on LabVIEW》(《Measurement》2011,Vol. 44,No.2)等论文。
E-mail: bolin0001@aliyun.com
简介:甄杰,男,1989年5月生,硕士生。主要研究方向为机电一体化。
E-mail: happyzyj.love@163.com
